Ilan Fischer (2003)
Evolutionary Development and Learning: Two Facets of Strategy Generation
Journal of Artificial Societies and Social Simulation
vol. 6, no. 1
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/1/7.html>
Received: 7-Dec-2002 Published: 31-Jan-2003
 Abstract
Abstract

|
| (a) |

|
| (b) |
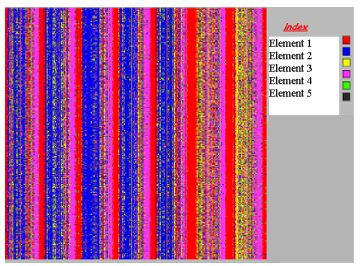
|
| (c) |
| Figure 1. Three stages in a Genetic Algorithm development: a - Initial random distribution; b - Partial convergence; c - A converged vector set |
| Table 1: A Prisoner's Dilemma Payoff Matrix | |||
| Player B | |||
| C | D | ||
| Player A | C | 5, 5 | -10, 10 |
| D | 10, -10 | -5, -5 | |
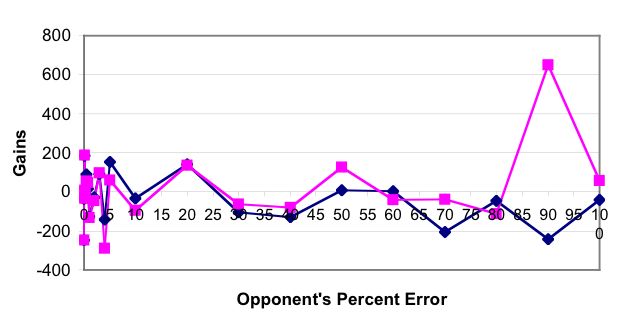
|
| Figure 2. Gains of a TFT playing agent with 30% errors (square), against TFT opponents with various error levels (diamond). |
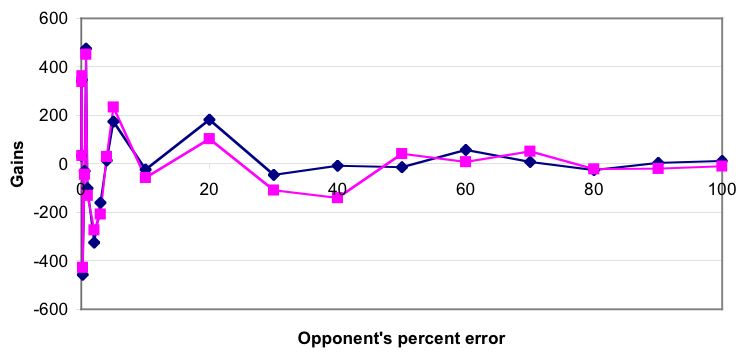
|
| Figure 3. Gains of a TFT playing agent with 5% errors (square) , against TFT opponents with various error levels (diamond). |
|
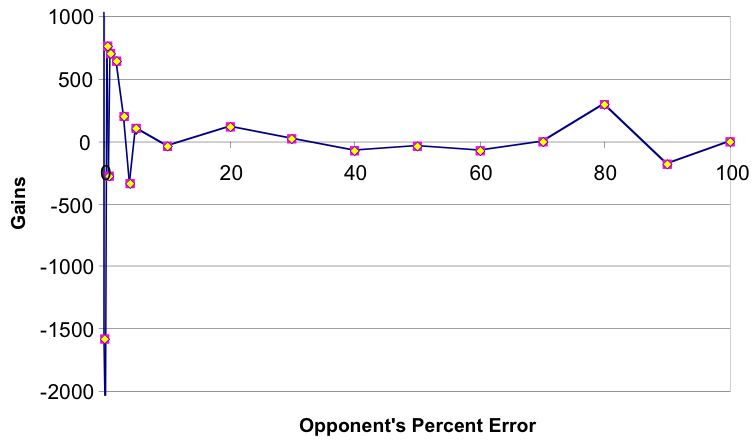
| Figure 4. Gains of a pure TFT agent (square), playing against TFT opponents with various error levels (triangle) |
AXELROD, R. (1980b). More effective choice in the Prisoner's Dilemma. Journal of Conflict Resolution, 24, 379-403.
AXELROD, R. (1981). The emergence of cooperation among egoists. The American Political Science Review, 75, 306-318.
AXELROD, R. (1984). The evolution of cooperation. New York: Basic Books.
AXELROD, R. (1997). Evolving new strategies: The evolution of strategies in the iterated Prisoner's Dilemma. In R. Axelrod (Ed.), The complexity of cooperation (pp. 41-29). New Jersey: Princeton University Press.
BENDOR, J. (1987). In good times and bad: Reciprocity in an uncertain world. American Journal of Political Science, 31, 531-538.
BENDOR,J., KRAMER, R. M., & STOUT, S. (1991). When in doubt: Cooperation in a noisy Prisoner's Dilemma. Journal of Conflict Resolution, 35, 691-719.
BUDESCU, D.V. (1987). A Markov model for generation of random binary sequences. Journal of Experimental Psychology: Human Perception and Performance, 13, 25-39.
CHATTOE, E. (1998). Just How (Un)realistic are Evolutionary Algorithms as Representations of Social Process? Journal of Artificial Societies and Social Simulation. 1, 3, <https://www.jasss.org/1/3/2.html>
FISCHER, I., & SULLIVAN, O. (in preparation). Evolutionary modeling of time-use vectors.
FUDENBERG, D., MASKIN, E. (1990). Evolution and cooperation in noisy repeated games. American Economic Review, 80, 274-279.
GILOVICH, T., VALLONE, R., & TVERSKY, A. (1985). The hot hand in basketball: On the misperception of random sequences. Cognitive Psychology, 17, 295-314.
GORRINII, V., & DORIGO, M., (1996). An application of evolutionary algorithms to the scheduling of robotic operations. In Alliot, J. M., Lutton, E., Ronald, E., and Schoenauer, M. (Eds.) Artificial Evolution. New York: Anchor Books
HOLLAND J. H. 1975. Adaption in Natural and Artificial Systems. University of Michigan Press, Ann Arbor, MI.
KAHNEMAN, D., & TVERSKY, A. (1972).Subjective probability: A judgment of representativeness. Cognitive Psychology, 3, 430-454.
KOLLOCK, P. (1993). An eye for an eye leaves everyone blind: Cooperation and accounting systems. American Sociological Review, 58, 768-786.
LAPLACE, P. -S. (1951), A philosophical essay on probabilities (F. W. Truscott & F. L. Emory, Trans.). New York: Dover. (original work published 1814).
SELTEN, R., (1975). Reexamination of the perfectness concept for equilibrium points in extensive games. International Journal of Game Theory, 4, 22-55.
WU, J., & AXELROD, R. (1997). Coping with noise: How to cope with noise in the Iterated Prisoner's Dilemma. In R. Axelrod (Ed.), The complexity of cooperation (pp. 41-29). New Jersey: Princeton University Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]