Derek Gatherer (2002)
Identifying cases of social contagion using memetic isolation: comparison of the dynamics of a multisociety simulation with an ethnographic data set
Journal of Artificial Societies and Social Simulation
vol. 5, no. 4
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/5/4/5.html>
Received: 21-Aug-2002 Accepted: 26-Oct-2002 Published: 31-Oct-2002
 Abstract
Abstract
|
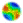
| Figure 1. Diagram of how the model works. Two memes are represented as red and blue attributes for agents, and two haploid genes as A and B. In panels A and B, societies with a majority of "red" memes are coloured orange, and societies with a majority of "blue" memes are pale blue. In panels C and D, societies with a majority of gene A are coloured grey, and those with a majority of gene B are coloured yellow. The gene and meme states of societies are designated according to the voting system described in Figure 2. In panel A, "reproduction over simple self-replacement" (white arrows), "teaching members of own society" (black arrows), "teaching members of neighbouring societies" (green arrows), and "migration" (blue arrows) occur. In panels B and C, the results of the events in panels A and C can be seen: as well as several individuals having changed their memes, some cells can be seen to have changed their designation (by the voting system) from one colour to another. Since a strictly vertically transmitted meme behaves exactly like a haploid gene, the model can simulate strictly vertical transmission and contagion, simultaneously. |
|
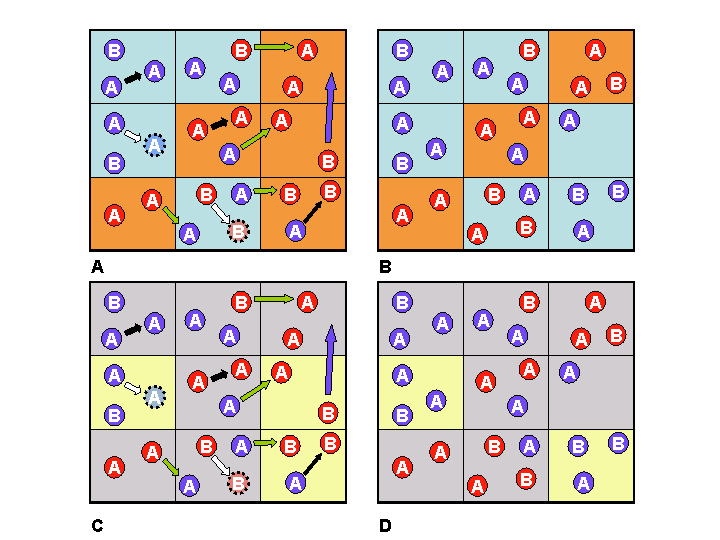
| Figure 2. First-Past-the-Post-Voting. Societies are coloured according to the majority of the agents within them (where numbers are even societies conservatively retain their original designation). Societies with no neighbouring society of the same designation are deemed to be memetic isolates. The grid above contains three blue memetic isolates and one red one. |
INITIALIZATION:
For each of the 100 cells in the 10-by-10 array:
{
place two Agents in each cell
randomly assign one of four Gene attributes to each individual
randomly assign one of four Meme attributes to each individual
}
ITERATION:
For 100 generations do the following:
{
For each Agent:
{
If Agent Meme attribute = "A" and CultSel = "Y"
{
Double parameters n and o for that agent
}
If Agent Meme attribute = "A" and NatSel = "Y"
{
Double parameter r for that agent
}
If a random number x < r
{
Reproduce Agent
}
If a different random number y < o
{
If same random number y is also < n
{
Transmit Meme to any Agent in any adjacent cell
}
else
{
Transmit Meme to any Agent in same cell
}
}
If a different random number z < m
{
Migrate Agent to adjacent cell
}
}
}
END.
|
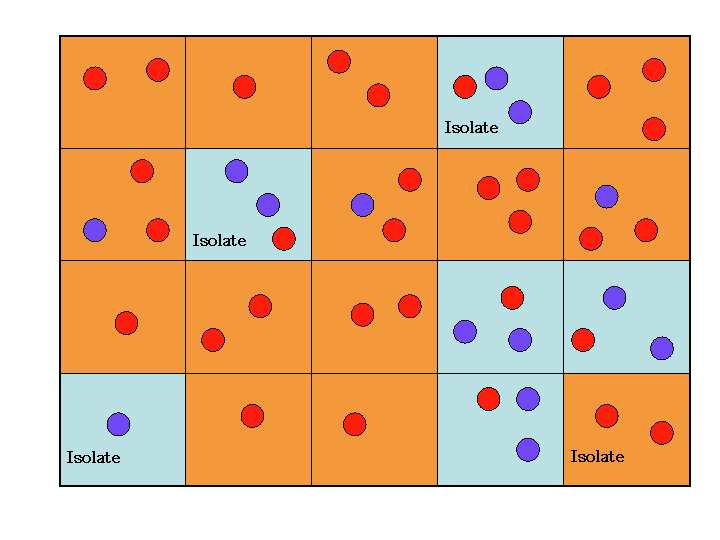
| Figure 3. Screenshots of three runs of Listing 1 after 100 generations. The upper panel shows the number of agents in each society/cell at the end of the 100 generations, the middle the frequency of Gene 1 and the lower the frequency of Meme A. Cells with a majority of Gene 1 or Meme A are coloured red. Those with a minority are green and those with none are coloured yellow. The figures for genetic isolation from left to right (second row) are, 2%, 1% and 5% respectively, and for cultural isolation (bottom row) are 3%, 1% and 0%. The right simulation had cultural selection operating on Meme A, resulting in its fixation. |
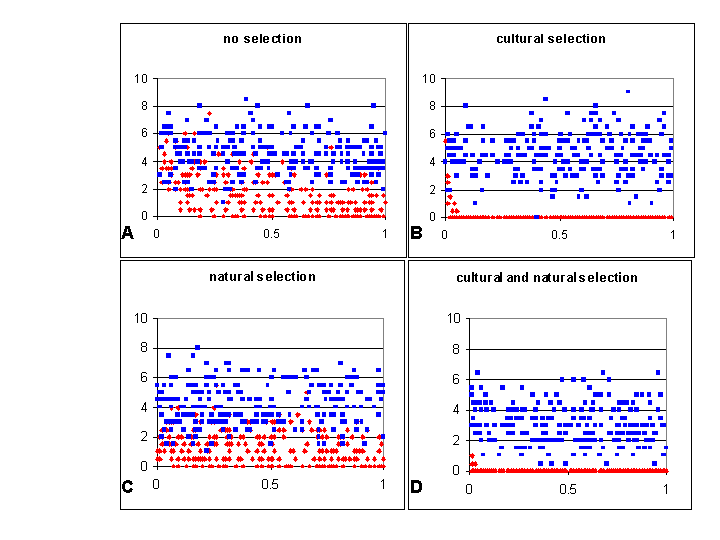
| Table 1: Mean percentage genetic and memetic isolation observed for 250 randomly initialised simulations (each simulation performed twice and results averaged), against the rate of teaching within societies, under the four conditions of no selective forces, natural selection alone, cultural selection alone or both. The individual values contributing to this summary are plotted graphically in Figure4. | |||
| Cultural Selection | Natural Selection | % genetic isolation | % memetic isolation |
| No | No | 4.53 | 1.61 |
| Yes | No | 4.54 | 0.07 |
| No | Yes | 4.24 | 1.22 |
| Yes | Yes | 3.06 | 0.01 |
|
| Figure 4. Percentage memetic isolation (red dots) and genetic isolation (blue dots) for 250 duplicated simulations, under each of the four selective conditions, plotted for convenience against the rate of teaching within societies (variable o in the model). Each data point is the average of two duplicate runs under the same randomly initialised m, n and o. Rate of overall reproduction (r in the model) was held at 0.01. This data is summarised in Table 1. |
| Table 2: Correlation co-efficients between the degree of memetic and genetic isolation and the three variable parameters of the simulation. Those correlations determined to be statistically significant at p < 0.01 using a t-test are highlighted in red. | ||||
| Cultural Selection | Natural Selection | Correlation with memetic isolation | Correlation with genetic isolation | Parameter |
| No | No | 0.12 -0.53 -0.18 | 0.10 -0.12 -0.01 | Migration Teach in own culture Teach neighbour |
| Yes | No | 0.06 -0.27 0.04 | 0.14 0.01 0.00 | Migration Teach in own culture Teach neighbour |
| No | Yes | 0.07 0.06 0.03 | 0.03 0.17 -0.10 | Migration Teach in own culture Teach neighbour |
| Yes | Yes | -0.10 -0.19 0.08 | 0.06 -0.10 0.06 | Migration Teach in own culture Teach neighbour |
|
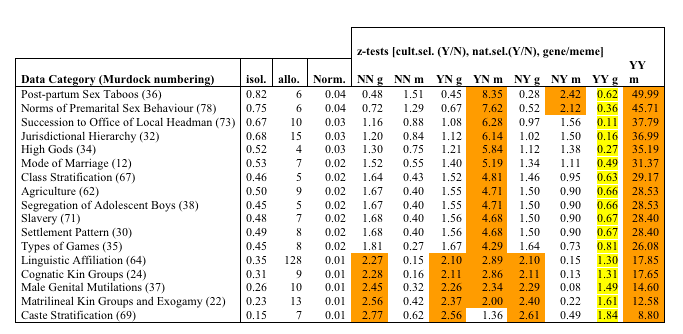
| Table 3. Summary of empirical data compared to simulations. |
|
The columns are as follows: Trait category: description and number taken from Murdock, isol.: average degree of memetic isolation for allomemes in that category, allo.: number of allomemes norm: the normalised memetic isolation against the random background, Z-tests: z-test comparing 8 models with the empirical data, cultural selection, natural selection and vertical or horizontal transmission, e.g. YN g = model of vertical trait where horizontal trait is under cultural selection; NY m = model of horizontal trait under natural selection etc. The orange shaded boxes are those where the z-test gives a value of > 1.96, thus indicating that the empirical data has p < 0.05 of conforming to the model. These are traits which are therefore unlikely to be explicable in terms of that model. The yellow stripe in column 7 indicates that this conformity to this simulation (drifting vertical trait, but with horizontal trait culturally and naturally selected in the same population) is improbable, although statistically possible (see text). |
|
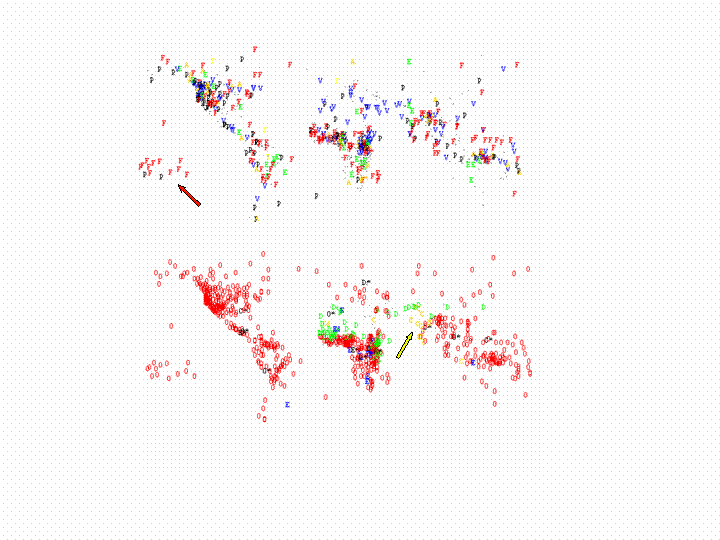
| Figure 5. Geographical distribution of cultural traits for two of Murdock's categories, chosen to contrast the upper and lower end of Table 3.. Above: "Norms of Premarital Sex Behaviour" (A: pregnancy avoidance, E: early marriage, F: "free love", T: trial marriage, P: weak prohibition, V: virginity). Below: "Caste Stratification" (C: complex, D: despised group, E: ethnic stratification, O: absent, dots are those societies for which no information is available in Murdock). Some well known features may be seen on the maps, such as Margaret Mead's focus of "free love" in the South Pacific (red arrow upper panel) and the presence of the caste system in the Indian subcontinent (yellow arrow lower panel). |
AXTELL, R., AXELROD, R., EPSTEIN, J.M. and COHEN, M.D. 1996. Aligning simulation models: a case study and results. Computational and Mathematical Organization Theory 1: 123-141.
BARBUJANI, G. and SOKAL, R.R. 1990. Zones of sharp genetic change in Europe are also linguistic boundaries. Proc. Natl. Acad. Sci. USA 87: 1816-1819.
CAVALLI-SFORZA, L.L. and FELDMAN, M.W. 1973. Models for cultural inheritance. I. Group mean and within group variation.. Theor Popul Biol. 4: 42-55.
CAVALLI-SFORZA, L.L. and FELDMAN, M.W. 1981. Cultural Transmission and Evolution. Princeton University Press, Princeton.
CAVALLI-SFORZA, L.L. 1979. Cultural change and its relevance for human genetics. Ciba Found. Symp. 66: 5-23.
CAVALLI-SFORZA, L.L., FELDMAN, M.W., CHEN, K.H. and DORNBUSCH, S.M. 1982. Theory and observation in cultural transmission. Science 218:19-27.
CASTELLANO, C., MARSILI, M. and VESPIGNANI, A. 2000. Nonequilibrium phase transition in a model for social influence. Physical Review Letters 85: 3536-3539.
DE SILVESTRI, A. and GUGLIELMINO, C.R. 2000. Ethnicity and malaria affect surname distribution in Consenza Province (Italy). Hum. Biol. 72: 573-83.
DURHAM, W.H. 1991. Coevolution: Genes, Culture and Human Diversity. Stanford University Press, Stanford.
FELDMAN, M.W. and CAVALLI-SFORZA, L.L. 1984. Cultural and biological evolutionary processes: gene-culture disequilibrium. Proc. Natl. Acad. Sci. USA 81:1604-1607.
GATHERER, D. 2002. The Spread of Irrational Behaviours by Contagion: An Agent Micro-Simulation. Journal of Memetics - Evolutionary Models of Information Transmission 6. http://jom-emit.cfpm.org/2002/vol6/gatherer_d.html
GONZALEZ JOSE, R., GARCIA-MORO, C., DAHINTEN, S. and HERNANDEZ, M. 2002. Origin of Fueguian-Patagonians: an approach to population history and structure using R matrix and matrix permutation methods. Am. J. Human Biol. 14: 308-320.
GRAY, R.D. and JORDAN, F.M. 2000. Language trees support the express-train sequence of Austronesian expansion. Nature 405: 1052-1055.
GUGLIELMINO, C.R., VIGANOTTI, C., HEWLETT, B. AND CAVALLI-SFORZA, L.L. 1995. Cultural variation in Africa: Role of mechanisms of transmission and adaptation. Proc. Natl. Acad. Sci. USA 92: 7585-7589.
KIMURA, M. (1979) The neutral theory of molecular evolution. Sci Am 241: 98-108.
KUMM, J., LALAND, K.N. and FELDMAN, M.W. 1994. Gene-culture coevolution and sex ratios: the effects of infanticide, sex-selective abortion, sex selection, and sex-biased parental investment on the evolution of sex ratios. Theor. Popul. Biol. 46: 249-278.
LALAND, K.N. 1994. Sexual selection with a culturally transmitted mating preference. Theor. Popul. Biol. 45: 1-15.
MURDOCK, G.P. 1967. Ethnographic Atlas. University of Pittsburgh Press, Pittsburgh.
RASHEVSKY, N. 1949. Mathematical biology of social behaviour I. Bull. Math. Biophys. 11: 105-113.
RENFREW, C. 1987. Archaeology & Language: The Puzzle of the Indo-European Origins. Jonathan Cape, London.
SIEVER, E., SPAINHOUR, S. and PATWARDHAN, N. (1998) Perl in a Nutshell. O'Reilly and Associates.
SOKAL, R.R., ODEN, N.L., LEGENDRE, P., FORTIN, M.J., KIM, J.Y. and VAUDOR, A. 1989. Genetic differences among language families in Europe. Am. J. Phys. Anthropol. 79: 489-502.
THOMSON, G. 1977. The effect of a selected locus on linked neutral loci. Genetics 85: 753-88.
UYENOYAMA, M., FELDMAN, M.W. and CAVALLI-SFORZA, L.L. 1979. Evolutionary effects of contagious and familial transmission. Proc. Natl. Acad. Sci. USA 76: 420-424.
VONA, G., CALO, C.M., LUCIA, G., MAMELI, G.E., SUCCA, V., ESTEBAN, E. and MORAL, P. 1996. Genetics, geography, and culture: the population of S. Pietro Island (Sardinia, Italy). Am. J. Phys. Anthropol. 100: 461-471.
WAGENER, D.K. and CAVALLI-SFORZA, L.L. 1975. Ethnic variation in genetic disease: possible roles of hitchhiking and epistasis. Am. J. Hum. Genet. 27: 348-364.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2002]