Reviewed by
Richard Holden
Centre
for Neural and Adaptive Systems, School of Computing, University
of Plymouth.

Wilson (chapter 1) introduces the idea that detailed simulations lead to analytical intractability and that, although detailed simulations are useful for biological realism, mathematical models can help in a kind of cyclical validation process; analytical models can complement simulations by providing a point of departure and simulations can give further insight, contributing to the process of model development. But how do we distinguish between a model and a simulation? Referring to ecosystems, J. Maynard Smith suggests a reasonably open ended definition and one we shall use to clarify the particular angle from which Wilson is trying to do his simulations:
"Whereas a good simulation should include as much detail as possible, a good model should include as little as possible" (Maynard Smith 1974)
An ecosystem, like any system is defined by a number of interacting parts. A simulation will capture the richness of these interactions in detail and a model will represent these interactions in the simplest way possible. The latter usually means a mathematical equation such as the following:
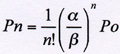
These symbols should then be described in terms of the particular interactions that they represent in the real world. This is indeed what qualifies as a model for Wilson although he never explicitly discusses the terms model and simulation.[1] Diplomatically, Wilson believes that the more models we have of a given system the better, perhaps because with a number of models general principles will reveal themselves. Wilson's 'simulations' tend towards the more simplistic end of the modelling-simulation spectrum; they don't include much detail.[2]
The book has two aims, to present the models and simulations while also introducing programming and the C programming language in order to achieve this. Given that most sole purpose introduction-to-programming-in-C type books are not very successful at introducing programming or C, it should not be expected that the programming advice given here would depart significantly from this standard. Indeed it doesn't. I will briefly comment on the programming parts of the book as I present its ecological content because this is how the book is itself arranged. There are no separate sections on programming, but the programs are embedded in the context of the subject matter on ecological systems. Hopefully by using this approach the reader will get a sense of organisational structure of the book. The main organisational thread throughout the book is the introduction of increasingly complex models and simulations.
Chapter two (Immigration-Emigration Models) introduces the reader to simple models of Immigration and Emigration in open systems. These models fall within the context of 'Queueing Theory' where simple models of queues allow members to join or leave a queue with a given probability so that the system is open to both growth and decay. Firstly, a deterministic model is presented and then the code is given. As the first section of the book, this chapter introduces the approach of presenting a mathematical model, implementing it and then presenting the results of an associated simulation. It is important to be aware of mathematical assumptions and also the effects of a particular implementation. Implementation leaves room for interpretation of a model and one could code a specific model in a number of ways. Usefully the book points out that although a simulation can free us from mathematical constraints, certain implementations will have their own characteristics and the output of simulations can reflect these.
The model is implemented in a compact form. As a supposed introduction to programming it might have been better to implement it in a more descriptive way. The author is not a computer scientist and has not been exposed to the important benefits of object-orientated design, but whatever language is used, it is important that the code is readable. The code is described in detail but not commented which sets a precedent throughout the book and does not help those new to programming (or C) to glance at a program and easily grasp its general meaning.
A stochastic model is then presented showing how an analytical model can capture these features of a simulation. The main lessons are that stochastic processes add formidable complexity to analytical models and results clearly demonstrate how the subtleties of implementation can affect the behaviour of the simulation markedly.
Closed population systems are the subject of chapter 3 (Logistic Birth-Death Models) where individuals enter or leave the system by birth and death. Such systems have their own internal logic and rates of change depend on internal conditions - simply population size here. A conceptually compressed (but mathematically neat) model of logistic population growth introduces this chapter. This constitutes a general model of deterministic logistic growth and describes many different systems. The general feature of such a model is its tendency to equilibrium. This is an important feature of closed systems and this equilibrium is approached regardless of initial population size.
The simulation model introduces some important programming concepts which are skipped over. The code is more substantial than the first simulation in the previous chapter and is explained while at the same time being rather self-consciously excused: "my emphasis is on getting a scientific result". The book claims to be an introduction to those seeking to adopt a computational approach to population dynamics and these defensive words do not instil the reader with confidence that they are learning good programming style. It should be mentioned that well written programs also produce a scientific result. A section on modelling concepts is thrown in at the end of this chapter. The section briefly mentions some important aspects of computational modelling and would perhaps benefit the reader by being placed at the beginning of the book before such details have already been introduced.
Chapter 4 (Random Numbers and Visualisation) introduces some further important features of the C programming language - in particular pointers. Single pointers to one dimensional arrays are covered and reasons given why passing pointers to functions is more efficient than passing by value. In the context of discussing pointers there is some confusion over the use of certain key terms used in C. The computational jargon is confused and, more worryingly, certain technicaldetails are simply incorrect. Those new to programming could easily become confused. I recommended that this book be read with a good introduction to the C programming language.
Information on the importance of avoiding bad random number generators is a useful diversion and very important in the simulation of complex systems. Some the problems associated with visualisation techniques are also mentioned and the use of some visuals to demonstrate a method of identifying bad random number generators is nice. Bad generators show patterns and this demonstrates well the difficulty of trying to make computers do things in an unstructured way. In the section on visualisation the concept of phase space is introduced briefly before .ps files. This chapter is a bit of a mixed bag of subjects and some of these subjects complement each other well while others leave you with the feeling of just having seen a fly in your soup. The models in this book do not present too much of a problem in terms of visualisation, but in more complex models where there can be many interacting elements and complex output, multidimensional visualisation can be very useful.[3]
Chapter 5 (Two Species Competition Model) introduces competition as an important factor in population dynamics using the trusty Lotka-Volterra competition model. Cellular models incorporating the concept of space are included and visualised as a march towards dominance of one species over another. An analytical model of the spatial simulation is provided, which might be of interest to those working with cellular automata type models whether for modelling ecological systems or not.
Projects exploring metapopulation dynamics and disease dynamics are presented as a means to exemplifying a small project life cycle in chapter 6 (Programming Projects). This may be useful for an undergraduate hoping to pursue research in the area of computational modelling. Ranges of simple and interesting projects are suggested from traffic dynamics to genetic drift. It is good that the techniques used in the book are shown to be useful across a range of areas and not only useful if confined to ecosystems models.[4]
Chapter 7 (Foraging Model) moves away from the population level of programming so far discussed and touches on the rule based behaviour of single individuals with specific goals in a given environment. Here population dynamics are related to the behaviour of individual elements in the system. Until this point in the book, individuals were treated as identical members of a species, constituting a homogenous collective. Opening up the possibility of modelling at an individualistic level allows us to produce populations as a heterogeneous collection of individuals. In Wilson's particular version of this approach cost based rules are very important and optimal behaviour is defined as finding minimum costs from a combination of behaviours. C's structure is introduced as a more advanced programming concept that allows the user to define the nature of the particular individuals and encapsulate it within a single data type.
Chapter 8 (Maintenance of Gynodioecy) presents a model of cohabitation where one species depends on the existence of another while also competing with it. The model involves the definition of how a stable equilibrium is achieved in such a system. Differential equations are used here and the Runge-Kutta technique is introduced as the standard computational algorithm for numerical integration. This simulation model is the most complex so far and the results show how a relatively simple mathematical model can capture the complexity of such a system very well even though the analytical description does not represent many aspects of reality.
The concept of space is often omitted in analytical ecosystem models. Chapter 9 (Diffusion and Reaction) attempts to provide a background to general concepts used in describing interactions within a spatially explicit ecological model. Spatio-temporal dynamics are investigated using linear stability analysis. The chapter slowly builds increasingly complex models and culminates in a predator prey model that allows for diffusing individuals. Diffusion equations allow this and the concepts are explained via a comparison of random walking individuals (as one form of diffusion process) with diffusion also being used to describe interaction between moving individuals with more 'purpose'. These models show a new set of phenomena that cannot be described by the simpler, non-spatial models. The classical Lotka-Voltera model is introduced and the sensitivity of these spatial models to stochastic detail is discussed well. This chapter includes some good references to other works.
In chapter 10 (Optimal Resource Allocation Schedules), the idea that schedules need to include allocation of resources to particular tasks over time is shown in the context of the life cycle of a plant. Allocation of resources to growth, maintenance and reproduction are not really separate interests (all contribute to fitness), but combinations of resources require particular types of allocation at different times. This can be very important to the overall reproductive success of a plant. Two types of allocation of resources to reproduction, continuous allocation and allocation in larger quantities (but in discrete packages) are considered. This enables a comparison to be made. We can see how a different strategy will contribute to fitness in a different way and how fitness is itself a dynamic concept. The concept of constrained optimisation is introduced where engineering meets biology and fitness is definable as mathematical function optimisation. Optimal allocations are derived from a mathematical perspective before the chapter introduces a population-based approach (the Genetic Algorithm). Genetic Algorithms are widely used in resource allocation and scheduling type problems and again here we see how there are shared interests between seemingly unrelated fields of research.
The Genetic Algorithm is introduced in its traditional form without any mention of how not only Evolutionary Algorithms (EA) but other search algorithms and techniques have been used to model a wide variety of processes in nature and contribute to the development of theoretical biology. It seems ironic in a book about evolutionary and ecological systems written by a biologist that the EA community is only represented as seeking to optimise solutions.[5]
Evolutionary and Ecological Systems in C is a brave attempt to teach programming (and C) to people already familiar with computational modelling techniques. The book is very worthwhile as there aren't many books around on this subject which make use of a technical language. Although the programming advice given is second rate, to see a mathematical model and then a full implementation of that model with a detailed description of the code is still useful. This approach opens up mathematics to the computer programmer and programming to those who are more familiar with the mathematics. I think the book might have benefited either by including more detail on programming concepts at the expense of a few models. Alternatively, it could have struck out the goal of introducing programming and recommended a few good reference books on C instead. There is probably enough programming information in Wilson's book when combined with such a reference.[6] The problem isn't the inclusion of code, but the forcing of technical details into spaces too small. The book suffers from being the result of a semester course on Ecological Modelling and issues that do need first hand teaching are crammed into the book. The book in parts is difficult to understand because of this, but the reader will get outof the book what they put in and in this respect some hard work may well pay off. Also this is an opportunity for the social scientist to get to grips with some mathematical techniques that may come in useful; ecological modelling is not just important for biologists, but is a well worth tool for social science simulators to own and the modelling/C style of this book offers a 'way in' for those without a mathematical background.
1 For a good discussion of models and simulations see chapter 4 of Noble (1998).
2 This is not a criticism. Many ecosystem models now contain a large amount of detail. In comparison, Wilson's 'simulations' are relatively simplistic, but this does not mean that detailed models are good and simple models are bad. Different models are used for different things.
3 Multidimensional Visualisation will become an important research area as computers allow the implementation of increasingly complex algorithms. This is an active field of research, see Spears (1999).
4 Evolutionary and ecosystem software can be applied across a range of areas in both academia and industry, see Bonsma et al. (2000).
5 See Miller (1994) for a more radical view of simulation techniques which might be used in biology.
6 Kernighan and Ritchie (1988) is a good example of such a reference.
BONSMA E., M. Shackleton and R. Shipman 2000. Eos: An evolutionary and ecosystem research platform. BT Technology Journal, 18:24-31.
KERNIGHAN B. W. and D. M. Ritchie 1988. The C Programming Language, second edition. Prentice-Hall, Englewood Cliffs, NJ.
MAYNARD SMITH J. 1974. Models in Ecology. Cambridge University Press, Cambridge.
MILLER G. E. 1994. Artificial life as theoretical biology: How to do real science with computer simulation. Cognitive Science Research Paper 378, School of Cognitive and Computing Sciences, University of Sussex.
NOBLE J. 1998. The Evolution of Animal Communication Systems: Questions of Function Examined Through Simulation. PhD Thesis, University of Sussex.
SPEARS W. M. 1999. 'An Overview of Multidimensional Visualisation Techniques', in Wolfgang Banzhaf, Jason Daida, Agoston E. Eiben, Max H. Garzon, Vasant Honavar, Mark Jakiela and Robert E. Smith, editors, GECCO-99: Proceedings of the Genetic and Evolutionary Computation Conference, Morgan Kauffman, San Francisco, CA.
Return to Contents
of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 2002