C. van Dijkum, J. van Mens-Verhulst, E. van Kuijk and N. Lam (2002)
System Dynamic Experiments with Non-linearity and a Rate of Learning:
the development of chronic fatigue complaints
Journal of Artificial Societies and Social Simulation
vol. 5, no. 3
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/5/3/6.html>
Received: 24-Mar-2002 Accepted: 12-Jun-2002 Published: 30-Jun-2002
 Abstract
Abstract
|
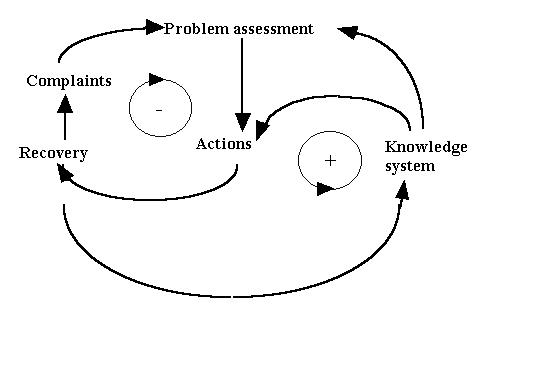
| Figure 1. The basic causal diagram of our self-regulation model |

|
| Table 1. An excerpt from a diary |
|
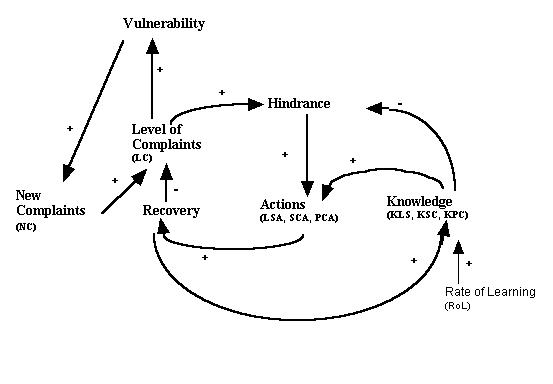
| Figure 2. An extended causal diagram of the variables used in our model |
|
|
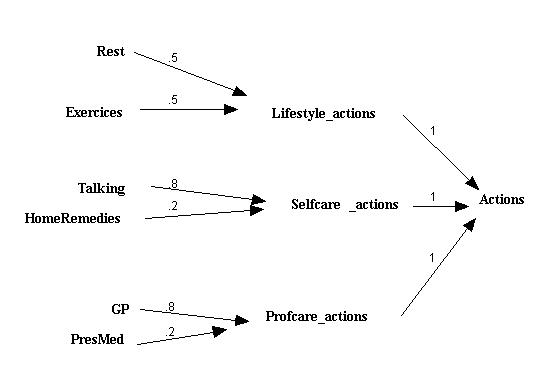
Figure 3. The action variables and their relative strengths Numbers stand for weighting coefficients |
Equation 1
Rest = if Knowledge_Lifestyle=0 then round(.6*Hindrance_complaint)
else round( .6*Hindrance_complaint*Knowledge_Lifestyle)
Rest = if .4* Hindrance>=.5 then 1
else 0
However, it was assumed that the decision underlying the action will be influenced by the knowledge that someone has of its effects. Past success should increase the chance of it being re-used. This assumption has been modelled in an embedded 'if', by using the knowledge variables (KLA, KSC or KPC) as multiplier. An example of such an equation is:
Equation 2
Rest = if Knowledge_Lifestyle=0 then round(.6*Hindrance_complaint)
else round( .6*Hindrance_complaint*Knowledge_Lifestyle)
Equation 3
ΔLevel_of_complaints/Δt = New_complaints - Recovery
Equation 4
New_complaint=round[random(o,maximum*vulnerability]
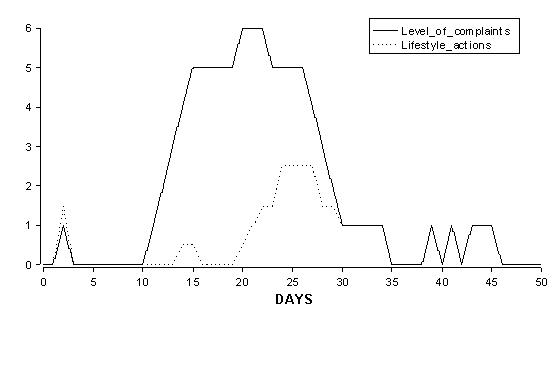
|
| Figure 4. The changes in one individual of levels of complaint (LC) and lifestyle_actions (LSA) over a period of 50 days |
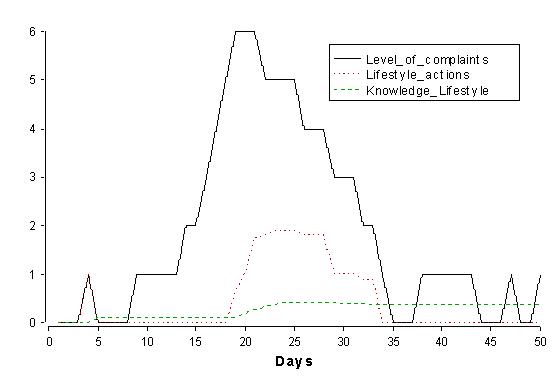
|
| Figure 5. Changes in complaint levels (LC), Lifestyle_actions and Knowledge_Lifestyle for one individual over a period of 50 days |
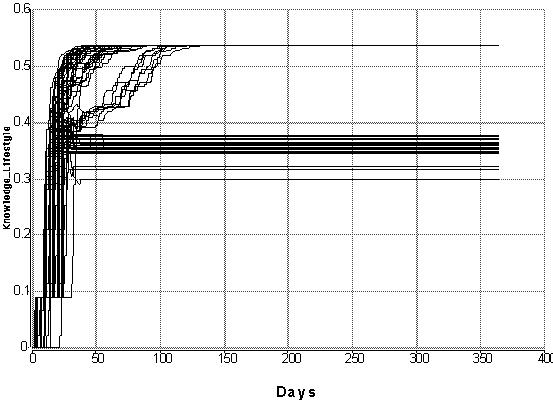
|
| Figure 6. The 'Development of Knowledge' life style (KLS) of 100 individuals with a constant rate of learning of 0.25, for a period of a year |
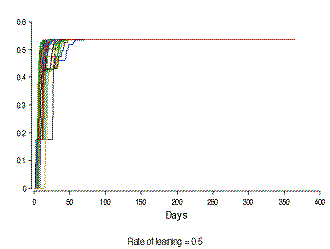
| 
|
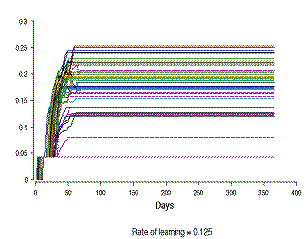
| 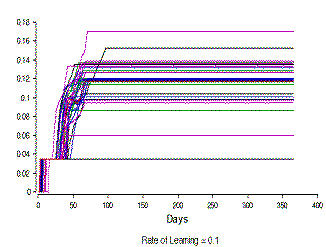 |
|
Figure 7. The development in the level of knowledge about life-style (KLS) in a hundred people with different rates of learning (The Y-axis differs in scale) | |
Vulnerability = Level_of_complaintsHowever, independent of the 'Level_of_Complaints', the maximum vulnerability will be 1 at the most. That means that - when vulnerability approaches the maximum of 1- the amount by which vulnerability is increased has to be near zero, also if the variable 'Level_of_Complaints' is very large. A simple mathematical expression which expresses this is:
Vulnerability = 1 - 1 / Level_of_complaintsThis equation should imply that vulnerability will be at a minimum when the Level_of_complaints is zero. To achieve this, one has to amend the reciprocal relation into:
Vulnerability = 1 - 1 / (Level_of_complaints + x)with such value of x that Vulnerability = 1 when Level_of_complaints = 0. The most simple equation which will be according these conditions is:
Vulnerability = 1-(1/(2+Level_of_complaints))Combined with the equations:
Chance_on_Complaint=round(Random_complaints*Vulnerability)and
Random_complaints = RANDOM(0,1.5)it at last leads to the difference equation:
ΔLevel_of_complaints / Δt = ROUND[RANDOM(0, 15) * (1 - (1 / (2 + Level_of_complaints))]
(Time in days; dt is one day)
Level_of_complaints(t) = Level_of_complaints(t-dt) + (New_complaints - Recovery) * dt
INIT Level_of_complaints = 0
New_complaints = Chance_on_a_Complaint
Recovery =
if Level_of_complaints=0 then 0
else
if round(Profcare_actions+Selfcare_actions+Lifestyle_actions)>=1 then 1
else 0
Chance_on_a_Complaint = round(Random_complaints*Vulnerability)
Random_complaints = RANDOM(0,1.5)
Vulnerability = 1-(1/(2+Level_of_complaints))
Knowledge_Lifestyle(t) = Knowledge_Lifestyle(t - dt) + (Lifestyle_learning) * dt
INIT Knowledge_Lifestyle = 0
Lifestyle_learning =
if Total_response=0 then 0
else if Lifestyle_actions=0 then 0
else ((Lifestyle_actions/Total_response*Recovery -Knowledge_Lifestyle)/Rate_of_learning)
Knowledge_Profcare(t) = Knowledge_Profcare(t - dt) + (Profcare_learning) * dt
INIT Knowledge_Profcare = 0
Profcare_learning =
if Total_response=0 then 0
else if Profcare_actions=0 then 0
else ((Profcare_actions/Total_response*Recovery)-Knowledge_Profcare)Rate_of_learning)
Knowledge_Selfcare(t) = Knowledge_Selfcare(t - dt) + (Selfcare_learning) * dt
INIT Knowledge_Selfcare = 0
Selfcare_learning =
if Total_response=0 then 0
else if Selfcare_actions=0 then 0
else ((Selfcare_actions/Total_response*Recovery)-Knowledge_Selfcare)/Rate_of_learning
Rate_of_learning = 1
Hindrance_complaint =
if Knowledge_actions=0 then (Level_of_complaints*(1+Worry_complaint))*(2-Reason_complaint)
else (Level_of_complaints*(1+Worry_complaint))*(1+Knowledge_actions)*(1+Reason_complaint)
Knowledge_actions = (Knowledge_Lifestyle+Knowledge_Profcare+Knowledge_Selfcare) / 3
Reason_complaint = .4
Worry_complaint = .6
Rest =
if Knowledge_Lifestyle=0 then round(.6*Hindrance_complaint)
else round( .6*Hindrance_complaint*Knowledge_Lifestyle)
Exercices =
if Knowledge_Lifestyle=0 then round(.4*Hindrance_complaint)
else round( .4*Hindrance_complaint*Knowledge_Lifestyle)
Lifestyle_actions =(.5*Rest+.5*Exercices)
Talking =
if Knowledge_Selfcare=0 then round( .5*Hindrance_complaint)
else round(.5*Hindrance_complaint*Knowledge_Selfcare)
HomeRemedies =
if Knowledge_Selfcare=0 then round(.3*Hindrance_complaint)
else round(.3*Hindrance_complaint*Knowledge_Selfcare)
Selfcare_actions = (.8*Talking+.2*HomeRemedies)
GP =
if Knowledge_Profcare=0 then round(.2*Hindrance_complaint)
else round( .2*Hindrance_complaint*Knowledge_Profcare)
PresMed =
if Knowledge_Profcare=0 then round(.5*Hindrance_complaint)
else round(.5*Hindrance_complaint*Knowledge_Profcare e)
Profcare_actions = (.8*GP+.2*PresMed)
Total_response = Lifestyle_actions+Profcare_actions+Selfcare_actions
2 Its theoretical maximum equals the number of simulated days.
3 Analytically viewed, it is easier to work with differential equations. However, with computer simulation, one works with difference equations, because computers have to operate with finite time steps.
4 Actually, the weights of the variables are inferred from unstandarized (linear regression) Betas of variables that discriminated between successes and failures of actions. The Betas were re-scaled for the clusters of (always positively interpreted) variables mentioned. The simulation model itself did not appear to be very sensitive to variation in these values.
5 The number 100 is quite arbitrary. It could also be 105. It is important, however, that the number is large enough to produce a qualitative interpretable pattern in the outcome, but not so large that it would take too much computer time. In any cae, the qualitative pattern of outcome is not sensitive to variations in the range of 100.
6 Prigogine (1980: 132) stated that in a critical region - near bifurcation - stochastic fluctuations drive the average. However, the pattern of the outcome has to be explained from the deterministic (internal) dynamics of the non-linear differential equations (e.g. p. 150). We are still exploring the intriguing combination of stochastic fluctuations and non-linear feedback cycles (see also Prigogine, pp. 123-127) to enable us to position our argument within the ongoing discussion about the relation between 'deterministic chaos' and 'stochastic fluctuation' (see also: Berliner 1992)
BISHOP, G.D. (1987). Lay conceptions of physical symptoms. Journal of Applied Social Psychology 17: 127 - 146.
DIJKUM C. van (1998). The validation of simulation models. In: E. Kerkhoffs and A. Bargiela (Eds.). Simulation Technology:Science and Art. Nottingham: Society of computer simulation, 221-224.
DIJKUM C. van, Tombe D. de, Kuijk E. van (Eds.) (1998). Validation of Simulation Models. Amsterdam: Siswo.
DIJKUM C van, and LANDSHEER H. (2000). Experimenting with a non-linear dynamic model of juvenile criminal behavior. Simulation & Gaming 31/4: 479-490.
DIJKUM C. van, LAM N., and GANZEBOOM H. (2001). The dynamics of educational expansion: A simulation model. In: F. Geyer and H. Zouwen van der (Eds). Sociocybernetics: Complexity, Autopoiesis, and Observation of Social Systems. (pp. 205-222). Westport: Greenwood Publishers.
FORRESTER J. (1968). Principles of Systems. Cambridge: Wright Allen Press.
HAEFNER J. W. (1996). Modeling Biological Systems: Principles and Applications. New York: Chapman & Hall.
LEVENTHAL, H. , MEYER, D. and NERENZ, D. (1980). The commonsense representation of illness danger. In: S. Rachman (ed), Medical Psychology, Vol.2: 2-30. New York: Pergamon.
LEVENTHAL, H., NERENZ, D. and STEELE, D.J. (1984). Illness Representations and Coping with Health Threats. In: A. Baum, S.E. Taylor and J.E. Singer (Eds.). Handbook of Psychology and Health, Vol. 4: 219-252. N.J.: ER/Baum,
LEVENTHAL, H. LEVENTHAL, E.A. and SCHAEFER, P.M. (1990) Vigilant coping and health behavior. In: M. Ory and R. Abeles (Eds.) Aging, Health and Behavior, pp.109-140. Baltimore: The John Hopkins Press.
LEVENTHAL, H. and DIEFENBACH, M. (1991). The active side of illness cognition. In: J.A. Skelton and R.T. Croyle (Eds.). Mental Representation in Health and Illness, pp.247-272. New York: Springer.
LEVENTHAL. H. LEVENTHAL, E.A. and CONTRADA, R. (1998) Self-regulation, health and behavior: A perceptual-cognitive approach. Psychology & Health 13/4: 717-735.
LISDONK, E.H. van de (1985) Ervaren en aangeboden morbiditeit in de huisartspraktijk. Thesis. Nijmegen, KUN
MENS-VERHULST, J. van and BENSING, J.M. (1998). Distinguishing between chronic and non-chronic fatigue, the role of gender and age. Social Science and Medicine 47/5: 621-634.
MENS-VERHULST, J. van, DIJKUM, C, van, KUIJK, E. van and LAM, N. (1999) . Dealing with fatigue: The importance of health-related action patterns. Patient Education and Counseling 36: 65-74.
PRIGOGINE I. (1980). From Being to Becoming. Time and Complexity in the Physical Sciences. New York: Freeman.
RICHARDSON G.P. and PUGH III, A.P. (Eds.)(1981) Introduction to System Dynamics Modeling. Cambridge MA: MIT Press.
RIJK,A. (1999). Fatigue in General-Practice Patients. An empirical study of fatigue in general practice and the development of the Quality-Quantity model for understanding fatigue. Thesis. Utrecht University.
SHARPE, M. and BASS, C. (1992). Pathophysiologica; mechanisms in somatization. International Review of Psychiatry 4: 81-97.
VERHULST F. (1990). Nonlinear differential equations and dynamical systems. Berlin: Springer Verlag.
WESSELY, S. and NIMNUAN, C. (1999). Functional somatic syndromes: one or many? Lancet 354/ 9182: 936-939.
ZOUWEN H. van der , DIJKUM C. van (2001). Towards a methodology for the empirical testing of complex social models. In: H. van der Zouwen and F. Geyer (eds.), Sociocybernetcs: Complexity, Autopoisis, and Observation of Social Systems, pp. 223-240. Westport: Greenwood Publishing Group.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2002]