R. Bagni, R. Berchi and P. Cariello (2002)
A comparison of simulation models applied to epidemics
Journal of Artificial Societies and Social Simulation
vol. 5, no. 3
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/5/3/5.html>
Received: 30-Sep-2001 Accepted: 5-Jun-2002 Published: 30-Jun-2002
 Abstract
Abstract
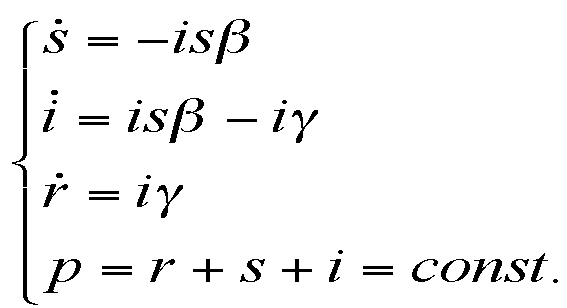
|
where the meanings of parameters are:
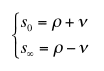 |
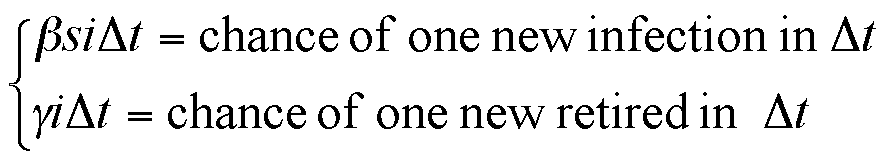
|
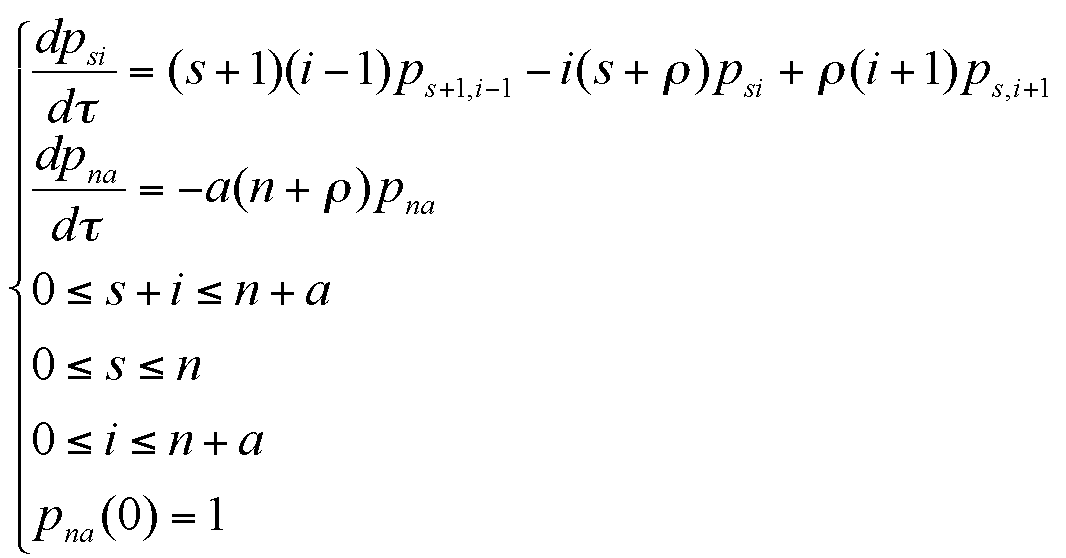
|
St = It+1 + St+1
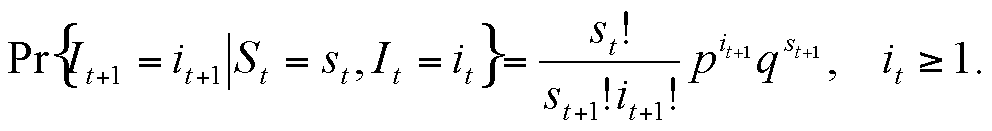
|
This can be rewritten in a form that depends only on the susceptible variable, so that we obtain a univariate Markov chain expression:
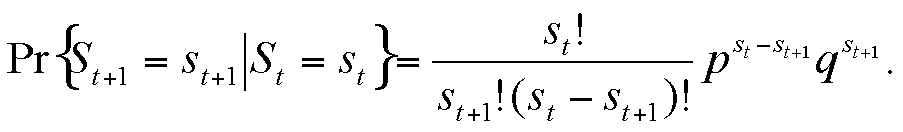
|
|
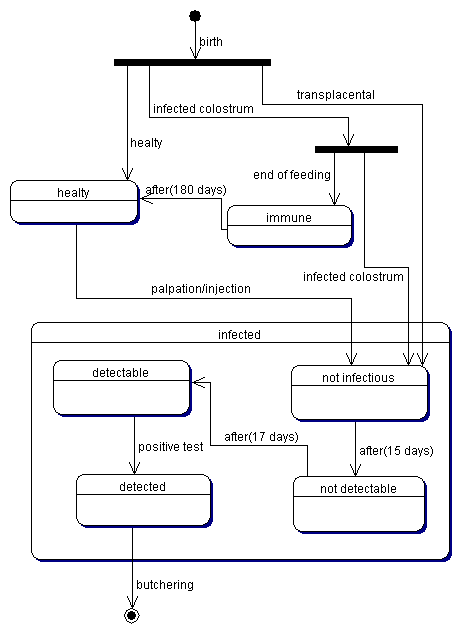
| Figure 1. The contagion process |
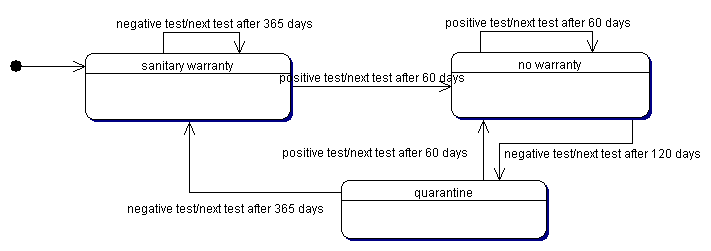
|
| Figure 2. The current control policy |
|
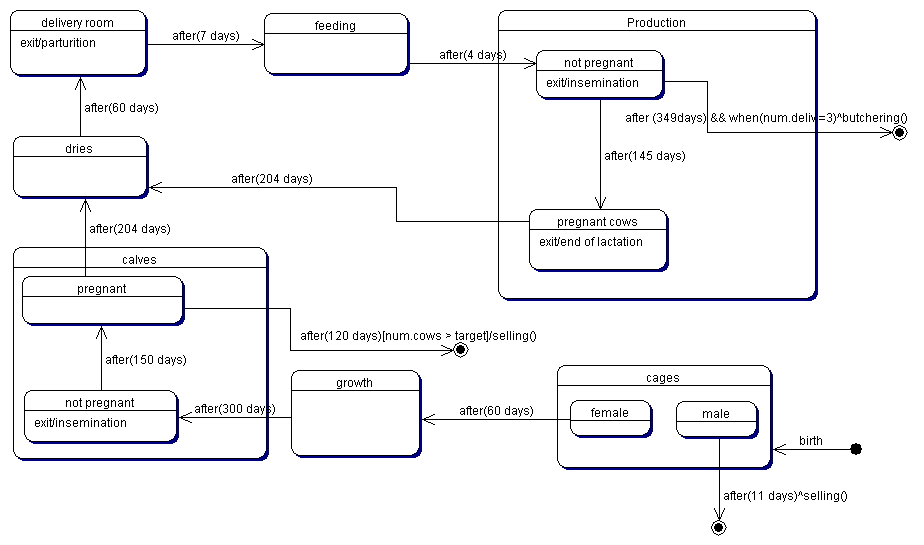
| Figure 3. The typical life cycle of a cow |
|
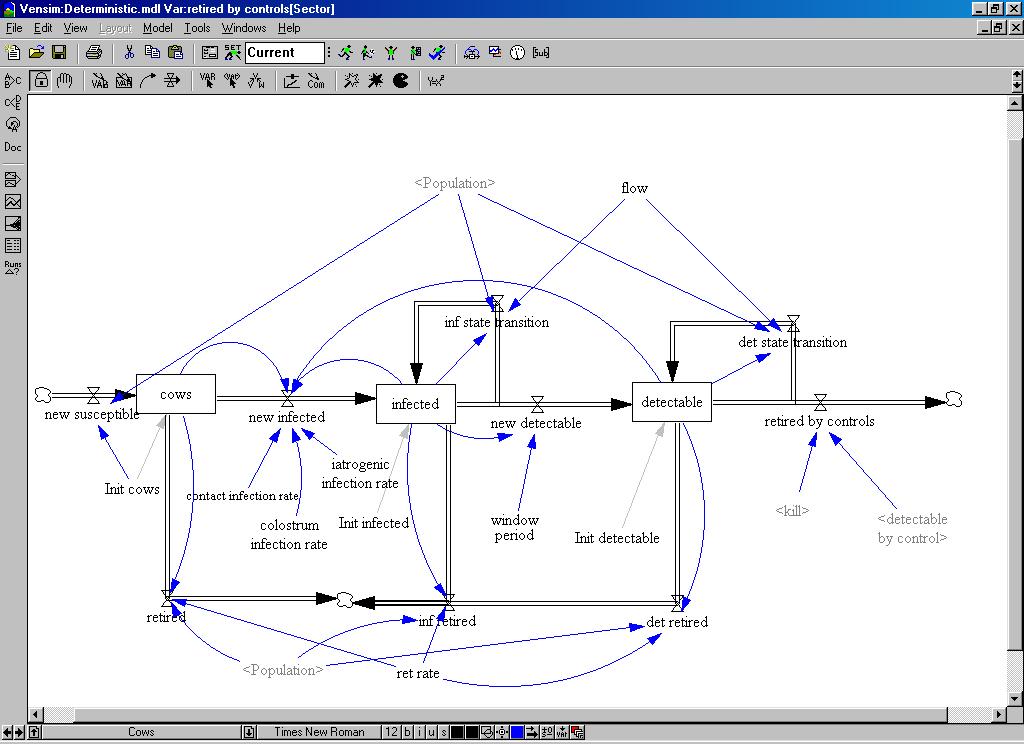
| Figure 4. The structural diagram of the system dynamics model |
|
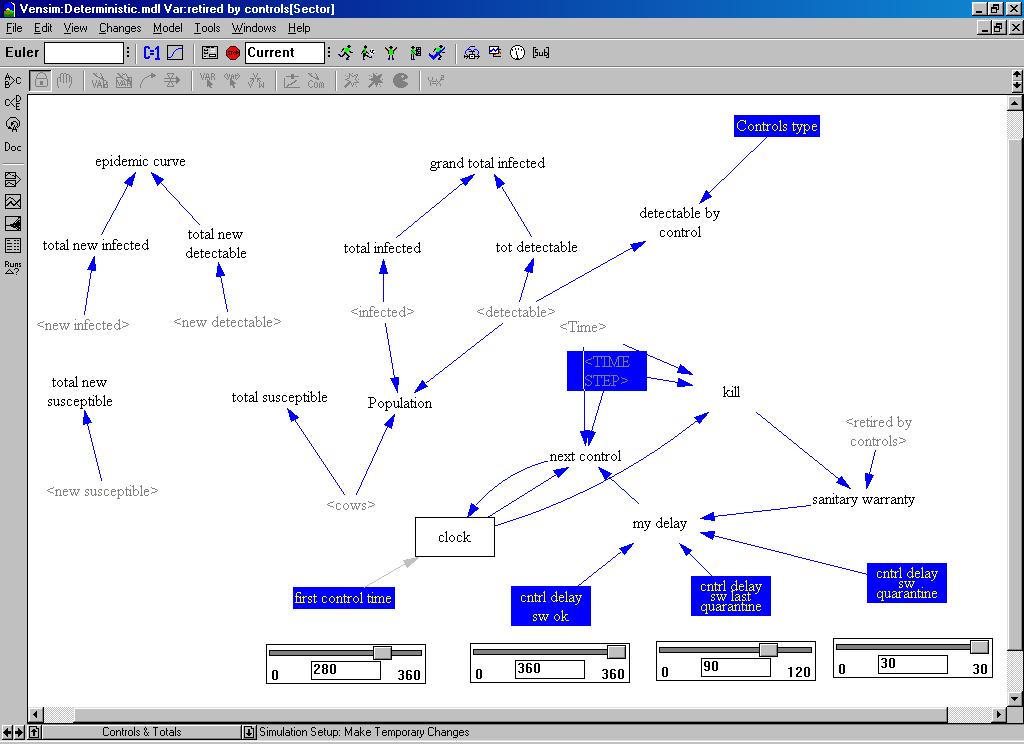
| Figure 5. The controls and totals in the system dynamics model |
|
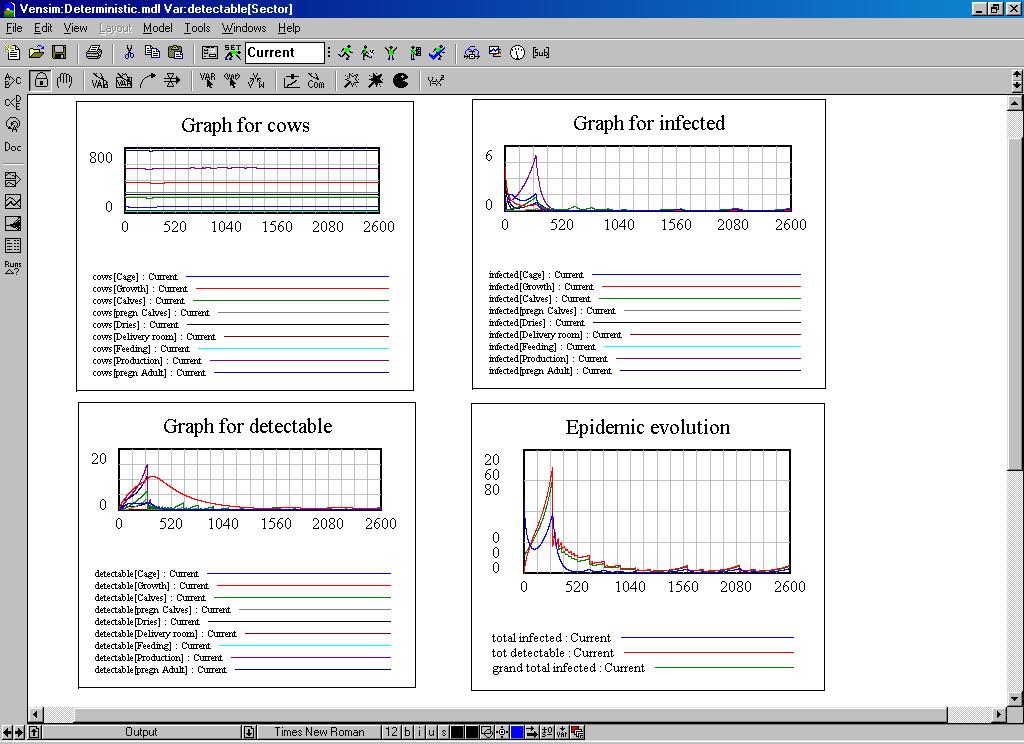
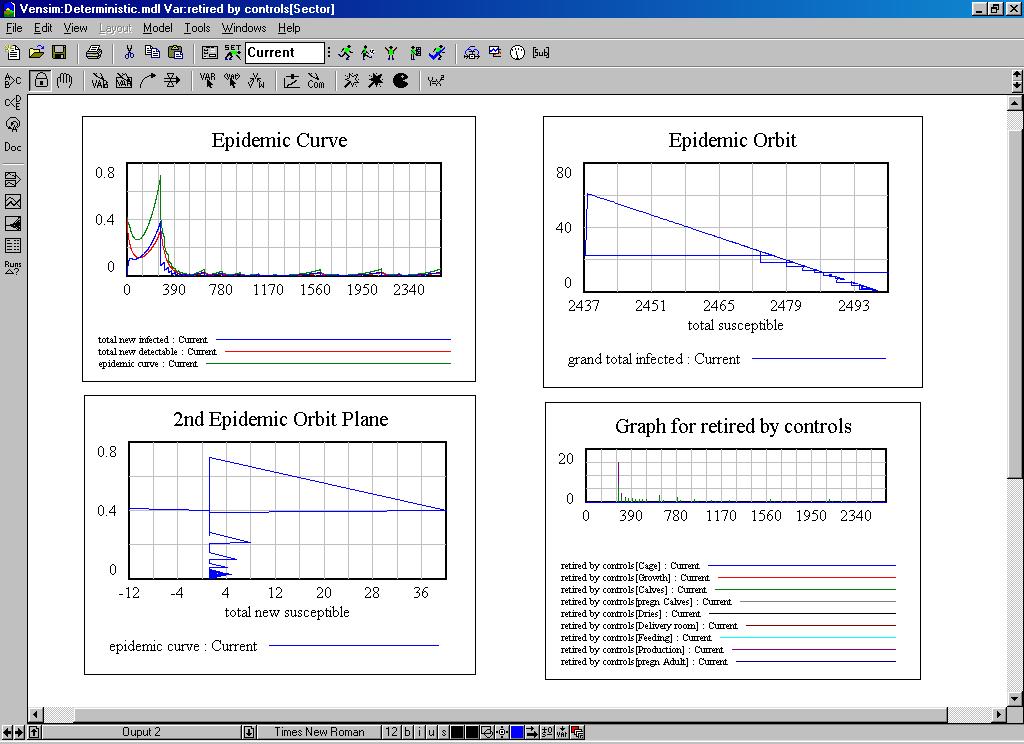
| Figure 6. Some dynamic graphs of the system dynamics model |
|
| Figure 7. The behaviour of the system dynamics model |
| registry data | state of health | position in the farm |
| sex | state | arrival time at the farm |
| birth time | infection time | arrival time in the sector |
| insemination time | infection factor | spatial coordinates |
| pregnancy | disease detection time | actual sector |
| number of deliveries | the state of health of the mother (at parturition time) | colour of the cow, to visualise the state |
| last parturition time | ||
| Farm's Parameters | Test Result | Effects | Next test Interval[5] | ||
| Quarantine | Last Test Interval | Qualification | New Quarantine | ||
| NO | Normal | Negative | YES | NO | Normal |
| NO | Normal | Positive | NO | NO | Very Short |
| NO | Very Short | Negative | NO | YES | Short |
| NO | Very Short | Positive | NO | NO | Very Short |
| YES | Short | Negative | YES | NO | Normal |
| YES | Short | Positive | NO | NO | Very Short |
|
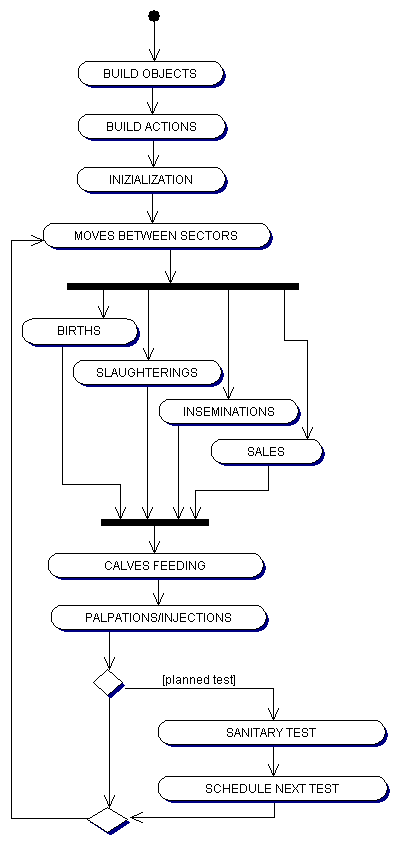
| Figure 8. The structure of the agent based simulation |
|
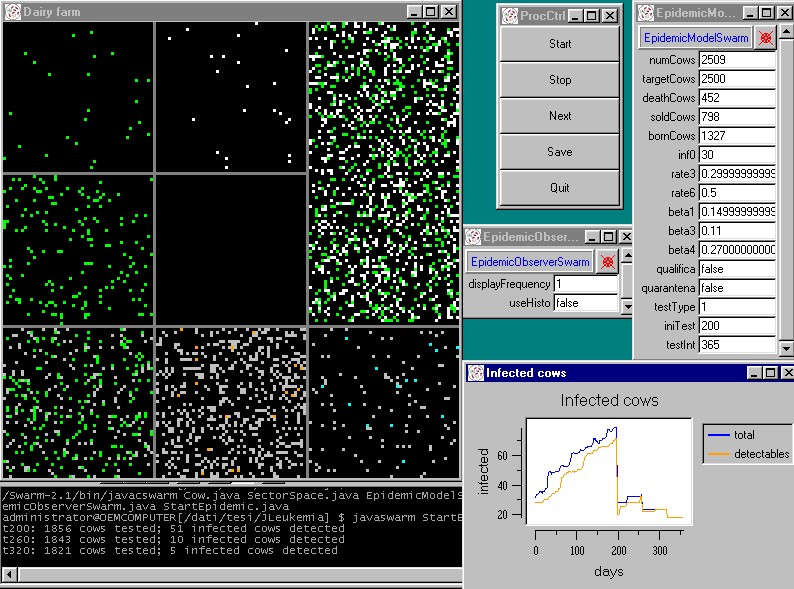
| Figure 9. A simulation experiment in the agent based model |
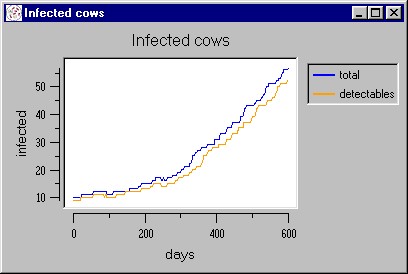
|
| Figure 10. A simulated epidemic waves caused by the palpation/injections factor |
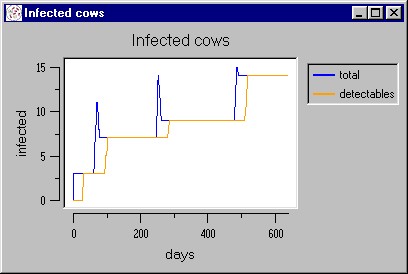
|
| Figure 11. A simulated epidemic waves caused by the vertical forms of transmission |
2 The Unified Modelling Language (UML) is a language for specifying, visualizing, constructing and documenting the artefacts of software systems, as well as for business modelling and other non-software systems. The UML represents a collection of the best engineering practices that have proven successful in the modelling of large and complex systems.
3 that is the resistance to contract the infection following exposure to infective factors.
4 Note that the state "detected infected" is not needed because cows that have a positive result at a sanitary test are immediately separated from the others, even if they are butchered a few days after.
5 Note that, according to the Italian policy for the bovine leukemia control, we have roughly approximated these intervals assuming that when the farm doesn't exhibit cases of infection, the sanitary test are scheduled every year (normal interval), while a test with at least a positive animal determine a following test after two months (very short interval) and the quarantine period is about four months (short interval).
6 In the medical literature, this is called the 'Iceberg Principle'.
BANKS J. (1998) Handbook of Simulation: Principles, Methodology, Advances, Applications, and Practice. John Wiley & Sons.
BARTLETT M. S. (1960) Stochastic population models in ecology and epidemiology. Methuen, London.
BILLARD L. (1973) Factorial moments and probabilities for the general stochastic epidemic. J. Appl. Prob., 10, pp. 277-288.
BOOCH G. (1999) The Unified Modeling Language User Guide. Addison-Wesley.
ELVEBACK L., Ackerman E., Gatewood, L. and Fox, J.P. (1971) Stochastic two-agents epidemic simulation models for to community of families. Am. J. Epidem., 93, pp. 267-280.
ELVEBACK L. (1971) Simulation of stochastic discrete-time epidemic models for two agents. Adv. Appl. Prob., 3, pp. 226-228.
EWY W., Ackerman E., Gatewood L., Elveback, L. and Fox, J.P. (1972) To generalized stochastic model for simulation of epidemics in to heterogeneus population (model You). Comp. Biol. Med., 2, pp. 48-58.
FORRESTER J.W. (1961) Industrial Dynamics, The MIT press.
GALLOP R. J. (1999) Modeling General Epidemics: SIR MODEL, Proceedings of the 12th Annual NorthEast SAS( Users Group Conference.
GANI J. (1969) A chain binomial study of inoculation in epidemics. Bull. I. S. I., 43(2), pp. 203-204.
GANI J. and Jerwood, D. (1971) Markov chain methods in chain binomial epidemic models. Biometrics, 27, pp. 591-604.
GILBERT N. and Troitzsch K. G. (1999) Simulation for the Social Scientist. Open University Press.
HOPPENSTEADT F. (1975) Mathematical Theories of Populations: Demographic, Genetics and Epidemics. SIAM Regional Conference Series in Applied Mathematics 20.
JOHNSON P. and Lancaster, A. (2000) Swarm User Guide http://www.swarm.org
KERMACK, W.O. AND MCKENDRICK, A.G. (1927) Contributions to the mathematical theory of epidemics. Proc. Roy. Soc., To 15, (Part I, 1927).
KENDALL D.G. (1956) Deterministic and stochastic epidemics in closed populations. Proc. Third Berkeley Symp. Math. Statist. & Prob., 4, pp. 149-165.
LAW A.M. and Kelton W.D. (2000) Simulation Modeling and Analysis, Third Edition. McGraw-Hill.
LUNA F. and Stefansson B. (2000) Economic Simulations in Swarm, Agent-based Modelling and Object Oriented Programming, Kluwer.
RENSHAW E. (1991) Modeling Biological Population in Space and Time. New York, NY: Cambridge University Press.
RITCHIE-DUNHAM J.L. (1995a) Application of Systems Thinking in the Mexican Health Sector: An Epidemiological Case Study of Decision Policies in Combating Hemorrhaging Dengue, Third International Decision Sciences Institute Meeting, Puebla, Mexico.
RITCHIE-DUNHAM J.L. (1995b) "Evaluating Policies/Strategies to Combat Epidemics with Systems Thinking", http://www.sdsg.com/new/appbntrf.htm
SARGEANT J. M., KELTON D.F., MARTIN S. W. AND MANN E.D. (1997) Association between farm management practices, productivity, and bovine leukaemia virus infection in Ontario dairy herds. Preventive Veterinary Medicine, 31.
SWARM DEVELOPMENT GROUP (2000) Swarm 2.1 Reference Guide, http://www.swarm.org.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2002]