Would society be better off, in aggregate economic terms, if altruism was more widely practiced among its members? Here I try to answer this question using an agent based computer simulation model of a simple agricultural society. A Monte Carlo exploration of the parameter landscapes allowed the exploration of the range of possible situations of conflict between the individual and the group. The possible benefit of altruism on the aggregate wealth of society was assessed by comparing the overall efficiency of the system in accumulating aggregate utility in simulations with altruistic agents, and with equivalent systems where no altruistic acts were allowed. The results show that no simple situation could be found where altruistic behavior was beneficial to the group. Dissipative and equitative altruistic behavior was detrimental to the aggregate wealth of the group or was neutral. However, the modeling of non-economic factors or the inclusion of a synergic effect in the mutualistic interactions did increase the aggregated utility achieved by the virtual society.

Keywords:

Altruism; Economy; Generosity; Interactions; Mutualism

Introduction

1.1

An altruistic behavior is defined as benefiting others at a cost to the altruist. Yet, altruism can be viewed in a much broader context, and can be classified as a specific case of a reciprocal interaction among two or more individuals. In most such "mutualistic" acts, the distribution of benefits between the actors is very likely to be asymmetrical. That is, one intervening actor benefits more than the other. We might thus conceive mutualism as a more general concept than altruism, where extreme asymmetry in mutualistic transactions is equivalent to altruistic acts. Thus, altruism and reciprocal altruism, represents but a small part of a continuous range of possibilities of mutualistic interactions.

1.2

Extreme cases of altruism, in which an individual sacrifices its reproductive potential or its life in order to favor another individual, are common in nature and have been successfully explained in several cases by kin selection theory (Hamilton 1964) providing the basis for Sociobiology (Wilson 1976). However, kin selection theory does not explain all social phenomena that involve altruistic acts (see Queller et al. 2000, for example). A conspicuous lack of genetic relatedness among certain social wasps, for example, calls for alternative explanations to kin selection (Arathi and Gadagkar 1998). Some alternative explanations have invoked mutualism to explain apparently altruistic acts among social individuals (Axelrod and Hamilton 1981, Clark and Sefton 2001) or have invoked some completely different mechanism to explain the existence of altruism such as docility and learning by example (Simon 1990). Experimental studies have found that the advantages of maintaining a complex web of interpersonal social relationships (Palmer 1991) and social roles (Froming et al. 1985) modulate or mediate altruistic behavior.

1.3

Mathematical models have advanced our understanding of the working of altruism in so far as they show that altruism is an unlikely phenomenon to occur (Nakamaru, Matsuda and Iwasa 1998, Nowak and Sigmund 1998, Zeggelink, DeVos and Donald 2000, Clark and Sefton 2001, for example). Yet, for the study of complex dynamic systems, computational models promise to be more helpful than analytical methods. For example, recent agent based computer simulations of biological evolution suggested that economic considerations, rather than kinship, are better predictors of social behavior, aspects that were ignored in analytical studies. Specifically, the simulations suggest that the evolutionary emergence of altruistic acts requires the existence of social synergy or dynamic effects that augment the benefit beyond the sum of the interacting parts (Jaffe 2001).

1.4

Altruism is intuitively, although not explicitly, thought of as beneficial to the species and/or to the group the altruistic individuals belong. That is, most people feel that in economic terms (total aggregate wealth), a society would be better off if altruism was widespread. For example, the answer to the question posed to 127 scientists attending international meetings^[1] during 2001: Would society be better off, in aggregate economic terms, if altruism was more widely practiced? was Yes in 97.6% of the cases. A proof for this belief, however, is lacking. Here I want to explore the forces that are at work allowing altruism to emerge in cultural evolution, focusing on the aggregate benefits of altruism to the group.

1.5

The term "economic improvement" is used in economics to refer to three different, but closely related things. A Pareto improvement is a change that makes somebody better off and nobody worse off. A potential Pareto improvement, sometimes referred to as a Kaldor improvement, is a change that would be a Pareto improvement if combined with a suitable set of cash transfers among those affected. A net improvement, also called a Marshall improvement--is a change whose net value is positive, meaning that the total value to those who benefit is larger than the total cost to those who lose (Becker 1974, Friedman 1987). The least strict meaning for economic improvement or aggregate increase in wealth is the Marshall improvement, which will be used here.

1.6

Economists have had diverse approaches to the study of aggregate effects of altruistic behavior, but no clear conclusion yet seemed to have emerged. For example, Cheng and Wagener (1992) examined two types of altruism and their implications for voluntary giving. Philanthropists, wishing to enhance the well-being of others, and individuals with merit-good preferences wishing to further the consumption of certain merit goods by others. Philanthropic donors preferred to make cash donations, while donors with merit-good preferences preferred to give in kind. The author suggested that no equilibrium was efficient if there were multiple donors with strategic interaction amongst them.

1.7

An important problem is a lack of consensus on what is meant by altruism. For example, reciprocal altruism, as used by game theorists and economists, is referred to by biologists as mutualism. Here I will introduce a more objective definition of altruism.

Defining altruism

2.1

There are at least three dimensions to the definition of altruism.

1. A unidirectional dimension of altruistic interactions, in which different relationships between the cost of the utility donated by the altruistic agent (K) and the benefit received by the recipient of the altruistic act (A) can be envisioned. If K > A then we might speak of a dissipative transfer of utility, K = A represents an equitative transfer and K < A represents a synergistic transfer, where the value of the utility received by the recipient is higher than the value assigned to the utility by the donor.
2. A second dimension refers to the mutualistic or bi-directional character of the transaction. Here the focus is on the relation between costs to the donor of the utility donated K and the eventual benefit B the donor may recover in the future. Here K could become an investment. A true altruistic act will require that K > B. If K < B then the transaction is actually a commercial one, as K constitutes an investment instead of a donation. An equitative or neutral transaction would imply K = B, which is the case of classical mutualism.

   Tabulating the different possible combinations allows us to define more precisely the different types of mutualistic interactions:

   Uni-directional considerations	Bi-directional considerations	Effect on donor	Effect on recipient	Aggregate effect	Type of interaction
   K > A	K > B	-	+	?	Dissipative altruism
   K < A	K > B	-	+	+ or -	Synergistic altruism
   K = A	K > B	-	+	?	Efficient altruism
   K > A	K < B	+	+	+	Dissipative business
   K < A	K < B	+	+	+	Synergistic business
   K = A	K < B	+	+	+	Efficient business
   K > A	K = B	0	+	?	Dissipative mutualism
   K < A	K = B	0	+	+	Synergistic mutualism
   K = A	K = B	0	+	?	Efficient mutualism
   K = cost to the donor, A = benefit to the recipient, B = benefit to the donor

   Of the different types of interactions listed, the three related to business, even the dissipative one, may be beneficial to society, as is demonstrated by classical economic theory. Synergistic mutualism is an evolutionarily very successful strategy (Jaffe 2001) and is beneficial to the group, and so is synergistic altruism if the amount of utility gained by the recipient is larger than the amount lost by the donor (K - B < A), as the balance of benefits will be necessarily positive. Efficient altruism and the various kinds of mutualism appear to be cases of rather ideal conditions and thus not likely to be found in nature. However, doubt remains about altruisms and mutualisms of the dissipative and efficient kind regarding their impact on aggregate benefits to the group. Here I present results of simulations, exploring the effect on aggregate wealth, of these kinds of interactions.

3. A third dimension can be included into the described scenario. The utility K donated or transferred by the altruist may buy benefits or utilities not measurable in economic terms, such as solidarity, security, belonging, access to paradise, happiness, transcendence, loving care, etc. In such cases, I will refer to utilities in the domain Ψ. That is, we might define the relationship w . e = u + Ψ, where w is work, e its efficiency and u the utility it produces.

Methods

3.1

An agent based computer simulation called sociodynamica, available at http://atta.labb.usb.ve/klaus/klaus.htm, was used to study the effect of the various possible altruistic transactions on wealth accumulation in virtual societies. The model simulates a continuous torus in which agents search for resources (R) in order to survive. Simulating a continuous sphere (the earth's surface for example) eliminates any border effects in the simulations. Each agent acquire a single unit of resource (w_o) each time it encountered a resource, accumulating wealth (w). Agents spend some of their wealth in order to survive, consuming wealth at a basal constant rate (b), which is a fraction of the resource unit. The wealth of each agent changes each time step t :

dw = -b + w_o where w_o = 0 if no resources are encountered.

b determines the degree of external constraints or of competitiveness of the environment and could vary in the range of 1 to 10/w_o

3.2

Agents with no resources left (w = 0) perish. This can be related to the natural metaphor in which organisms die, or to the social metaphor in which companies go bankrupt and dissolve. Agents had movement defined by the distance they displaced themselves in random directions each time step (m) producing a Brownian motion of variable speeds depending on the value of m (range of variation from 0-80 pixels / time step). The movement simulated could represent either physical distance or a two dimensional form of social distance. Each time an agent met another at a distance smaller than a given contact radius (r: range of variation from 0 to 10 pixels), an altruistic act could be triggered depending on the difference in wealth (w₁-w₂) between the two agents and the altruistic threshold (τ) of the agent that moved last. If w₁ / w₂ > τ (the last moving agent was the wealthier by more than the threshold τ: range of variation from 1 to 4 times richer), it transferred wealth to the less wealthy. The amount of wealth transferred depended on the generosity (g) of the last moving agent, and was calculated as (w₁-w₂). g.

3.3

Resources could be either replenished continuously (R_D = 0) or were exhausted after consumption (R_D = 1); they could be concentrated in a single patch (R_N = 1) or in various patches of the same size (R_N = n); and the total amount of resources (R_S) varied from 50 to 500 w_o. Resources were distributed in n sites forming a square in the center of the landscape (R_F = 1) or randomly in the landscape (R_F = 0). The parameter a defined the type of altruistic interaction the agent engaged in. Values for a varied from 1 to 4 indicating respectively dissipative, equitative, synergistic altruism and altruism buying a non-linear, non-economic utility Ψ. When a = 1, 2 or 3, the amount of utility dissipated or gained through altruism was defined by the parameter "altruistic synergy" s = A / K, so that:

s = 0 indicate a 100% dissipation of the utility donated
s < 1 indicate dissipative altruism: Recipient receives less wealth than the altruistic donor spends
s = 1 indicate equitative altruism: Recipient receives the same amount of wealth as the altruistic donor spends
s >1 indicates synergistic altruism: Recipient receives more wealth than the altruistic donor spends

In the simulations presented here, s = 0 when a = 4.

3.4

In real life, there is not always a relationship between increased utility and increased wealth. In a synergistic interaction, if a wealthy donor gives a poor recipient a blanket, the recipient will get a much higher utility from the blanket than the donor, but there is no net increase in wealth. But if the object donated is a sewing machine, which is used in the rich donor's house as decoration, but the poor receiver uses it to produce blankets to sell, then the increased utility might be transformed into increased wealth. It is this second type of synergistic interaction that is modeled here.

3.5

When a = 4, non economic benefits or utility was simulated. This utility, Ψ was simulated as a probability p of achieving a non-economic benefit κ, so that w . e = u + p . κ, where Ψ = p . κ, and κ was survival of the agent. In the simulations presented here, increased generosity increased the survival probability of agents in simulations where 0.2% of agents were killed randomly after each time step.

3.6

A Monte Carlo exploration of the parameter landscape was performed, by randomly assigning values to a, R_D, R_N, R_S, R_F, τ, g, m, s and b; and running the simulation for 80 time steps (unless stated otherwise) for 2000 agents engaging in dissipative or equitative altruism.

3.7

For each simulation, the total wealth accumulated by a population (GDP, for gross domestic product) of either egoist (g = 0) or altruist (g > 0) agents was calculated as GDP = Σw_i. The difference Δ = GDP(egoist) - GDP(altruist) was computed. Values of Δ < 0 indicated that the given combination of parameters produced simulations where the altruistic behavior of agents improved the cumulative wealth of the society of agents. As the simulations contained highly stochastic aspects, such as the movement of the agents and the location of the resources, numerous simulation were run and results were analyzed using regression analysis.

Results

4.1

The agent-based model was complex enough for unexpected properties to emerge from the simulations. Figure 1 shows the effect of environmental constraints or degree of competitiveness b on the aggregate utility (or cumulative wealth) we called GDP, of the population of simulated agents. Under a given pattern of resource distribution, agents showed divergent behavior regarding their ability to optimize GDP depending on their speed of movement m. They could be classified as either conservative (slow moving: blue and violet dots) or dynamic (fast moving: green dots), where conservative agents maximized GDP at high values of b, whereas dynamic agents did so at low values of b. This difference was due to the fact that different speeds of movement produced a different tracking of the available resources that had a different susceptibility to the parameter b. Altruistic behavior, given by the variable g (indicating the % of utility donated by agents or generosity of agents), did not seem to affect the results of these simulations (compare simulations with g = 0 to those with g = 50).

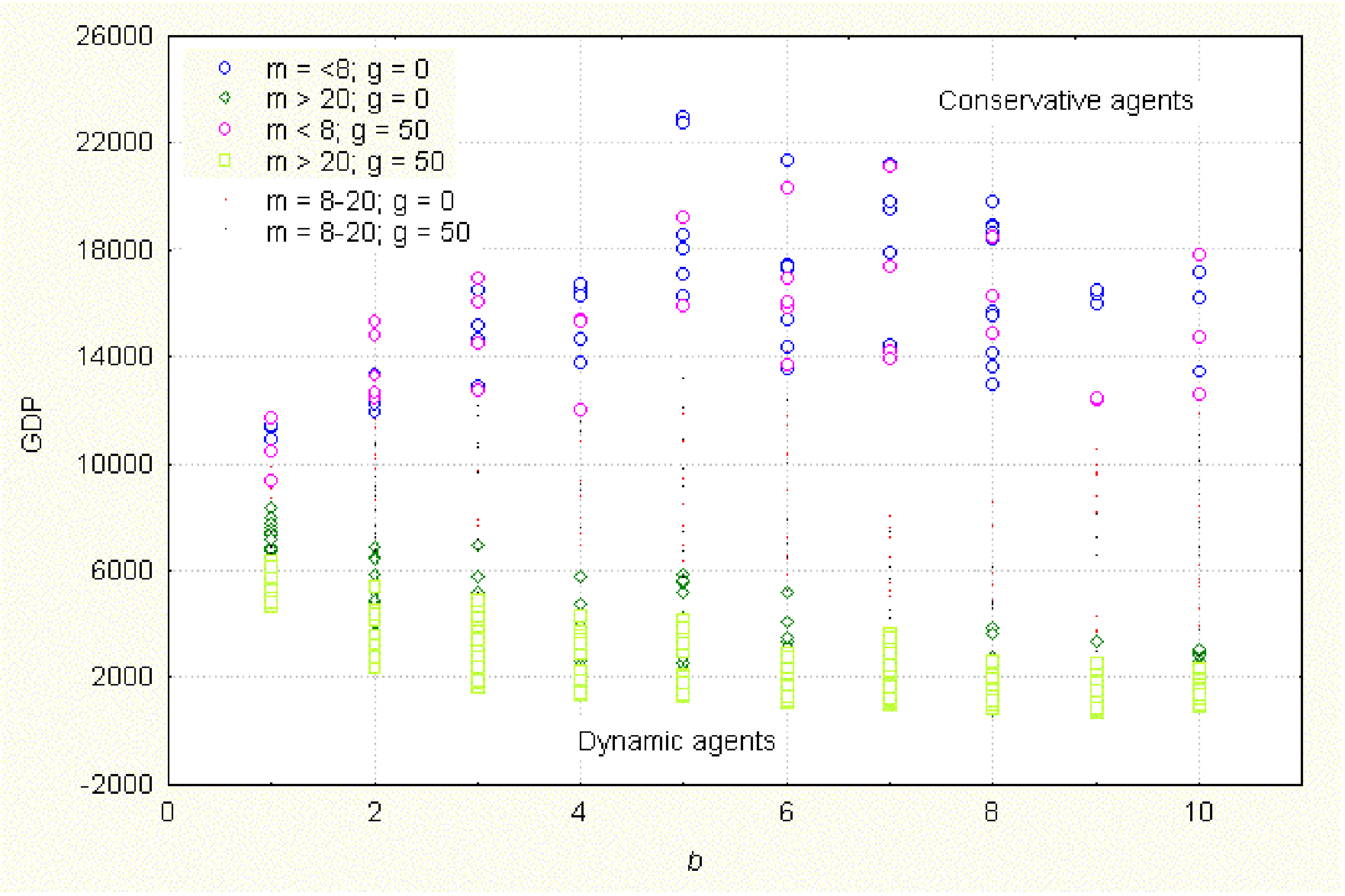
Figure 1. Effect of b, m and g on total accumulated wealth (GDP). tstep = 40, RD = 1, RN = 1, RS = 100, τ = 2, a = 2

4.2

The nature of resources affected the total accumulated wealth of the virtual society of agents (Figure 2). When resources were continuously replenished (R_D = 0) the aggregate wealth accumulated by the agents was much larger than when the resources were exhausted by consumption (R_D = 1). This is a trivial result but serves as a test of the model. However, continuously replenishing resources produced a non-uniform, U shaped dependency between the degree of generosity (g) and the aggregate wealth (GDP).

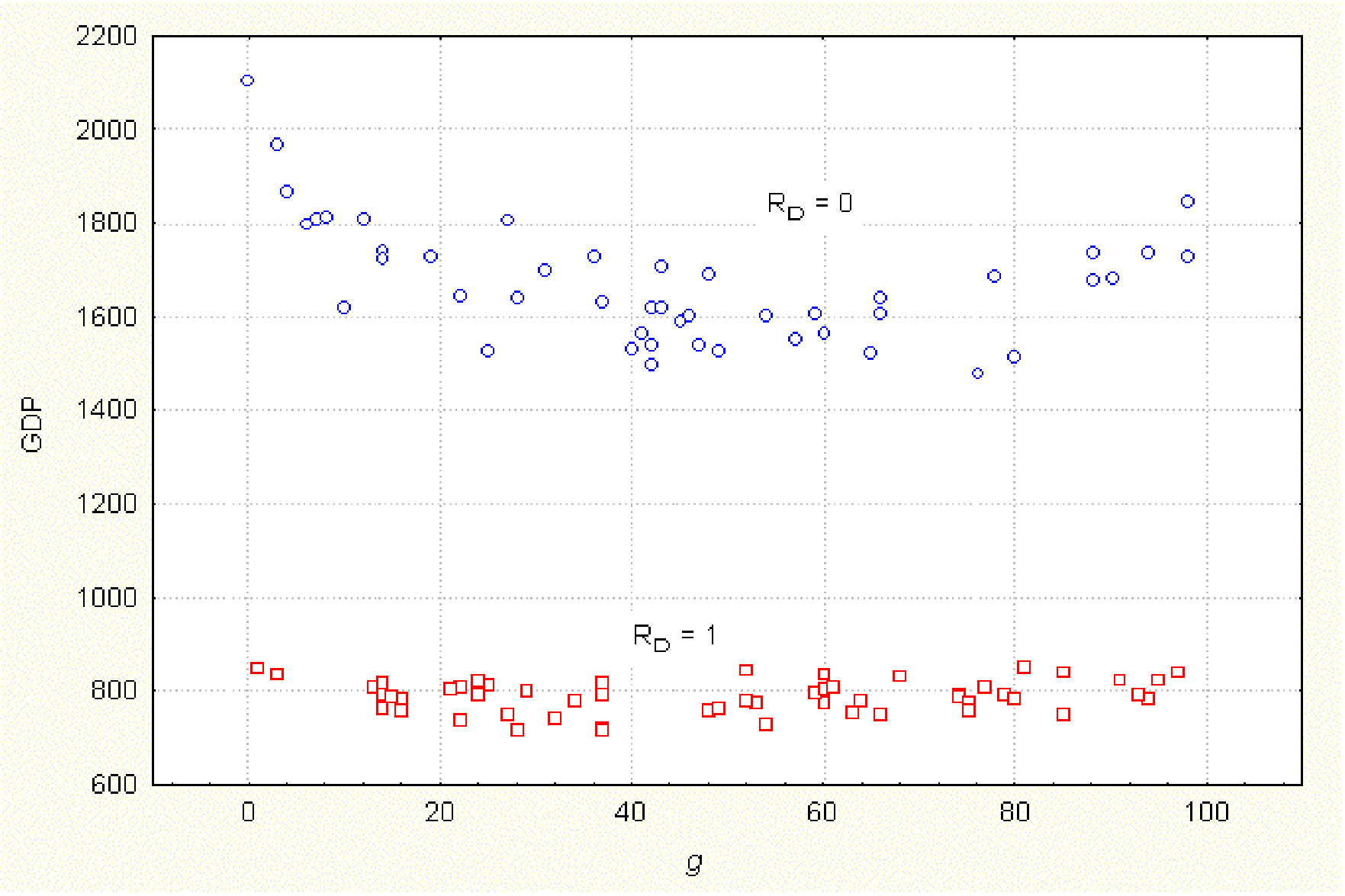
Figure 2. Total wealth accumulated (GDP) vs. generosity (g). tstep = 80, RN = 1, RS = 100, τ = 2, b = 5, m = 20, a = 2

4.3

When simulations of the Monte Carlo variation of the values of the different parameters were run for equitative agents (a = 2), we were unable to find even a single situation where altruistic behavior (positive values of g) produced a higher GDP (i.e. Δ < 0) than egoistic agents (g = 0). Some results from these simulations are presented in Figures 3 to 4. Dissipative altruism (Figure 5) increased Δ even more.

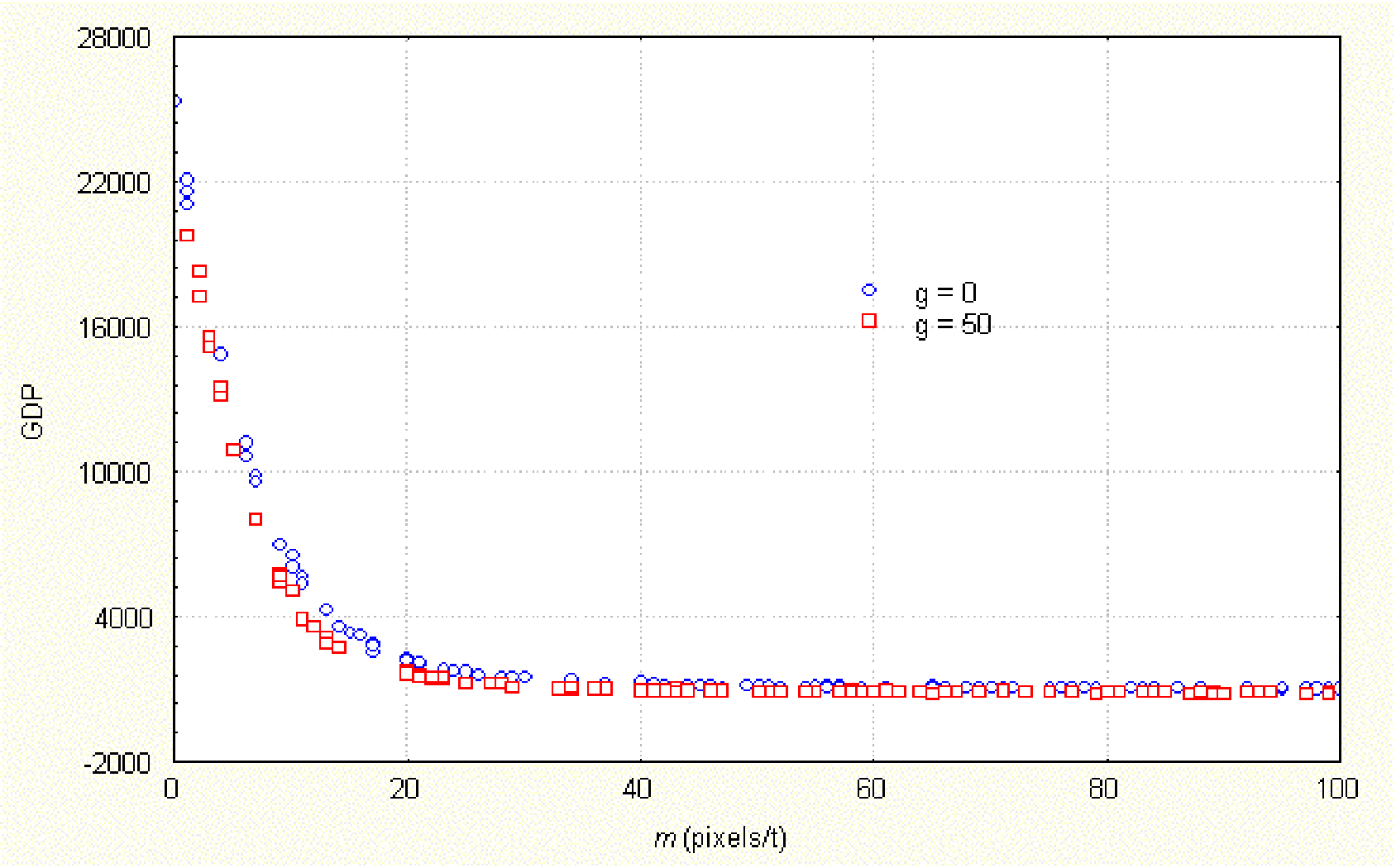
Figure 3. Total wealth accumulated (GDP) at different speeds of movement (m) of agents. tstep = 80, RD = 1, RN = 1, RS = 100, τ = 2, b = 5, a = 2

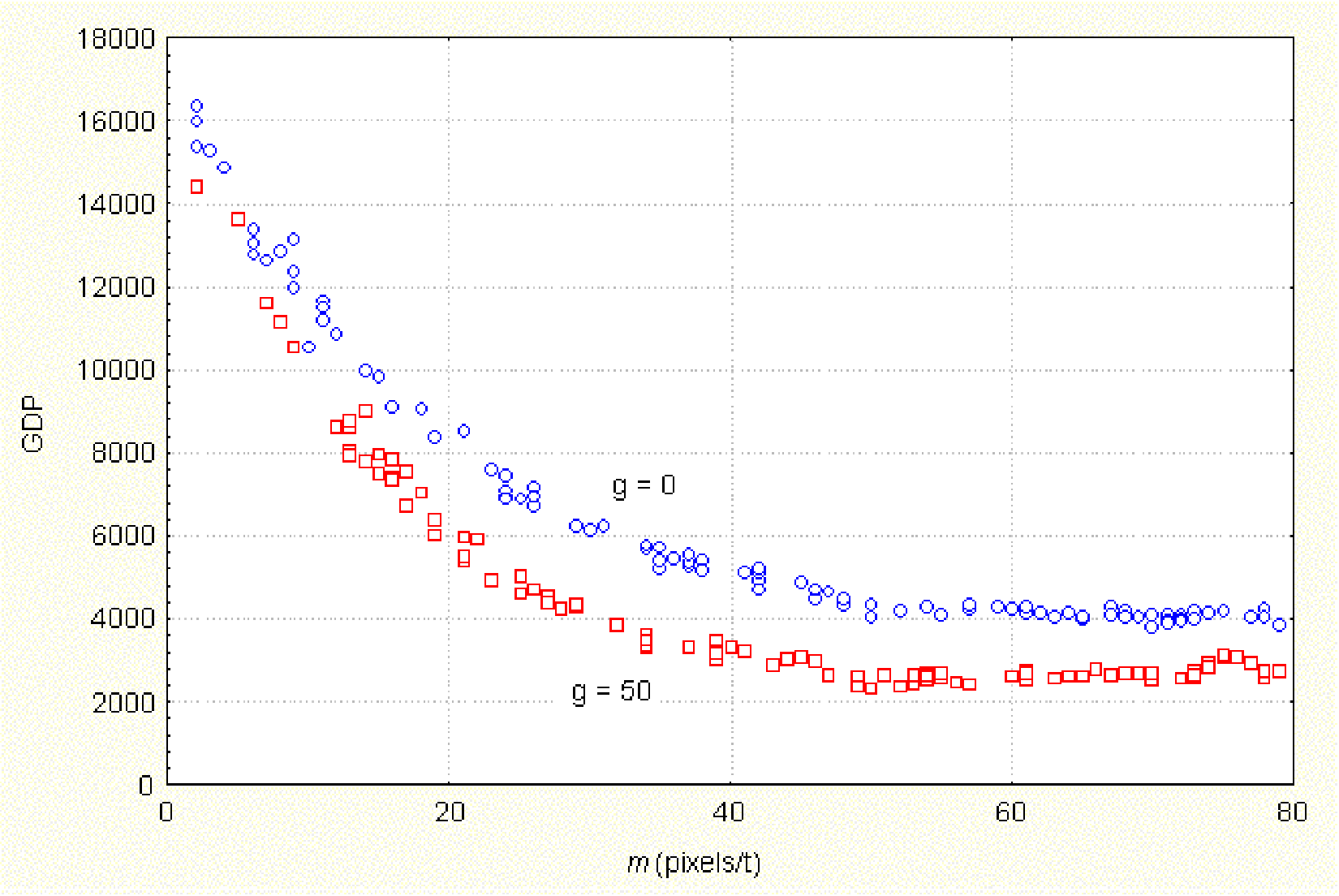
Figure 4. Effect of the speeds of agents (m) on accumulated wealth (GDP). tstep = 40, RD = 0, RN = 1, RS = 100, b = 2, τ = 2, a = 2

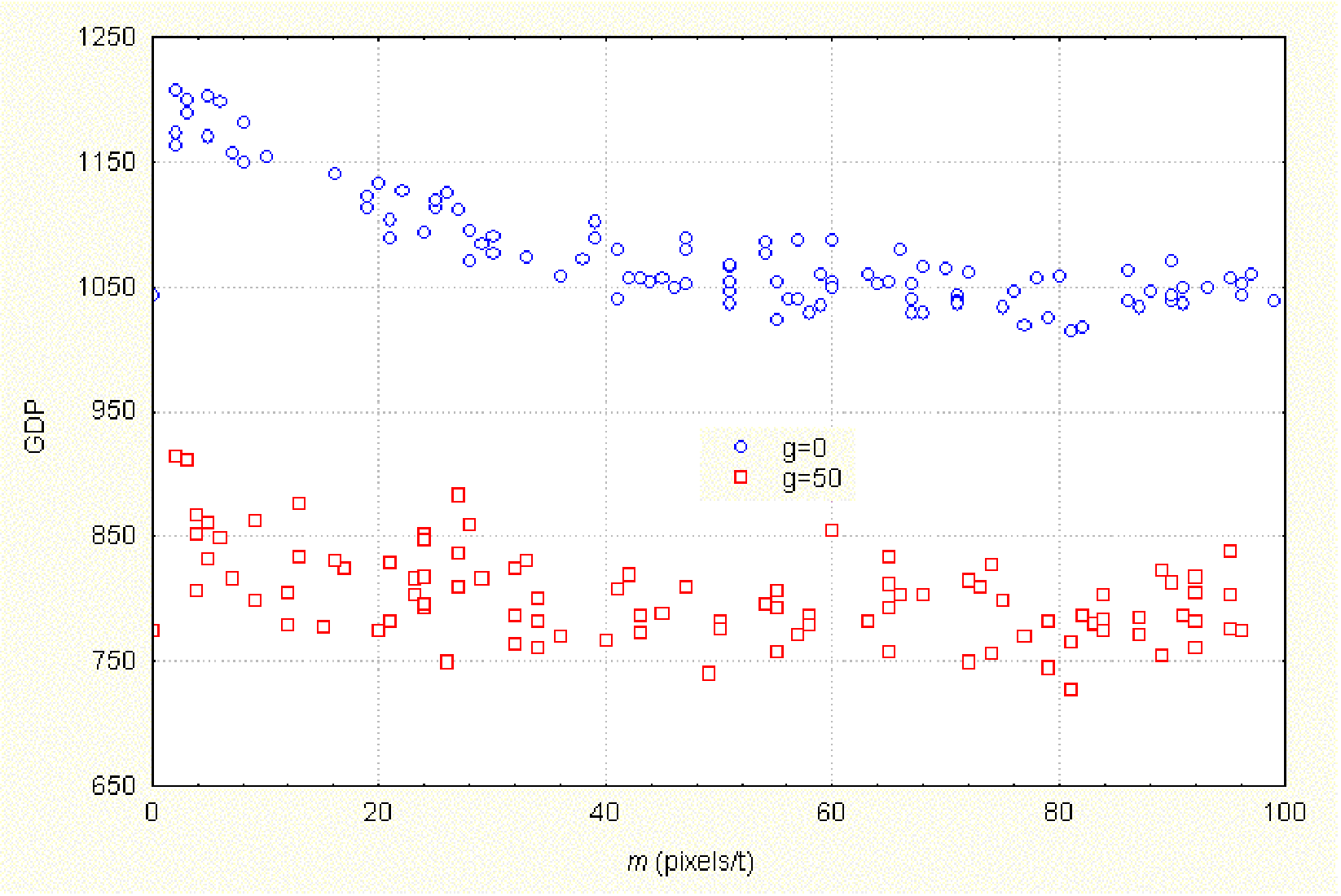
Figure 5. Accumulated wealth (GDP) vs. speeds of movement (m). tstep = 80, RD = 1, RN = 1, RS = 1, τ = 2, b = 5, a = 1

4.4

I used a Monte Carlo approach to study the effect of the parameters on GDP. The values of the parameters were randomly chosen and the simulations were run in order to calculate the GDP. The results are summarized in a regression matrix (Table I)

Table 1: Regression Summary for GDP as Dependent Variable
MULTIPLE R= .59331672 R2= .35202473 Adjusted R2= .34810947, REGRESSION: F(6,993)=89.911 p<0.0000 Std.Error of estimate: 648.25 . Rs * Rn = 100
N=1000	BETA	St. Err. of BETA	B	St. Err. of B	t(1000)	p-level
Intercept			2488.398	99.57890	24.9892	.000000
RN : 1-3	-.240355	.025592	-240.917	25.65139	-9.3920	.000000
RD : 0-1	-.230911	.025619	-370.639	41.12142	-9.0133	.000000
b : 1-10	-.360600	.025584	-101.086	7.17185	-14.0948	.000000
m : 0-80	-.327687	.025587	-11.324	.88423	-12.8066	.000000
g : 0-100	.039650	.025594	1.103	.71223	1.5492	.121650
τ: 1-4	.045711	.025608	32.905	18.43378	1.7850	.074562

MULTIPLE R= .68707494 R2= .47207197 Adjusted R2= .46839046 REGRESSION: F(5,717)=128.23 p<0.0000 Std.Error of estimate: 940.28. Rs = 100, Rn = 1
N=723	BETA	St. Err. of BETA	B	St. Err. of B	t(723)	p-level
Intercept			3690.323	146.0162	25.2734	.000000
RD : 0-1	-.336655	.027238	-868.009	70.2286	-12.3598	.000000
b : 1-10	-.343743	.027184	-154.763	12.2391	-12.6450	.000000
m : 0-80	-.485642	.027274	-26.208	1.4718	-17.8063	.000000
g : 0-100	-.017311	.027228	-.785	1.2345	-.6358	.525139
τ: 1-4	-.007347	.027231	-8.443	31.2943	-.2698	.787396

MULTIPLE R= .68711002 R2= .47212018 Adjusted R2= .46999805 REGRESSION: F(4,995)=222.47 p<0.0000 Std.Error of estimate: 877.46. Rs = 100, Rn = 1, τ= 2
N=1000	BETA	St. Err. of BETA	B	St. Err. of B	t(1000)	p-level
Intercept			3480.976	94.02562	37.0216	.000000
RD : 0-1	-.347609	.023050	-837.840	55.55771	-15.0805	.000000
b : 1-10	-.344063	.023054	-144.109	9.65599	-14.9243	.000000
m : 0-80	-.479049	.023048	-24.835	1.19485	-20.7853	.000000
g : 0-100	-.010569	.023067	-.439	.95865	-.4582	.646913

4.5

The results show that the degree of altruism expressed as g has either no significant correlation with GDP or correlates negatively with GDP.

4.6

However, if synergistic altruistic interactions were simulated (a = 3) or the domain Ψ (non economic benefits for altruistic acts) was included, then altruism produced general benefits to the society of agents (Δ < 0). In Table II, a regression summary of the latter case is presented. Here, agents possessed in addition to the described economic fitness or survival function, the function Ψ. This function increased the likelihood that neighboring agents rescued a given agent from life-threatening circumstances, in proportion to the amount of resources distributed altruistically by the agent (i.e. here generous donations to other agents bought their willingness to help in resolving life threatening problems in the future). The presence of function Ψ in the simulations produced higher GDP for higher altruism. This can be deduced from the positive significant correlation between GDP and the variable g in Table II, when Ψ ≠ 0 is compared to simulations where Ψ = 0, as indicated in the same table.

Table 2: Regression Summary for GDP as Dependent Variable, when non-economic considerations were included in the model
MULTIPLE R= .82476112 R2= .68023090 Adjusted R2= .66322190 REGRESSION: F(5,94)=39.992 p<.00000 Std.Error of estimate: 1988.3 / Rs = 100, Rn = 1, Ψ ≠ 0
N=100	BETA	St. Err. of BETA	B	St. Err. of B	t(94)	p-level
Intercept			13032.57	831.8147	15.66764	.000000
RD : 0-1	-.555703	.058535	-3807.87	401.1005	-9.49356	.000000
b : 1-8	-.266175	.058561	-394.37	86.7660	-4.54524	.000016
m : 0-50	-.281783	.060037	-66.56	14.1824	-4.69348	.000009
g : 0-50	.231442	.059328	54.09	13.8660	3.90107	.000180
τ: 1-4	-.508383	.059106	-1584.98	184.2741	-8.60123	.000000

MULTIPLE R= .82476112 R2= .68023090 Adjusted R2= .66322190 REGRESSION: F(5,94)=39.992 p<.00000 Std.Error of estimate: 1988.3 / Rs = 100, Rn = 1 Ψ = 0
N=202	BETA	St. Err. of BETA	B	St. Err. of B	t(196)	p-level
Intercept			38912.4	1197.985	32.4815	.000000
RD : 0-1	-.709221	.027455	-15711.9	608.224	-25.8324	.000000
b : 1-8	-.325338	.027626	-1472.5	125.032	-11.7766	.000000
m : 0-50	-.462689	.027483	-361.8	21.490	-16.8353	.000000
g : 0-50	-.081932	.027590	-60.9	20.495	-2.9696	.003354
τ: 1-4	.031644	.027498	325.7	283.022	1.1508	.251234

Discussion

5.1

The concept of altruism has been used in a very loosely defined form by many authors, often referring to business interactions with a time delay between the investment and the collection of benefits, which in economic terms is rather normal. Such is the case of reciprocal altruism. Another recent example is tag-dependent independent reciprocal altruism (Riolo et al. 2001). In these cases the "altruist" eventually recovers the cost of the investment it made, eventually making a profit. Thus, the more quantitative definition of altruism given here, which depends on the balance of the variables K, A and B, might lead to a clearer use of the term, and thus to a better understanding of the interactions among individuals of a society. The definitions of altruism used here were forced by the need to design a mathematically comprehensive and coherent model, showing the heuristic value of social simulation models.

5.2

Under this new theoretical framework, most interactions, formerly considered as "altruistic", might indeed be considered selfish in the long term, such as reciprocal altruism, which is just a risky long term investment of the kind that insurance companies are experts in. The simulations suggest that truly altruistic behavior and/or display of generosity towards others is not likely to provide economic benefits to a society. However, in a situation where synergistic effects increase the economic utility received by the beneficiary of the altruistic interaction, we can expect a higher aggregate utility to groups with higher true altruism. This adds to our knowledge that altruistic behavior without synergistic benefits is evolutionary unstable (Jaffe 2001). The simulations showed that dissipative and efficient altruistic behaviors per se are not advantageous to the group or to the individual. As with the laws of thermodynamics, however, this conclusion is based on an absence of evidence to the contrary. Of course, I did not explore all the possible parameter geometries (they are infinite) with the simulations. But altruism clearly benefits society when synergistic effects are present (Jaffe 2001).

5.3

Although in a very different context, a somewhat equivalent result was obtained by Zeggelink et al. (2000), using a Social Evolution Model. They could not find any specific effect on altruism of group size, when studying the conditions under which cooperation is a viable strategy and the conditions under which individuals structure themselves into stable groups.

5.4

I suggest that future experimental research studying altruism will uncover synergisms explaining the apparently altruistic interactions in nature. A heuristic extreme case of synergy is the case of mutualistic brood care. Here, "synergy" increases the fitness of the offspring due to caring adults. More time dedicated to caring for the brood will reduce the odds of parasites or predators killing the offspring. If one parent invests 50% of its time to care for its brood, it will leave the brood unattended 50% of the time, and the odds of losing the brood will be high. If two parents attend their brood communally and synchronically, each one investing 50% of their time in brood care, the brood may be protected 100% of the time, reducing the odds of losing their brood to zero with the same cost to parents. Exploring this kind of synergistic factor helps us to understand the evolution of social behavior. For example, Silva and Jaffe (2002) showed that economic synergies may underlie the evolution of social behavior in wasps, as a strong correlation between social behavior and efficiency in foraging behavior can be found. Another example is given in Cabrera and Jaffe (1998) who showed that efficiency of energy consumption increases in larger human aggregates.

5.5

The simulations showed that when non-economic considerations are included in the model, altruism may become beneficial to society. I simulated Ψ as a probability p of achieving a non-economic benefit κ, so that w . e = u + p . κ , where Ψ = p . κ. In the simulations presented here, κ was survival. Yet, Blaise Pascal in the XVII century showed that if the benefit κ approached infinity (such as the benefit of getting to heaven, in the case of Pascal, or the benefit of staying alive, in the present model) then the probability of obtaining the benefit p could be arbitrarily small and still Ψ will be greater than nil. Clearly, these non-linear effects have a strong influence on the economic behavior of humans that classical economic theory does not account for. Thus, the results of the present simulations suggest that we should expect to find behaviors that are non-rational in economic terms playing a fundamental role in maintaining the cohesiveness of our societies.

5.6

The central theoretical achievement of classical and neoclassical economics is the demonstration, summed up by Adam Smith's metaphor of the 'invisible hand', that the interaction of selfish economic agents may produce a mutually beneficial and Pareto-optimal outcome. Yet, the apparently counterintuitive results presented here suggest that the proposition that altruism should be beneficial in the long term to society is not based on rational economic thinking. Certainly, not all desires and behaviors of humans have a rational basis. For example, Raut (1992) proposed an ethical principle to supplement equilibrium theory for guiding agents in their choice of the degree of altruism towards their parents. Quiggin (1997) suggested that altruism is an expression of moral beliefs rather than of a taste for other people's consumption, and that although the project of treating moral beliefs as preferences has some appeal for economists, it is unlikely to be successful. The simulation results presented here build on these conclusions, suggesting that in pure economic terms, altruism can lower society's level of aggregate wealth, except in the case of synergistic altruism, and that non-economic factors might well explain the existence of altruistic behavior.

Acknowledgements

I thank the two anonymous referees for their excellent reviews.

Notes

¹ The meetings were:

Society for Advancement of Behavioral Economics (SABE), Biennial Conference, George Washington University, Washington DC, USA, June 11-12, 2001
Computational and Mathematical Organization Theory Conference, July 5 - 8 2001, Carnegie Mellon University, PA, USA
International Conference on Mathematical and Theoretical Biology, and Annual Meeting of the Society for Mathematical Biology, Joint with Japan Association of Mathematical Biology, Hilo, Big Island, Hawaii, July 16-19, 2001

Glossary

A	Utility received by altruistic beneficiary (benefit to the recipient)
K	Utility donated by altruistic agent (cost to the donor)
B	Long term benefits received by donor of utility (benefit to the donor)
b	Degree of external constraints and/or degree of competitiveness
m	Maximum distance of random movement of agents
g	Degree of generosity Percentage of excess resources donated by agent
τ	Threshold in wealth difference that triggers altruistic donation
RD	Renewable resources (0) or non renewable (1) resources
RN	Number of patches the resource was distributed in space
RS	Size of the resource in wo
RF	Pattern of the distribution of resource patches 0 random, 1 centered
a	Type of altruism simulated
wo	Unit for resource
wi	Resources accumulated by agent i
GDP = Σwi.	Resources accumulated by the whole population
Ψ	Domain of non economic utilities
w	Work
e	Efficiency
u	Utility
p	Probability
κ	Amount of non economic utility

References

ARATHI, H.S. and GADAGKAR, R. 1998. Cooperative nest building and brood care by nestmates and non nestmates in Ropalidia marginata: implications for the evolution of eusociality. Oecologia 117: 295-299.

AXELROD, R. and HAMILTON, W.D. 1981. The evolution of cooperation. Science 211:1390-1396

BECKER, G.S. 1974. A Theory of Social Interactions, J. Political Economics, 82:1063-1091

CABRERA, S. and JAFFE, K. 1998. On the energetic cost of human societies: energy consumption as an econometric index. Interciencia 23: 350-354.

CHENG, S.W. and WAGENER, A. 1992. Altruism and Donations http://www.uni-siegen.de/dept/fb05/vwliv/doks/92-00.pdf

CLARK, K. and SEFTON, M. 2001. The sequential prisoner's dilemma: Evidence on reciprocation. Economic Journal 111: 51-68

FRIEDMAN, D.D. 1987. Does Altruism Produce Efficient Outcomes? Marshall vs. Kaldor." Journal of Legal Studies, Vol. XVII. http://www.daviddfriedman.com/Academic/Marshal_Pareto/Marshal_Pareto.html

FROMING, W.J., ALLEN, L. and JENSEN, R. 1985. Altruism, role-taking and self awareness: The acquisition of norms governing altruistic behavior. Child Development 56: 1223-1228

HAMILTON, W.D. 1964. The genetic evolution of social behaviour I and II. Journal of Theoretical Biology 7: 1-16 and 17-52.

JAFFE, K. 2001. On the relative importance of Haplo-Diploidy, Assortative Mating and Social Synergy on the Evolutionary Emergence of Social Behavior. Acta Biotheoretica 49: 29-42.

NAKAMARU,M., MATSUDA, H. and IWASA. Y. 1998. The Evolution of social interaction in lattice models. Sociological Theory and Methods 12: 149-162.

NOWAK, M.A. and SIGMUND, K. 1998. Evolution of indirect reciprocity by image scoring. Nature, 393: 573

PALMER, C.T.1991. Kin-selection, reciprocal altruism and information sharing among Maine lobstermen. Ethology and Sociobiology 12: 221-235.

RAUT L.K. 1992. Two-sided altruism, Lindahl Equilibrium, and Pareto Optimality in Overlapping Generations Models http://137.151.62.161/Research/Papers/Working/lindahl.pdf

RIOLO, R.L., COHEN, M.D. and AXELROD, R. 2001. Evolution of cooperation without reciprocity. Nature414, 441 - 443.

SIMON, H.A. 1990. A mechanism for social selection and successful altruism. Science, 250: 1665-1668

SILVA, E.R. and JAFFE, K. 2002. Expanded food choice as a possible factor in the evolution of eusociality in Vespidae Sociobiology 39:25-36.

WILSON, E.O. 1976. Sociobiology: A New Synthesis, Harvard University Press.

QUELLER, D.C., ZACCHI, F., CERVO, R., TURRILLAZZI, S., HENSHAW, M.T., SANTORELLI, L.A. and STRASSMANN J.E. 2000. Unrelated helpers in a social insect. Nature 405: 784-787.

QUIGGIN, J. 1997. Altruism, total valuation and benefit cost analysis. Australian Economic Papers 36 (68), 144-155. http://ecocomm.anu.edu.au/quiggin/JournalArticles97/Altruism97.pdf

ZEGGELINK,E.P.H., DEVOS, H. and DONALD, E. 2000. J. Artificial Societies and Social Simulation,https://www.jasss.org/3/3/1.html.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2002]