Kurt A Richardson (2002)
"Methodological Implications of Complex Systems Approaches to Sociality": Some Further Remarks
Journal of Artificial Societies and Social Simulation
vol. 5, no. 2
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/5/2/6.html>
Received: 18-Feb-2002 Published: 31/3/2002
 Abstract
AbstractPremise 1: There are simple sets of mathematical rules that when followed by a computer give rise to extremely complicated patterns.
Premise 2: The world also contains many extremely complicated patterns.
Conclusion: Simple rules underlie many extremely complicated phenomena in the world, and with the help of powerful computers, scientists can root those rules out.

|
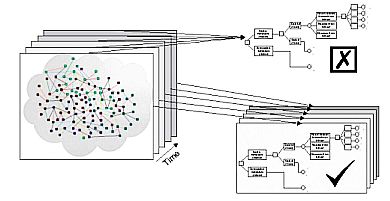
| Figure 1. Illustration showing that not only can a particular system state (outcome) can be reached via different trajectories from the same starting conditions, but also that different starting conditions may also lead to the same system state. Of course, the reverse case is also a possibility in that different starting conditions may lead to different outcomes and multiple runs from the same starting conditions may also result in different outcomes. |
|
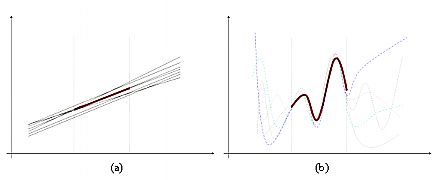
| Figure 2. Linear models of a linear universe versus nonlinear models of a nonlinear universe. (For linear systems extrapolation from limited data is a trivial exercise, whereas for nonlinear systems extrapolation from limited data is a highly problematic exercise. |
|
| Figure 3. The 'evolution' of a linear 'decision tree' model |
2Which are often no more than statistical correlations rather than causal explanations.
3Even the act of modeling itself may affect the real system in nontrivial ways.
4Bankes & Gillogly (1994) and Bankes (1993) recognize the impossibility of validating exploratory models and suggest that we must instead validate our research strategies (i.e. the validation of the modeling process).
BANKES, S. & GILLOGLY, J. (1994). "Validation of Exploratory Modelling," Proceedings of the Conference on High Performance Computing, Adrian M. Tentner and Rick L. Stevens (eds.), San Diego, CA: The Society for Computer Simulation, pp. 382-387.
BANKES, S. (1993). "Exploratory Modelling for Policy Analysis," Operations Research, Vol. 41 No. 3: 435-449.
FLOOD, R. L. (1989). "Six Scenarios for the Future of Systems 'Problem Solving'," Systems Practice, 2(1): 75-99.
FLOOD, R. L. and ROMM, N. R. A. (eds.) (1996). Critical Systems Thinking: Current Research and Practice, Plenum Press: NY, ISBN 0306454513.
FLOOD, R. L. (2001). "Local Systemic Intervention," European Journal of Operational Research, 128: 245-257.
GOLDSPINK, G. (2002). "Methodological Implications of Complex Systems Approaches to Sociality: Simulation as a Foundation for Knowledge," Journal of Artificial Societies and Social Simulation, Vol. 5, No. 1, <https://www.jasss.org/5/1/3.html>.
HORGAN, J. (1995). "From Complexity to Perplexity," Science, 272: 74-79.
JACKSON, M. C. (2001). "Critical Systems Thinking and Practice," European Journal of Operational Research, 128: 233-244.
KOLLMAN, K., MILLER, J. H. and PAGE, S. (1997). "Computational Political Economy," in Arthur, W. B., Durlauf, S. N. and Lane, D. A. (eds.), The Economy as an Evolving Complex System II, Addison-Wesley: Reading MA, ISBN 0201328232.
MIDGLEY, G. (2000). Systemic Intervention: Philosophy, Methodology, and Practice, Kluwer Academic / Plenum Publishers: NY, ISBN 0306464888.
ORESKES, N., SHRADER-FRECHETTE, K. and BELITZ, K. (1994). "Verification, validation, and Confirmation of Numerical Models in the Earth Sciences," Science, 263: 641-646.
RICHARDSON, K. A. (2001). "On the Status of Natural Boundaries: A Complex Systems Perspective ," Proceedings of the Systems in Management - 7th Annual ANZSYS conference November 27-28, 2001: 229-238, ISBN 072980500X.
RICHARDSON, K. A. (2002). "The Hegemony of the Physical Sciences - An Exploration in Complexity Thinking," submitted for inclusion in a forthcoming edited book Living with Limits to Knowledge. Available here.
RICHARDSON, K. A. and CILLIERS, P. (2001). "What is Complexity Science? A View from Different Directions," Special Issue of Emergence - Editorial, Vol. 3 Issue 1: 5-22.<http://www.kurtrichardson.com/Editorial_3_1.pdf>
RICHARDSON, K. A., MATHIESON, G. and CILLIERS, P. (2000). "The Theory and Practice of Complexity Science - Epistemological Considerations for Military Operational Analysis," SysteMexico, 1: 25-66. <http://www.kurtrichardson.com/milcomplexity.pdf>
VON BERTALANFFY, L. (1969). General System Theory: Foundations, Development, Applications, George Braziller: NY, Revised Edition, ISBN 0807604534.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2002]