Dietrich Stauffer (2001)
Monte Carlo simulations of Sznajd models
Journal of Artificial Societies and Social Simulation
vol. 5, no. 1
<https://www.jasss.org/5/1/4.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 4-Dec-01 Accepted: 22-Jan-02 Published: 31-Jan-01
 Abstract
AbstractWe do not deal here with all the variants but emphasize the more interesting ones. The next section looks at the basic model, then we check complications and compare the results with the Ising model at low temperatures, and finally we describe a political application, the distribution of votes among candidates. The crucial difference between the Sznajd model and voter or Ising models is that information flows outward: a site does not follow what the neighbours tell the site, but instead the site tries to convince the neighbours.

|

|
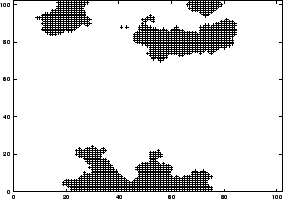
|
| Figure 1.Sznajd square lattice, with a parallel pair convincing its six neighbours, after 1, 5 and 50 iterations. After 256 iterations the whole lattice was empty (spin down). |
For these rules in one and two dimensions (and also for the majority of alternative rules (Stauffer, Sousa and Moss de Oliveira 2000)) the system always ends up at a fixed point: either all spins point up, or they all point down in the square lattice. The antiferromagnetic rule in one dimension (Sznajd-Weron and Sznajd 2000) in addition allows in half of the cases an antiferromagnetic ordering of up, down, up, down etc. (In ferromagnets, neighbouring magnetic dipoles want to align parallel, while in antiferromagnets, neighbours want to be opposite to each other.) The times needed to reach this fixed point increase with lattice size and are distributed log-normally or in a more complicated way, depending on the rule (Stauffer, Sousa and Moss de Oliveira 2000). Thus the problem is quite time consuming and does not allow one to simulate even medium-size lattices like 1000 × 1000.
Usually one starts with half of the spins up and half of the spins down. If one varies the initial concentration p of up spins, one sees a phase transition in the above rule for the square lattice but not for the chain. The system finally has all spins down if p < 1/2 and all spins up if p > 1/2. In a finite lattice, of course, phase transitions are never sharp, and thus the transition is indicated numerically by a slope (Figure 2) becoming steeper and steeper the larger the lattice is. In an infinite lattice, one would get a sharp step function for the number of up fixed points versus the initial concentration p. This holds for both a regular square lattice (Stauffer, Souse and Moss de Oliveira 2000) as well as for one where a fraction of sites is removed in a correlated way (Moreira, Andrade and Stauffer 2001).
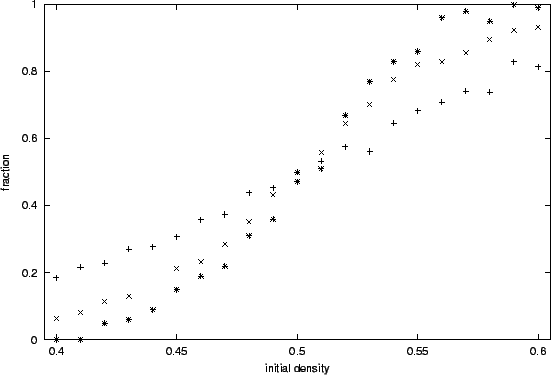
|
| Figure 2. Fraction of samples ending with all spins up, versus initial fraction of up spins. 1000 samples L = 23 (+, 1000 samples), 53 (x, 1000 samples) and 101 (*, 100 samples), on a correlated-diluted square lattice (Moreira, Andrade and Stauffer 2001). |
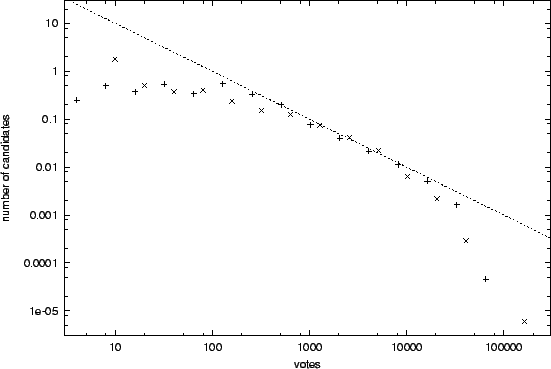
|
| Figure 3. Comparison of simulated votes (+) with real votes (x). From Bernardes (Bernardes, Costa et al 2001). |
I thank Suzana Moss de Oliveira and Paulo Murilo C. de Oliveira for hospitality at UFF in Niterói, Brazil, where most of this work was done together with Brazilian collaborators.
program sznajd
c square lattice, with two neighbours convincing
parameter(L=101, L2=L*L, Ls=L2+4*L)
dimension nhist(0:32), neighb(0:3), is(Ls)
data maxstep/90000/,iseed/1/,nrun/100/,nhist/33*0/,p/0.49/
print *, L, maxstep, iseed, nrun
ibm=2*iseed-1
fact=L2/2147483648.0d0
ip=(2*p-1)*2147483648.0d0
neighb(0)= 1
neighb(1)=-1
neighb(2)= L
neighb(3)=-L
icountu=0
icountd=0
icount0=0
do 4 irun=1,nrun
do 1 i=1, Ls
ibm=ibm*16807
is(i)=-1
1 if(ibm.lt.ip) is(i)=1
do 2 itime=1,maxstep
m=0
do 3 k=2*L+1,L2+2*L
m=m+is(k)
5 ibm=ibm*16807
if(ibm.lt.0) ibm=(ibm+2147483647)+1
i=2*L+1+fact*ibm
if(i.le.2*L.or.i.gt.L2+2*L) goto 5
ibm=ibm*65539
j=i+neighb(ishft(ibm,-30))
ici=is(i)
if(ici.eq.is(j)) then
is(i-1 )=ici
is(i-L )=ici
is(i+L )=ici
is(i+1 )=ici
is(j-1 )=ici
is(j-L )=ici
is(j+L )=ici
is(j+1 )=ici
endif
3 continue
if(iabs(m).eq.L2) goto 6
c do 9 i=1,2*L
c is(i)=is(L2+i)
c9 is(L2+2*L+i)=is(2*L+i)
2 continue
print *, ' error, itime =', itime
icount0=icount0+1
6 ibin=alog(float(itime))/0.69315
nhist(ibin)=nhist(ibin)+1
if(m.eq.L2) icountu=icountu+1
if(m.eq.-L2)icountd=icountd+1
4 continue
do 7 ibin=1,32
7 if(nhist(ibin).ne.0) print *, 2**ibin, nhist(ibin)
print *, p, icountu, icountd, icount0
stop
end
BERNARDES, A.T., U.M.S. Costa, A.D. Araujo, and D. Stauffer, Int. J. Mod. Phys. C 12, 159 (2001);
BERNARDES,A. T., D. Stauffer and J. Kertész, Eur. Phys. J. B, in press (2002).
CHANG, I., Int. J. Mod. Phys. C 12, No. 10 (2001)
DEFFUANT, G., D. Neau, F. Amblard and G. Weisbuch, Adv. Complex Syst. 3, 87 (2000)
DITTNER, J.C., Nonlinear Analysis 47, 4615 (2001).
ELGAZZAR, A.S., Int. J. Mod. Phys. C 12, 1537 (2001)
HOLYST, J. A., K. Kacperski and F. Schweitzer, in Annual Reviews of Computational Physics IX, p.275, World Scientific, Singapore 2001.
MOREIRA, A.A., J.S. Andrade Jr. and D. Stauffer, Int. J. Mod. Phys. C 12, 39 (2001)
OCHROMBEL René, Int. J. Mod. Phys. C 12, 1091 (2001)
SPIRIN, V., P.L. Krapivsky and S.Redner, Phys. Rev. E 63, 036118 (2001)
SCHNEIDER, J., Int. J. Mod. Phys. C 13, to be submitted
SCHWEITZER , F. (ed.) Self-Organization of Complex Structures: From Individual to Collective Dynamics, Gordon and Breach, Amsterdam 1997.
STAUFFER, D., A.O. Sousa and S. Moss de Oliveira, Int. J. Mod. Phys. C 11, 1239 (2000)
STAUFFER, D., Int. J. Mod. Phys. C 13, No. 3 (2002)
SZNAJD-WERON, K. and J. Sznajd, Int. J. Mod. Phys. C 11, 1157 (2000)
SZNAJD-WERON, K. and R. Weron, Int. J. Mod. Phys. C 13, 115 (2002)
WEIDLICH, W. Sociodynamics; A Systematic Approach to Mathematical Modelling in the Social Sciences. Harwood Academic Publishers, 2000
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 2002