Volker Müller-Benedict (2002)
Xenophobia and Social Closure: A Development of a Model from Coleman
Journal of Artificial Societies and Social Simulation
vol. 5, no. 1
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/5/1/2.html>
Received: 29-Apr-2001 Accepted: 29-Nov-2001 Published: 31-Jan-2002
 Abstract
Abstract| Table 1: Person A's reactions when he/she encounters Person B (C = cooperation, D = defection) | |||||
| Person-B is | Person-A's previous move | Person-B reacted with | Person-A's move will be | ||
| n-2 | n-1 | n | |||
| 1 | a foreigner | - | - | => | D |
| 2 | a new acquaintance | - | C | => | C |
| 3 | a new acquaintance | - | D | => | D |
| 4 | an old acquaintance | C | C | => | C |
| 5 | an old acquaintance | C | D | => | D |
| 6 | an old acquaintance | D | C | => | C |
| 7 | an old acquaintance | D | D | => | C |
| (Coleman 1992:Table 7.2) | |||||
|
|
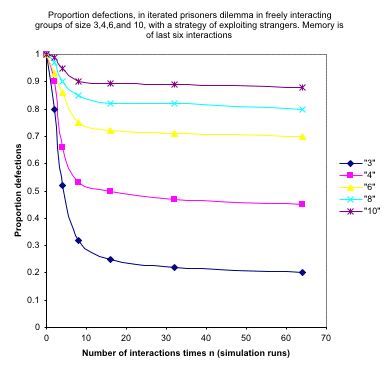
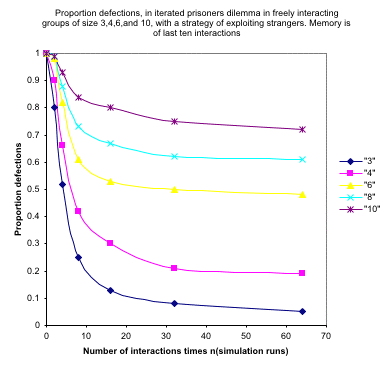
| Figure 1. (after Coleman 1992: Figures 7.2, 7.3) |
|
|
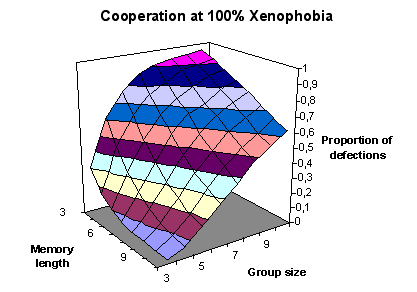
|
| Figure 2. Cooperation (measured by the proportion of defections) at 100 per cent xenophobia - variables: group size and memory length |
|
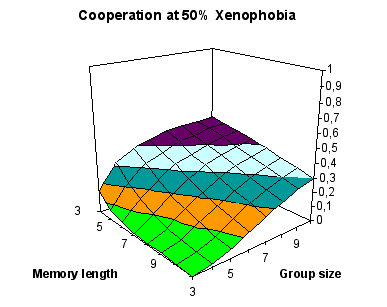
| Figure 3. Cooperation (measured by the proportion of defections) at 50 per cent xenophobia - variables: group size and memory length |
|
|
This proportionality explains the corresponding halving of the graphic.
|
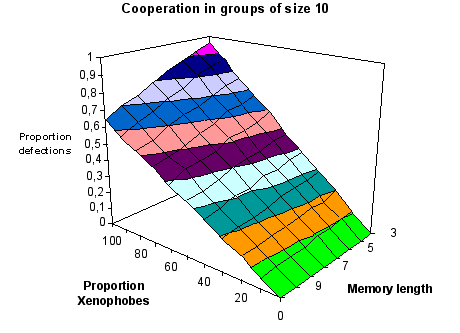
| Figure 4. The proportion of defections in groups of size 10 - variables: memory length and the proportion of xenophobes |
Taking 3 parameters into consideration allows us to make the following conclusion: There is very little cooperative behaviour in large groups when the majority of group members are not co-operators from the start.
| Axelrod | Coleman | ||||
| B Coop | B Def | B Coop | B Def | ||
| A Coop | 3, 3 | 0, 5 | A Coop | 0, 0 | -2, 1 |
| A Def | 5, 0 | 1, 1 | A Def | 1, -2 | -1, -1 |
|
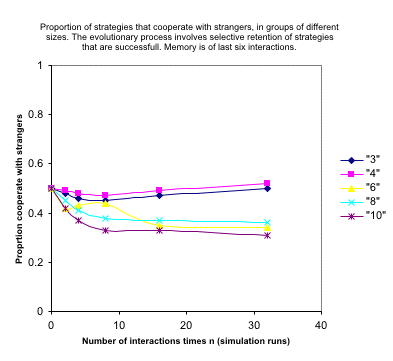
| Figure 5. (after Coleman 1992: figure 7.5) |
|
| Figure 6. Long-term proportion of co-operators when the starting proportion of xenophobes is 50 per cent and a strategy change is possible after 6 interactions. The values shown at memory length 6 in this graph represent the ending values of the curves in figure 5. |
Counterintuitive in this case is that memory length does not appear to play a large role in determining the long-term proportion of co-operators and that the proportion of co-operators is subject to strong chance fluctuations.
|
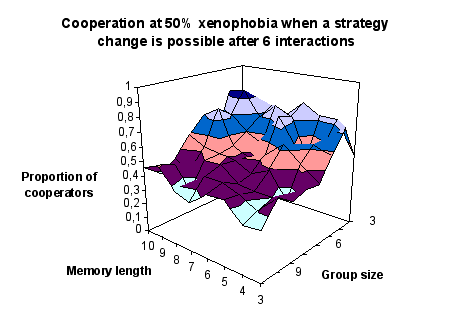
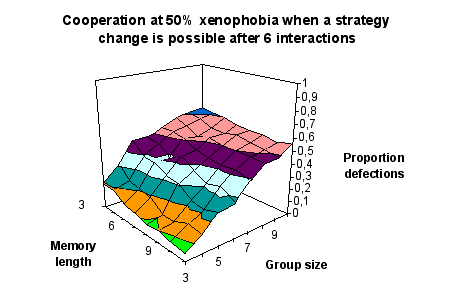
| Figure 7. Cooperation (measured by the proportion of defections) when the proportion of xenophobes is 50 per cent and a strategy change is possible after 6 interactions |
Here again we see the influence of memory length but only in smaller groups. In larger groups the variable memory length leads to completely counterintuitive results - when an increasing number of interactions are remembered, the proportion of defections climbs and remains above 50 per cent. But chance fluctuations appear to be at work here as well.
|
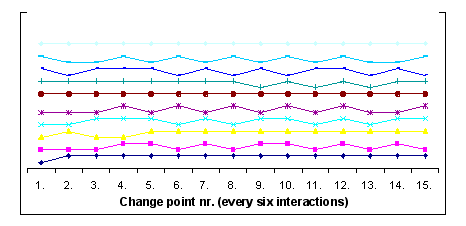
| Figure 8. A single run of the changes in behaviour towards foreigners - starting conditions: group size 10, memory length 10, starting proportion of xenophobes 50 per cent, and strategy change possible after every sixth interaction. The strategy selected is indicated in the following manner, low point = cooperate, high point = defect |
|
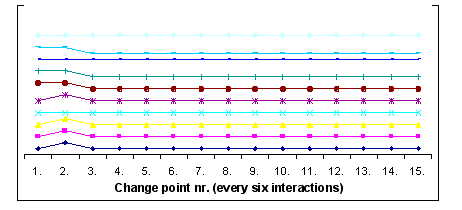
| Figure 9. Changes in behaviour towards foreigners during another single run when starting conditions are the same as in figure 8 |

|
| Figure 10. Cooperation in groups of size 10 with memory length 6 - variables: the starting proportion of xenophobes and the number of interactions till a strategy change can take place |
|
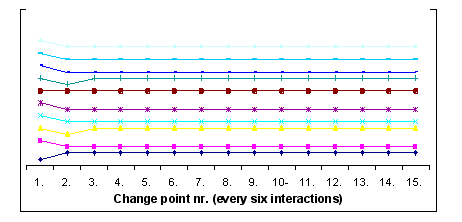
| Figure 11. Changes in behaviour towards foreigners during a single run - starting conditions are the same as in Figure 8 but with a starting proportion of xenophobes 90 per cent, strategy change possible after 6 interactions |
The conditions in Figure 11 are the same as in Figures 8 and 9, but in this case the proportion of xenophobes is 90 per cent. At the beginning the high level of xenophobia leads to low payoffs and a dramatic number of people switch to strategies of cooperation. As a result of the mechanism described above, these strategy changes stabilize after just a few more rounds till the xenophobes account for only 40 per cent of the population, which means that there is a 50 per cent reduction in the proportion of xenophobes (from 90 per cent to 40 per cent xenophobes). Therefore the long-term developments in this system tend towards the same proportion of xenophobes that is produced when strategy changes are not possible and the proportion of xenophobes is fixed at 40 per cent.
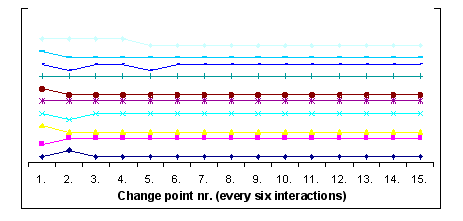
|
| Figure 12. Changes in behaviour towards foreigners during a single run with the same starting conditions as in Figure 8, but in this cast the starting proportion of xenophobes is 80 per cent |
2 For other reasons why a "demand for norms" comes into being when a decision must be made to cooperate or defect see Coleman (1986, 1992, 1990: chap. 10).
3"Suppose further that each animal can recognize individuals it has already interacted with and can remember salient aspects of their interaction, such as whether the other has usually cooperated" (Axelrod 1984:49)
4"So long as the expected time to the next interaction with a particular other is far into the future (as it will be in large populations Axelrod envisions), and so long as there is discounting of the future payoffs, a defect strategy will escape sanctions and will dominate all others." (Coleman 1986:66)
5 I hope to have thus acted on Coleman's observation that "Further work on the emergence of norms clearly appears profitable" (Coleman 1986:83).
6 For a discussion of the theoretical implications of this modelling (e.g. Axelrod and Hamilton 1981, Maynard Smith and Price 1973) consider the corresponding sections in Coleman (1992, 1990).
7 For a discussion of the advantages and disadvantages of using this game to model the evolution of cooperation see Coleman 1992:254f. Because of its simplicity (the exclusion of externalities which affect third parties and the fact that there are only two possible manners of behaviour) it is most certainly "a useful starting point" (256).
8 The group size N is based on the idea of "neighbourhood" and "embededness" in other models (Macy and Skvoretz 1998:655)
9 The memory length can thus be compared with Axelrod's "shadow of the future" and the accompanying discount-Parameter alfa. Hegselmann refers to (1-alfa) as the "degree of anonymity" (anonymisierungsgrad) in the society (Hegselmann 1992:187). The smaller the alfa and the shadow of the future, the more likely it is that the next interaction will be with a "foreigner". Memory length also plays a role in strategy-models based on genetic algorithms. When, for example, one can remember an opponent's last three moves, there are 215 possible strategies (Lomborg 1996:284). But in Lomborg's model all potential opponents are recognized, a fact which contradicts the intuitively limited nature of memory.
10 Another way of allowing the social structure to have an effect would be to use a model in which the division of the social structure is already set - a closely connected network (honeycombs) of neighbours for example (Axelrod 1984, Hegselmann 1996, Liebrand and Messick 1996).
11 Axelrod refers to this move as "contrition" (Axelrod 1997:37). Especially when noise is present, this strategy is advantageous. The effect of noise is comparable to the presence of foreigners.
12 This is of course only the description of a minimal strategy and other strategies, especially long-term strategies, are also plausible. But this minimal strategy is nonetheless intuitively plausible and, as far as profits are concerned, Axelrod's results demonstrate that this strategy is ideal in the long-term.
13The simulation program and its description are available at the author's internet-site: http://mzs.sowi.uni-goettingen.de/mitarbeitende/mueller-benedict/benedict.shtml or http://mzs.sowi.uni-goettingen.de/downloads/software/software.shtml
14 In this phase of the fixed strategy scenario the exact values of the payoffs in a prisoner's-dilemma situation are still unimportant; it is only important to know that cooperation leads to the highest payoff values.
15 Coleman (1990: 241f., 325f.) discusses a number of ways that sanctions can be established in order to maintain cooperation.
16 See as well figures 4.1 - 4.5 in Coleman ( 1986:76-80)
17 In 1986 Coleman concludes: "it turns out that the evolving system and the non-evolving system are scarcely distinguishable". In 1992 he presents an example calculation in which he assesses the long-term payoffs of all possible strategies when the group size is four. This calculation shows that it is plausible that the developments in this system will tend towards cooperation in the long run. But this assessment was only made for a single group size.
18 The nominator is the inverse of the payoff value and the denominator is the number of meetings in this round. The total number of meetings is the sum of all denominators. But, because of the randomly generated pairings of people, in which people sometimes meet themselves (encounters which do not count), this value doesn't equal 60.
19 In this paper a system will be defined as "self-organized" when the long-term end-state is unpredictable and is not determined by starting conditions. Such systems are, for example, chaotic systems or systems that have bifurcation points.
AXELROD, ROBERT 1984: The Evolution of Cooperation. New York: Basic Books
AXELROD, ROBERT 1997: The complexity of cooperation: agent-based models of competition an cooperation. Princeton: University Press
COLEMAN, JAMES S. 1986: Social Structure and the Emergence of Norms among Rational Actors. p. 55-85 in: DIEKMANN, ANDREAS and MITTER, PETER: Paradoxical Effects of Social Behaviour. Essays in Honor of Anatol Rapoport. Heidelberg:Physica 1986
COLEMAN, JAMES S. 1990: Foundations of Social Theory. Belknapp
COLEMAN, JAMES S. 1992: Norm-Generating Structures. p. 250-273 in: COOK, KAREN S. and LEVI, MARGRET: The Limits of Rationality. Chicago:University Press 1992
HAUSKEN, K. 2000: Cooperation and between-group competition. Journal of Economic Behaviour & Organization 42:417-425
HEGSELMANN, RAINER 1996: Cellular Automata in the Social Sciences. Perspectives, Restrictions, Artefacts. P. 209-234 in: HEGSELMANN, RAINER, Mueller, ULRICH and TROTZSCH, KLAUS G: (eds.): Modelling and Simulation in he Social Sciences from the Philosophy of Science Point of View. Dordrecht:Kluwer 1996
HEGSELMANN, RAINER 1992: Moralität im iterierten Gefangenen-Dilemma. p. 183-190 in HOLLIS, MARTIN and VOSSENKUHL, WILHELM (eds.): Moralische Entscheidung und rationale Wahl. München:Oldenbourg
HOBBES, THOMAS 1950 [1651]: Leviathan. New York: Dutton
HOFFMANN, R. 2000: Twenty Years on: The Evoluation of Cooperation Revisited. Journal of Artificial Societies and Social Simulation, vol 3, no. 2 <http://www.soc.sourrey.ac.uk/JASSS/3/2/forum/1.html >
LIEBRAND, W. and MESSNICK, DAVID: Computer Simulations of sustainable cooperation in social Dilemmas. p. 235-248 in: HEGSELMANN, RAINER, Mueller, ULRICH and TROTZSCH, KLAUS G: (eds.): Modelling and Simulation in he Social Sciences from the Philosophy of Science Point of View. Dordrecht:Kluwer 1996
LOMBORG,, B. 1996: Nucleus and Shield: The Evolution of Social Structure in the Iterated Prisoner's Dilemma. American Sociological Review 61:287-301
MACY, M., SKVORETZ, J. 1998: The Evolution of Trust and Cooperation Between Strangers: A Computational Model. American Sociological Review 63:638-660
MAYNARD SMITH, JOHN and PRICE, G. R. 1973: The logic of animal conflict. Nature 246:15-18
ORBELL, J., ZENG, L., MULFORD, M. 1996: Individual Experience and The Fragmentations od Societies. American Sociological Review 61:1018-1032
RAPOPORT, ANATOL and CHAMMAH, ALBERT M 1965: Prisoners Dilemma. Ann Arbor:University Press
ROUSSEAU, JACQUES 1950 [1756]: The Social Contract. New York:Dutton
VOGT, C. 2000: The Evolution of Cooperation in Prisoner's Dilemma with an Endogenous Learning Mutant. Journal of Economic Behaviour & Organization 42:347-373
WEBER, MAX 1976 [1925] : Wirtschaft und Gesellschaft . Tübingen:Mohr
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2002]