Felix Flentge, Daniel Polani and Thomas Uthmann (2001)
Modelling the Emergence of Possession Norms using Memes
Journal of Artificial Societies and Social Simulation
vol. 4, no. 4
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/4/4/3.html>
Received: 30-Mar-01
Accepted: 30-Sep-01
Published: 31-Oct-01
 Abstract
Abstract
![]() Introduction
Introduction
 Previous Work
Previous Work
 Social Norms and Memes
Social Norms and Memes
 The Model
The Model
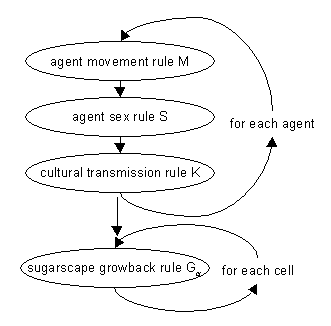
|
| Figure 1: Structure of a simulation step |
| Sugarscape Growback Rule Gα In each simulation step, the sugar content of a cell grows by α units until it reaches the maximum sugar capacity of the cell. α is an integer. |
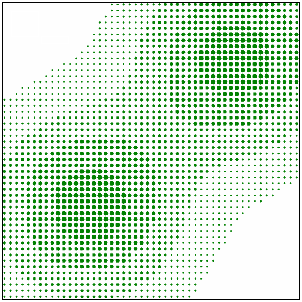
|
| Figure 2: The sugarscape landscape. The size of the dots is proportional to the sugar capacity of the cells. |
Agent Movement Rule M
|
Agent Sex Rule S
|
Cultural Transmission Rule K
|
Movement Rule MS
|
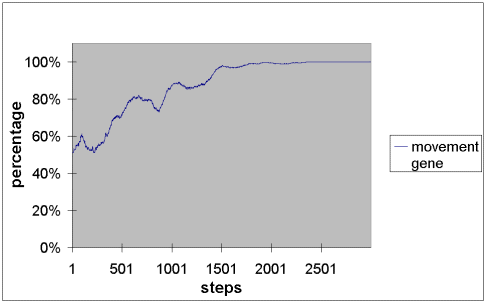
|
| Figure 3: The portion of agents with the movement gene. Agents with the gene perform rule MS, others rule M. Rules S and G1 are active, vision range and metabolism range from one to four. |
Cultural Transmission Rule K+
|
 Results
Results
| parameter | range | meaning | |
| initial sugar level | 50-100 | the amount of sugar the agents of the first generation get at birth; the following generations inherit their initial sugar from their parents | |
| maximum age | 60-100 | the maximum number of simulation steps an agent lives; he may starve earlier if he does not collect enough sugar; children inherit the maximum age from one of their parents | |
| male fertility start | 12-15 | the number of the simulation steps when the male/female fertility starts/ends; children inherit the fertility range from the parent with the same sex | |
| male fertility end | 50- 60 | ||
| female fertility start | 12-15 | ||
| female fertility end | 40-50 | ||
| number of memes | 11 | the number of memes influence the probability for each single meme to be changed through cultural transmission; in our model only two memes have a special meaning |
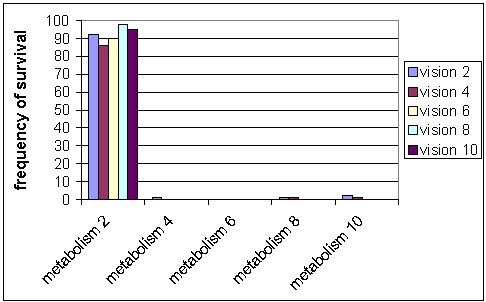
|
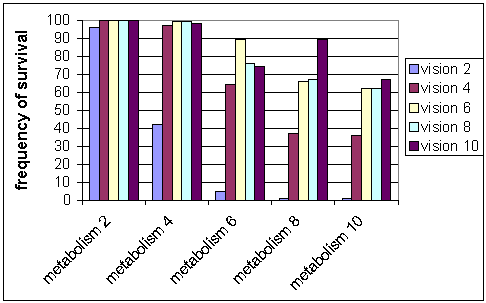
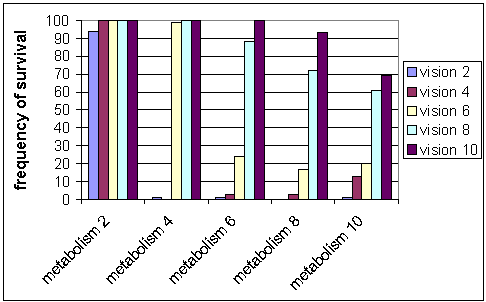
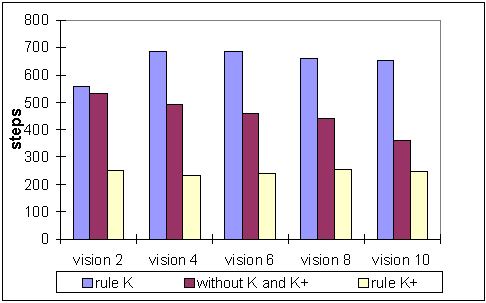
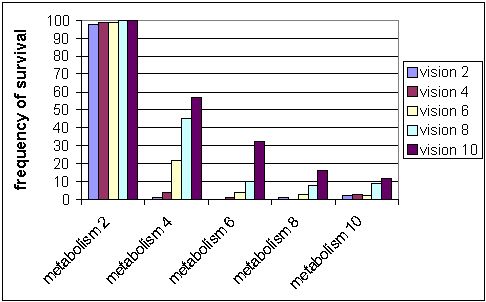
| Figure 4: Frequency of survival without possession meme. The figure shows that number of the runs in which the agent population survived 2000 steps versus different metabolism rates and vision ranges |
|
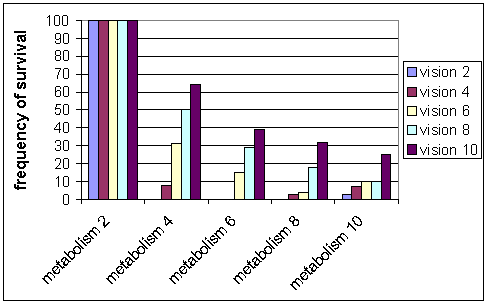
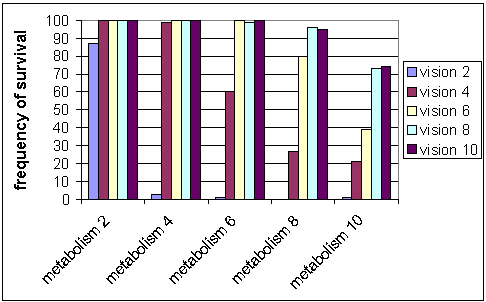
| Figure 5: Frequency of survival with possession meme |
|
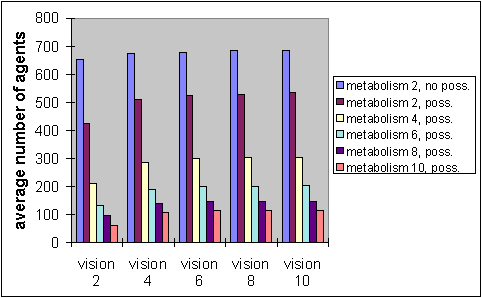
| Figure 6: Average number of agents in simulation runs with (poss.) and without (no poss.) meme and different vision ranges |
|
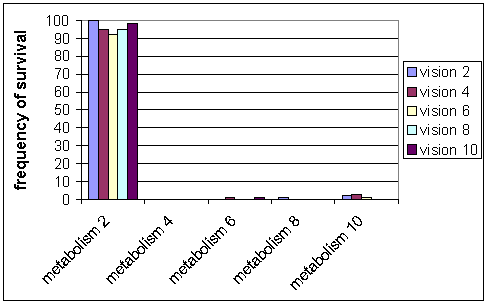
| Figure 7: Frequency of survival with active possession meme in 50% of the initial agent population |
|
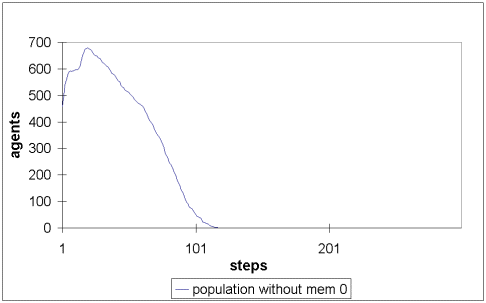
| Figure 8: Population growth without possession meme, a metabolism of four and a vision range of six |
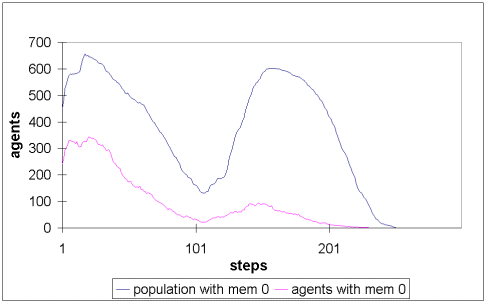 |
| Figure 9: Total population size (higher curve) and number of agents with possession meme (lower curve), metabolism four and vision range six |
|
| Figure 10: Frequency of survival with 50% possession meme, 100% sanction meme and a punishment of four |
|
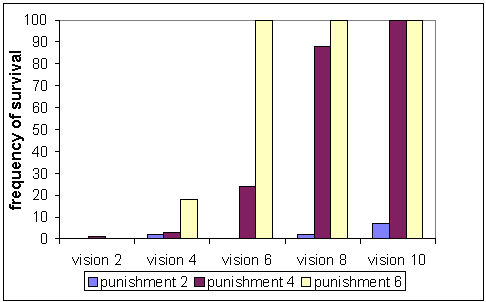
| Figure 11: Frequency of survival with metabolism six, vision range reaches from two to ten, 50% possession meme, 100% sanction meme and various punishments |
|
| Figure 12: Frequency of survival with 50% possession meme, 50% sanction meme, punishment twelve and costs of four |
|
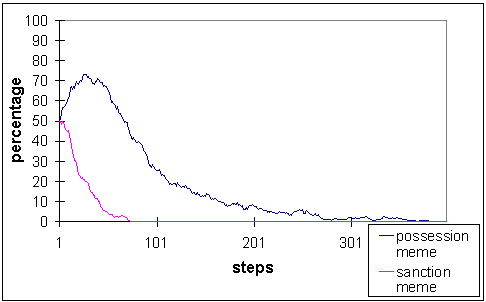
| Figure 13: Percentage of the possession meme and the sanction meme with costs four, metabolism four, and a vision range of six |
Role of the Memes
|
| Figure 14: Average time until the possession meme disappears with metabolism two and 50% possession meme at the beginning of the run |
|
| Figure 15: Frequency of survival without cultural transmission with 50% possession meme, 100% sanction meme and a punishment of four |
|
| Figure 16: Frequency of survival without cultural transmission with 50% possession meme, 50% sanction meme, punishment twelve and costs of four |
 Conclusion
Conclusion
 Notes
Notes
Executables (Win 95/98/NT), source code (Borland Delphi 4) and tables of all our experiments are accessible via <http://www.Informatik.Uni-Mainz.DE/~flentge/norm-sim_eng.html>
AXELROD, R (1997) "Advancing the Art of Simulation in the Social Science". In Conte R, Hegselmann R and Terna P (eds.) Simulating Social Phenomena. Berlin: Springer.
CASTELFRANCHI, C, CONTE, R and PAOLUCCI, M (1998) Normative reputation and the costs of compliance. In Journal of Artificial Societies and Social Simulation, vol. 1, no. 3, <https://www.jasss.org/1/3/3.html>.
COLEMAN, J S (1986/87) The Emergence of Norms in Varying Social Structures. In Angewandte Sozialforschung, Jg. 14,1 , 1986/87. pp. 17-30.
COLEMAN, J S (1990) Foundations of Social Theory. Cambridge, MA: The Belknap Press of Harvard University Press.
CONTE, R and CASTELFRANCHI, C (1995) "Understanding the functions of norms in social groups through simulation". In Gilbert N and Conte R (Eds.), Artificial Societies. The computer simulation of social life. London: UCL Press.
DAWKINS, R (1976) The Selfish Gene. Oxford: Oxford University Press.
EPSTEIN J M and AXTELL R (1996) Growing Artificial Societies. Cambridge, MA: MIT Press.
LATANÉ B (1996) "Dynamic Social Impact. Robust Predictions from Simple Theory" In Hegselmann R, Mueller U and Troitzsch K (Eds.), Modelling And Simulation In The Social Science From The Philosophy Of Science Point Of View. Dordrecht: Kluwer.
NOWAK A and LATANE B (1994) "Simulating the emergence of social order from individual behaviour". In Gilbert N and Doran J (Eds.), Simulating Societies. The computer simulation of social phenomena. London: UCL Press.
OPP, K (1983) Die Entstehung sozialer Normen. Tübingen: Mohr.
SAAM, N J and HARRER, A (1999) Simulating Norms, Social Inequality, and Functional Change in Artificial Societies. In Journal of Artificial Societies and Social Simulation, vol. 2, no. 1, <https://www.jasss.org/2/1/2.html>.
SCHÄFERS, B (1986) Grundbegriffe der Soziologie, Opladen: Leske + Budrich.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2001]