When two large groups of people meet in the same space, many outcomes are possible, depending on the types of groups and the occasion. These outcomes may range from a peaceful mingling of the two groups to the occurrence of fights and riots. Because the group processes leading to these outcomes are difficult to study experimentally, we developed a multi-agent simulation model in which the approach-avoidance conflict has been formalised in simulated actors. We worked with three different kinds of agents: hardcore, hangers-on and bystanders, the difference between them consisting in the frequency with which they scan their surroundings. Data on clustering, and 'fights' are presented for 80 simulation runs, in which group size, size symmetry and group composition were varied. The conclusions are that fights especially happen in asymmetrical large groups with relatively large proportions of hardcore members. Moreover, it appears that it are especially the hardcore group members and the hangers-on that attack other agents, whereas bystanders are victimised. The paper ends with a discussion on the validity of these findings, leading us to conclude that basic aspects of rioting behaviour are quite realistically represented in our simulation model.

Keywords:

Approach-avoidance; Conflict; Crowds

Introduction

1.1

The behaviour of people in crowd situations is a fascinating subject: crowds can be very calm but also rise to frenzy, they can lead to joy but also to sorrow, they can form a great subject for conversation but also for serious study. Empirical research on crowds is mostly done through observation, and thus offers little opportunity for causal analysis. Simulation is a technique that more and more offers exciting possibilities, as some form of experimenting with the dynamics of crowd behaviour becomes possible. The present paper aims at applying some recent innovations in computer simulations to the field of crowd behaviour. We will present some results of simulations of a special type of crowd situations, namely situations in which two relatively large groups of people, belonging to two different parties, can freely move about in a relatively large but bounded space. Instances of these types of crowd situations can be found in demonstrations, where partisans of two parties meet on a town square or in sports situations where supporters of two teams meet near the stadium. Mostly this type of situation gives little rise to problems, but under certain circumstances the situation can evolve into a riot. We aim to identify the working of some of the factors that precipitate riotous behaviour.

1.2

It is quite a common idea that people not only behave differently in crowd situations, but that they undergo some temporary personality change when they form part of a crowd. This idea is quite old and was stated in its most pure form by Gustave LeBon in his influential book La psychologie des foules (1896). Recently this idea of a transformation of human characteristics in a crowd has been heavily criticised. Modern authors like Reicher (1987), McPhail (1991) or Adang (1998) argue that the idea of transformation was based on biased intuitive insights and on equally biased eyewitness reports but has never been proved empirically. Only quite recently, mainly through the development of better observation techniques, empirical research on crowds has become feasible. From this research it becomes more and more clear that crowd behaviour is essentially normal behaviour, albeit in extraordinary circumstances. The only thing that changes when the situation becomes extraordinary is that the participants undergo mood changes not essentially different from those in normal circumstances.

1.3

The question then rises as to what constitutes these special circumstances. Most writers in the field of mass- or crowd- psychology agree that the most discriminating property of crowd situations is that normal cultural rules, norms and organisation forms cease to be applicable (e.g. Milgram & Toch, 1969, Marx & McAdam, 1994). For instance in a panic situation the normal rule of waiting for your turn, and the concomitant organisation form of the queue, are violated and thus become obsolete. New rules and organisational forms then have to be found, but which? Another example is formed by riotous mobs. Normally when many people are gathered in one place, rules like minding your own business, controlling your emotions and being polite are in operation. This results in loose organisational forms like the shopping public or the viewing or listening public. Once these rules and organisational forms get lost new ones have to be found. We can thus conclude that when cultural norms and organisation forms cease to apply, people will fall back on simpler rules, rules that can be understood by all present without instruction or too much cultural knowledge.

1.4

In this paper we will use essentially three very simple rules that govern the behaviour of the actors: a restricted view-rule, an approach-avoidance-rule and a mood-rule. The restricted view- rule implies that actors in crowd situations are only able to monitor the behaviour of other actors that are quite nearby. The approach-avoidance rule implies that actors are motivated to approach a specific set of co-actors and to avoid a specific set of others. The mood-rule implies that the approach avoidance tendencies are susceptible to mood.

1.5

Another finding of modern crowd research that is at odds with traditional ideas is that crowds are not uniform. For instance Adang (1998) found that some 90 percent of people present in a riot situation are quite calm and only fulfil the role of spectator. The behaviour of the minority that is active in riot situations is moreover not so indiscriminately brutal and thoughtless as LeBon suggested. Reicher (1987) for instance reports that aggression and demolition in a riot situation was quite selectively aimed at outsiders and their property, such as government officials and public buildings. It has also been found that in crowd situations those present are not acting as one group consisting of uniform parts, but that crowds consist of small groupings of friends or acquaintances. Only within these groups a certain uniformity may be expected. We therefore discriminate between three types of actors: Hardcore members, Hangers-on and Spectators.

Simulation of Crowd Behaviour

2.1

Simulation is a young and rapidly growing field in the social sciences (e.g., Axelrod, 1997, pp. 21). The idea that social processes could be simulated by substituting all kinds of parameter values in a mathematical model of social mechanisms was originally developed by economists and mathematicians. In the last decades there has been a rapid increase of the use of computer modelling in psychology. Many social scientists and computer programmers are fascinated by the growing possibilities computers offer for modelling parts of the world including aspects of individual human behaviour. On the basis of such models it more and more becomes possible to quite realistically simulate the total behaviour of a target system on the macro level. The simplest form of crowd simulation implies that we translate some essential crowd mechanisms in a mathematical model of the crowd, and experiment with different settings of the model, such as group size, general mood and time of the day. The group-members are essentially seen as identical and interchangeable. The model is then fed in a computer and the effect of changing parameters on outcomes of crowd behaviour can be obtained by computing the values for specifiable dependent variables.

2.2

The parameters used in the earlier models of mass behaviour were defined on the macro-level, but it is obvious that in reality they could work only when they influence the behaviour of individual group-members, i.e. on the micro-level. Many researchers therefore acknowledged that mass or crowd behaviour should be understood from motives at the micro-level. A starting point for this kind of modelling is found in Schelling's (1978) book: "Micromotives and macrobehavior". In this book, Schelling explores the behaviour characteristics of the individuals who comprise some social aggregate, together with the characteristics of the aggregate. For instance with regard to spatial behaviour, Schelling wrote on sorting and mixing in neighbourhoods, and illustrated this with exemplary calculations.

2.3

In the same spirit Granovetter (1978) developed a so called 'threshold model' of crowd behaviour. This class of models differs from the foregoing types of simulations in that way, that it is assumed that people differ regarding their individual motivation, e.g. their motivation to migrate, to adopt an innovation or to join in riotous behaviour. These different motivations were formalised as different thresholds to engage in the behaviour in question. The motivational factor is defined as some form of imitation or conformity. Thus people with a very low threshold do not need a behavioural example to engage in rioting (Granovetters definition of hard core members), others only start behaving actively if they see a certain percentage of the crowd engaged in rioting. Granovetter experimented with various distributions of thresholds to investigate crowd behaviour. Given an initial distribution of person characteristics, Granovetter's threshold-model is capable of estimating the chances of a riot to emerge and the number of people involved. Like in earlier models, several kinds of parameters could be introduced, such as the weather, number of police officers involved, size of city or relative size of certain groupings. Granovetter also tried to introduce friendship patterns between participants as a parameter, but this appeared rather difficult. Despite the greater sophistication of this model compared to earlier ones, it has some serious drawbacks.

2.4

A first problem is that in Granovetters model no real individuals are at work, but only the result of a certain distribution of individual properties is computed. He thus works with stochastic variables resembling individuals. Nevertheless he talks about individuals having trait-like thresholds. This implies that whatever the circumstances, the stochastic individual always will riot if his threshold value is reached. This clearly is an unrealistic statement. Second, in Granovetters model the crowd members are supposed to perceive the behaviour of all other members, and know exactly the percentage of others engaging in rioting behaviour. In our view an individual's knowledge on the behaviour of others in a crowd is local and not so statistically precise. Finally, in Granovetters model there is an operationalisation of when a person starts rioting, but not of when he stops. This may stem from Granovetter being mainly interested in the chances of a riot to happen. This approach thus implies that once an individual is engaged in rioting behaviour, he will never stop. This is of course in contradiction with empirical facts and will give us an overrated estimate of the number of rioters.

2.5

Very few studies address the spatial dimensions of social interaction. When one wants to study individual behaviour in crowds of people, the spatial dimension is of course very important. The spatial crowd simulations that have been developed are usually based on identical actors that are stable with respect to their behavioural rules. Some of these simulations pertain to flocking behaviour of animals (e.g., Reynolds, 1987; Tu & Terzopoulos, 1994). A few are concerned with the motion of human crowds (Yin, 1997; Bouvier, 1997; Musse & Thalman, 1997; Helbing & Vicsek, 1999; Helbing, Farkas & Vicsek, 2000). Whereas these spatially oriented models are very elaborate concerning motion and collision avoidance, they are relatively poor regarding the psychological motives that guide the agents' behaviour

The Multi-agent Approach

2.6

In the late seventies and early eighties the multi-agent simulation was hardly being used because of the lack of fast computers. The appearance of modern personal computers on the desks of many researchers provided the means for a fast development of computer models, especially multi-agent modelling. While earlier computer simulation can be considered as a single calculus with relevant parameters that could be set at different values, multi-agent simulations can be thought of as consisting of as many calculuses as there are agents. Thus, while classical, single calculus simulation is suited for the top-down or macro-approach, for a bottom-up or micro-approach of crowd simulation a multi-agent modelling approach is much more appropriate.

2.7

Agents influence each other, but they operate as individuals. In this study individual crowd members are represented as agents. We assume that three characteristics at the individual level are essential to model the behaviour of crowds. Firstly, any group of people consists of different individuals in different psychological states. This implies that different people may behave differently in a specific situation. Second, these individuals do not know nor perceive all other individuals. In a crowd, one is more likely to react on the behaviour of one's neighbours, because these people are the most visible. Hence, we assume that people interact on a local scale. Thirdly, the individuals have some degree of freedom regarding what behaviour to perform. It is assumed that the tendency to approach or to avoid is a very fundamental behavioural characteristic. The behaviour of our agents is moreover not purely deterministic, but may show random variations.

2.8

An agent is a being or a thing possessing characteristics and a calculus for converting inputs (information) from its environment, in accordance with these characteristics, in outputs (behaviour). These outputs then influence the environment and this again influences the behaviour of the agents. The values for a characteristic are not necessarily stable for each agent, but as the inputs change, the outputs can differ depending on the values for these characteristics of the agent combined with changes in the environment of the agent.

2.9

Agents also differ in the stability of their characteristics. In average crowd situations some 1% of those present will be hardcore members, unpredictable and active agents. Some 10% are hangers-on, being more predictable and less active. The bystanders thus form some 90% of those present, they mostly behave in a predictable and not very active way (Adang, 1998). We assume that the first type, the hard-core members, will tend to frequently and actively survey their surroundings, in order to detect favourable occasions for their actions. The second type of individuals, the hangers-on, is assumed to survey their surroundings less actively and frequently than the hardcore individuals. Finally the bystanders are people who are interested in what happens, but mainly as spectators. This type of agent is assumed not to be very active in scanning his surroundings for opportunities for action.

2.10

We intended to develop a crowd simulation that employed autonomous agents moving in cyberspace and equipped with psychological motives. We therefore combined a relatively simple model of agent orientation and movement with a simple behavioural model that describes the motivations of the agents. In developing the behavioural rules for these agents we had to find a balance between realism and simplicity. Formalising relevant behavioural theories into behavioural rules for the agents contributes to the realism of the simulation and thus the significance of the results obtained by using this method. In the method section we will describe the formalisation of the relevant behavioural theories into simple agent rules.

Conclusions for the Multi-agent Simulation of Crowd Behaviour

2.11

From the endeavours towards a taxonomy on factors relevant for understanding crowd behaviour, as yet no generally accepted consensus has emerged. Nevertheless, in making a simulation, one has to choose which kinds of crowd situation will be simulated, and which not. In our case we opted for situations in a delimited but sufficiently large square space. The duration (i.e. the number of 'cycles') of the simulations should be long enough for typical and rather stable patterns of behaviour to emerge. In the space maximally some hundreds of persons should be present. These persons should not be uniform in their habits or 'personality', thus we have three types of agents and each agent can be in a definable state. It is therefore necessary to equip the agents with some kind of leading emotion, like aggression. The persons should belong to a definable group. It should be possible to work with either one single, undivided group or with several parties. The groups or parties should initially be unorganised, and have no leader. The behaviour of the persons should be sensitive to the nearness of others agents and partly self- directed, partly directed by chance.

2.12

Moreover we made some assumptions on typical behaviour of people in crowded situations, based on quite normal behavioural rules. A first assumption is that normal everyday norms and forms of organisation lose to a certain extent their applicability, and thus the behaviour of the agents is based on personal on or emerging norms. The second was co-presence and a certain amount of interaction, especially in sub-groupings. Further a common behavioural tendency was supposed to be working on the agents. The agents were assumed to have a tendency to roam around within the limits of the crowd area (milling), and to be actively surveying their immediate surroundings. When the agents notice something of interest within the crowd perimeter, they are assumed to approach it until they are held up by some repelling factor (approach-avoidance conflict, Miller, 1944). The agents are assumed to be attracted by people who are similar to themselves, the members of parties thus will have the tendency to approach each other, and especially people they know. As they become then more and more surrounded by sympathetic individuals, or even acquaintances, people in the resulting clusters are assumed to gain in self assurance Hogg & Abrams, (1988). When the agents have gathered enough self-assurance they will gain in the tendency to approach members of the other party.

The Simulation Model of Crowd Behaviour

3.1

In the following sections we discuss the behavioural model that describes the rules of the individual agent. This model has been programmed by E. Baas and can be downloaded here. A large number of agents, all being equipped with this model, behave and interact with one another according to the rules of this behavioural model. They do so in a certain space and within a certain time span, so we first have to formalise the space-time environment in which the agents behave.

The Environment

3.2

The environment consists of cells each resembling a space of 1 square meter. Only one agent can occupy a cell at a given time. We constructed a square of 100 by 100 cells, the equivalent of a 10.000 square meter space. This square is a so-called island model, which means that the outer borders are closed. Hence, it is not possible for an agent to move from one border directly to the opposite border, as is sometimes seen in spatial simulations. Apart from the function of providing space for agent movement the cells have as yet no special characteristics.

The Time

3.3

One time step in the simulation-run resembles 1 second. Setting a simulation-run at 3600 time steps thus simulates the crowd behaviour during one hour. Because the agents can move one cell per time-step, their maximum speed is 1 m/sec. Except for the possibility of standing still, no variance in running speed has as yet been provided.

The Agents

3.4

The agents are equipped with an identity (being a specific type in a specific party), the ability to perceive their surroundings, an internal state and a set of behavioural rules. Moreover for every agent 15 specific party-members are defined as 'acquaintances'. The agent characteristics allow them to perform a limited number of behaviours: The standard rule is that each cycle they either randomly move, or move around the centre of the square one cell or stand still. The relative chances of each of these movements can be chosen for each simulation run. In the present simulations they were chosen as 0.50, 0.45, and 0.05. When the agent perceives other agents nearby the standard rule is abandoned: now the agent may approach agents belonging to his own party, with a predilection for acquaintances, approach agents belonging to the other party, or engage in a fight with agents of the other party. These behaviours essentially follow from the agents' perception of the environment and his internal state.

3.5

We distinguish between different types of agents: hardcore, hangers-on and bystanders. These different types of agents scan their environment with a different frequency. The hardcore members, scan every x time-steps, hangers-on, scan every 2*x time-steps, and bystanders, scan every 8*x time steps. In the present simulations the value of x was 10. For each of the two simulated groups we can define a proportion of hardcore members in the range of 1% to 33%. The hangers-on have a share of 2 times the hardcore percentage. The remaining agents are bystanders. These values are used as an independent variable in the present simulations.

3.6

While scanning the environment, the agents are not capable of perceiving the complete square. Their perception is limited to 20 cells in each dimension. Thus they are capable of scanning a field of 40 * 40 cells (a 40x40 Moore neighbourhood), provided that there is no border within 20 cells distance. The object of scanning activity is to determine how many agents of own and of other party are near, if there are any acquaintances, and in which direction they all are posited. This results in the determination of a direction for own majority, for acquaintances, and for other majority. The results of this scanning in terms of number affect the internal state of the agents. The internal state determines, together with the direction-results, the agent related movements.

3.7

The agents' internal state is called their 'aggression motivation', i.e. their tendency to approach or avoid and, in certain cases, their tendency to start a fight. This aggression motivation ranges from 0 to 30. For every agent it starts with the value 0. If in a scan a majority of own members is found that outnumbers the other party with at least 10 members, the aggression motivation will be raised by 1 point. If there is a majority of other party members that outnumbers the own party with at least ten members, it will decrease 1 point. When the observed difference between the size of the own party and the other party is less than 10 members, the aggression motivation will remain unchanged. When the aggression motivation is 15 or lower (avoid state), the agent will be motivated to go towards own party. If party members are around, it will move to the quadrant (in its scanning field) with the largest number of own party members. If no own party members are around, it will move according to the standard rule.

3.8

If the aggression motivation of an agent is above 15 (approach state), the agent is motivated to go towards the other party. The agent will move towards the quadrant with most members of the other party. The agent will also scan if he has direct contact with a member of the other party. If that is the case, and the aggression is above 25 (Aggressive state), it will engage in a 'fight' for 100 seconds. A fight in our case just means that the two agents are immobilised. After the fight the aggression motivation of the attacker will be reset to zero. In the case of direct contact and the aggression motivation being between 15 and 25 (Approach state), there is no immobilisation, but the agent will closely follow the other agent. If the agent does not perceive members of the other party, it will move according to the standard rule. The rules are organised in the behavioural model in Figure 1.

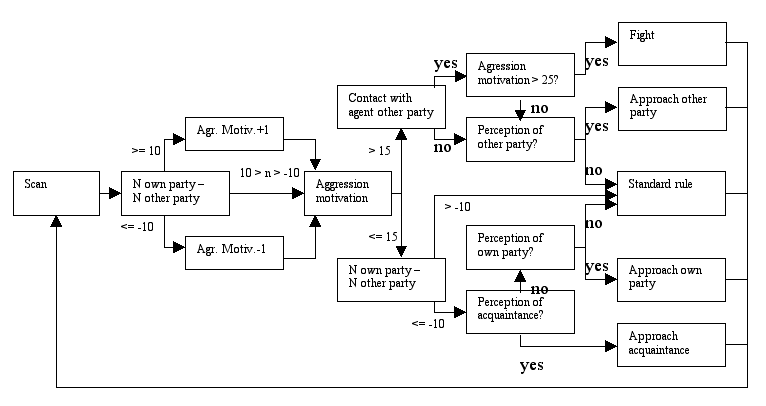
Figure 1. The behavioural model of the agents

.

Further Features of the Simulation Program

3.9

The program randomly places a specified number of agents in the square. The number of agents in both parties and the ratio between hardcore, hanger-ons and bystanders has been specified as an independent variable before running the model. Before running the model, the program automatically links agents to 15 other agents from the same party, which are then his acquaintances. The acquaintance relation is always bi-directional.

3.10

During the simulations the program copies the values for the state variables of all agents at every 20^th time step to an output- file, which can be used as input for statistical analyses. Moreover the program gives a real time visual representation of the movements of the agents. Through the use of different colours it is possible to identify the party membership and motivational state of each agent. The use of a rather elaborate shell structure offers easy possibilities for setting parameters and changing other settings, thus making the program flexible.

Design of the Simulation Experiments

3.11

In this paper we will report on the influence of three independent variables on several dependent ones. As independent variables we will use:

1. Size of the crowd,
2. Relative size of the parties, and
3. Proportion of hardcore individuals.

All three variables will be varied on two levels. The size of the crowd will be either 400 agents (being the maximum that the present simulation program can handle), or 100 agents. The relative size of the parties will be either symmetrical (.50/.50) or asymmetrical (.25/.75). The proportion of hardcore individuals will be either 1% of the party size, or 5%. When the proportion of hardcore individuals is 1%, the proportion of hangers-on is 2% and the remaining 97% are bystanders. When the proportion of hardcore individuals is 5%, the proportion of hangers- on is 10% and the remaining 85% are bystanders. If the percentage of hard-core and/or hangers-on results in a broken number of agents, the integer part of that number is used to define the number of agents. The number of bystanders is found by subtracting the number of hardcore and hanger-on agents from the total number of agents in the party. We thus get the 2*2*2 design presented in Table 1.

Table 1: Design of the study
	Large crowd (400)		Small crowd (100)
	HC = 1%	HC = 5%	HC = 1%	HC = 5%
Symmetrical	HC: 2/2 HO: 4/4 BY 194/194	HC: 10/10 HO: 20/20 BY: 170/170	HC: 1/1 HO: 2/2 BY: 47/47	HC: 3/3 HO: 6/6 BY: 41/41
Asymmetrical	HC: 1/3 HO: 2/6 BY: 97/291	HC: 5/15 HO: 10/30 BY: 85/255	HC: 0/0 HO: 0/1 BY: 25/74	HC: _ HO: 2/7 BY: 22/64
	In the table the numbers of each type of agents for each party are given. HC = Hardcore, HO = Hanger-on; BY = Bystander

3.12

Each simulation run involves 5400 time-steps, resembling 1.5 hours. Ten simulation runs have been performed for each experimental condition in the design, resulting in a total of 80 simulation runs. We have used a fixed value of 10 for x in all conditions, which implies that the hard-core agents scan their environment every 10 seconds, the hangers-on every 20 seconds, and the bystanders every 80 seconds.

3.13

The dependent variables in this study come in two main classes, space related and state related variables. Space variables can give insight in the clustering of agents and their relative positions. They also comprise the number of group members, acquaintances, and non-group members surrounding the agent. Space variables are important in that they can be seen as antecedents of crowd activity. State variables give insight in the motivation and the behaviour of the agents. They thus describe the most important aspects of crowd behaviour. The dependent variables will be reported in absolute numbers and as proportions of the total crowd and of each party. Moreover the data will be presented separately for the three kinds of agents: hardcore, hangers-on and bystanders.

3.14

The space variable we will specifically report on as a dependent variable is the clustering of agents. This is computed as the average number of party-members in the immediate environment of each agent. The immediate environment is defined as all cells at a distance of 3 or less. More formally this is the 7x7 Moore neighbourhood, consisting of the 48 cells surrounding the agent. The higher the numbers of own party-neighbours, the stronger the clustering will be. This measure does not directly indicate the number or sizes of clusters, but can be seen as a general indicator for clustering. For heuristic purposes we also computed the number of acquaintances in this neighbourhood.

3.15

The state variables are aimed at giving insight in the degree of aggression in the different conditions. We will present data giving insight in the number and proportions of agents in Approach state (15 < aggression motivation < 25) and Aggressive state (aggression motivation > 25). Again we will do this for both parties and for the three types of agents. As with the space variables we will present the data in the form of both tables and graphs.

Results

4.1

In this section we will essentially report quantitative data on our simulation runs, but we will also give some more subjective impressions derived from observing the runs as if they were real crowd phenomena. First we will present some results on the clustering of the agents. Following this, we will present some results concerning the fights that emerged in the different conditions.

Clustering of the own Group Members

4.2

Clustering is being defined as the grouping together of agents of the same party. In the next Figure 2 this clustering is exemplified for the large asymmetric crowd condition at t = 340. Here it can be seen that the agents that are in the minority (red) are clustering more than the green agents do. Moreover, it can be seen that in the red clusters a relative large proportion of the agents is blue, indicating agents in the approach stage. A few white agents can be seen, representing agents in the aggressive state.

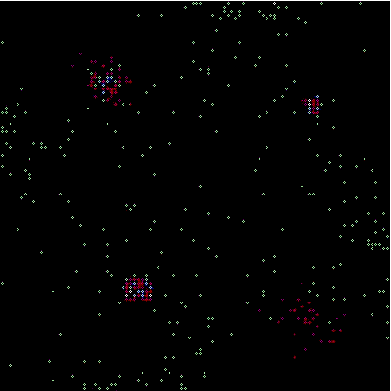
Figure 2. An example of clustering

4.3

Clustering of the own group is measured by counting the number of agents of the own party surrounding an agent up to distance 3 (a Moore environment consisting of 48 surrounding cells). Calculating the average for all agents of one party provides a clustering-index ranging from 0 (no clustering at all) to 48 (maximal clustering). In Figure 3 we show how this clustering-index evolves over time for the eight conditions.

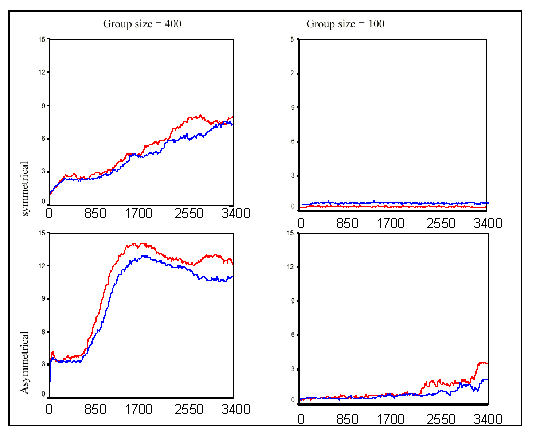
Figure 3. Number of group members at a distance of 3 or less. The blue line denotes the conditions with 1% hard-core, the red line the conditions with 5% hard-core. Note the smaller scale of the y-axis scale in the top right figure for reasons of visibility.

4.4

In the beginning (t=0), the clustering is necessarily very low because the agents are randomly distributed over the space. However, it can be seen that there are important differences between the conditions in the degree of clustering that occurs. Generally the tendency toward clustering is stronger as the crowd is larger. The clustering is also stronger when the parties are asymmetrical. As can be seen, this clustering emerges most strongly in the asymmetrical n=400 condition. Here, the condition with 1% hard-core members shows the strongest clustering. The condition with symmetrical groups and n=100 shows somewhat less clustering, the condition with asymmetric groups and n=100 shows little clustering, and the symmetrical groups with n=100 show no clustering at all. Logically, in the n=400 conditions more cells are filled with agents, and as a consequence the clustering is higher. In both asymmetrical conditions the clustering is higher than in the corresponding symmetrical group conditions. This effect is due to the fact that in asymmetrical groups the minority group agents start clustering because they generally do not 'like' being in an environment with a majority of other-party agents. This of course not only causes the minority group to start clustering, but also that the majority group will occupy the remaining space, which also causes the clustering-index to rise.

4.5

Most interestingly, in the asymmetrical n = 400 condition we observe that after a peak in the clustering around t = 2500, the clustering decreases somewhat. This effect is due to the fact that at that time the aggression-motivation of many agents has exceeded the critical level of 15. This implies that after t = 2500 more agents are motivated to approach agents of the other party, and to engage in a fight. Consequently the clustering index, although still being at a high value, show a small decrease.

Clustering with the Members of the other Group

4.6

The number of agents of the other party surrounding an agent up to distance 3 (a Moore environment consisting of 48 surrounding cells) are counted and aggregated over all agents. The resulting clustering-index in theory ranges form 0 (no clustering at all) to 48 (maximal clustering). In Figure 4 we show how this clustering-index evolves over time for the eight conditions.

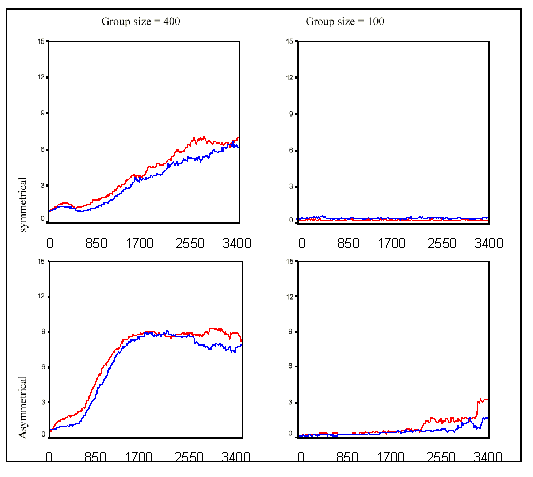
Figure 4. Number of non-group members around up to distance 3. The blue line denotes the conditions with 1% hard-core, the red line the conditions with 5% hard-core.

4.7

As can be observed, the clustering with other party agents is rather similar to the clustering with own party members (Figure 3). Especially in the asymmetrical n=400 condition this clustering is important. However, some small differences with Figure 3 can be observed. First, the clustering-index does not reach a value as high as for the own party members. For the asymmetric large crowds we observe the clustering index to rise from 3 to around 14, and for non-party members from around 1 to about 8. This implies that especially in the asymmetrical n=400 condition the agents cluster more with own party agents than with agents belonging to the other party.

4.8

A second difference is that the own-party clustering index rises earlier than the clustering index for the other-party. The peak for the own-party clustering index is at t ? 2500, whereas the peak for the other-party clustering is at t ? 3000. This difference indicates that the agents tend to cluster first with the own party-members. This clustering causes the aggression motivation to rise after some time, stimulating the agents to approach the other party members. Consequently, the clustering of the own-party member elicits some time later a clustering with other-party members.

Fighting with Members of the other Group

4.9

When the aggression motivation of the agents rises, they tend to approach the other party-members, causing a clustering with other-party members. We will not specifically report on the data for the approach state (15 < aggression motivation < 25), as these mirror the data on fights. When the aggression motivation exceeds the critical value of 25, the agent will attack other party members he encounters. In Table 2 the percentage of agents that is being caught up in a fight, either as an attacker or as a victim, is reported. In reading Table 2, the reader has to be aware that the totals of attacking and victimised agents in one cell of the design do not have to be equal. This is due to the fact that an agent might be victimised by two or more other agents, which yields two or more observations of attacking, but only one observation of victimising.

Table 2: Percentage of agents involved in fight
		Large crowd (400)				Small crowd (100)
		HC=1%		HC=5%		HC=1%		HC=5%
		Att.	Vict.	Att.	Vict.	Att.	Vict.	Att.	Vict.
Symmetrical	All HC HO BY	0.01 - - 0.01	0.01 - - 0.01	0.38 0.28 0.08 0.03	0.36 0.03 - 0.33	- - - -	- - - -	- - - -	- - - -
Asymmetrical	All HC HO BY	88.74 4.84 4.94 78.99	66.70 1.01 2.65 63.04	132.3 26.10 29.44 76.76	96.99 6.37 8.92 81.71	0.10 - - 0.10	0.10 - - 0.10	7.62 1.68 2.42 3.52	6.76 0.02 - 6.74
In the table the numbers of each type of agents for each party are given. HC = Hardcore, HO = Hangers-on, BY = By-standers; Att. = attacking agent, Vict. = victimised agent

4.10

In Table 2 we observe that in the n=100 symmetrical condition no agent attacks other agents, and as a consequence, no agent is being victimised. In the n=100 asymmetrical and the n=400 symmetrical conditions the percentage of attacking and victimised agents are also relatively low. Only in the asymmetrical n=400 condition a substantial percentage of agents is being caught up in a fight, either as an attacker or as a victim. Especially when the percentage of hard- core members is 5% many agents started attacking. In the latter condition we observe percentages of over 100%, clearly indicating that agents must have started attacking more than once.

4.11

To get a picture of how the fighting evolves over time, we present the number of fights (= number of victimised agents) per time-step in Figure 5. Because only in the n=400 asymmetrical condition a substantial number of fights take place, we present only the results for this condition.

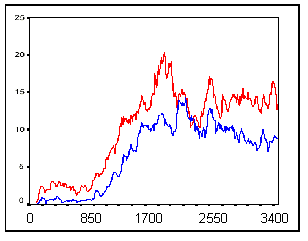
Figure 5. Number of fights started over time for the N=400 asymmetric condition. The blue line denotes the conditions with 1% hard-core, the red line the conditions with 5% hard-core.

4.12

As can be seen from Figure 5, the fighting in the n=400 asymmetrical condition starts rising at t ? 1500, and peaks at t ? 2800 for the 5% hard-core condition, and at t ? 3200 for the 1% hard-core condition. This difference can be explained as follows. The hard-core agents (and the hangers-on) scan their environment more frequently. This causes them to cluster faster with their party-members (see Figure 3) and to adjust their aggression motivation much faster than the bystanders. As a consequence, in the condition with a larger proportion of hard-core agents this faster clustering and more frequent scanning yield a faster rise in the aggression motivation. This causes that in the 5% hard-core condition the agents approach the other party-members earlier in time (Figure 3), and engage in fights more quickly (= earlier in time) and more frequently than in the condition with only 1% hard-core agents (Figure 5).

4.13

When we look at the statistics of fighting (Table 2), we observe that in the n = 400 asymmetrical condition, both the attacking agents and the victimised agents are usually bystanders. This is not very surprising, as they constitute the largest proportion of the crowd. However, the hard-core and hanger-on agents much more frequently attack other agents than that they are being victimised. This is due to the fact that their faster rise in aggression motivation causes them more often to initiate aggressive acts.

Discussion

5.1

As was stated in the introduction of this paper, there exist relatively few studies on the dynamics of crowd behaviour. These studies are all based on observational data, as it is virtually impossible to conduct experiments with large crowds. Whereas the observational data are very rich regarding the description of what happens in large crowds, they do not give us insight in the effects of specific conditions on what is happening. One of the main reasons for that is the difficulty to trace the behavioural processes of the many individuals in a crowd. In contrast, as has been demonstrated in this paper, the multi-agent modelling approach offers a research tool that allows for hypotheses testing on interactions between individual behavioural processes and crowd behaviour. Moreover, the model also allows for generating hypotheses. For example, dynamics that are being identified in the simulation model can guideline empirical studies of crowd behaviour.

5.2

In the multi-agent approach applied in the work presented here, agents are equipped with explicit behavioural strategies that depend on information about the other agents. Here, the approach-avoidance conflict has been used to formalise agent rules. Using such a multi-agent model gives a better understanding of the behavioural dynamics of crowd behaviour and of the ways in which it could be influenced. The disadvantages mirror these advantages: multi-agent models are hard to validate empirically, and they often have to rely on anecdotal evidence for their credibility. The reason is that it is difficult to find unequivocal empirical evidence for the very micro-level laws that give the models their richness. It may well be that this 'weakness' of our empirical knowledge is an inherent feature of complex systems (Janssen and De Vries, 1999).

5.3

A great advantage of simulation studies, is that it is easy to do a large number of simulation runs and to compare the aggregated outcomes with empirical data. Especially when the simulation model and the empirical data are matching on some critical macro-level variables (e.g., number of agents, number of parties and symmetrical distribution), it may become possible to test various rules at the micro level by comparing the resulting macro level dynamics against empirical data. Despite the simplicity of our model, we are convinced that our simulation experiments capture some basic factors and processes that occur in large crowds.

5.4

First it was observed that larger groups tend to cluster more than small groups. This may be an effect that can be primarily attributed to the ratio between available space and number of agents. As there are 10.000 cells and only 400 agents there remains however enough open space. Visual inspection of the simulations showed that in all simulations rather large areas were empty, whereas in other areas the agents clearly clustered. Second, it was observed that this clustering develops faster and to a greater extent for asymmetrical groups than for symmetrical groups. Third, we observed that a clustering with other- party members shows a similar pattern to the clustering with own party- members. Especially in the n=400 asymmetrical condition the resulting mixed clusters yield a large number of fights. In the rest of the conditions relative few fights occurred.

5.5

These results are in accordance with what can be observed in the real world. First, people in large crowds tend to cluster instead of spreading themselves evenly over the available space. Moreover, in the real world it can be observed that most crowds assemble and dissemble without large fights. Even when riots occur, it appears that the large majority, typically more than 90% of those present, just watches (Adang, 1998). The simulation results indicate that the risks of fights going out of control is greatest in situations where the crowd is large and the two parties (supporter groups) have a different size. Here the number of hard-core group members seems to play a less important role than the sheer fact of the large numbers and asymmetry. The latter factors seem to promote clustering, which may stimulate a group process towards aggressive behaviour. In real life situations we see that once a confrontation between two unequal parties has started, the smaller party often begins a mass flight as soon as their inferiority in number becomes clear. And even if it is not clear to all, flight seems to have a powerful conformity inducing effect. This effect was not very probable to emerge in our simulation model firstly because it is impossible to escape from the field and secondly as the underlying safety-need and social imitation processes that may propel this behaviour were not formalised. Through visual inspection of the simulations we did however find many instances of clusters of one party moving in a certain direction with a cluster of other party apparently 'chasing' them.

5.6

We are well aware of the simplicity of the approach-avoidance rule that guides the behaviour of our agents. It is however surprising that with so modest a psychological process, the outcomes so much resemble real world phenomena. Just as in out simulation, it often occurs in the real world that people in a group, when confronted with another group, feel more self-confident and are more likely to engage in risky actions. Consequently it might be that this clustering process is a first indicator of a possible escalation. Especially when the proportion of hard-core group members is large, this process may evolve very quickly in time, as our simulation results indicate. These results suggest that measures aimed at preventing fighting at soccer games by separating the groups may cause a clustering that unintended stimulates the aggression motivation. From this perspective it would be more effective to prevent this clustering. An example of the positive effect of cluster-prevention could be found in motor racing and Formula 1 racing, where the fans of different drivers are mixed together, and the relative small stand around the circuit makes it harder to mill over larger distances. This prevents clustering, and indeed fighting during and around such racing events is much less a problem than in many soccer competitions. A thorough study of empirical data is however required validating these preliminary thoughts.

Further Research

6.1

The experiments that we have presented in this paper can be considered as the first basic simulation experiments in the field of aggressive crowd behaviour. On the basis of our simple simulation model many elaborations are possible. One of these possibilities is to enrich the psychological makeup of our agents. The data that our agents gather from their surroundings are quite primitively translated to approach-avoidance of other agents, so it may be worthwhile to elaborate on this process. An example of a more intricate social psychological background for a multi-agent simulation can be found in the consumat approach (Jager, 2000). It would for instance be possible to equip the agents with different needs (e.g., subsistence, protection (safety) and identity (status)). We could try our hand at modelling fatigue in agents, thus motivating them to retreat and go home, modelling of social motives to engage in fights (status), and modelling of (mass)flights when the situation becomes too dangerous. In doing so we could also try to model some well- studied social psychological processes like conformity, social comparison or status differentiation. The possibilities along these lines are almost endless, so we will have to proceed with caution.

6.2

A next issue to improve the simulation model concerns the space in which the agents move. The space in which our simulation took place resembled a square of 100 * 100 metres. In real life situations the space in which riots take place is much less simple. There are streets, stadiums, buildings and various obstacles, none of which appear in our simple square. It would be worthwhile to study how the shape of the space interacts with the behavioural dynamics. Associated with this shape of the space is the entrance and retreat of agents. Whereas the current simulation starts with the agents being randomised over space, it would be of interest to study the effects of starting with an empty space and letting the agents enter. Finally, we intend to spend attention to the type of manifestation that is gong on. In particular we want to distinguish between manifestations with a focus point, i.e. as in a concert, versus manifestations without a clear focus point, such as demonstrations.

6.3

Another real life factor that did not enter our simulation is the fact that quite often one of the parties is much more organised than the other. The more organised party mostly is smaller as well, e.g., a police force. By force of their task, maintenance of public order, it is not feasible for this party to refrain from participation. They have to go on with their job, regardless of happenings and outcomes. While in a normal situation, with two not organised groups, a confrontation between two unequal parties quickly ends with the flight of the smaller group, police groups at best can withdraw tactically. We have as yet no means to put the factor organisation, or task in our simulation, so this again is a possible direction for future research.

6.4

In further experimenting with the simulation model it is important to validate the resulting behavioural dynamics against existing empirical data. Useful empirical data on riots should consist of quantitative descriptions of the way people behave in riot situations (see, e.g., Adang, 1990, 1998). Generally, these descriptions start from the moment when it is clear that 'something is going on', implying a tumult such as the demolition of property or a fight. The stages preceding this moment, which are included in our simulation model, are however very important to understand the development of riots. Therefore we recommend collecting empirical data on these preceding stages. Also it would be worthwhile to collect data on the motives and decision processes of people to engage in a fight or not. Such data may be very valuable in improving the simulation model, both for improving our knowledge on the behavioural dynamics in crowds, as for the development of intervention techniques that avoid the emergence of incidents.

Acknowledgements

The authors would like to thank E. Baas for the programming of the simulation model.

References

ADANG, O., (1990). Geweld en politie-optreden in relsituaties [Violence and police action in riot situations]. Utrecht: University of Utrecht.

ADANG, O., (1998). Hooligans, autonomen, agenten. Alphen aan den Rijn: Samsom.

AXELROD, R. (1997). Advancing the art of simulation in the social sciences. In: R. Conte, R. Hegselmann and P. Terna, (Eds.) Simulating Social Phenomena. Berlin: Springer.

BOUVIER, E., Cohen, E., Najman, L., (1997). 'From crowd simulation to airbag depolyment: particle systems, a new paradigm of simulation.' Journal of Electronic Imaging 6(1), pp. 94-107.

GRANOVETTER, M. (1978) 'Threshold models of collective behavior,' American Journal of Sociology 83 (6): 1420-1443.

HELBING, D. & VICSEK, T. (1999). Optimal Self-Organization. New Journal of Physics 1, 13.1-13.17.

HELBING, D. FARKAS, I. & VICSEK, T. (2000). Simulating dynamical features of escape panic. Nature, 407, 487-490 (2000).

HOGG, M.A. & ABRAMS, D. (1988) Social Identifications: A Social Psychology of intergroup Relations and Group Processes. London: Routledge.

JAGER, W. (2000). Modelling consumer behaviour. Doctoral thesis. Groningen: University of Groningen, Centre for Environmental and Traffic psychology.

JANSSEN, M.A. and DE VRIES, H.J.M. (1999), Global modelling: managing uncertainty, complexity and incomplete information, in: C. van Dijkum, D. de Tombe, E. van Kuijk, (Eds.). Validation of simulation models. Amsterdam: SISWO. pp. 25-69.

LEBON, G. (1952 [1896]) The Crowd. (Translation of: La Psychologie des Foules.) London: Ernest Benn.

MARX, G. & McADAM, D, (1994) Collective behavior and social movements. Englewood Cliffs, Prentice Hall.

McPHAIL, C. (1991) The Myth of the Madding Crowd. New York: Aldine de Gruyter.

MILGRAM, S. & TOCH, H. (1969) 'Collective behavior: Crowds and social movements,' in: Lindzey, G. & E. Aronson (eds.) Handbook of Socal Psychology Volume 4. Reading: Addison-Wesley, 507-610.

MILLER, N.E. (1944) 'Experimental studies of conflict' in: J.McV.Hunt(Ed.) Personality and the behavior disorders. New York: Ronald Press.

MUSSE, S.R., & THALMAN, D., (1997). A Model of Human Crowd Behaviour: Group Inter-relationship and Collision Detection Analysis. Computer Graphics Lab. Swiss Federal Institute of Technology. EPFL, DI- LIG, CH 1015 Lausanne, Switserland. <http://ligwww.epfl.ch/~soraia/Papers/CAS97/CAS97.crowd.doc.html>

REICHER, S. (1987) 'Crowd behaviour as social action,' in: Turner, J.C. (ed.) Rediscovering the Social Group. Oxford, Blackwell, 171-202.

REYNOLDS, C., (1987). 'Flocks, Herds and Schools: A Distributed Behavioral Model.' Proc. SIGGRAPH'87, Computer Graphics, 21, 4, July 1987.

SCHELLING, T.C., (1978). Micromotives and Macrobehaviour. New York: Norton & Company.

TU, X., & TERZOPOLOUS, D., (1994). 'Artificial Fishes: Physiscs, Locomotion, Perception, Behaviour.' Proc. SIGGRAPH'94, Computer Graphics, July 1994.

YIN, J.H., VELASTIN, S., DAVIES, A.C., (1994). Measurement of Crowd Density using Image Processing. VII European Signal Processing Conference, EUSIPCO-94, Edinburgh, UK, Sept.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 2001