Thomas Brenner (2001)

Simulating the Evolution of Localised Industrial Clusters - An Identification of the Basic Mechanisms

Journal of Artificial Societies and Social Simulation vol. 4, no. 3,
<https://www.jasss.org/4/3/4.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary

Received: 13-Oct-00      Accepted: 29-May-01      Published: 30-Jun-01

Abstract

Localised industrial clusters have received much attention in economic research in the last decade. They are seen as one of the reasons for the economic success of certain regions in comparison to others. This paper studies the evolution of such industrial clusters. To this end, a spatial structure of regions is set up and the entry, exit, and growth of firms within these regions is modelled and studied with the help of simulations. Several mechanisms that are often stated to be important in the context of localised industrial clusters are explicitly modelled. The influence of these mechanisms on the geographical concentration of industries is studied.

Keywords:

Industrial clusters, simulations, evolution, spatial agglomeration

Introduction

1.1

Recently regional phenomenon have gained much attention within economics. Especially the question of why certain regions are economically successful while others are not has been frequently discussed. The theoretical discussion of this phenomenon was triggered by various case studies of successful regions, like Silicon Valley, the Third Italy and many more (such case studies can, for example, be found in Rosegrant & Lampe 1992, Saxenian 1994, and Dalum 1995). On the basis of these case studies several authors have attempted to explain the specific reasons for the success of each of these regions. Furthermore, some general concepts have been developed and various mechanisms have been identified that are seen as the causes for the success of those regions. The four main concepts are those of industrial districts, industrial clusters, innovative milieux and regional innovative systems (descriptions can be found in Becattini 1990, Maillat & Lecoq 1992, Pyke & Sengenberger 1992, Scott 1992, Camagni 1995, van Dijk 1995, Markusen 1996, Lawson 1997, Rabellotti 1997; an attempt to identify the most relevant mechanisms within these concepts can be found in Brenner 2000).

1.2

Although the literature on industrial districts and the likes has increased and is still increasing tremendously, most of the literature addresses the reasons for the success of such regional systems and does not deal in general with the question of how these spatial structures come into existence. The question of why such local systems emerge is only addressed in the connection of some specific case studies. In the case of Third Italy historical aspects that led to an entrepreneurial spirit, a trustful atmosphere and helpful politics are suggested to be the determinants (cf. Dei Ottati 1994 and Rabellotti 1997). In the case of Route 128 research funds from the Department of Defence are seen as the initial driving force (cf. Rosegrant & Lampe 1992). While in the case of North Jutland a mixture of a wise creation of new institutes at the Aalborg university, the existence of a firm with experience in the relevant field and the change of the market are regarded to be the crucial factors for the evolution of this district (cf. Dalum 1995). Many other examples could be listed here - all with very specific explanations for specific developments.

1.3

The more general theoretical literature can be divided into two nearly separate strands. One is based on the above-cited case studies and tries to identify general mechanisms that make local systems successful without considering the question of how these mechanisms started. The other is based on the empirical finding that economic activity, on a general and an industrial level, is geographically concentrated (see for example the calculation of gini-coefficients in Krugman 1991a and the calculation of an index of geographic concentration in Ellison & Glaeser 1994). These theoretical approaches have been able to rebuild geographic concentration in simulations (cf. for example Camagni & Diappi 1991 and Jonard & Yildizoglu 1998). However, the aim of these studies was to obtain a final spatial distribution that is similar to the one observed in reality. The dynamics that lead to such a distribution are not discussed in detail in this literature. Thus, a theoretical approach that deals on a general level with the questions of how, where and when localised industrial clusters evolve is missing (a first step into this direction has been taken in Brenner & Weigelt 2001).

1.4

The approach proposed here is based on simulating the spatial dynamics of entries, exits and the growth of firms. Furthermore, most of the mechanisms that have been claimed in the literature to be responsible for the evolution of localised industrial clusters are explicitly included in the model. Altogether seven mechanisms that influence the evolution of localised industrial clusters have been identified (cf. Brenner 2000). The empirical evidence for these mechanisms is various. Some have been shown to exist in many empirical studies, while others have only be supposed to exist on the basis of logical arguments (for a detailed discussion see Brenner 2000 and Brenner & Fornahl 2001). Nevertheless, most of these processes are explicitly modelled here to study their theoretical impact on the evolution of localised industrial clusters.

1.5

To study these local processes a cellular automaton is developed. A grid of 11 (9 regions (in correspondence with the 'Raumordnungsregionen' in Germany) is set up. This means that a two-dimensional space is divided into small quadratic units. This allows dealing with local interactions, both within a unit and between units. Similar approaches are used in the literature on economic agglomeration (cf. Camagni & Diappi 1991, Krugman 1991b, Allen 1997a, Allen 1997b, Schweitzer 1998, and Caniëls & Verspagen 1999) and industrial concentration (cf. Jonard & Yildizoglu 1998). However, the present approach deviates from these approaches with respect to the modelling of firms. Especially the modelling of human capital, technological spillovers, public opinion, regional politics, venture capitalists and spin-offs has not been done, at least not in this combination, in the literature.

1.6

The paper proceeds as follows. In Section 2 the basic model is developed. A sensitivity analysis is conducted in Section 3. In Section 4 the influence of each of the mechanisms is studied in detail separately. Section 5 concludes.

Basic model

2.1

The basic elements of the model are firms. Therefore, the presentation of the model starts with a discussion of the firm-specific variables and their dynamics. Then, the other local elements are defined and their interaction with the firms, their creation and growth, are specified.

2.2

The state of each firm is characterised by several variables which all change endogenously. Furthermore, several parameters are defined that determine the behaviour of firms and their surrounding. These parameters are given exogenously and their influence on the spatial distribution of industrial activity is studied below.

2.3

The variables that define the state of a firm n( ∈ N(t)) at time t(t ∈ {0,1,2,...}) are its labour force L_n( ∈ ℜ₊) and its technology T_n( ∈ ℜ ₊). Furthermore, each firm is assigned to a region q_n( ∈ Q) which cannot be changed during the life of a firm (movement of firms is excluded).

2.4

The firms are assumed to adapt their size to the demand they face. Thus, they do not actively create new markets, but only respond to the changes in the market. This simplifying assumption is made to concentrate the discussion on the aspects that are important for the agglomeration of economic activity and abstract from the complicated process of creativity and fundamental innovation.

2.5

Besides the adaptation to the market situation, three processes that change the state of the firm population are modelled explicitely: The technological improvement of production due to innovations, the change of productivity due to regional changes and the entry and exit of firms. Each of these processes depends on regional circumstances which, in turn, depend on the state of the firm population. These interdependencies are in detail discussed in Brenner (2000). There seven regional mechanisms have been found to play a role. The influence of each of them on the three processes of innovations, firm growth and exit and entry are given in Table 1. Below, first the influence of these seven regional circumstances on the state of each firm are discussed. Then, the dynamics of these circumstances are modelled dependent on the state of the firm population.

Table 1: Influence of several local circumstances on the state of firms
	human capital	spillovers	co-operation	synergies	public opinion	local policies	Venture Capital
innovation	a qualified labour force is more innovative	create innovation and increases diffusion	joint R&D leads to more innovation	-	-	-	-
productivity	qualified labour is more productive	-	joint projects increase productivity	mutually increase productivity	-	support for firms increases their producti-vity	-
start-up	qualified people are more likely to found a firm	-	-	-	a positive expectation increases the number of start-ups	-	start-ups require venture capital

PRODUCTIVITY OF FIRMS

2.6

There is no explicit production function used in this approach, although implicitly a production function is assumed to exist. The productivity of firm n is defined by

(2.1)

where k_q denotes the share of experienced labour force (or human capital) that is available in the region; a_u (0 < a_u < 1), the productivity of inexperienced labour divided by the productivity of experienced labour; C_p,_qn(t) the co-operative activities; M_qn(t) the mutual profits of firms in the region; P_qn(t) the political support (the dynamics of these aspects will be discussed below); and α-βL_n(t) determines whether there are economies of scale. α < 1 is assumed, so that there are never diseconomies of scales for very small sizes of firms. However, if firms increase in size diseconomies might develop (dependent on the value of β). This reflects the fact that the dependence of the production costs on the size of a firm is usually found to be s-shaped.

2.7

The formulation (2.1) implicitly assumes that capital and labour are not substitutes, but complements. The amount of capital always increases and decreases synchronously to the amount of labour used by a firm. Therefore, it is possible to consider only labour explicitly.

INNOVATIONS

2.8

The technology T_n(t) of a firm is driven by innovations and catch-up processes. There is a basis rate of innovations m for each firm which reflects successful research within the firm. It is assumed here that firms are not able to influence this basis rate of innovations. This means that the possibility to vary the amount of R&D-expenditures is neglected. All firms are assumed to spend a certain amount on R&D which is proportional to their size, meaning the number of their employees. In the literature the number of innovations in firms is sometimes found to depend on the size of the firms ( Anselin, Varga & Acs 1997) and sometimes not (see for example Schulenburg & Wagner 1991). Therefore, the internal rate of innovations is assumed here to be the sum of two values: a constant m₀ which is the same for all firms and a value m_L . L_n that is proportional to the number of employees in the firm.

2.9

Besides this internal rate m₀+m_L . L_n innovations are caused by technological spillovers. There is plenty of empirical evidence (cf. e.g. Anselin, Varga & Acs 1997, Audretsch 1998 and Blind & Grupp 1999) for the fact that the research conducted by other firms has an impact on the innovation output of a firm. Furthermore, there is also empirical evidence for the fact, that technological spillovers decrease with the distance between firms (cf. Jaffe, Trajtenberg & Henderson 1993). Finally, it is assumed that firms create the more spillovers, the larger they are. This means that the amount of spillovers increases with the number of employees of the creating firm.

2.10

Furthermore, innovations are also produced by co-operations between firms. It is assumed here that R&D co-operations increase the frequency of innovations. The effect of co-operative R&D in a region is denoted by C_i,_q(t). The respective dynamic is modelled below.

2.11

Finally, a qualified labour force increases the likelihood of innovations. Thus, the human capital in a region influences the amount of innovations by a firm. It is assumed that the human capital available influence the likelihood of all kinds of innovations, namely the internal innovations, the innovations caused by spillovers and those due to joint R&D projects.

2.12

Including all these aspects leads to a probability p_n(t) for firm n to innovate at time t that is given by

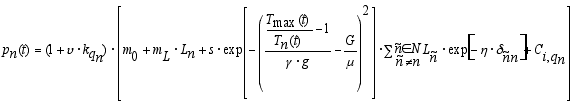
(2.2)

v (>0) is a parameter that determines the increase of the innovativeness of firms due to a higher human capital. s (>0) is a parameter that denotes the strength of the influence that spillovers from other firms have on the innovativeness of a firm. Furthermore, spillovers are assumed to be highest if the technological gap between the technology of the firm and the most advanced technology T_max(t) used by some other firm equals G (> 0). Firms are assumed to profit most from spillovers if they are technologically behind by an amount of G. If the quotient T_max(t)/T_n(t) is less or more than G the effect of spillovers decreases. g_u (>0) determines how much the spillovers decrease for other technological gaps (this aspect of the modelling is taken from Caniëls 1999). In addition, the effect of spillovers decreases with the spatial distance δ_ñn between the firms. η (>0) determines the strength of this effect. The distance between two firms is given by

δñn={[(xqñ - xqn)2 + (yqñ - yqn) 2]}

(2.3)

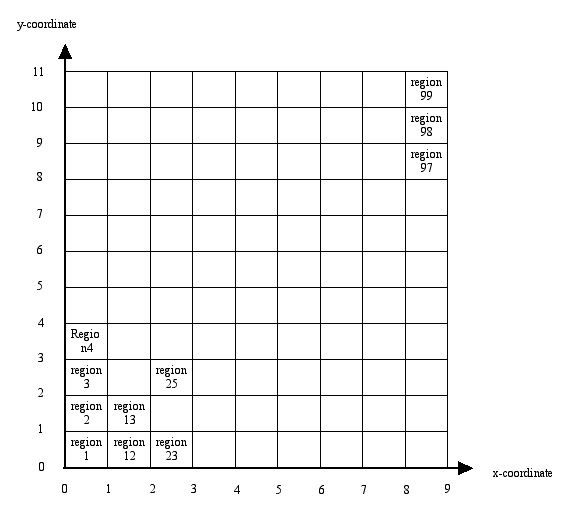
where x_q denotes the x-coordinate of region q and y_q its y-coordinate (coordinates are taken in the middle of a region). In the simulations the regions are assumed to be located as given in Figure 1.

Figure 1. Location of the 99 regions

2.13

Whether a firm n innovates at time t is a random event. The probability of such an event is given by Equation (2.2). All innovations are assumed to be incremental and of the same size.

2.14

Thus, an innovation increases the technology T_n(t) that is used by firm n by a certain fixed amount. This amount is set to γ(T_n(t). Hence, the effect of an innovation at time t is given by

Tn(t+1) = (1+γ) Tn(t)

(2.4)

2.15

Assuming the amount of improvement to be proportional to the current value of T_n(t) causes the impact of an innovation on the productivity of a firm to remain the same over time. Furthermore, the values of T_n(t) are reduced at each time step such that their average equals one. This is done for normation. It hinders the productivity to increase continuously while the demand remains constant.

EXIT AND ENTRY OF FIRMS

2.16

It is assumed that firms exit if their labour force decreases below 1. Two kinds of entries are considered: independent start-ups and spin-offs.

2.17

Start-ups are assumed to appear with a probability in each of the regions that depends on the human capital, the availability of venture capital and the opinion of the population in the region. A basic probability ε_q (>0) for start-ups is assumed that describes the founding process in the initial state. The aspects of human capital k_q(t), venture capital V_q(t) and public opinion towards founding a firm F_q(t) are assumed to have an multiplicative impact on this probability. Mathematically the likelihood of a start-up in region q is given by

(2.5)

where L_q(t) denotes the employment of all firms in region q. The dynamics of K_q(t), V_q(t) and F_q(t) are given below. The technology used by a start-up firm equals the average technology used by all existing firms. The initial technology of the first firm is set to 1. The initial number of employment is randomly determined. It ranges between zero and L_init.

2.18

With a certain probability each firm n creates a spin-off firm ñ. The spin-off firm starts with the technology that firm n currently uses: T_ñ(t) = T_n(t). The initial number of labour used by the spin-off firm is again drawn from a uniform distribution between zero and L_init.

2.19

The probability of a spin-off depends on the number of workers in a firm and again on the human capital, the availability of venture capital and the opinion of the population in the region. The latter variables are assumed to have the same impact on the probability of spin-offs as they have on the probability of start-ups. The more employees a firm has, the more likely one of them founds an own firm. Therefore, the probability of a spin-off from firm n is given by

(2.6)

where φ (>0) is a parameter. Spin-offs are often located near to the firm in which the founder has worked before. In this approach it is assumed that the likelihood for the spin-off firm to be located in a certain region decreases exponentially with the distance from the originating firm. The probability for the spin-off firm ñ to be located in region q is given by

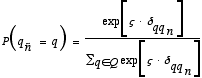
(2.7)

where δ_qqn is defined analogously to δ_nñ (see Equation (2.3)) and ςς(>0) is a parameter that characterises the geographical stickiness of spin-offs.

SIZE OF FIRMS

2.20

The amount of labour L_n(t) that is employed by a firm is determined by the demand for its products. Since capital and labour are assumed to be complements, they always change simultaneously. Firms adapt their labour force to the demand they face (L_n(t) becomes equal to the demand divided by the productivity), if such an adaptation is feasible. It is assumed that labour and capital inputs can be reduced very quickly. In the simulations a maximal reduction by 10% per day is assumed. This assumption does in general not restrict the adaptation towards lower employment, since the market situation changes that fast very seldom. The speed for increasing labour and capital inputs is assumed to be limited to a maximal increase by λ L_n(t) within one time step, meaning one day. This restriction is much more binding, since new firms face very often a demand that is greater than what they can serve.

2.21

The demand function is assumed to be linear. It is given by

(2.8)

where D (>0), b (>0) and ρ (>0) are parameters. For a constant wage and interest rate, the production costs are proportional to the inverse productivity. Assuming that firms use markup-pricing, their price is also proportional to the inverse productivity. Thus, the productivity might be used in the demand function as it is done in Equation (2.8). The last term on the right-hand side of Equation (2.8) represents the impact that other firms have on the demand faced by firm n. Y_ñ(t) denotes the sales of firm ñ at time t. These sales reduce the demand for the products of firm n by ρρ Y_ñ(t) . Thus, ρ denotes the heterogeneity of the goods. For ρ = 0 the goods are completely different and the demand for the product of one firm does not depend on the behaviour of other firms. If ρ = 1, the goods are identical and an increase of sales by one firm does automatically mean a decrease by the same amount of sales of other firms. All firms are assumed to supply the same market, so that the location of firms does not influence the demand for its products.

2.22

If all firms are able to instantly adapt their inputs to the demand, their sales equal the demand for their products. In this case the demand function reads

(2.9)

2.23

Equations (2.9) for all firms constitute a linear equation system for the demands d_n(t). For ρ = 1 this system has no solution if the productivities of the firms differ. Therefore, ρ < 1 is assumed in the following. In this case the equation system (2.9) can be solved. It results in

(2.10)

where N(t) is the number of firms at time t. This equation looks quite similar to the demand function that is usually applied in oligopoly theory (one might redefine the parameters such that the equation looks more convenient). The only real difference is the dependence on the number of firms N(t) which has to be explicitly considered here because this number changes over time endogenously. In the simulations Equation (2.8) is used to calculate the demand for each firm.

HUMAN CAPITAL

2.24

The accumulation of human capital has been found to be crucial for the evolution of industrial clusters. Two kinds of human capital have to be distinguished in this context (cf. Brenner 2000): transferable and non-transferable human capital. In this approach only the non-transferable human capital is explicitly modelled. This kind of human capital is mainly created on the job within firms. Nevertheless, other local actors like universities and research institutes might contribute to the local non-transferable human capital. Thus, it is assumed here that the human capital within a region has a basic value K_init,q and increases proportionally to the number of employees in firms in this region. However, human capital cannot increase unboundedly. It is assumed in this approach that each region contains a certain number of people that might develop the skills and accumulate the non-transferable knowledge that are important in the considered industry. The maximal number of qualified employees is denoted by K_max,q(t). The less people are left in a region that might become qualified, the more slowly does the human capital in a region increase. Therefore, the increase in human capital is proportional to the number of employees and the difference between the maximal human capital and the current one. In addition, a certain share ξ (>0) of the qualified labour force drops out of the labour market at each time, due to retirement, migration and economic change. At the same rate human capital is created by universities and research institutions, so that the human capital in a region cannot decrease below K_init,q. The dynamics of the human capital in region q read:

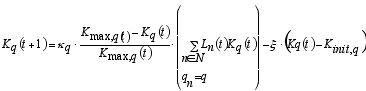
(2.11)

where κ_q (>0) is a parameter that denotes the speed of the accumulation of human capital.

2.25

The maximal number of qualified employees in a region is not constant over time. One specific industry is considered in this approach. Therefore, the amount of people that this industry can attract plays an important role. If the population in the region believes that the industry will develop positively in the future, they will be more willing to invest in education related to this industry. As a consequence, the maximal number of qualified employees that this industry can rely on changes dependent on the expectations of the local population. Therefore,

(2.12)

where I_q(t) is the opinion in the population of region q with respect to the industry. The dynamics of I_q(t) are given below.

CO-OPERATIONS

2.26

Two kinds of local co-operations are considered here: co-operations that increase the likelihood of innovations, mainly R&D co-operations, and co-operations that increase productivity, for example, the joint use of facilities. The consideration is restricted to co-operations within regions. In contrast to spillovers, there is no empirical evidence for a continuous decrease of the likelihood of co-operations with geographical distance. There is evidence for a higher rate of co-operation within regions and within nations. Since the simulations are restricted to one nation, only co-operations within regions seem to matter for this study.

2.27

It is assumed that co-operations lead to a fixed profit, either in form of a certain increase in the likelihood of an innovation denoted by m_C (>0) or in the form of a certain increase of the productivity factor (1+C_p,q(t)) by a_C (>0). However, co-operation is assumed to be a random event. In the simulations in each period it is stochastically determined whether a new co-operation is established. If a new co-operation occurs, the co-operation profits increase according to

(2.13)

(2.14)

2.28

According to Equations (2.13) and (2.14) co-operations that have been established in the past have still an effect on the actual productivity and innovativeness. However, there impact decreases with each time step by a factor of (1-c_a) (where c_a > 0) due to the termination of such co-operations.

2.29

The probability of a co-operation to be established depends on the number of potential co-operation partners in the region and on the attitude of the firms with respect to co-operations. This attitude consists of two parts, a culturally determined basic attitude c_c and an additional value p_c(t) due to experiences in the past. This additional value is assumed to move only upwards, starting from zero and increasing with each successful co-operation. Its maximal value is set to p_max,c and the increase in case of a co-operation at time t is given by

(2.15)

φ (>0) is a parameter that determines the speed of learning about the advantages of co-operation.

SYNERGIES

2.30

It is assumed that firms that are located in the same region mutually profit from each other. Such synergies are assumed to occur automatically and immediately. They may consist of the joint establishment and use of local institutions, joint development of products, joint advertisement and other mutually profitable activities. Most of such activities save costs. Thus, it is assumed that these synergies lead to an increase in productivity as modelled in Equation (2.1)

2.31

Synergies are assumed to occur between all firms. However, proximity increases the effect of synergies. Thus, the amount of mutual profits that a firm n receives is given by

(2.16)

where µ (>0) represents the overall effect of synergies and χ (>0) determines the local stickiness of synergies.

PUBLIC OPINION

2.32

In case studies and analyses of regional developments the public opinion is often found to be relevant. Different mechanisms are identified that cause positive or negative impact on firms due to the attitudes of the local population. According to the concept of innovative milieux, the openness of the local population with respect to technological development is crucial for the innovativeness in a region (see Maillat 1998). In many case studies of Italian districts the specific attitude towards entrepreneurship is highlighted (see e.g. Sengenberger & Pyka 1992).

2.33

This approach considers two kinds of interactions between the population of firms and the public opinion. These are the two mechanisms that seem to be most likely to constitute a self-augmenting process.

2.34

First, the expectations about the future of a region, an industry, and start-ups in this region and industry influence the probability that a person in this region founds an enterprise. The more optimistic people are the more start-ups can be expected to occur. At the same time, the success of start-ups influences the opinion of the population. Successful start-ups increase expectations, while start-ups that have to close down reduce expectations. To model this mechanism, a variable F_q(t) is defined for each region, which starts with a value of zero, increases each time a new firm is founded in the region, and decreases each time a firm has to shut down. It is assumed that the foundation of a new firm increases F_q(t) by f ₊ (>0) and that the shut down of an enterprise decreases F_q(t) by f _- (>0). Furthermore, events that have occurred further in the past have less influence on the actual opinion of the population. Therefore, the value of F_q(t) is reduced at each time according to

(2.17)

where f_m (0<f_m<1) is a parameter that determines the decay of the memory about founding and close down events. The opinion F_q(t) of the local population with respect to founding a firm influences the number of start-ups and spin-offs as modelled in the Equations (2.5) and (2.6).

2.35

Second, the maximal number of experienced labour that the firms of an industry might attract and educate is limited by the number of people and their willingness to work in an industry. Generally, people have to decide quite early in their life about their education. The human capital that is acquired is often specific and it is difficult or at least takes some effort to change between different jobs and industries. Therefore, firms depend on the willingness of people to invest in human capital that is specific to the respective industry or technology. People prefer to invest in human capital that offers them good chances to find a job later on. The local situation is especially important. Thus, the opinion of the local population about the future of different industries matter for the chances of firms to have access to the required human capital. In this approach it is assumed that the local opinion depends on the number of employment in an industry. Industries with a small number of employees are not recognised, while industries with a high number of employees attract people and lead to a positive opinion about the industry. The dynamics of this opinion are given by

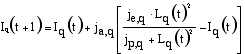
(2.18)

j_a,q, j_e,q and j_p,q are parameters of the region q. For small numbers of employees the dependence has a quadratic form. This reflects the aspect that industries are only recognised if they reach a certain level of employment. For larger numbers the opinion levels off, meaning that it is not able to increase above j_e,q which denotes the maximal effect of this aspect. Furthermore, the public opinion is assumed not to reach this value immediately, but to slowly develop in the direction of this value. The opinion about an industry influences the maximal human capital in a region according to Equation (2.12).

POLICIES

2.36

Local policies can favour a certain industry, so that the firms of this industry become more profitable. There are plenty of ways in which policies can support firms. Without discussing the details of such supports, it is assumed here that political support leads to an increase in productivity. A certain support is in general given to every firm. This basic support is modelled by a value P_q(t) = 1. However, if the employment in a certain industry increases above a certain level L_pol , this industry becomes more influential in local politics. The policy makers can be expected to support the firms of this industry more. This is modelled by an increase of the value of P_q(t) by π. Thus, P_q(t) is given by

(2.19)

where L_pol (>0) is a parameter. P_q(t) influences the productivity of all firms of the industry in region q according to Equation (2.1).

VENTURE CAPITAL

2.37

The local availability of venture capital is crucial for start-ups. This availability might change over time, due to already existing firms in the region. On the one hand, established firms often supply venture capital to start-ups in the same industry. On the other hand, local banks and venture capitalists collect experience in certain industries and are subsequently more willing to lend money to firms in the same industries. Thus, a high number of firms in a certain industry increases the chances for new start-ups in this industry to obtain the required venture capital.

2.38

Here it is assumed that the basic availability of venture capital is V_q(0) = V_init. The value of V_q(t) influences the probabilities of start-ups and spin-offs according to Equations (2.5) and (2.6). It changes according to

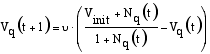
(2.20)

where v (>0) is a parameter and N_q(t) is the number of firms in the considered industry in region q. If the number of firms is very high, the value of V_q(t) converges to one. If, instead, no firm of the considered industry is located in region q, the value of V_q(t) converges to V_init. The speed with which the availability of venture capital adapts to a new situation is given by v.

Analysis of the parameters' impact

3.1

For the sensitivity analysis it is assumed that all parameters are the same for all regions q. Nevertheless, the model has 40 parameters. To understand their influence on the geographic distribution of firms and employment, each of the parameters is varied separately. The analysis of the impact of such a variation is a common method for studying simulations. Usually a basis set of parameters is chosen. Then, each of the parameters is varied separately. However, a parameter might have an impact for certain values of other parameters and might have no impact for others. Therefore, starting with one basic parameter set and varying each parameter separately does not give a comprehensive picture of the influence of the parameters. Therefore, many authors vary several parameter simultaneously. As long as not all parameters are varied simultaneously, however, there is no complete understanding of the parameters impact either. In a case with 40 parameters a simultaneous variation of all of them is not feasible^[1].

3.2

An alternative approach is proposed here. Instead of using a basic set of parameters, a range is defined for each parameter. Within these ranges specific sets are chosen randomly and then one parameter is varied systematically. For each parameter 20 random sets of parameters are chosen. If the variation of the parameter does not lead to any significant change for all 20 sets of parameters, it can be concluded that this parameter has no significant impact^[2]. Otherwise, the results for the different sets of parameters might allow to draw a more comprehensive picture of the possible impacts of the parameters.

3.3

The first step is to define the range for each parameter. Since some of the parameters represent changes per unit of time, the unit of time has to be defined. A time step is set to be one day.

3.4

The maximal initial labour force of start-ups and spin-offs is set to 2 < L_init < 30. Values below 1 are not feasible because L_n(t) < 1 is the condition for the exit of a firm. Empirical studies on German start-ups have shown that a very small proportion has more than 30 employees at the beginning (for a distribution of the size of start-ups see Almus, Engel & Nerlinger 1999). The range for α is set to 1 < α < 1.3. The lower bound is set according to the considerations above and the upper bound is arbitrarily chosen. For β the lower bound is set to zero while the upper bound is arbitrarily set to 0.01. D denotes the maximal number of products that might be sold by a firm. In combination with the productivity it determines the total employment. The initial productivity is 1, but might increase up to around 10 during the simulation. D is chosen such that the total employment ranges between 1000 and 500000, according to the number of employees in different industries in Germany, which implies 10000 < D < 500000. b determines the impact of a firm's price on its sales. This impact might be arbitrarily small, so that the lower bound is set to b > 0. If b is too high, no good can be sold. Therefore, b < D L_init^α is assumed, so that the demand in a monopolistic situation is above zero. ρ describes the heterogeneity of the good produced by different firms. It is assumed that the firms are producing for the same market. Thus, the goods can be assumed to be substitutes. This means ρ can be expected to be rather high. 0.7 < ρ < 1 is assumed. λ determines how much a firm is able to increase its labour force within one time step. In empirical studies in Germany it has been found that most start-up firms grow with a rate of between 0 and 25 % per year (see Almus, Engel & Nerlinger 1999). Here, however, we are interested in the maximal growth rate of firms, meaning the growth rate that occurs if the demand does not limit growth. According to empirical findings (see again Almus, Engel & Nerlinger 1999) the maximal growth rates seem to be at least below 200 % per year. Thus, 0.0001 < λ < 0.003. The lower bound is arbitrarily chosen, implying a maximal growth rate of 4 % per year which surely includes all realistic cases. The probability of independent start-ups is set to 0.00003 < ε_{q <} 0.05 which means that in all 99 regions between 1 and 1800 start-ups occur every year. The upper limit corresponds to half the values found empirically for 2-digit industries in Germany (see Audretsch & Fritsch 1999). This would mean that the upper limit assumes that half of the start-ups occur independent of existing firms. If, instead, all start-ups are spin-offs (with L employees in the industry), ε_q should be set to zero while φ = 10/L should hold according to the values for the 2-digit industries in Germany (see again Audretsch & Fritsch 1999). The maximal number of employees is approximately given by D.

3.5

Thus φ should range between a very small value (set to 0.000003 here) and 10/D. The parameter ς determines the geographic stickiness of spin-offs. It is assumed to range between 0 and 4, where ς = 0 implies no stickiness and ς = 4 implies that a neighbouring region receives only 1 % of the spin-offs that the region itself receives. People obtain industry-specific skills and experiences outside of private enterprises mainly in universities and public research institutes. Considering only those who leave these institutes after some time, their number K_init,q is rather small in a region. It is assumed to range between 0 and 50 here. K_max,q depends very much on the industry and its requirements for specific skills. The range for this parameter is set to 50 < K_{max,q <} 10000. The upper bound is set to the maximal number of people that is on average employed in a region in the 2-digit industries in Germany. The lower bound is set such that K_max,q<K_init,q is always satisfied. The accumulation of human capital is restricted by the speed of acquiring tacit knowledge. The respective parameter is restricted to 0.001 < κ_q < 0.03 which implies that people are not able to acquire the skills that are necessary for a new job in less than 30 days, while the maximal time needed is set to be 3 years. The degeneration of these knowledge or skills is characterised by ξ which ranges between 0.00004 and 0.002. This means that half of the human capital disappears on average in between 1 and 30 years. The former characterises a case where the technology develops such quickly that present knowledge is obsolete in a few years. The latter characterises a situation where knowledge and skills are lost mainly due to retirement. The productivity a_u of inexperienced employees in comparison with experienced employees is only restricted to the theoretically possible range 0 < a_u < 1, because there is no empirical data that allows to draw any conclusion regarding a_u. The increase of the productivity that each innovation leads to is arbitrarily set to 0.000001 < γ < 0.1. This range is chosen to be large enough to include all real cases, since empirical studies on this aspect are not available. The number of innovations that a firm creates per year is intensively studied in the literature. These studies find different dependencies on the size of the firm. Therefore, a constant rate and a rate proportional to the size of the firm are assumed here. For some firms up to 2000 innovations per year have been identified (see Verspagen & Schoenmakers 2000). On average values between 1 and 2 per year and firm are found (see Fritsch, Bröskamp & Schwirten 1996). Therefore, m₀ is set to 0.0003 < m₀ < 0.03 implying a maximal constant number of 10 innovations per year and firm. For the factor m_L a value of around 0.001 is found in the literature (see Blind & Grupp 1999). It varies for different industries between 0.0005 and 0.01 (see Acs & Audretsch 1991). Therefore, 0.0000015 < m_L < 0.00003 is used here. The factor for the additional innovations or catch up processes that are caused by spillovers is restricted in a similar way 0.0000015 < s < 0.00003, so that employees in other firms have a somehow smaller impact on the firm´s innovativeness than employees within the firm. The parameters g and G have to be set arbitrarily due to the lack of empirical evidence. 1 < g < 100 and 0 < G < 10 are chosen here. In correspondence with ς , the range for η is set to 0 < η < 4. Several empirical studies have examined the characteristics of co-operations between firms. Typical numbers of each kind of co-operations range from none to a few. Here it is assumed that between none and 30 co-operations are newly established by each firm. Therefore, 0 < c_{c <} 0.1 is used. The duration of co-operations varies between a few month and several years. Hence, 0.0003 < c_a < 0.02 is chosen for the simulations. The impact of positive experiences with co-operation on the likelihood of co-operation is rather unclear. Huge ranges are chosen for the respective parameters to include reality: 0.00001 < φ < 0.1 and 0.00001 < p_{max,c <} 0.1. Similarly, the impact of co-operation on the innovativeness and productivity of firms is not known. Again huge ranges are chosen: 0.00001 < a_{c <} 0.01 and 0.00001 < m_c < 0.01. The same holds also for the mutual profit that firms obtain from the proximity of other firms. A range of 0.00001 < m_{u <} 0.01 is assumed here. The lower bound is chosen to be quite small. The upper bound is chosen such that with 100 firms located in the same region the increase of productivity does not exceed 100 %. The range for χ is chosen in correspondence to the range of ς : 0 < χ < 4. The ranges for j_a,q, j_e,q and j_p,q are chosen to be very large, because again there is no respective empirical evidence. They are set to 0.000001 < j_{a,q <} 0.1, 0.001 < j_{e,q <} 5 and 50 < j_{p,q <} 10000. The impact of successful start-ups on the readiness of further people to found an enterprise can be expected to be smaller than the impact of failures of start-ups. Therefore, 0 < f _{+ <} 0.01 and 0 < f _{- <} 0.02 are assumed here. The impact of such events can be expected to vanish within some months or a few years. Therefore, the range for f_m is set to 0.001 < f_m < 0.1. Whether local policy makers support certain industries to a larger extend depends on the number of employees in this industry. However, it also depends on the size of the area for which these policy makers are responsible. In small towns 50 or 100 employees might already receive special treatment by policy makers, while in large cities or countries some thousand employees might be necessary to influence policy makers. Therefore, 50 < L_{pol <} 10000. How much local policies might influence the productivity of firms is less clear. 0.00001 < π < 0.1 is assumed here. The venture capital that is available in a region where no firm is located is between zero and one compared to the venture capital that might be maximally available. Therefore, 0.01 < V_init < 1 is used as a range for the initial venture capital availability. If start-ups occur in the region the availability of venture capital increases. The speed of this increase is assumed to range between 0.000001 < v < 0.01, implying that it takes at least three months before the start-ups might provide themselves venture capital for new firms or local banks realise the profitability of supplying start-ups with venture capital. Table 2 summarises the ranges of all parameters.

Table 2: The ranges for all parameters of the model
Parameter	lower bound	upper bound		parameter	lower bound	upper bound
Linit	2	30		g	0	10
α	1	1.3		η	0	4
β	0	0.01		cc	0	0.1
D	10000	500000		φφ	0.00001	0.1
B	0	D		pmax,c	0.00001	0.1
ρ	0.7	1		ca	0.0003	0.02
λ	0.00001	0.003		ac	0.00001	0.01
εq	0.00003	0.05		mc	0.00001	0.01
φ	0.000003	10/D		µ	0.00001	0.01
ς	0	4		χ	0	4
Kinit	0	50		ja,q	0.000001	0.1
Kmax,q	50	10000		je,q	0.001	5
κq	0.001	0.03		jp,q	50	10000
ξ	0.00004	0.002		f +	0	0.01
au	0	1		f -	0	0.02
γγ	0.000001	0.1		fm	0.001	0.1
M0	0.0003	0.03		Lpol	50	10000
ML	0.0000015	0.00003		π	0.00001	0.1
S	0.0000015	0.00003		Vinit	0.01	1
G	1	100		v	0.000001	0.01

3.6

To study the impact of these 40 parameters on the result of simulations, a few variables have to be defined that characterise this result. Five variables are used here. These are the number of firms N after 20 years (7200 simulation steps), the total number of employees after 20 years, the gini-coefficient g for the geographic distribution of employment after 20 years (see Krugman 1991afor a detailed discussion of the gini-coefficient and its calculation), the correlations C₁, C₂ and C₃ between on the one hand the distribution after 5 years (1800 simulation steps), 10 years (3600 simulation steps) and 15 years (5400 simulation steps) and on the other hand the distribution after 20 years (7200 simulation steps). The correlation variables contain some information about the convergence of the processes. Correlation variables of about 1 imply that there are nearly no changes of the firm and employment distribution during the last 15 years of a simulation. This means that the processes have already converged to the final state after 5 years. If, instead, the correlation variables are all approximately zero, no convergence has occurred within the first 15 years of simulation. In addition to these four variables a corrected gini-coefficient is defined. The gini-coefficient that is defined in the literature does not take in the account the total number of firms that are distributed in space. If there is a huge number of firms, the gini-coefficient can take any value between 0 and 0.49495. If, instead, there are only two firms, the gini-coefficient is always greater than 0.48989. Thus, if the number of firms increases due to the variation of a parameter, the value of the gini-coefficient should be expected to decrease. Such a decrease would not imply that the geographic concentration of the industry decreases, but might be the result of the higher number of firms. The corrected gini-coefficient is defined such that it takes into account this fact. For each number of firms the gini-coefficient 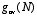can be calculated for a random distribution of N firms of equal size between the 99 regions. is defined as

(3.1)

3.7

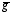Thus, is one if all firms are located in the same region and zero if the firms are randomly distributed over the regions. For a uniform distribution 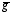becomes negative. These characteristics hold independent of the number of firms.

3.8

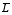For each variation of one parameter the impact on the five variables N, , g, C_i (C₁, C₂ and C₃ generally lead to the same results, so that the average for these three variable is given below), and 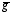is calculated, using regression analysis. This analysis identifies all linear impacts. For each parameter 20 such analyses are conducted for different values of all other parameters. Then, it is calculated how often the studied parameter has a significant positive or significant negative impact on each of the variables. The results are given in the Tables 3 and 4.

Table 3: Influences of the parameters on the variables that characterise the result of the simulation runs. The first value of each entry in the table denotes the number of runs in which significant (significance level: 0,01) positive impact is found. The second value denotes the number of runs in which a significant (significance level: 0,01) negative impact is found.
parameter	runs	N		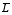g	Ci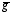
Linit	20	8/3	8/3	5/5	1/4,7	6/4
α	20	2/10	6/6	7/4	3/0,7	5/5
β	20	10/-	2/4	1/7	0,7/2,7	1/5
D	20	8/-	11/-	1/7	3/2	1/-
b	20	-/1	2/1	-/1	0,3/0,3	-/1
ρ	20	-/4	1/6	3/-	-/2,3	2/1
λ	20	2/10	13/1	15/-	3,3/1	10/-
εq	20	18/-	13/-	-/17	2/7,3	1/12
Φ	20	13/-	8/5	2/5	0,7/5,3	7/1
ζ	20	2/5	1/4	12/-	3,7/-	11/-
Kinit,q	20	6/1	3/2	-/7	0,3/3,7	-/7
Kmaxq	20	4/5	5/3	10/1	5,3/0,3	10/-
κq	20	3/5	5/6	8/2	5/1,7	8/2
ξ	20	2/4	3/4	3/2	0,3/1,3	1/2
au	20	4/2	9/2	3/5	2,3/2,7	4/5
γ	20	1/3	-/6	8/-	1,3/2,3	9/-
m0	20	-/2	-/3	-/-	-/1	-/-
mL	20	2/3	-/3	4/-	1,3/-	4/1
s	20	-/1	-/-	1/-	0,7/-	1/-
g	20	-/-	-/-	-/-	0,3/0,3	-/-
G	20	-/1	-/1	1/-	0,3/-	-/-
η	20	-/-	-/-	-/-	-/-	-/-

3.9

This sensitivity analysis helps to identify those parameters that are responsible for certain features. A parameter that has shown no significant influence on a measure for any of the 20 parameter sets can be assumed to really have no impact on this measure. Furthermore, the above analysis allows to identify those parameters whose impact depends on the values of other parameters.

3.10

Tables 3 and 4 reveal that there are quite a number of parameters that do not influence certain variables. Even if there is a significant influence found in one of the 20 runs, it can be assumed that none such influence exists. A statistical test with a significance level of 0.01 should fails in one of 100 cases. This implies that in one of five cases with no influence the entry should be expected to be 1. However, there are also many entries of values above. However, for none of the parameters a significant impact is found in all 20 runs or even 19 runs. This reveals the strong interdependence between the different mechanisms. Every parameter can be made irrelevant by specific values of the other parameters. The impact of some parameters even changes its direction due to changes in the other parameters. Most parameters, however, have either never a significant impact on a certain variable or have a certain impact on this variable which might vanish for certain values of the other parameters. 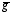For the variable the impact of the parameters is analysed in more detail in the next section.

Table 4: Influences of the parameters on the variables that characterise the results of the simulation runs. The first value of each entry in the table denotes the number of runs in which a significant (significance level: 0.01) positive impact is found. The second value denotes the number of runs in which a significant (significance level: 0.01) negative impact is found.
parameter	runs	N		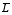g	Ci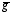
cc	20	-/3	-/7	9/-	2/0,3	8/-
φ	20	-/-	-/-	-/-	-/-	-/1
pmax,c	20	1/-	1/-	-/1	-/0,3	-/-
ca	20	2/-	1/2	-/2	1,3/0,3	-/2
ac	20	3/1	3/3	4/-	0,7/1,3	4/-
mc	20	-/1	-/-	-/-	-/-	1/-
µ	20	1/1	2/1	6/-	1/0,7	6/-
χ	20	2/-	3/2	2/1	1/0,3	2/1
ja,q	20	-/1	-/1	1/-	1/-	-/-
je,q	20	-/1	-/1	1/1	0,3/-	1/1
jp,q	20	-/-	-/-	-/-	0,7/-	-/-
f+	20	-/-	-/-	-/-	-/-	-/-
f-	20	-/-	-/-	-/-	-/0,3	-/1
fm	20	1/-	-/1	-/1	1/-	-/-
Lpol	20	-/-	-/1	1/-	-/-	-/-
π	20	2/1	1/1	3/-	0,3/-	2/-
Vinit	20	14/-	8/-	-/12	1/6	1/11
v	20	10/-	9/-	1/5	-/1,7	5/2

Mechanism that cause geographic concentration

4.1

In the literature seven local mechanisms that might be responsible for the existence of localised industrial clusters have been identified (cf. Brenner 2000). These mechanisms are all included in the above simulation model. Thus, the simulation model offers the possibility to examine whether these mechanisms are in principle able to create geographic concentration. If one of these mechanisms is found to have no influence on the geographic concentration it can be, at least in the form in which it is modelled here, excluded from the list of mechanisms that might be responsible for the existence of localised industrial clusters. The opposite, however, does not hold. A mechanism that has an impact on geographic concentration in the simulations does not necessarily cause the emergence of clusters in reality. The simulations only prove that if such a mechanism is strong enough, it will lead to or support the emergence of clusters. Whether it is strong enough is an empirical question.

4.2

Each of the mechanisms is studied separately below. Before these mechanisms are studied, the parameters that do not belong to one of these mechanisms are discussed.

4.3

The parameters that determine the demand have no or at least no strong impact on geographic concentration. For D, b and ρ only very few significant impacts are found and there is no dominating direction of these impacts. These parameters strongly influence the numbers of firms and employees and might occasionally also have some impact on geographic concentration. However, they seem not to be crucial for the emergence of localised industrial clusters. The initial number of employees of start-ups as well as the amount of economies of scale have in many cases significant impacts on geographic concentration. However, an increase of the respective parameters L_init and α sometimes increases concentration and sometime decreases it. There is no consistent influence. The impacts seem rather to be additional effects of the changes in the size of firms. A somewhat more consistent influence is found for β. The main implication of a high value of β is a decrease in the size of firms. However, this seems also to lead to a decrease in geographic concentration in some cases. The value of λ has a clear positive impact on geographic concentration. This means that if firms are able to grow faster, geographic concentration becomes stronger.

SPIN-OFFS AND START-UPS

4.4

In the literature it is repeatedly claimed that spin-offs and start-ups play an important role in the evolution of industrial clusters. In this approach independent start-ups and spin-offs are distinguished. Table 3 shows that they have different impacts on geographic concentration.

4.5

The frequency of independent start-up ε_q has a clear negative impact on geographic concentration. The more start-ups occur distributed over the entire space, the more likely new centres of economic activity emerge which compete with the already existing ones. This can also be seen in the often negative impact of the frequence of start-ups on the convergence of the process (measured by C_i). A high number of independent start-ups disturbs the spatial distribution of firms and employees. Thus, industries that are characterised by a high number of independent start-ups tend less to be geographically concentrated.

4.6

The opposite holds for spin-offs. Although a high number of spin-offs also disturbs the convergence towards a stable spatial distribution, it increases at the same time geographic concentration. Here the difference between the gini-coefficient and the corrected gini-coefficient becomes obvious. The frequence of spin-offs φ has a mixed and rather negative impact on the gini-coefficient. However, the corrected gini-coefficient reveals that this is due to the increase of the total number of firms which is caused by a high number of spin-offs. Spin-offs have a positive impact on geographic concentration, although this impact depends strongly on the values of the other parameters (it is significant only in around one third of the cases). A positive impact is also, and even more often, found for the parameter ς which describes the local stickiness of spin-offs. This positive impact is found in all cases in which the frequency of spin-offs is at least of about the same size as the frequency of start-ups. Thus, a sufficient number of spin-offs compared with the number of independent start-ups and a sufficient tendency of spin-offs to be founded in the same region as the originating firm creates localised industrial clusters. If the parameters φ and ς are not sufficient large, the mechanism might at least support the emergence of clusters.

ACCUMULATION OF HUMAN CAPITAL

4.7

The accumulation of human capital is identified to be a major force behind the evolution of industrial clusters in nearly all case studies. In this approach five parameters characterise the accumulation of human capital. The parameter K_init,q defines the initial amount of human capital in a region. K_max,q defines the upper limit for the increase of human capital. κ_q characterises the speed of it accumulation. ξ determines the sustainability of human capital. And a_u characterises the increase in productivity that is cause by an increase in human capital. Most of these parameters have a significant impact on geographic concentration. Thus, the simulations confirm the arguments in the literature.

4.8

The speed κ_q of the human capital accumulation has for many parameter sets a positive impact on geographic concentration. The faster human capital is build up in some regions, the better are these regions able to compete with others and hinder them to develop into agglomerations. A similar argument can be applied in the case of K_max,q: the more human capital can be accumulated in a region the less likely is the development of further agglomerations. A fast accumulation of a high amount of human capital in one or a few regions prevents other regions from developing and increases geographic concentration.

4.9

The higher productivity of experienced employees, characterised by a_u, has sometimes a positive and sometimes a negative impact on geographic concentration. A more comprehensive analysis shows that a higher difference in the productivity of experienced and unexperienced labour has two effects. On the one hand, a higher difference favours those regions where already several firms exist and therefore an adequate labour force has been developed. Hence, those regions with a large firm population in the considered industry are likely to grow further. This supports geographic concentration. On the other hand, a high difference in the productivity makes experienced labour crucial for the competitiveness of firms. Thus, the maximal number of experienced employees K_max,q in a region sets a strict limit to the growth of the firm population in a region. If the total number of employees in the industry is higher than this number, some firms have to locate elsewhere. This effect decreases geographic concentration. Therefore, the impact of a_u depends on the relation between D, which determines the total number of employees, and K_max,q.

4.10

The decay of human capital has no clear impact on geographic concentration. Whether experienced employees drop out of the labour market more or less quickly seems not to matter. In contrast, the initial human capital K_init,q matters. It has been argued above that a certain amount of experienced labour might exist in regions due to the movement of employees and the existence of public institutes where people learn the respective skills. This amount of experienced labour is denoted by K_init,q. If it is large in every region, start-ups do well in acquiring the sufficient labour force independent of their location. This lowers geographic concentration. If, instead, firms are the only source of experienced labour, geographic concentration is higher.

INNOVATIONS AND SPILLOVERS

4.11

The basic innovation rate m₀ does not have any impact on geographic concentration. Thus, whether clusters occur in a certain industry does not depend on the frequency of innovations in the industry. This corresponds to the empirical observation that some of the most well-known industrial clusters belong to high-tech industries that are characterised by a high frequency of innovations while others belong to traditional industries with a low rate of innovations. Some influence on geographic concentration is found for m_L. This means that if larger firms are more innovative, the geographic concentration is higher. However, this effect is found only for 20% of the studied parameter sets.

4.12

Much more evident is the influence of the size of innovations on geographic concentration of industries. If each innovation leads to a huge increase (determined by γ) in the productivity of the respective firm, geographic concentration is more likely. Thus, industries where using the most advanced technology leads to a strong competitive advantage are geographically more concentrate than industries where innovations have a small effect on the competitiveness of firms. This holds independent of the frequency of innovations.

4.13

In contrast to the results of other studies (cf. Brenner & Weigelt 2001), spillovers have no impact on the geographic concentration here. For all parameters s, g, G and η that characterise the amount of spillovers no impact is found. This also holds if the value of s is increased significantly. In the study by Brenner and Weigelt spillovers are assumed to have a direct effect on the productivity of a firm. Here they are assumed to increase the probability of innovations. Thus, there are two possible explanations for the fact that spillovers have no impact in this study.

4.14

First, spillover become only relevant when already some agglomeration has occurred. Then, the innovativeness of firms within the agglomeration increases significantly. After some further period of time (after some innovations have occurred) they are able to profit from this higher innovativeness. Hence, the impact of spillovers occurs much later than the impacts of other mechanisms. If the geographic distribution converges to a quite stable distribution, the impact of spillovers might occur too late to influence this distribution. However, in this case we should observe an impact in situations where the geographic distribution does not converge quickly. This has not been observed.

4.15

Second, an increase of the innovativeness of firms due to the proximity might not increase geographic concentration, because this mechanism has not a direct effect. The kinds of spillovers that are modelled in Brenner & Weigelt (2001) are quite similar to what is called here mutual profits. As is discussed below, this mechanism has a significant impact on geographic concentration. Spillovers that increase the number of innovations, however, seem not to have such an effect. This might be connected to the fact that the number of innovations that occur in the industry has also no impact on geographic concentration.

CO-OPERATION

4.16

Local co-operation is often claimed in the literature to be one of the important aspects of industrial districts and clusters. It is argued that co-operation occurs more often within such local systems and is responsible for at least part of their success and therefore also their existence. The simulation results above support such a view. Indeed, local co-operation is able to increase geographic concentration. The parameter c_c, which denotes the basic frequency of co-operation, is found to have a positive impact in 40% of the parameter sets. Thus, if local co-operation takes place very often, the existence of localised industrial clusters is more likely.

4.17

Two kinds of co-operation are considered here: joint R&D projects and the joint use of facilities. The latter seems to be mainly responsible for the impact that co-operations have on geographic concentration. If its strength a_c is increased, geographic concentration increases as well for 20% of the parameter sets. In the case of m_c, which denotes the increase in innovativeness due to joint R&D projects, no clear positive impact is found. Again, like in the case of spillovers, a higher number of innovations due to the proximity of other firms seems not to be able to increase geographic concentration.

4.18

A co-operative attitude that is slowly learnt due to positive experiences with co-operation does also not increase geographic concentration. For the parameters φ and p_max,c no impact is found.

4.19

Hence, local co-operation might cause or support the emergence of localised industrial clusters, if it involves some joint use of facilities or similar co-operations that increase productivity. Such a mechanism, however, is very similar to the one that is modelled as local synergy here. For the additional features of co-operation, like the increase of its frequency due to positive experience and the joint R&D projects, no influence on geographic concentration is found.

SYNERGIES

4.20

The amount of synergies between firms in the same or nearby regions has a positive impact on geographic concentration. However, again this impact is very much influenced by the values of other parameters. A positive impact of the parameter µ is only found for 30% of the parameter sets. Nevertheless, the more firms profit from the proximity of other firms of the same industry the more they cluster.

4.21

The parameter χ has a less clear impact. This implies that local synergies support geographic concentration, independent of the degree of proximity that is necessary for such synergies.

PUBLIC OPINION

4.22

Two mechanisms that involve the public opinion in a region are considered in the simulations. First, people are assumed to invest more likely in skills related to industries that are dominant in the region. As a consequence, the respective firms find it more easy to employ skilled people. Second, it is assumed that the public opinion with respect to founding a firm depends on the experience of already existing enterprises in the region. An optimistic attitude towards founding a firm increases the number of start-ups and spin-offs in the region.

4.23

The first mechanism is characterised by the parameters j_a,q, j_e,q and j_p,q. These three parameters have no significant effect on the geographic concentration of industries. This means that a mechanism based on a higher willingness of people to invest in skills that are related to an industry that employs many people in the region does not increase the geographic concentration of this industry. This holds although the number of potentially skilled people in the region might increase ten fold and this number has been found to have a positive impact on geographic concentration.

4.24

Similarly, the simulations show no significant impact of the parameters f₊, f_- and f_m on the geographic concentration. This contradicts the intuition that a dependence of the entrepreneurial attitude on the success of other local entrepreneurs supports the emergence of clusters. Larger ranges for the parameters than the ones given in Table 2 do not change this result.

4.25

Hence, both mechanisms that are based on changes in public opinion and that are tested here do not lead to a clustering of the industrial activity. This, of course, does not exclude the existence of other mechanisms based on public opinion that might increase geographic concentration. However, so far none such mechanism has been identified.

LOCAL POLICY

4.26

For the parameter L_pol no impact on geographic concentration is found, while π has at least in a few cases a significant positive impact on geographic concentration. However, such an impact is only found for 10% of the parameter sets. This implies that dependent on the other parameters a local policy that supports those industries that are dominant in the region might cause or support clustering. However, in most cases such a local policy has no impact on geographic concentration. The influence of the mechanism of an increasingly supportive local policy once some industrial activity has clustered in a region is rather weak.

LOCAL PROVISION OF VENTURE CAPITAL

4.27

If the local availability of venture capital increases significantly with an increasing number of firms in the region, as a low value of V_init suggests, localised clusters become more likely. Thus, a mechanism that is based on a positive impact of local firms on the availability of venture capital for further enterprises might cause geographical concentration. Again there are no empirical studies that confirm or contradict such a mechanism. This approach is only able to state that if such a mechanism occurs in reality, it is able to cause or support the emergence of localised industrial clusters. Whether this higher availability of local venture capital occurs immediately or takes some time to be established has no consistent impact on geographical concentration. In some cases it is found to have a positive impact, in some cases it has a negative impact and in most cases it has no significant impact.

Conclusion

5.1

This paper presents a proposal for the modelling of the evolution of localised industrial clusters. In the literature several mechanisms are identified which are claimed to be involved when industrial clusters evolve. For some of these mechanisms the existence has been proved empirically. However, this does not necessarily imply that they are responsible for the evolution of industrial clusters. Other mechanisms are only postulated.

5.2

With the help of simulations all these mechanisms are studied here. Through this it can be tested whether, given that the mechanisms work in reality, they might cause clustering. It has been found that the assumed mechanisms involving public opinion and spillovers do not add to the emergence of localised industrial clusters. However, several aspects that might influence the existence of clusters are identified. Industries which are characterised by a high possible growth rate of start-ups, by radical innovations, by a strong importance of experienced employees with firms as the only source of these, by a large number of spin-offs, that are started near their incubator institution, by the provision of venture capital by existing firms, or by local synergies of firms in the same industry, are more likely to cluster.

5.3

Furthermore, a new kind of sensitivity analysis has be proposed that seems to be very helpful in this context. The high number of parameters made such a new approach necessary. With the increasing possibility to treat complex systems with the help of simulation the use of new tools to analyse the results of these simulations becomes crucial. Computational economics could profit from more discussions on this subject.

5.4

Finally, this approach offers a starting point for further research. First, it allows to analyse the impact of different policy measures. The parameters can be set according to policy activities in certain regions and their implications can be studied. Second, quite some of the parameters used in this approach can be empirical estimated for certain industries. Thus, certain industries can be simulated. The results can be compared with the distribution of employment in the 97 ´Raumordnungsregionen´ in Germany. On the basis of this comparison it should be possible to figure out, which mechanisms dominate in which industries.

5.5

In addition, it is possible to adapt the simulation model even more to reality by using the real positions of the 97 ´Raumordnungsregionen´ and including regional circumstances in the model, like the location of universities and research institutions. This should allow for studying the impact of these circumstances for the geographic distribution of employment.

Acknowledgements

I want to thank Ulrich Witt, Dirk Fornahl, Guido Bünstorf, Rainer Voßkamp, Paolo Saviotti, Max Keilbach, Niels Weigelt and the participants of the meeting of the Ausschuss für Evolutionsökonomik for their helpful comments and discussions and the German federal ministry for education and research for financial support. The usual disclaimer applies.

Notes

¹ Even if the analysis is restricted to two values for each parameter, more than $1 000 000 000 000$ runs are necessary with each of them taking approximately 5 minutes.

² Of course, this statement in principle only holds if an infinite number of random sets is chosen. However, the more sets of parameters are chosen, the more reliable is the obtained result.

References

ACS, Z.J. & AUDRETSCH, D.B. (1991). Innovation and Small Firms. Cambridge: MIT Press.

ALLEN, P. M. (1997A). Cities and Regions as Evolutionary, Complex Systems. Geographical Systems 4, 103-130.

ALLEN, P. M. (1997B). Cities and Regions as Self-Organizing Systems. Models of Complexity. Amsterdam: Gordon and Breach.

ALMUS, M., ENGEL, D. & NERLINGER, E. A. (1999). Determinanten des Beschäftigungswachstums junger Unternehmen in den alten und neuen Bundesländern: Bestehen Unterschiede hinsichtlich der Technologieorientierung?. Zeitschrift für Wirtschafts- und Sozialwissenschaften 119, 561-592.

ANSELIN, L., VARGA, A. & ACS, Z. (1997). Local Geographic Spillovers between University Research and High Technology Innovations. Journal of Urban Economics 42, 422-448.

AUDRETSCH, D. B. (1998). Agglomeration and the Location of Innovative Activity. Oxford Review of Economic Policy 14, 18-29.

AUDRETSCH, D. B. & FRITSCH, M. (1999). The Industry Component of Regional New Firm Formation Processes. Review of Industrial Organization 15, 239-252.

BECATTINI, G. (1990). The Marshallian Industrial District as a Socio-economic Notion. In: (Pyke, F., Becattini, G. and Sengenberger, W., Eds.) Industrial Districts and Inter-firm Co-operation in Italy, pp. 37-51. Geneva: International Institute for Labour Studies.

BLIND, K. & GRUPP, H. (1999). Interdependencies between the Science and Technology Infrastructure and Innovation Activities in German Regions: Empirical Findings and Policy Consequences. Research Policy 28, 451-468.

BRENNER, T. (2000). The Evolution of Localised Industrial Clusters: Identifying the Processes of Self-organisation. Papers on Economics & Evolution #0011, Max-Planck-Institute Jena.

Brenner, T. & Fornahl, D. (2001). Theoretische Erkenntnisse zur Entstehung und Erzeugung `innovativer Regionen´. mimeo, Max-Planck-Institute Jena.

Brenner, T. & Weigelt, N. (2001). The Evolution of Industrial Clusters - Simulating Spatial Dynamics. Advances in Complex Systems 3, (forthcomming). CAMAGNI, R. P. (1995). The Concept of Innovative Milieu and Its Relevance for Public Policies in European Lagging Regions. Papers in Regional Science 74, 317-340.

CAMAGNI, R. P. & DIAPPI, L. (1991). A Supply-oriented Urban Dynamics Model with Innovation and Synergy Effects. In: (Boyce, D. E., Nijkamp, P. and Shefer, D. ,Eds.) Regional Science, pp. 339-357. Berlin: Springer-Verlag.

CANIËLS, M. (1999). Regional Growth Differentials. Maastricht: Dissertation.

CANIËLS, M. C. J. AND VERSPAGEN, B. (1999). Spatial Distance in a Technology Gap Model. Working Paper 99.10, Eindhoven Centre for Innovation Studies.

DALUM, B. (1995). Local and Global Linkages: The Radiocommunications Cluster in Northern Denmark. mimeo, Aalborg University.

DEI OTTATI, G. (1994). Cooperation and Competition in the Industrial District as an Organisation Model. European Planning Studies 2, 463-483.

ELLISON, G. AND GLAESER, E. L. (1994). Geographic Concentration in U.S. Manufacturing Industies: A Dartboard Approach. Working Paper No. 4840, National Bureau of Economic Research.

FRITSCH, M., BRÖSKAMP, A. & SCHWIRTEN, C. (1996). Innovationen in der sächsischen Industrie - Erste empirische Ergebnisse. Freiberg Working Papers 96/13, Technical University Bergakademie Freiberg.

JAFFE, A.B., TRAJTENBERG, M. AND HENDERSON, R. (1993). Geographic Localization of Knowledge Spillovers as Evidenced by Patent Citations. Quarterly Journal of Economics 79, 577-598.

JONARD, N. AND YILDIZOGLU, M. (1998). Technological Diversity in an Evolutionary Industry Model with Localized Learning and Network Externalities. Structural Change and Economic Dynamics 9, 35-53.

KRUGMAN, P. (1991A). Geography and Trade. Cambridge: MIT Press.

KRUGMAN, P. (1991B). Increasing Returns and Economic Geography. Journal of Political Economy 99, 483-499.

LAWSON, C (1997). Territorial Clustering and High-Technology Innovation: From Industrial Districts to Innovative Milieux. Working Paper No. 54, ESRC Centre for Business Research, University of Cambridge

MAILLAT, D. (1998). From the Industrial District to the Innovative Milieu: Contribution to an Analysis of Territorialised Productive Organisations. Recherches Economiques de Louvain 64, 111-129.

MAILLAT, D. AND LECOQ, B. (1992). New Technologies and Transformation of Regional Structures in Europe: The Role of the Milieu. Entrepreneurship & Regional Development 4, 1-20.

MARKUSEN, A. (1996). Sticky Places in Slippery Space: A Typology of Industrial Districts. Economic Geography 72, 293-313.

PYKE, F. AND SENGENBERGER, W., EDS (1992). Industrial Districts and Local Economic Regeneration. Geneva: International Institute for Labour Studies.

RABELLOTTI, R. (1997). External Economies and Cooperation in Industrial Districts. Houndmills: Macmillan Press Ltd.

ROSEGRANT, S. AND LAMPE, D. R. (1992). Route 128. Basic Books.

SAXENIAN, A.-L. (1994). Regional Advantage. Cambridge: Harvard University Press.

SCHULENBURG, J.-M. & WAGNER, J. (1991). Advertising, Innovation and Market Structure: A Comparison of the United States of America and the Federal Republic of Germany. In: (Acs, Z.J. and Audretsch, D.B., Eds.) Innovation and Technological Change, pp. 160-182. New York: Harvester Wheatsheaf.

SCHWEITZER, F. (1998). Modelling Migration and Economic Agglomeration with Active Brownian Particles. adv. complex systems 1, 11-37.

SCOTT, A. J. (1992). The Role of Large Producers in Industrial Districts: A Case Study of High Technology Systems Houses in Southern California. Regional Studies 26, 265-275.

SENGENBERGER, W. & PYKE, F. (1992). Industrial Districts and Local Economic Regeneration: Research and Policy Issues. In: (Pyke, F. and Sengenberger, W., Eds.) Industrial Districts and Local Economic Regeneration. Geneva: International Institute for Labour Studies.

VAN DIJK, M. P. (1995). Flexible Specialisation, The New Competition and Industrial Districts. Small Business Economics 7, 15-27.

VERSPAGEN, B. & SCHOENMAKERS, W. (2000). The Spatial Dimension of Knowledge Spillovers in Europe: Evidence from Firm Patenting Data. mimeo, ECIS and MERIT.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 2001