In this paper, we present several experiments of belief propagation in multi-agent communities. Each agent in the simulation has an initial random vocabulary (4 words) corresponding to each possible movement (north, south, east and west). Agents move and communicate the associated word to the surrounding agents, which can be convinced by the 'speaking agent', and change their corresponding word by 'imitation'. Vocabulary uniformity is achieved, but strong interactions and competition can occur between dominant words. Several moving and trusting strategies as well as agent roles are analyzed.

Keywords:

Multi-Agent systems, Agent-Based simulation, Self-Organization, Language

Introduction

1.1

Computer modelling of large communities (Resnick 1999) is an active area of research. Several objectives can be pursued with this kind of simulation:

• Resolution and optimization of mathematical problems (Dorigo and Maniezzo, 1996).
• Study of emergent global behaviour and social interactions (Edmonds 1998), (Dautenhahn 1997). In this paper, we will focus on this kind of experiment.
• Study of population tendencies and evolution (Ophir, 1998).

Obviously, validation of simulations of types two and three is difficult, sometimes impossible. Care must be taken when making generalization and analogies from simulation results. Nevertheless, by means of computer simulation, we can obtain data that would be impossible to obtain by other means, or at much lower cost.

1.2

Social interactions can be simulated in several ways:

• By means of robotic artefacts (Dautenhahn 1999).
• By means of software artefacts. In this case, several techniques and formalisms have been applied successfully to community simulations, among others:
• Software agents, in which individuals are treated as separate entities able to exhibit autonomous behaviour in a common micro-world. Some kind of intelligence can be assigned to each agent (Wooldridge et al 1995).
• Genetic programming, where individuals are usually much simpler than in the previous case, but the emphasis is put on evolution rather than on social interactions.
• Cellular automata, in which the micro-world is represented as a regular n-dimensional grid, where the state of each cell at a given time step depends on simple rules involving the cell neighbours (Hegselmann and Flache, 1998).

1.3

Our approach is similar to software agents, but agent complexity is reduced to a minimum: their behaviour is governed by simple rules, limited memory and limited world perception. To build the models, we use our own object oriented simulation language: OOCSMP (Alfonseca et al., 1999), which is specially suitable when simulated systems are made of similar interacting entities that can be modelled as objects. Our compiler for this language generates Java applets and HTML pages from the simulation models. We have generated an electronic version of this paper (with interactive on-line simulation instead of static images) that can be accessed at: http://www.ii.uam.es/~jlara/investigacion/ecomm/otros/JASSS.html. Other courses and interactive articles generated with these tools can be accessed from: http://www.ii.uam.es/~jlara/investigacion.

1.4

In this paper, we describe several experiments related to the propagation of information and beliefs in systems of agents that try to achieve a common vocabulary, associated with the spatial movements of the agents. Our goal is the study of the dynamics of eventual convergence on a common vocabulary. In some of these situations, the influence of agent roles (sceptic, credulous) are examined. Different moving strategies are tested to reduce the time needed to reach convergence.

1.5

Similar approaches have been proposed, for example, in Oliphant (1996), where evolution is used to develop a common language, while we put stress on the spatial organization of the agents. Luc Steels (1995;1996;1998) proposes naming games, where agents use extra-linguistic elements to point to the object they want to talk to; the agents also record information about all the words they have heard. In our experiments, however, the object of communication is the movement of the agents; our agents are also much simpler and only need to know the words they prefer to use and the degree of their confidence in those words. Other research that goes beyond the scope of the present work can be found in Kirby (1998)and Hurford (1999). Interaction games are reviewed in Nehaniv (2000). Our work has also some common points with memetics (Dawkins, 1976), in which the replicating units are the ideas (Hales, 1998). However, our agents do not transmit ideas or guides for agents' behaviour, at least in a direct form. Nor do we consider evolution or reproduction. What our agents transmit are 'words' that name each of their possible movements.

1.6

The paper is organized as follows: section 2 presents the world of the 'talking bugs' and the basic experiments. In section 3, we describe some other experiments that add non-determinism to the way agents trust each other. In section 4, we present several agent strategies for belief transmission. In section 5, experiments are carried out with roles. Finally, in section 6, we present the conclusions and consider future work.

The world of the 'talking bugs'

2.1

Our micro-world is a 20 × 20 mesh, with the north mesh border connected to the south border and the east to the west in the form of a plane torus. The mesh defines the number of different agent positions, in this case 400. The mesh is inhabited by agents. Each position can be occupied by zero or more agents. Agents have a word to designate their movements to the north, east, west and south. In our experiments, each agent will start with a random word for each direction, and there are 1000 different words. In the simulation, a word is represented by an integer number. At each time step, every agent will first move randomly, then communicates the word associated with its latest movement to the agents it encounters. If their words are different, each colliding agent has to decide to believe in the other agent (and change its own word) or to maintain its previous belief.

2.2

For this basic experiment, each agent has a 'belief indicator', that measures the degree of confidence the agent has for each word in its vocabulary. This indicator grows (is reinforced) when the agent finds another agent that uses the same word. If two colliding agents use different words, the agent with less confidence changes its word. When both confidence levels are the same, the others' word is adopted.

2.3

In summary, the simulation loop consists of three main steps:

1. Each agent chooses a movement (in this first case, randomly).
2. Each agent moves to a new location.
3. The agents sharing the same location 'talk to each other'. For the basic experiment, the agent with the strongest belief keeps its word, the others change their word and their associated belief indicator to the 'winning' word. Each agent in the same location takes turns to communicate to the others the word associated with its last movement. This experiment is a kind of 'imitation' game: one agent shows the others how it names one movement, the others imitate it if they are convinced, i.e. if they have lower or equal belief indicators.

2.4

The following is a pseudo-code description of our model. We start by defining an agent:
 

[1] An Agent is composed of
[2]   x,y      : [1..20].
[3]   movement : [1..4].
[4]   words    : Array [1..4] of [1..1000].
[5]   beliefs  : Array [1..4] of Integer.
[6]   method choose-movement.
[7]   begin-method
[8]     set movement as a random number between 1 and 4
[9]   end-method
[10]  method move
[11]  begin-method
[12]    update x and y according to movement.
[13]  end-method
[14]  method listen-to ( Agent speaker )
[15]  begin-method
[16]   if ( words[speaker.movement] == speaker.words[speaker.movement] ) then beliefs[speaker.movement]+= 1.
[17]   else if (beliefs[speaker.movement] <= speaker.beliefs[speaker.movement]) then
[18]   begin-if
[19]     words[speaker.movement] := speaker.words[speaker.movement]
[20]     beliefs[speaker.movement] := speaker.beliefs[speaker.movement]
[21]   end-if
[22]  end-method
[23] End of Agent definition

Listing 1: Pseudo-code to define an agent.

Lines 2 to 5 define the agent state:

• x and y are the coordinates of the current agent position in the mesh.
• movement is the direction of the last movement of the agent (in the implementation, a number from 1 to 4)
• words is an array that stores the word associated with each possible movement. Initially, these words are chosen at random between 1 and 1000.
• beliefs is another array that holds the degree of belief associated with each word. Initially, all beliefs are initialized to 1.

Line 6 to 22 define the agent actions:

• choose-movement: is a method that chooses a movement and stores it in state variable movement.
• move: is a method that updates the agent position according to movement.
• listen-to: Is a method called by another agent that takes the role of the speaker (see next listing). It tests if the word used by the speaker and the listener are the same. In that case (line 16), the listener increases its confidence in the word. If the words are different and the speaker has more confidence in the word (line 17), the listener changes its word and its belief indicator to those of the speaker (lines 18 and 19).

For brevity, in the pseudo-code, the agents have direct access to each other's states. In the implementation, this is done via method invocation. This means that, to communicate, the speaker tells the listener the word associated with its movement and its belief indicator.

2.5

The following is the pseudo-code of the main simulation loop.

[1]  While (not converged)
[2]    For each agent [a]: a.choose-movement()
[3]    For each agent [a]: a.move()
[4]    For each position [p] in the mesh:
[5]    begin-for
[6]      For each agent [a] in p:
[7]      begin-for
[8]        For each agent [b] in p:
[9]        begin-for
[10]         if (a <> b) then b.listen-to (a)
[11]       End-For
[12]     End-For
[13]   End-For
[14] End-While

Listing 2: Pseudo-code of the main simulation loop.

The termination condition for the simulation (line 1) is that all agents share the same word for every movement direction. In each loop, the agents first choose a direction (line 2). In the basic situation, the choice is made at random. Next every agent moves according to its selection (line 3). After that, if there is more than one agent in some position of the mesh, the interaction between agents begins: each agent takes successively the role of the speaker, and communicates with the others in the same position, by calling their listen-to method.

2.6

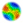
We have done experiments with 400, 600 and 1000 agents. In all cases, the simulation ends with a common vocabulary for all movements. For example, in 40 simulations with 1000 agents, we obtained vocabulary agreement at time 550 on average, with a standard deviation of 260. Notice that there is not an a priori 'better word'; agents don't have any global information about the situation and only local interactions are allowed. Figure 1 shows a snapshot of one of the simulations. The upper left panel shows the mean deviation of the four words in the agent community. When the deviation reaches zero for a word, general consensus has been reached to designate the associated movement. The upper right panel shows a listing with the means of the words. When the deviations are all zero, this panel shows the word that the community has chosen to designate each movement. The lower left panel shows the means of the belief indicators in the community for each word. In this basic situation, this quantity always grows. The lower right panel shows a map of the agent positions. The colors represents the words chosen for the 'north' movement. This panel is specially interesting, because it is possible to observe the dynamics of word changes during the simulation.

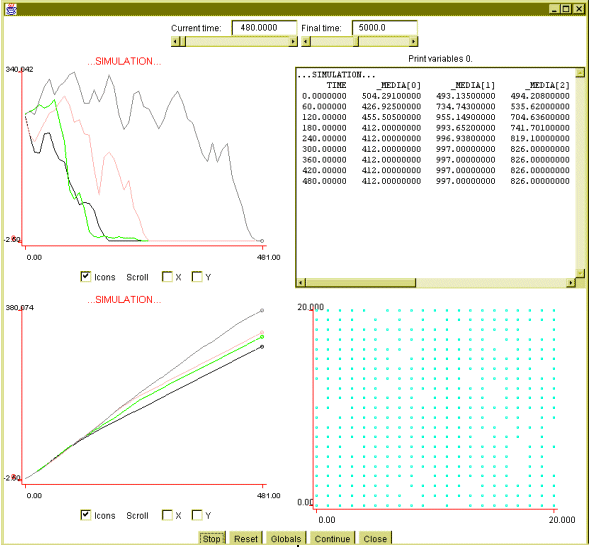
Figure 1: 1000 agents simulation, basic experiment, vocabulary achieved: 412, 997, 826, 194

2.7

In our results, the time to reach a uniform vocabulary does not depend on the number of agents in the simulation within the range from 400 to 1000 agents. It can be observed that the belief indicators increase faster for the word that takes longest to reach a general agreement. It is always like this in this basic experiment. Sometimes acquisition of uniformity for a particular word takes a long time, and the mean deviation panel shows a straight line parallel to the X-axis. The cause of this delay is that the agents split into two sets, each group believing in their own word to a similar degree. Belief indicators grow much faster in these situations.

2.8

To study this phenomenon, we have designed another experiment: in this case, two populations of agents are formed initially, each with its own fixed vocabulary (100, 200, 300 and 400 for one population, 500, 600, 700 and 800 for the other). Furthermore, initial beliefs are set to 300 for the first two words and to 1 for the third and fourth word. This experiment tries to discover whether the delay in acquiring uniformity depends on how strong beliefs are, and on the number of words.

2.9

We have found that the delay is not related to how strong the beliefs are, but it is related to the number of different words in the population, and to how similar the belief indicators are among the two populations. When only two words exist for each movement, delays occur often. The behaviour of the system also depends on whether both populations are mixed in space, or initially separated. In the first case, uniformity may be reached very quickly. This is because in a draw case a dominant word remains, and also due to the deterministic way of changing the word. But even in the case of initially mixed populations, there are cases when uniformity takes a long time to be reached.

2.10

In figure 2, we show an experiment with two different initial words for each movement and separate populations of 500 agents each, located at both sides of an imaginary line dividing the micro-world into two equal halves.

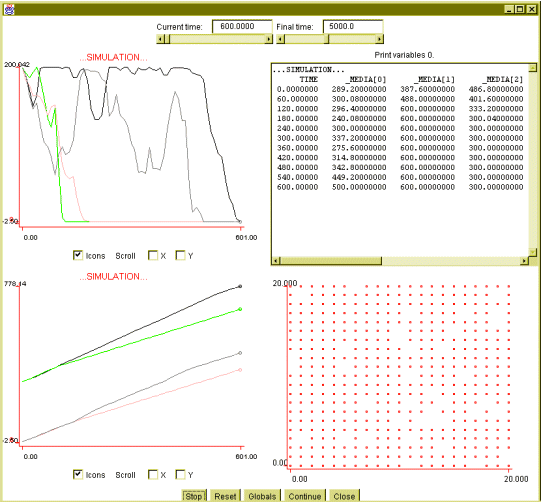
Figure 2: 1000 agents simulation, two initial populations, vocabulary achieved: 500, 600, 300, 400.

It can be observed from Figure 2 that uniformity is soon reached for two of the directions of movement. One of the words had an initial belief of 300, the other started with 1. The other two words take much longer to reach uniformity. The case of the first of these words is interesting (column MEDIA[0] in the listing panel, black color in the graphics): the two possible words are 100 and 500, so the mean oscillates around 300, with a deviation of 200, until one of the words 'wins'. The beliefs associated with this word increase faster than for the other words.

2.11

Figure 3 shows a similar experiment, but the panels have been changed to show the belief indicators for the word associated with the 'north' direction (left panel) and the population of each set of agents (right panel).

Figure 3: 1000 agents simulation, two initial populations. Belief indicators (left) and number of individuals (right).

Obviously, the population curves (right panel) are symmetric with respect to a line parallel to the x-axis and with a height of 500. It can also be noted that the derivative of the population always has the same sign as the derivative of the belief indicators. In fact, the belief indicator curves and the population curves (for the same population) are very similar.

2.12

Simulations with three different populations have also been carried out. Situations when one word disappears and two words interact, as in the previous simulation, are common.

Trusting strategies

3.1

In this set of experiments, we have added non-deterministic behaviour ('noise') to the way agents trust each other. When several agents share the same position, each agent takes turns to 'talk' to the rest, as before, but an agent is 'convinced' in a non-deterministic way. When an agent is listening to the 'talking' agent, it has a probability of being convinced, computed as otherBelief/(ownBelief+otherBelief), where ownBelief is the belief of the agent in its own word, and otherBelief is the belief of the other agent in the word describing the same movement. The listen-to method in Listing 1 has been modified in the following way:

[14]  method listen-to ( Agent speaker )
[15]  begin-method
[16]   if ( words[speaker.movement] == speaker.words[speaker.movement] ) then beliefs[speaker.movement]+= 1.
[17]   else if (random()>beliefs[speaker.movement]/(beliefs[speaker.movement]+speaker.beliefs[speaker.movement])) then
[18]   begin-if
[19]     words[speaker.movement] := speaker.words[speaker.movement]
[20]     beliefs[speaker.movement] := speaker.beliefs[speaker.movement]
[21]   end-if
[22]  end-method

Listing 3:Changes in listing 1, non-deterministic behaviour.

3.2

In these experiments, uniformity takes longer to appear, and simulations with long-time uniformity also occur. In 40 experiments with 1000 agents, we obtained vocabulary agreement at time 590 on average, with a standard deviation of 180. Figure 4 shows a simulation with 600 agents, where two populations of agents with two different words coexist (MEDIA[0], black color in the graph). In the lower right graphic, the populations can be observed, with colors green and blue representing the two different words.

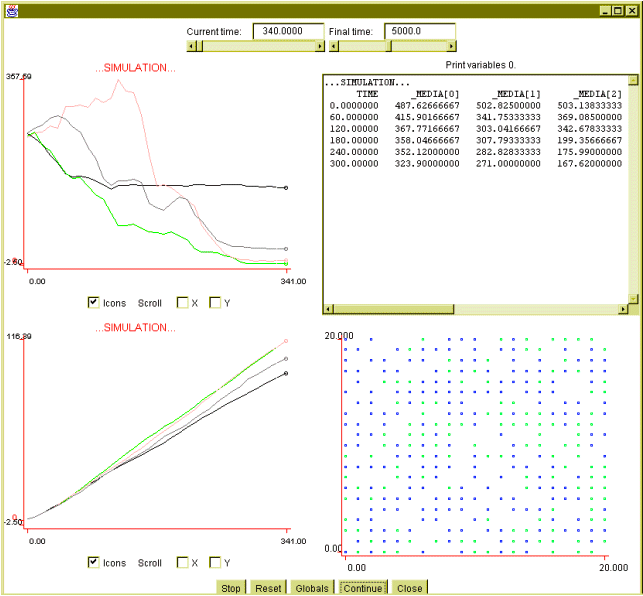
Figure 4: Two interacting populations. Non-deterministic trusting. Two populations of agents with different 'North' word.

It can be seen that, with non-determinism, words that take longer to reach uniformity are associated with lower beliefs, in contrast to the behaviour of communities of deterministic agents.

3.3

This model is autocatalitic: belief indicators always grow. To avoid this, and to make the model more realistic, we have modified it to make belief indicators decrease when an agent shares the same position with another agent that has a different word associated with the same movement, and the second agent is not convinced by the first. Some acceleration in the time for uniformity is obtained (in 40 experiments with 1000 agents, we obtained vocabulary agreement at time 550 on average, with a standard deviation of 160). In this case, lonely agents with words different from their neighbors are quickly 'convinced' by them. Even in this case, the curves for belief indicators exhibit increasing belief. The modifications to the pseudo-code in listing 1 are:
 

[14]  method listen-to ( Agent speaker )
[15]  begin-method
[16]   if ( words[speaker.movement] == speaker.words[speaker.movement] ) then beliefs[speaker.movement]+= 1.
[17]   else if (random()>beliefs[speaker.movement]/(beliefs[speaker.movement]+speaker.beliefs[speaker.movement])) then
[18]   begin-if
[19]     words[speaker.movement] := speaker.words[speaker.movement]
[20]     beliefs[speaker.movement] := speaker.beliefs[speaker.movement]
[21]   end-if
[22]   else beliefs[speaker.movement]-=1
[22]  end-method

Listing 4: Changes in listing 1, non-deterministic behaviour and negative feedback.

3.4

We have also used this non-deterministic behaviour, together with negative-feedback, in the experiments reported next.

Movement strategies

4.1

In previous experiments, agents didn't have any moving strategy - their movements were completely random. In this section, we consider two different kinds of movement strategies that try to improve the speed of becoming uniform.

4.2

In the first strategy, the agent's choice of direction is proportional to its belief in the associated word, i.e. the higher the belief in a word, the higher the probability to choose that movement. The following is the pseudo-code for the method choose-movement, changed to reflect this strategy:

[6]   method choose-movement.
[7]   begin-method
[8]     rn    := choose a random (real) number between 0 and 1
[8.1]   total := beliefs[1]+beliefs[2]+beliefs[3]+beliefs[4]
[8.2]   if ( rn < belief[1]/total) then movement := 1
[8.3]   else if ( rn < (belief[1]+belief[2])/total ) then movement := 2
[8.4]   else if ( rn < (belief[1]+belief[2]+belief[3])/total ) then movement := 3
[8.5]   else movement := 4
[9]   end-method

Listing 5: Changes in listing 1, 'best known word' strategy.

4.3

This strategy greatly reduces the time taken to achieve uniformity. In 40 simulations with 1000 agents, we obtained vocabulary agreement at time 310 on average, with a standard deviation of 145. Figure 5 shows a simulation of 1000 agents.

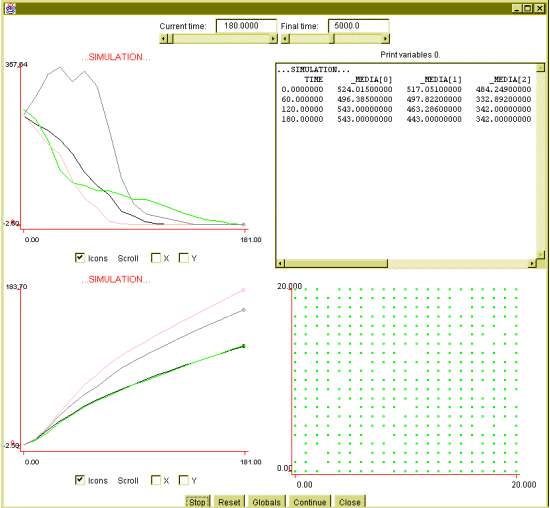
Figure 5:1000 agents simulation, 'best known word' strategy. Vocabulary achieved: 543, 443, 342, 862.

The time to consensus in this figure can be compared to that in figure 1 (deterministic case, no strategy). It can be noted that the belief curves are stratified. The higher belief value corresponds to the first word that reaches uniformity. This is due to the fact that this movement has been selected most frequently.

4.4

In the second strategy, the agent chooses the movement associated with the word in which it has least confidence (if there are two such words, a random word is chosen). After moving, each agent requests the associated word from the agents sharing the same position. In addition to a listen-to method, agents will have a speak-to method. For this strategy, Listing 1 has to be changed in the following way:

[6]   method choose-movement.
[7]   begin-method
[8]    movement := the position of the smallest element of the beliefs array
[9]   end-method
[22.1]  method speak-to ( Agent listener )
[22.2]  begin-method
[22.3]    listener.listen-to ( self )
[22.4]  end-method

Listing 6: Changes in listing 1, 'teach me' strategy.

The main simulation loop (listing 2) has also to be changed. Line 10 must be substituted as follows:

[6]      For each agent [a] in p:
[7]      begin-for
[8]        For each agent [b] in p:
[9]        begin-for
[10]         if (a <> b) then b.speak-to (a)

Listing 7: Changes in listing 1, 'teach me' strategy.

4.5

Figure 6 shows the simulation of a community of 1000 agents that use this strategy. In the picture, it can be seen that the beliefs associated with all the words grow at the same rate. This is due to the fact that each agent always requests and compares the word associated with its lowest belief, and therefore the degrees of belief for each agent tend to remain equal.

4.6

This strategy seems to be better than the basic strategy, but a little slower than the previous one, although it maintains belief indicators for all the words at similar values. In 40 experiments with 1000 agents, we obtained vocabulary agreement at average time 325, with a standard deviation of 105.

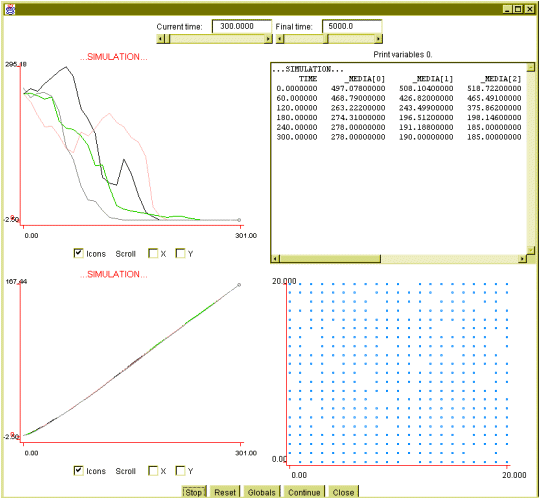
Figure 6:1000 agents simulation, 'teach me' strategy. Vocabulary achieved: 278, 190, 185, 2.

Roles

5.1

In these simulations, we introduce two new agent roles: sceptical and credulous agents. Credulous agents change their words more easily than normal agents, and the opposite happens with the sceptical.

In our first experiment we introduce sceptical agents. The probability for an agent to change its word in an encounter with another is:

p(change) = c × otherBelief/(ownBelief+otherBelief)

where ownBelief is the belief of the agent in its own word, and otherBelief is the belief of the other agent in its word. c is a constant for each agent that determines the degree of scepticallity of the agent and can have the following values:

• If c is 0, the agent never changes its word (completely sceptical).
• If c is less than 1, the agent is sceptical to some degree.
• If c is 1, the agent behaves as in previous simulations

5.2

To reflect sceptical behaviour, method listen-to in Listing 1 would have to be changed in the following way:

[14]  method listen-to ( Agent speaker )
[15]  begin-method
[16]   if ( words[speaker.movement] == speaker.words[speaker.movement] ) then beliefs[speaker.movement]+= 1.
[17]   else if (random()>c*beliefs[speaker.movement]/(beliefs[speaker.movement]+speaker.beliefs[speaker.movement])) then
[18]   begin-if
[19]     words[speaker.movement] := speaker.words[speaker.movement]
[20]     beliefs[speaker.movement] := speaker.beliefs[speaker.movement]
[21]   end-if
[21.1] else beliefs[speaker.movement]-=1
[22] end-method

Listing 8: Changes in listing 1, sceptic behaviour.

In addition, c is added as a new real attribute of each agent, and is initialized with a random number between 0 and 1.

5.3

In this kind of experiment, word uniformization takes a long time to appear, and in some cases it is not achieved. For low values of c, with 5% of the agents sceptical (i.e. 5% of them have a value of c between 0 and 0.5, and the others have c equal to 1), uniformization may not be achieved for any of the words (see figure 7).

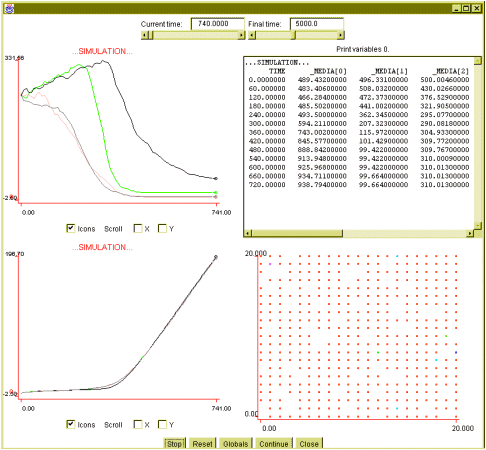
Figure 7: 1000 agents simulation, 5% are strongly sceptical, no uniformization takes place.

The belief indicators curve exhibits an interesting behaviour in these experiments. It reaches lower values than in the previous cases, and grows very little at the beginning, but after some time begins to grow faster. That time is associated with the decrease in the mean deviation of the words.

5.4

In our second experiment, we introduce credulous behaviour. The probability of an agent not changing its word is:

p(keep) = k × ownBelief/(ownBelief+otherBelief)
where k is a constant for each agent, with a value between 0 and 1. If k is zero, the agent always changes its word, and if k is less than 1, the agent is somewhat credulous. Changes would be similar to listing 8, but with a different condition in line 17.

5.5

Credulous agents exhibit a behaviour similar to sceptical agents. If a few of the total population are a little credulous, the uniformization process is slowed, but uniformization is reached. On the other hand, if some of them are strongly credulous, uniformization may never be reached.

As an example of this phenomenon, figure 8 shows a simulation of 600 agents, 50% of which are strongly credulous (50% have k between 0 and 0.5, and for the others k is 1). It can be observed that the belief indicator curves exhibit a similar behaviour as with sceptical agents, although the value reached is lower than in the previous cases: it grows very little at the beginning of the simulation, but later it grows faster. The change is associated with a strong displacement in the deviations.

5.6

We have also done experiments with different combinations of populations in the range from credulous to sceptical. No uniformization was reached in these cases.

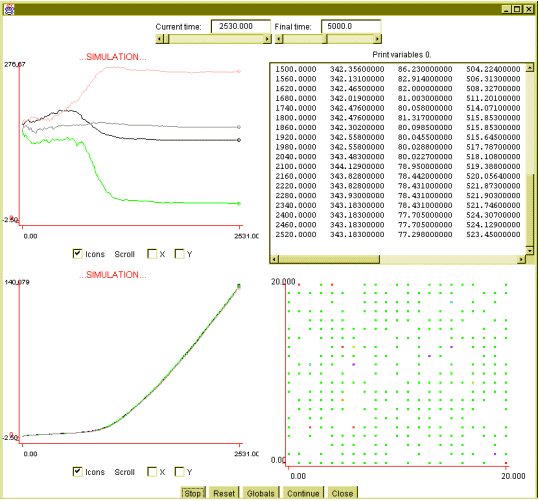
Figure 8: 600 agents simulation, 50% are strongly credulous, no uniformization takes place.

Conclusions and future work

6.1

We have presented a model that simulates the propagation of a vocabulary that names movements in a multi-agent environment. Agents have belief indicators associated with each word and trust their own word to a degree which depends on these indicators. Several trusting and moving strategies are studied. Vocabulary uniformization is reached in most simulations, but moving strategies accelerate the process (several statistical tests showed that using any of the two strategies is better than not using them, at a 99% level of confidence). Different agent roles are also examined: credulous and sceptical agents make the uniformization process slower, and sometimes a stationary state with no uniformization emerges.

6.2

These simulations may provide a tentative model of the way in which beliefs are transmitted in a closed group of people. In a situation where people have different beliefs, none of which is a priori better, a unique belief spreads and sometimes covers the whole population. Strongly sceptical or credulous agents prevent a single belief from spreading in the whole population, and a stable situation with several coexistent beliefs arises.

6.3

A different interpretation could set a parallel with ecosystems (Volterra, 1931), where each movement takes the place of a niche, and the actual words that represent the movement play the role of the species that compete for a given niche.

In the future, we plan to investigate different movement strategies, such as agents converging to the position where more individuals share the same word, which would probably result in a reinforcing of the agent beliefs. Other roles, such as lying or non-communicating agents can also be investigated. Other sources of negative feedback should be considered too, to model more realistic situations.

6.4

We are also considering adding artificial intelligence logic to our simulation language, in order to give the agents a more sophisticated way of reasoning.

Acknowledgements

This paper has been sponsored by the Spanish Interdepartmental Commission of Science and Technology (CICYT), project number TEL1999-0181

References

ALFONSECA, M., de Lara, J. , Pulido, E. 'Semiautomatic Generation of Web Courses by Means of an Object-Oriented Simulation Language', Simulation, special issue on Web-based Simulation, 73:1, pp. 5-12, Jul. 1999.

DAUTENHAHN, K. 1997. 'Ants don't have Friends - Thoughts on Socially Intelligent Agents', AAAI Technical Report FS 97-02, pp 22-27, Working Notes Socially Intelligent Agents, AAAI Fall Symposium, November 8-10 MIT, USA.

DAUTENHAHN, K. 1999. 'Embodiment and Interaction in Socially Intelligent Life-Like Agents'. In: C. L. Nehaniv (ed): Computation for Metaphors, Analogy and Agent, Springer Lecture Notes in Artificial Intelligence, Volume 1562, Springer, pp. 102-142.

DAWKINS, R. 1976. The Selfish Gene. New York, Oxford University Press.

DORIGO, M., Maniezzo, V. 1996. 'The Ant System: Optimization by a colony of cooperating agents'. IEEE Transactions on Systems, Man, and Cybernetics, Part-B, Vol.26, No.1, pp. 1-13.

EDMONDS, B. 1998. 'Modelling Socially Intelligent Agents'. Applied Artificial Intelligence, 12:677-699.

HALES, D. 1998. 'An Open Mind is not an Empty Mind: Experiments in the Meta-Noosphere'. Journal of Artificial Societies and Social Simulation vol. 1, no. 4, <https://www.jasss.org/1/4/2.html

HEGSELMANN, R., Flache, A. 1998. 'Understanding Complex Social Dynamics: A Plea for Cellular Automata Based Modelling'. Journal of Artificial Societies and Social Simulation. vol.1, no. 3 https://www.jasss.org/1/3/1.html.

HURFORD, J. 1999. 'Language Learning from Fragmentary Input'. In Proceedings of the AISB'99 Symposium on Imitation in Animals and Artifacts. Society for the Study of Artificial Intelligence and Simulation of behaviour. pp.121-129

KIRBY, S. 1998. 'Language evolution without natural selection: From vocabulary to syntax in a population of learners'. Edinburgh Occasional Paper in Linguistics EOPL-98-1

NEHANIV, C.L. 2000. 'The Making of Meaning in Societies: Semiotic & Information-Theoretic Background to the Evolution of Communication'. In Proceedings of the AISB Symposium: Starting from society - the application of social analogies to computational systems. pp. 73-84.

OLIPHANT, M. 1996.'The Dilemma of Saussurean Communication'. Biosystems, 37(1-2), pp. 31-38.

OPHIR, S. 1998. 'Simulating Ideologies'. Journal of Artificial Societies and Social Simulation vol. 1, no. 4, <https://www.jasss.org/1/4/5.html

RESNICK, M. 1999. Turtles, Termites, and Traffic Jams, explorations in massively parallel microworlds. MIT Press, 5th edition.

STEELS, L. 1995. 'Self-organizing vocabularies'. In C. Langton, editor. Proceedings of Alife V, Nara, Japan. 1996.

STEELS, L. 1996. 'A self-organizing spatial vocabulary'. Artificial Life Journal. 2(3) 1996.

STEELS, L. 1998. 'The Origins of Ontologies and Communication Conventions in Multi-Agent Systems'. Autonomous Agents and Multi-Agent Systems, 1, pp. 169-194.

VOLTERRA, V. 1931. Leçons sur la Théorie Mathématique de la Lutte pour la Vie, Gauthier-Villars, Paris.

WOOLDRIDGE, M,. Müller, J.P., Tambe, M. 1995. Intelligent Agents II. Agent Theories, Architectures and Languages. Springer.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 1999