Ramzi Suleiman and Ilan Fischer (2000)
When One Decides for Many: The Effect of Delegation Methods on Cooperation in Simulated Inter-group Conflicts
Journal of Artificial Societies and Social Simulation
vol. 3, no. 4,
<https://www.jasss.org/3/4/1.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 6-Jul-00 Accepted: 23-Sep-00 Published: 31-Oct-00
 Abstract
Abstract"It will sometimes happen that the minority are right, and the majority are wrong, but as soon as experience proves this to be the case, the minority will increase to a majority, and the error will reform itself by the tranquil operation of freedom of opinion and equality of rights" ( Thomas Paine, 1835, p.14).
| Table 1: Prisoner's Dilemma Payoff Matrix | ||
| Delegate B | ||
| C | D | |
| C | 5 , 5 | -10 , 10 |
| Delegate A | ||
| D | 10 , -10 | -5 , -5 |
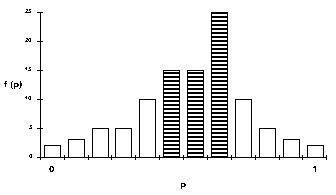
|
| Figure 1. The minimal winning coalition for a hypothetical distribution of cooperation |
To locate the group delegate, the simulation starts by finding all possible non-fragmented subgroups containing 51% or more of the population. The simulation proceeds by selecting the most compact one (i.e., the one with the minimal range on the p continuum). This is the dark shaded subgroup in Figure 1. This subgroup is sought as the minimal winning coalition in democratic elections held in this population, and its mean is sought as the elected group delegate. This delegate represents the entire group for the duration of a constituency period. After this period, new "elections" are held according to the procedure described above and a delegate with a new decision strategy is "elected".
| pi (t + 1) = pi (t) + K Od (t)/(pd (t)-pi (t)) | (1) |
where pi (t + 1) is the probability that the individual i will cooperate at period t+1, and K is a constant. In the reported simulations, the values for the outcome Od(t) are given by the matrix in Table 1. Accordingly, a delegated DM can either win 10 or 5 units, or lose 10 or 5 units. The numerical value for K in the reported simulations was K = 10-5. This ensured that incremental changes in individuals' attitudes were sufficiently small in order to achieve a gradual buildup of social influence.
|
if Od(t) >= 0 then pi (t + 1) = pi(t) if Od(t) < 0 THEN Pi (t + 1) = pi(t)+ m K Od(t) | (2) |
where m is a random parameter which assumes the values ± 1 with equal probabilities.
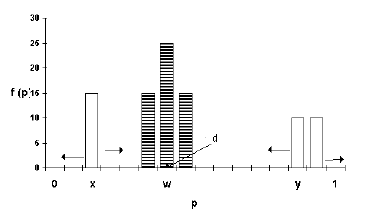
|
| Figure 2. The social influence process in a hypothetical population |
| For pi(t) > .975, pd(t) > .975, and Od(t) < 0 : If pi(t) > pd(t) then pi(t + 1) = pd(t) + K Od(t) | (3-a) |
Similarly, the lower boundary condition can be formalized as follows:
| For pi(t) > .025, pd(t) > .025, and Od(t) < 0 : If pi(t) < pd(t) then pi (t + 1) = pd(t) - K Od(t) | (3-b) |
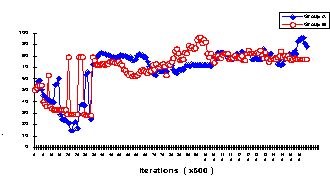
|
| Figure 3.1. The delegates rates of cooperation for a Cooperation-Cooperation pattern |
The maximum level of mutual cooperation obtained in the displayed result is quite impressive (about 80% for both delegates). In most other results the delegates' rates of cooperation were lower. For classification purposes, we decided to classify a pattern as a C-C pattern if it exhibited a clear and enduring pattern (for at least 5000 iterations) of mutual cooperation, and if the rate of cooperation of both delegates did not drop below the 51% threshold.
The corresponding intra-group dynamics for the result in Figure 3.1 is depicted in Figure 3.2. The vertical axis shows frequency distributions, and the horizontal axis shows the probabilities of cooperation given in equal intervals of 0.05 (denoted in the graphs by 0, 1, ..., 19).
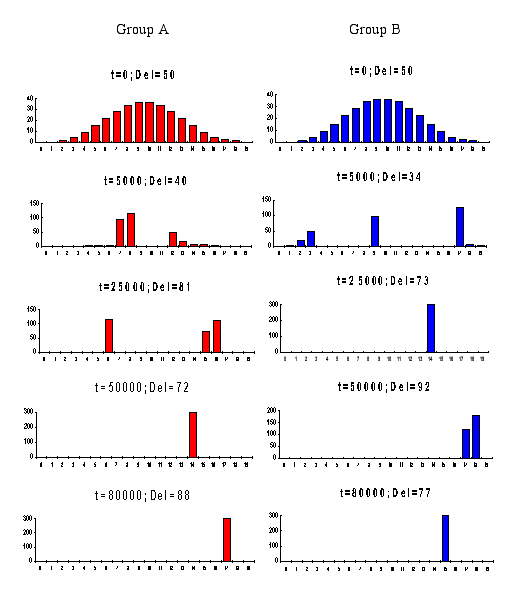
|
| Figure 3.2. The intra-group processes for a typical Cooperation-Cooperation pattern |
The figure shows that after some transitional period the two groups move towards high cooperation rates. When such a situation is reached, both delegates win (in expected values) and mutual cooperation is maintained.
|
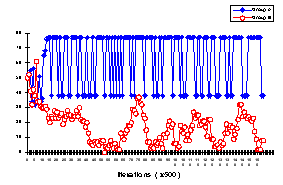
| Figure 4. The delegates' rates of cooperation for a typical Defection vs. Oscillation pattern |
This figure depicts the delegates' probabilities for cooperation as a function of the iterations. It clearly shows that after some transitional phase, a relatively stable steady state emerges in which group A's delegate continuously oscillates between high and low levels of cooperation, while group B's delegate converges slowly toward a very low level of cooperation.
|
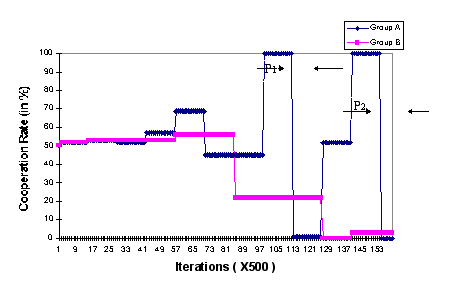
| Figure 5. The delegates' rates of cooperation for a simulation results with Cooperation vs. Defection phases |
|
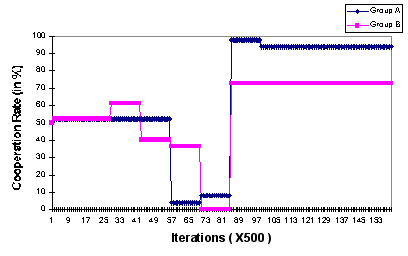
| Figure 6. The delegates' rates of cooperation for a simulation results with Mutual Defection phases |
|
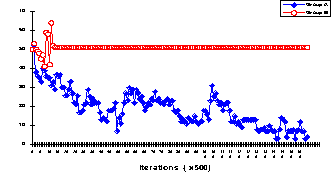
| Figure 7. The delegates' rates of cooperation for a typical Defection - 50% Cooperation pattern |
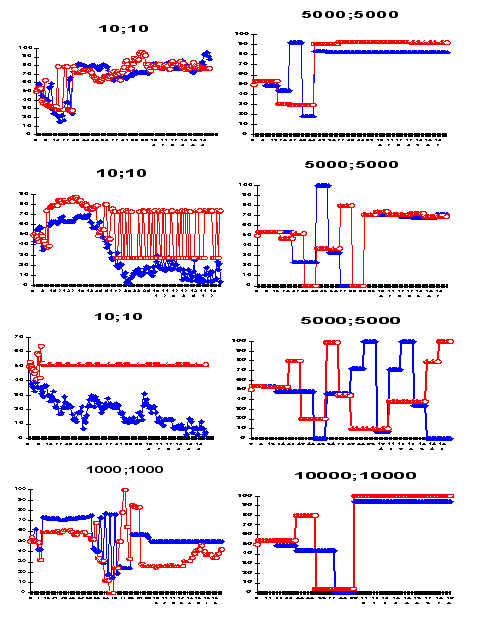
|
| Figure 8. Typical simulation results for some elections frequencies |
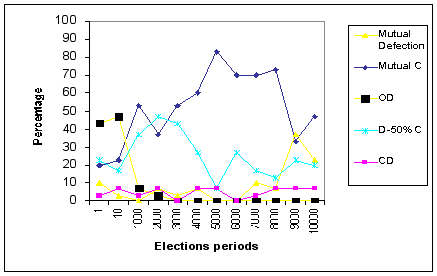
|
| Figure 9a. Frequencies of all Cooperation patterns (in %) at the end of 80,000 iterations under the Minimal Wining Coalition method, for each elections condition |
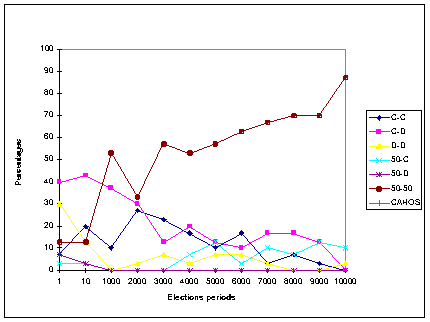
|
| Figure 9b. Frequencies of all Cooperation patterns (in %) at the end of 80,000 iterations under the Mean Representation method, for each elections condition |
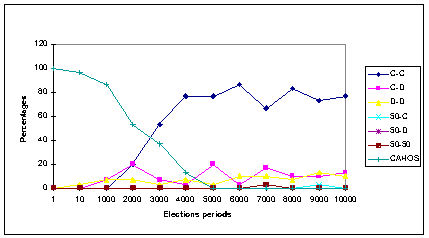
|
| Figure 9c. Frequencies of all Cooperation patterns (in %) at the end of 80,000 iterations under the Random Representation method, for each elections condition |
|
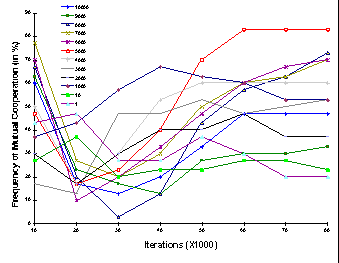
| Figure 10a. Frequencies of the Mutual Cooperation patterns (in %) under the Minimal Wining Coalition procedure for each elections condition |
|
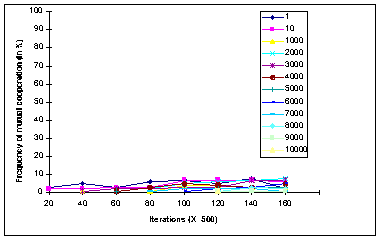
| Figure 10b. Frequencies of the Mutual Cooperation patterns (in %) under the Mean Attitude Representation procedure for each elections condition |
|
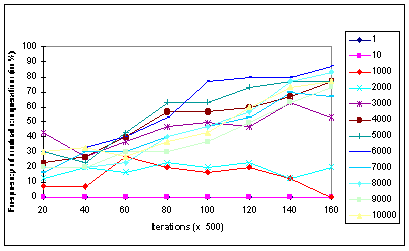
| Figure 10c. Frequencies of the Mutual Cooperation patterns (in %) under the Random Attitude Representation procedure for each elections condition |
| f(p) = pu (1-p) v / B(u,v) | if 0 <= p <= 1 |
| 0 | Otherwise |
2 The parameters of the beta function for producing this distributions were u = v = 5 for the two groups. Moreover, in all reported simulations the continuous beta functions were approximated by discrete functions with equal intervals of D = 0.05.
3 A non-fragmented group is one that is defined over a continuous segment of the cooperativeness range.
4 The durability of a given pattern, as defined here, does not imply that a static, or dynamic, equilibrium was reached.
AXELROD, R. (1984). The Evolution of Cooperation. New York: Basic Books.
BRAMS, S. (1975). Game Theory and Politics. New York: Free Press.
DERMAN, C., Gleser, L. J., and Olkin, I. (1973). A Guide to Probability Theory and Application.New York: Holt, Rinehart, and Winston.
FISCHER, I. Suleiman, R., (1997). "Mutual Cooperation in a Simulated Inter-group Conflict". Journal of Conflict Resolution 41 (4), 483-508.
JOHNSON, N. L., and Kotz, S. (1969). Distributions in Statistics. Boston, MA: Houghton Mifflin.
LATANÉ, B. (1981). "The psychology of social impact". American Psychologist 36, 343-365.
MILL, J. (1828). Essay on Government (new edition 1955). New York: Bobbs-Merrill.
NOWAK, A., Szamrej, J., and Latané, B. (1990). "From private attitude to public opinion: A dynamic theory of social impact". Psychological Review 97 (3), 362-374.
PAINE, Thomas. (1793). The Catachism of Man. London.
PAINE, T. (1835): Dissertation on First principles of government. James Watson, London
ROUSSEAU, J. J. (1762). The Social Contract (new edition 1954) Illinois: Henry Regnery.
SCHELLING, T. (1960). The Strategy of Conflict. Cambridge, MA: Harvard University Press.
SULEIMAN, R., and Fischer, I. (1996). "The Evolution of Cooperation in a Simulated Inter-group Conflict", in W. B. G. Liebrand, and D. M. Messick (eds.). Frontiers in Social Dilemmas Research. (pp. 419-438). Berlin: Springer-Verlag.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999