Evelien P.H. Zeggelink, Henk de Vos and Donald Elsas (2000)
Reciprocal altruism and group formation: The degree of segmentation of reciprocal altruists who prefer 'old-helping-partners'
Journal of Artificial Societies and Social Simulation
vol. 3, no. 3,
<https://www.jasss.org/3/3/1.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 1-Mar-00 Accepted: 20-May-00 Published: 30-Jun-00
 Abstract
Abstract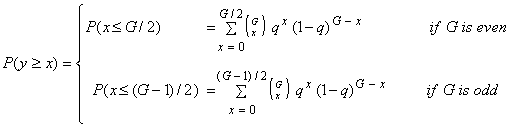 |
(3.1) |
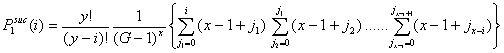 |
(3.2) |
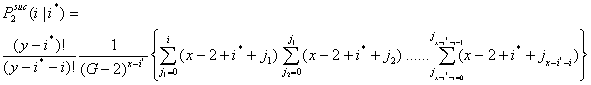 |
(3.3) |
 |
(3.4) |
| Table 3.1:Probability that all x actors in distress in a group of size G find a helping partner | |||||||||||
| x | |||||||||||
| G | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1.00 | ||||||||||
| 2 | 1.00 | 1.00 | |||||||||
| 3 | 1.00 | 1.00 | |||||||||
| 4 | 1.00 | 1.00 | 1.00 | ||||||||
| 5 | 1.00 | 1.00 | 1.00 | ||||||||
| 6 | 1.00 | 1.00 | 1.00 | .464 | |||||||
| 7 | 1.00 | 1.00 | 1.00 | .693 | |||||||
| 8 | 1.00 | 1.00 | 1.00 | .810 | .208 | ||||||
| 9 | 1.00 | 1.00 | 1.00 | .875 | .405 | ||||||
| 10 | 1.00 | 1.00 | 1.00 | .914 | .555 | .091 | |||||
| 11 | 1.00 | 1.00 | 1.00 | .938 | .663 | .218 | |||||
| 12 | 1.00 | 1.00 | 1.00 | .954 | .740 | .343 | .039 | ||||
| 13 | 1.00 | 1.00 | 1.00 | .965 | .797 | .453 | .111 | ||||
| 14 | 1.00 | 1.00 | 1.00 | .973 | .838 | .545 | .198 | .017 | |||
| 15 | 1.00 | 1.00 | 1.00 | .978 | .870 | .621 | .288 | .054 | |||
| 16 | 1.00 | 1.00 | 1.00 | .982 | .893 | .682 | .373 | .108 | .007 | ||
| 17 | 1.00 | 1.00 | 1.00 | .986 | .912 | .731 | .450 | .172 | .026 | ||
| 18 | 1.00 | 1.00 | 1.00 | .988 | .926 | .772 | .518 | .240 | .057 | .003 | |
| 19 | 1.00 | 1.00 | 1.00 | .990 | .938 | .805 | .578 | .308 | .099 | .012 | |
| 20 | 1.00 | 1.00 | 1.00 | .991 | .947 | .832 | .629 | .372 | .148 | .029 | .001 |
| Table 3.2:Probability that x actors are in distress and find help in group of size G, (q = 0.05) | |||||||||||||||||||||||
| x G | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| 0 | 1.0 | 1.0 | |||||||||||||||||||||
| 1 | .95 | .00 | .95 | ||||||||||||||||||||
| 2 | .90 | .10 | .00 | 1.0 | |||||||||||||||||||
| 3 | .86 | .14 | .00 | .00 | 1.0 | ||||||||||||||||||
| 4 | .81 | .17 | .01 | .00 | .00 | .99 | |||||||||||||||||
| 5 | .77 | .20 | .02 | .00 | .00 | .00 | .99 | ||||||||||||||||
| 6 | .74 | .23 | .03 | .00 | .00 | .00 | .00 | 1.0 | |||||||||||||||
| 7 | .70 | .26 | .04 | .00 | .00 | .00 | .00 | .00 | 1.0 | ||||||||||||||
| 8 | .66 | .28 | .05 | .01 | .00 | .00 | .00 | .00 | .00 | 1.0 | |||||||||||||
| 9 | .63 | .30 | .06 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | ||||||||||||
| 10 | .60 | .32 | .07 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | |||||||||||
| 11 | .57 | .33 | .09 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | ||||||||||
| 12 | .54 | .34 | .10 | .02 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | |||||||||
| 13 | .51 | .35 | .11 | .02 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | ||||||||
| 14 | .49 | .36 | .12 | .03 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | |||||||
| 15 | .46 | .37 | .13 | .03 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | ||||||
| 16 | .44 | .37 | .14 | .04 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | |||||
| 17 | .42 | .37 | .16 | .04 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | ||||
| 18 | .40 | .38 | .17 | .05 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | |||
| 19 | .38 | .38 | .18 | .05 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | ||
| 20 | .36 | .38 | .19 | .06 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | |
| Table 3.3:Probability that x actors are in distress and find help in group of size G, (q = 0.10) | |||||||||||||||||||||||
| x G | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| 0 | 1.0 | 1.0 | |||||||||||||||||||||
| 1 | .90 | .00 | .90 | ||||||||||||||||||||
| 2 | .81 | .18 | .00 | .99 | |||||||||||||||||||
| 3 | .73 | .24 | .00 | .00 | .97 | ||||||||||||||||||
| 4 | .66 | .29 | .05 | .00 | .00 | 1.0 | |||||||||||||||||
| 5 | .59 | .33 | .07 | .00 | .00 | .00 | .99 | ||||||||||||||||
| 6 | .53 | .35 | .10 | .00 | .00 | .00 | .00 | .98 | |||||||||||||||
| 7 | .48 | .37 | .12 | .01 | .00 | .00 | .00 | .00 | .98 | ||||||||||||||
| 8 | .43 | .38 | .15 | .02 | .00 | .00 | .00 | .00 | .00 | .98 | |||||||||||||
| 9 | .39 | .39 | .17 | .04 | .00 | .00 | .00 | .00 | .00 | .00 | .99 | ||||||||||||
| 10 | .35 | .39 | .19 | .05 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .99 | |||||||||||
| 11 | .31 | .38 | .21 | .07 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .98 | ||||||||||
| 12 | .28 | .38 | .23 | .09 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .99 | |||||||||
| 13 | .25 | .37 | .24 | .10 | .02 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .98 | ||||||||
| 14 | .23 | .36 | .26 | .11 | .03 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | |||||||
| 15 | .21 | .34 | .27 | .13 | .03 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .99 | ||||||
| 16 | .19 | .33 | .27 | .14 | .04 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .98 | |||||
| 17 | .17 | .32 | .28 | .16 | .05 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .99 | ||||
| 18 | .15 | .30 | .28 | .17 | .06 | .02 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .99 | |||
| 19 | .14 | .29 | .29 | .18 | .08 | .02 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | 1.0 | ||
| 20 | .12 | .27 | .29 | .19 | .09 | .02 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .99 | |
| Table 3.4:Probability that x actors are in distress and find help in group of size G, (q = 0.20) | |||||||||||||||||||||||
| x G | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| 0 | 1.0 | 1.0 | |||||||||||||||||||||
| 1 | .80 | .00 | .80 | ||||||||||||||||||||
| 2 | .64 | .32 | .00 | .96 | |||||||||||||||||||
| 3 | .51 | .38 | .00 | .00 | .89 | ||||||||||||||||||
| 4 | .41 | .41 | .15 | .00 | .00 | .87 | |||||||||||||||||
| 5 | .33 | .41 | .20 | .00 | .00 | .00 | .94 | ||||||||||||||||
| 6 | .26 | .39 | .25 | .04 | .00 | .00 | .00 | .94 | |||||||||||||||
| 7 | .21 | .37 | .28 | .08 | .00 | .00 | .00 | .00 | .94 | ||||||||||||||
| 8 | .17 | .34 | .29 | .12 | .01 | .00 | .00 | .00 | .00 | .93 | |||||||||||||
| 9 | .13 | .30 | .30 | .16 | .03 | .00 | .00 | .00 | .00 | .00 | .92 | ||||||||||||
| 10 | .11 | .27 | .30 | .18 | .05 | .00 | .00 | .00 | .00 | .00 | .00 | .91 | |||||||||||
| 11 | .09 | .24 | .30 | .21 | .07 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .92 | ||||||||||
| 12 | .07 | .21 | .28 | .23 | .10 | .02 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .91 | |||||||||
| 13 | .05 | .18 | .27 | .24 | .12 | .03 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .89 | ||||||||
| 14 | .04 | .15 | .25 | .24 | .14 | .05 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .88 | |||||||
| 15 | .04 | .13 | .23 | .24 | .17 | .06 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .88 | ||||||
| 16 | .03 | .11 | .21 | .25 | .18 | .08 | .02 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .88 | |||||
| 17 | .02 | .10 | .19 | .24 | .19 | .10 | .03 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .88 | ||||
| 18 | .02 | .08 | .17 | .23 | .20 | .12 | .04 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .87 | |||
| 19 | .01 | .07 | .15 | .22 | .21 | .13 | .06 | .01 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .86 | ||
| 20 | .01 | .06 | .14 | .21 | .21 | .14 | .07 | .02 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .00 | .86 | |
| (4.1) |
| Qb = Fb + Fb + 1 +......+ F¥ = 1 - (F1 + F2 +......+ Fb - 1) | (4.2) |
| (4.3) |
|
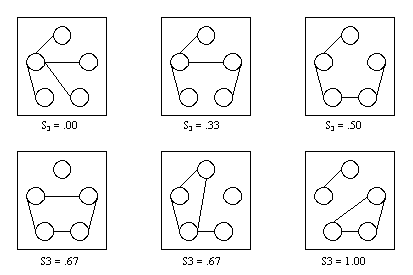
| Figure 4.1. All graphs on 5 nodes with 4 edges |
It illustrates that the degree of segmentation (even for an equal number of edges) may vary between S3 = .00 and S3 = 1.00. The more separated the nodes in the graph get, the higher the degree of segmentation, with its maximum for a complete separation into cliques.
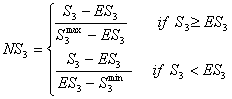 |
(4.4) |
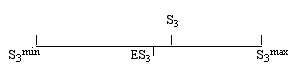
Where S3 could vary between 0 and 1, NS3 can now vary between the values -1 and 1. When S3 is larger than ES3 , NS3 is larger than 0, and closer to 1 as S3 gets closer to S3 max. A positive value of S3 means that the graph is more segmented than could be expected on the basis of a random distribution of the same number of edges among the same number of nodes. A value of NS3 smaller than 0, means that the graphs is less segmented than a random graph. NS3 = 1 means that the graphs is maximally segmented, NS3 = -1 means that the graph is minimally segmented. Note that if S3 < 1, NS3 can still equal 1. This is the case if S3 = S3 max. If S3 = 1, NS3 = 0 or NS3 = 1. If NS3 = 1, this does not imply that S3 = 1. S3 can be smaller.
| Table 5.1:The number of pairs or the maximal number of relationships in networks of size n | |||
| n | maximal number of relationships = n(n - 1) /2 | n | maximal number of relationships = n(n - 1) /2 |
| 0 | 0 | ||
| 1 | 0 | 11 | 55 |
| 2 | 1 | 12 | 66 |
| 3 | 3 | 13 | 78 |
| 4 | 6 | 14 | 91 |
| 5 | 10 | 15 | 105 |
| 6 | 15 | 16 | 120 |
| 7 | 21 | 17 | 136 |
| 8 | 28 | 18 | 153 |
| 9 | 36 | 19 | 171 |
| 10 | 45 | 20 | 190 |
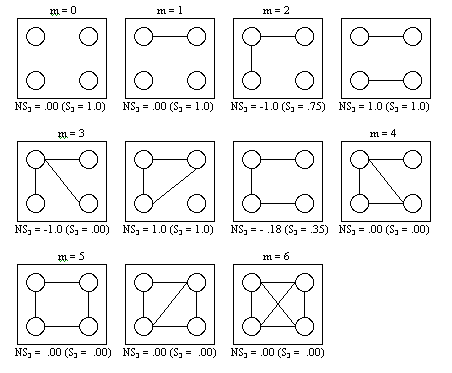
|
| Figure 6.1. All different networks of 4 actors |
Only for two values of m, m = 2 or m = 3, non-zero values of NS3 exist. For m = 2, S3 = 0.75 or S3 = 1.00, corresponding by definition to NS3 = -1 and NS3 = 1, respectively. When m = 3, S3 = 0.00, S3 = 1.00, or S3 = 0.35, corresponding to NS3 = -1.00, NS3 = 1.00, and NS3 = -0.18, respectively.
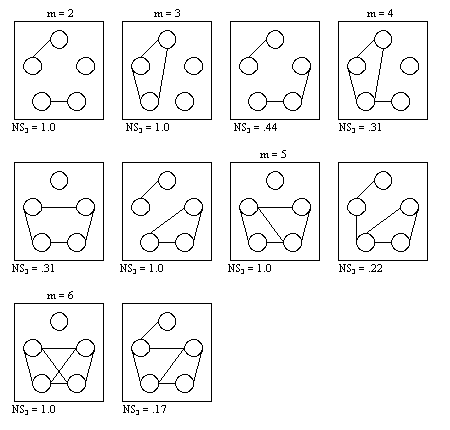
|
| Figure 6.2. All networks of 5 actors with a positive normalized segmentation index |
The degree of normalization has its own interpretation space. If we consider a network to be existing of very close(d) subgroups without any links between the groups, than only NS3 = 1 would suffice. However, for all networks of size n = 5 with a positive normalized segmentation index, it can be said that there has been at least some process of group formation. Beyond m = 6 relationships however, no positive normalized values of the segmentation index are possible (NS3 = 0 by definition).
| Table 6.1a: Normalized degree of segmentation for different social populations n = 4 to n = 10 | |||||||||||||||
| n | |||||||||||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||
| N | |||||||||||||||
| m | 10 | 20 | 10 | 0 | 10 | 20 | 10 | 20 | 10 | 20 | 10 | 20 | 10 | 20 | |
| 2 | -0.02 | -0.17 | -0.05 | 0.28 | 0.32 | 0.19 | 0.65 | 0.46 | 0.72 | 0.50 | 0.48 | 0.52 | 0.55 | 0.65 | |
| 3 | -0.19 | -0.13 | 0.17 | 0.13 | 0.31 | 0.29 | 0.30 | 0.29 | 0.54 | 0.38 | 0.20 | 0.40 | 0.28 | 0.23 | |
| 4 | 0.00 | 0.00 | 0.00 | 0.00 | 0.17 | 0.17 | 0.19 | 0.22 | 0.19 | 0.34 | 0.24 | 0.32 | 0.26 | 0.34 | |
| 5 | 0.00 | 0.00 | -0.31 | -0.37 | 0.01 | 0.15 | 0.09 | 0.18 | 0.24 | 0.22 | 0.35 | 0.28 | 0.25 | 0.30 | |
| 6 | 0.00 | -0.17 | -0.87 | -0.06 | -0.10 | 0.04 | 0.08 | 0.21 | 0.17 | 0.19 | 0.23 | 0.26 | 0.32 | ||
| 7 | 0.00 | -0.28 | -0.29 | 0.00 | 0.02 | 0.08 | 0.11 | 0.17 | 0.17 | 0.13 | 0.16 | ||||
| 8 | 0.00 | -0.10 | 0.17 | -0.19 | -0.07 | 0.01 | 0.06 | 0.08 | 0.09 | 0.15 | 0.18 | ||||
| 9 | -1.00 | -1.00 | -0.10 | -0.09 | 0.03 | -0.03 | 0.05 | 0.08 | 0.12 | 0.12 | |||||
| 10 | -1.00 | -0.36 | -0.39 | -0.17 | -0.17 | -0.02 | 0.01 | 0.06 | 0.07 | ||||||
| 11 | 0.00 | -1.00 | -0.27 | 0.10 | 0.10 | 0.06 | 0.06 | 0.05 | |||||||
| 12 | -0.06 | -0.22 | -0.05 | -0.08 | 0.00 | 0.06 | |||||||||
| 13 | 0.04 | -0.61 | -0.20 | -0.01 | -0.03 | ||||||||||
| 14 | -1.00 | -0.33 | -0.21 | -0.06 | |||||||||||
| 15 | -0.09 | -0.12 | 0.11 | ||||||||||||
| 16 | 0.09 | -0.54 | |||||||||||||
| 17 | -0.43 | ||||||||||||||
| .. | |||||||||||||||
| Table 6.1b: Normalized degree of segmentation for different social populations n =11 to n = 20 | |||||||||||
| n | |||||||||||
| m | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 2 | -0.33 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||||
| 3 | 0.38 | 0.67 | 0.33 | 1.00 | 1.00 | 0.00 | 0.00 | -0.13 | |||
| 4 | 0.75 | 0.34 | 0.35 | 0.42 | 0.78 | 0.83 | 0.75 | 0.83 | 0.87 | 1.00 | |
| 5 | 0.52 | 0.30 | 0.41 | 0.21 | 0.42 | 0.71 | 0.61 | 0.52 | 0.62 | 0.83 | |
| 6 | 0.28 | 0.35 | 0.30 | 0.19 | 0.23 | 0.31 | 0.24 | 0.39 | 0.40 | 0.60 | |
| 7 | 0.14 | 0.34 | 0.39 | 0.36 | 0.25 | 0.33 | 0.25 | 0.28 | 0.23 | 0.35 | |
| 8 | 0.29 | 0.15 | 0.16 | 0.22 | 0.21 | 0.34 | 0.25 | 0.34 | 0.25 | 0.43 | |
| 9 | 0.20 | 0.16 | 0.23 | 0.16 | 0.23 | 0.29 | 0.25 | 0.31 | 0.22 | 0.35 | |
| 10 | 0.19 | 0.13 | 0.24 | 0.21 | 0.34 | 0.27 | 0.22 | 0.28 | 0.21 | 0.25 | |
| 11 | 0.14 | 0.09 | 0.21 | 0.19 | 0.23 | 0.26 | 0.31 | 0.21 | 0.26 | 0.25 | |
| 12 | 0.15 | 0.12 | 0.11 | 0.19 | 0.17 | 0.24 | 0.30 | 0.28 | 0.30 | 0.39 | |
| 13 | 0.03 | 0.09 | 0.14 | 0.12 | 0.14 | 0.22 | 0.16 | 0.18 | 0.21 | 0.21 | |
| 14 | 0.01 | 0.09 | 0.08 | 0.13 | 0.10 | 0.14 | 0.14 | 0.19 | 0.22 | 0.23 | |
| 15 | 0.02 | 0.02 | 0.08 | 0.15 | 0.10 | 0.17 | 0.09 | 0.20 | 0.23 | 0.22 | |
| 16 | -0.07 | 0.01 | 0.08 | 0.06 | 0.18 | 0.16 | 0.16 | 0.16 | 0.12 | 0.27 | |
| 17 | -0.10 | 0.02 | 0.08 | 0.06 | 0.08 | 0.10 | 0.15 | 0.14 | 0.20 | ||
| 18 | -0.29 | -0.01 | 0.06 | 0.02 | 0.13 | 0.14 | 0.14 | 0.20 | 0.15 | ||
| 19 | 0.00 | 0.03 | 0.08 | 0.14 | 0.10 | 0.15 | 0.15 | 0.16 | |||
| 20 | 0.08 | 0.05 | 0.06 | 0.11 | 0.11 | 0.14 | 0.22 | ||||
| 21 | -0.05 | 0.02 | 0.03 | 0.11 | 0.08 | 0.04 | 0.13 | ||||
| 22 | 0.00 | 0.00 | 0.07 | 0.11 | 0.09 | 0.08 | 0.00 | ||||
| 23 | - 0.12 | 0.05 | 0.02 | 0.03 | 0.08 | 0.17 | 0.06 | ||||
| 24 | -0.02 | 0.09 | 0.06 | 0.06 | 0.02 | 0.08 | |||||
| 25 | 0.00 | -0.04 | 0.03 | 0.13 | 0.08 | ||||||
| 26 | -0.04 | 0.22 | 0.00 | 0.01 | 0.18 | ||||||
| 27 | 0.03 | 0.03 | |||||||||
| 28 | |||||||||||
| 29 | 0.15 | ||||||||||
| 30 | |||||||||||
| 31 | 0.06 | ||||||||||
| 32 | 0.10 | ||||||||||
| .. | |||||||||||
Before we derive the desired probability we first present an example of the choice process in the first interval.
Assume the total number of actors in the population is six (G = 6). Let the number of actors in distress be three (x = 3). The number of y-actors thus also equals three (y = 3). All x-actors will choose among all other actors. Since every actor x has (G-1) = 5 alternatives, the total number of possible choices is (G-1)x = 53 = 125. All these possibilities are given in Table A.1. The columns (1) and (1a) give the number of the possibility. The columns (2) and (2a), (3) and (3a), (4) and (4a) present the choice of the first, second, and third x-actor respectively. The columns (5) and (5a) show the number of successful actors. From these 125 possibilities, 8 choice combinations (1, 2, 6, 7, 11, 12, 16, 17) lead to no successes. In that case, all x-actors choose on of the other x-actors. 57 choice combinations lead to 1 success. In that case, only one of the x-actors chooses a y-actor, or two or three x-actors choose one and the same y-actor. 54 choice combinations lead to 2 successes and only 6 choice combinations (70, 74, 90, 98, 114, 118) lead to three successes. In the latter case, all three x-actors choose a unique y-actor. As such, the probability of no success is 8/125 = .064, the probability of 1 successful actor is 57/125 = .456, the probability of two successes is 54/125 = .432, and the probability of three successes is 6/125 = .048.
Table A.1: All potential outcomes of choices of 3 x-actors in a group of 6 actors, first interval (1)
out-come(2)
choice x1(3)
choice x2(4)
choice x3(5)
#
successful actors(1)
out-come(2a)
choice x1(3a)
choice x2(4a)
choice x3(5a)
#
successful actors1 x2 x1 x1 0 36 x3 y1 x1 1 2 x2 x1 x2 0 37 x3 y1 x2 1 3 x2 x1 y1 1 38 x3 y1 y1 1 4 x2 x1 y2 1 39 x3 y1 y2 2 5 x2 x1 y3 1 40 x3 y1 y3 2 6 x2 x3 x1 0 41 x3 y2 x1 1 7 x2 x3 x2 0 42 x3 y2 x2 1 8 x2 x3 y1 1 43 x3 y2 y1 2 9 x2 x3 y2 1 44 x3 y2 y2 1 10 x2 x3 y3 1 45 x3 y2 y3 2 11 x3 x1 x1 0 46 x3 y3 x1 1 12 x3 x1 x2 0 47 x3 y3 x2 1 13 x3 x1 y1 1 48 x3 y3 y1 2 14 x3 x1 y2 1 49 x3 y3 y2 2 15 x3 x1 y3 1 50 x3 y3 y3 1 16 x3 x3 x1 0 51 y1 x1 x1 1 17 x3 x3 x2 0 52 y1 x1 x2 1 18 x3 x3 y1 1 53 y1 x1 y1 1 19 x3 x3 y2 1 54 y1 x1 y2 2 20 x3 x3 y3 1 55 y1 x1 y3 2 21 x2 y1 x1 1 56 y1 x3 x1 1 22 x2 y1 x2 1 57 y1 x3 x2 1 23 x2 y1 y1 1 58 y1 x3 y1 1 24 x2 y1 y2 2 59 y1 x3 y2 2 25 x2 y1 y3 2 60 y1 x3 y3 2 26 x2 y2 x1 1 61 y1 y1 x1 1 27 x2 y2 x2 1 62 y1 y1 x2 1 28 x2 y2 y1 2 63 y1 y1 y1 1 29 x2 y2 y2 1 64 y1 y1 y2 2 30 x2 y2 y3 2 65 y1 y1 y3 2 31 x2 y3 x1 1 66 y1 y2 x1 2 32 x2 y3 x2 1 67 y1 y2 x2 2 33 x2 y3 y1 2 68 y1 y2 y1 2 34 x2 y3 y2 2 69 y1 y2 y2 2 35 x2 y3 y3 1 70 y1 y2 y3 3
Table A.1 (continued): All potential outcomes of choices of 3 x-actors in a group of 6 actors (1)
out-come(2)
choice x1(3)
choice x2(4)
choice x3(5)
#
successful actors(1)
out-come(2a)
choice x1(3a)
choice x2(4a)
choice x3(5a)
#
successful actors71 y1 y3 x1 2 101 y3 x1 x1 1 72 y1 y3 x2 2 102 y3 x1 x2 1 73 y1 y3 y1 2 103 y3 x1 y1 2 74 y1 y3 y2 3 104 y3 x1 y2 2 75 y1 y3 y3 2 105 y3 x1 y3 1 76 y2 x1 x1 1 106 y3 x3 x1 1 77 y2 x1 x2 1 107 y3 x3 x2 1 78 y2 x1 y1 2 108 y3 x3 y1 2 79 y2 x1 y2 1 109 y3 x3 y2 2 80 y2 x1 y3 2 110 y3 x3 y3 1 81 y2 x3 x1 1 111 y3 y1 x1 2 82 y2 x3 x2 1 112 y3 y1 x2 2 83 y2 x3 y1 2 113 y3 y1 y1 2 84 y2 x3 y2 1 114 y3 y1 y2 3 85 y2 x3 y3 2 115 y3 y1 y3 2 86 y2 y1 x1 2 116 y3 y2 x1 2 87 y2 y1 x2 2 117 y3 y2 x2 2 88 y2 y1 y1 2 118 y3 y2 y1 3 89 y2 y1 y2 2 119 y3 y2 y2 2 90 y2 y1 y3 3 120 y3 y2 y3 2 91 y2 y2 x1 1 121 y3 y3 x1 1 92 y2 y2 x2 1 122 y3 y3 x2 1 93 y2 y2 y1 2 123 y3 y3 y1 2 94 y2 y2 y2 1 124 y3 y3 y2 2 95 y2 y2 y3 2 125 y3 y3 y3 1 96 y2 y3 x1 2 97 y2 y3 x2 2 98 y2 y3 y1 3 99 y2 y3 y2 2 100 y2 y3 y3 2
Now let p1suc(i) be the probability that, in the first interval of a period, i of the x-actors are successful in finding an helping partner among the y-actors. If x individuals are in distress, the number of successful x-individuals, i, can vary from 0 to x. It is self-evident that Pisuc(i) depends on x and y:
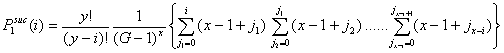 |
(A.1) |
This probability in (A.1) is derived and defined as the number of successful outcomes divided by the total number of ways ((G-1)x) in which x searching actors can choose among all other (G-1) actors. The first fraction in (A.1) is the number of possible ways in which i of the x actors in distress can be successful. This means that it represents the number of distinct ways that these i x-actors can choose i different y-actors: y such actors exist who can provide help. Each actor in distress chooses, in order to be successful, one single and unique y-actor. Suppose that i = 1, this means that the chosen y-actor (no matter how many x-actors choose this y-actor) can be either of the y y-actors (y = y!/ (y - 1)!). Therefore the term within brackets is multiplied by the fraction y!/(y - i)!
The product of sums within brackets represents the ways in which the choices of the (x-i) unsuccessful actors can be arranged over the other (G-1-i) actors.[20] Since these actors are unsuccessful, they choose either from the other actors in distress (x-1 others), or they choose one of the y-actors (i are 'occupied') that has been asked by a successful x-actor already. The term within the first summation sign relates to the first unsuccessful actor, and based on his choice, choices of the other actors are 'restricted' in such a way that double patterns are avoided. Within these summations jk controls for the number of y-actors that has been chosen already. It should be noted that there is a new second sum for every step of the iterator of the first sum, and so forth.
If i = 0 for example, none of the actors in distress is successful. This means that all x actors choose among themselves (and for the product within brackets only terms with j1 = j2 = ...jx = 0 will occur). If i = 1, all (x-1) unsuccessful actors choose either the same y that the successful actor chooses, or they choose one of the other x actors. This returns in the summations dependent on whether the first not successful actor chooses that y-actor (j1 = 1) or not.
Returning to our example, we fill in x = 3, y = 3 and G = 6 and obtain:
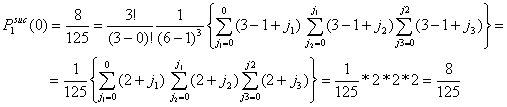
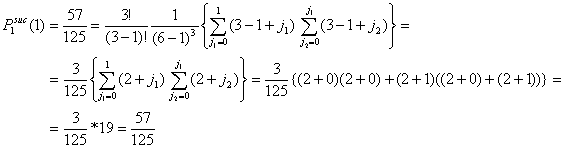
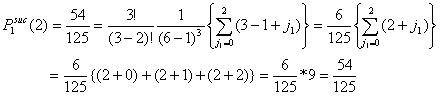
![]()
All actors that are not successful in the first interval however have two additional chances to find a helping y-actor. Equation (A.1) thus needs to be extended for those cases in which less than x actors are successful. What happened when i is smaller than x? This means that x-i actors either asked another x-actor for help or asked one of the i y-actors that was simultaneously (in the same first interval) asked by another x-actor (who got preferred randomly). Every unsuccessful x-actor knows that he should not ask that actor again (actors not in distress can help only one actor in a period). The unsuccessful x-actors however still do not know who the actors in distress, or the actors not in distress are.[21]
In general, this translates for the second interval only for a change in the parameter values of (A.1). Let P2suc(i|i*) be the probability that i x-actors are successful in the second interval given that i* x-actors were successful in the first interval. Now, i can vary between 0 and x - i*. Going from Equation (A.1) to Equation (A.2), the number of searching actors changes from x to x-i*, the number of available helping y-actors changes from y to y - i*, and the number of possibilities changes from (G-1)x to (G-2)x-i* because every unsuccessful x-actor will not return to that actor he asked for help in the first time interval. All x - i* actors can still ask all other x-actors, and also all i* y-actors that cannot provide help anymore.
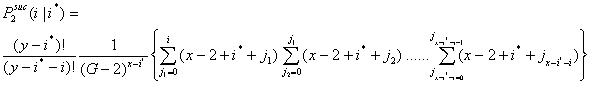 |
(A.2) |
In a similar way, the probability for i successful actors in the third interval can be derived, resulting in Equation (A.3). Let P3suc(i|i*) be the probability that i x-actors are successful in the third interval given that a total of i* x-actors were successful in the first and second interval.
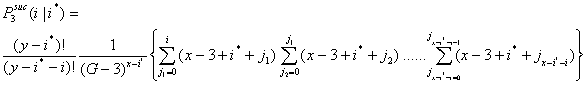 |
(A.3) |
| Table B1: S3 for networks of 4 actors (n = 4) with different densities | ||||||||||
| a | N = 10 | |||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| m | den | q | ||||||||
| 0.20 | 0.10 | 0.05 | tot | |||||||
| S3 | # | S3 | # | S3 | # | S3 | NS3 | # | ||
| 0 | 0.00 | 1.00 (.00) | 2 | 1.00 (.00) | 22 | 1.00 (.00) | 0.00 (.00)° | 24 | ||
| 1 | 0.17 | 1.00 (.00) | 4 | 1.00 (.00) | 14 | 1.00 (.00) | 47 | 1.00 (.00) | 0.00 (.00) | 65 |
| 2 | 0.33 | 0.95 (.10) | 15 | 0.87 (.13) | 36 | 0.83 (.12) | 29 | 0.87 (.13) | -0.02 (1.01) | 80 |
| 3 | 0.50 | 0.37 (.19) | 27 | 0.28 (.13) | 30 | 0.44 (.27) | 6 | 0.33 (.18) | -0.19 (.36) | 63 |
| 4 | 0.67 | 0.00 (.00) | 25 | 0.00 (.00) | 8 | 0.00 ( -- ) | 1 | 0.00 (.00) | 0.00 (.00) | 34 |
| 5 | 0.83 | 0.00 (.00) | 12 | 0.00 (.00) | 2 | 0.00 (.00) | 0.00 (.00) | 14 | ||
| 6 | 1.00 | 0.00 (.00) | 3 | 0.00 (.00) | 0.00 (.00) | 3 | ||||
| 0.64 (.40) | -0.05 (.56) | 283 | ||||||||
| b | N = 20 | |||||||||
| 0 | 0.00 | 1.00 (.00) | 2 | 1.00 (.00) | 27 | 1.00 (.00) | 0.00 (.00) | 29 | ||
| 1 | 0.17 | 1.00 (.00) | 6 | 1.00 (.00) | 29 | 1.00 (.00) | 66 | 1.00 (.00) | 0.00 (.00) | 101 |
| 2 | 0.33 | 0.88 (.13) | 38 | 0.87 (.13) | 54 | 0.81 (.11) | 34 | 0.85 (.12) | -0.17 (.99) | 126 |
| 3 | 0.50 | 0.29 (.11) | 48 | 0.44 (.28) | 42 | 0.67 (.47) | 2 | 0.37 (.23) | -0.13 (.44) | 92 |
| 4 | 0.67 | 0.00 (.00) | 29 | 0.00 (.00) | 3 | 0.00 (.00) | 0.00 (.00) | 32 | ||
| 5 | 0.83 | 0.00 (.00) | 6 | 0.00 (.00) | 0.00 (.00) | 6 | ||||
| 6 | 1.00 | |||||||||
| 0.70 (.36) | -0.09 (.61) | 386 | ||||||||
Table B.1 shows the results for n = 4, N = 10 (a) and N = 20 (b) respectively. In column (1) we present the number of realized exchange relationships that can vary between 0 and the maximal possible number (see Table 5.1). In column (2) we present the corresponding density of the network. Columns (3) and (4), (5) and (6), and (7) and (8) show the average degree of segmentation and standard deviation within brackets and the number of cases (networks) on which the average is computed, for q = 0.20, q = 0.10, and q = 0.05, respectively. Column (9) gives the average and standard deviation of S3 over all values of q together. Column (10) presents the corresponding normalized segmentation index NS3 , and column (11) presents the number of cases on which the values in columns (10) and (11) are based.
2In Zeggelink (1998) such a potential explanation was given for the emergence of groups in the context of friendship relations, that is, within the larger scope of friendship networks.
3Kranton (1996) allows for the unlimited potential choice for new partners (cooperation) after an initially specified matching of partners. On the basis of certain assumptions, actors can always find a new partner if they terminate an existing relationship. Cooperation can however still be sustained if actors monotonically increase the level of cooperation within a relationship. With this strategy it is always better to continue in a current relationship than to 'cheat' and start again with a new partner. Her analyses suggest, but do not show right away, that when information is costly, establishing communities within which cooperation can be sustained must involve cost barriers to entry. Consequently a population can become segmented into different groups.
4Hence, the proportion of social strategies, the harshness of conditions (determining the probability of actors to get in distress), and the size of the initial population are the main factors that determine the viability of the social strategy.
5Boorman and Levitt (1980) make the implicit assumption that endogamous social units are already present in the initial stage of their model. The problem of explaining the emergence of a local concentration of sociality remains unsolved. A similar assumption exists in the work of Boyd and Richerson (1985) who start with the ethnic group as a basis. Other studies incorporate likewise assumptions (Axelrod 1984, Boyd and Richerson 1988 , Reeve 1998).
6Related to group living on the basis of reciprocal altruism is the so-called communal orientation of the group members. A communal orientation means a concern for each other's and one's own welfare. You benefit each other in response to need and in order to demonstrate concern. Receipt of a benefit does not create a specific debt or obligation to return a comparable benefit soon afterward. Neither does it alter the general obligation both of you have to be responsive to each other's needs (Mills and Clark 1982).
7 This is neither to say that such a situation is easy to define, nor that humans ever actually lived in these circumstances. However, if we say a socially unstructured population, it is important to be precise about what the absence of structure means. We mean that the only social relations assumed to exist initially are kinship relations. The elementary units in our model are basically conjugal or extended families. At the outset, these units have no mutual social relationships. For simplicity's sake, we call these elementary actors 'individuals' or 'actors', because they are the only acting units in our model. "Scratch" does not mean the complete absence of cooperation. An appropriate way to formulate the problem is to start with a population in which the individuals are organized in kinship groups and with kin-directed altruism concentrated exclusively within the units. This population could be interpreted as an abstraction of a Pleistocene social organization of hunters and gatherers, with all non-kinship-based-cooperation removed. The units then resemble so-called minimal bands that consist of 'several families of consanguine and/or affinal relatives who, at least during part of the year, share a common settlement and participate in a given range of cultural activities'. Then, the kind of cooperation to be explained is the tendency of a minimal band 'to participate in a larger social network in order to enhance its chance of biological and cultural survival', this larger network being called the maximal band (Wobst 1974).
8Whenever we refer to an individual by 'he', we also mean to refer to the female form.
9 Since it concerns actors with equal differences, this implies that this is the same actor for which the number of times support provided is highest.
10Since a social actor will never provide help to another actor twice in a row, without having been helped by that other actor in between, the difference number of times help given and received will either be equal to -1, 0, or 1 for every other actor.
11For reasons mentioned in the previous footnote, an asocial actor will never receive help from a social actor once he has already received help from that actor in a previous time period. However, an asocial actor does not have this knowledge. Would we assume that he had this knowledge, it would make more sense for an asocial actor to just distinguish other actors in those who have helped and those who have not.
12The choice of this value is certainly discussible (see Dawkins 1976)
13We do not take into account here that an actor will not provide help to the same actor twice in a row (in different periods) if that other actor has not provided help in return in between.
14We do not consider group size beyond G = 20 because we have simulation results only for initial population sizes up to 20.
15 Things would look different if we would allow for group growth, for instance as a result of 'birth-' and immigration' processes. That would be possible, if we would consider generations one after the other.
16For q = 0.2, this combines the results for costs of help being equal to c = 0.1, c = 0.05, and c = 0.025. For q = 0.1, this combines the results for c = 0.05, c = 0.025, and c = 0.0125. For q = 0.05, this combines the results for c = 0.025, c = 0.0125, and c = 0.00625. For every value of q, the total number of cases is 1650.
17This is therefore the general tendency, also for larger networks of social actors: Looking at a network of a certain size, it appeared more frequently for N = 20 than for N = 10. However, for N = 20 the percentages of networks with low density occur relatively more frequently than the networks with high density.
18 Other not reported results, related to the work in De Vos et al. (2000), show that segmentation increases to the extreme end once social actors apply the so-called commitment strategy.
19Actually, we would also have to take into account that reciprocity comes into play. We would need to know what the probability is to ask another actor, that is not in distress, for help, when we know that an actor asks those that have been helped by him before. This becomes too cumbersome. It would, among other things, mean taking into account that an actor's probability to get in distress increases in the period following the period he has helped another actor.
20If x = i, all actors in distress are successful and the whole term within braces. This probability definition is completely based on the lack of knowledge of all actors, and asks for a new definition in case more information would be available to the actors. This would for example imply higher probabilities for the same number of successes if only actors would be able to know which actors are in distress and which are not.
21Actors in distress that succeed in the first interval, and as a result get help, cannot provide help in this period. Only at the beginning of the next period they are defined to be no longer in distress.
AXELROD R and Hamilton W D (1981) The evolution of cooperation in biological systems. Science 211. pp. 1390-1396.
BAERVELDT C and Snijders T A B (1994) Influences on and from the segmentation of networks: hypotheses and tests. Social Networks. pp. 213-232.
BOORMAN S A and Levitt P R (1980) The genetics of altruism. New York: Academic Press.
BOYD R and Richerson P J (1985) Culture and the Evolutionary Process. Chicago: University of Chicago Press.
BOYD R and Richerson P J (1988) The evolution of reciprocity in sizeable groups. Journal of Theoretical Biology 132. pp. 337-356.
BREWER M B and Miller N (1996) Intergroup relations. Buckingham: Open University Press.
BREWER M B and Kramer R M (1986) Choice behavior in social dilemmas: effects of social identity, group size, and decision framing. Journal of Personality and Social Psychology 50. pp. 543-549.
BROWN J S, Sanderson M J and Michod R E (1982) Evolution of social behavior by reciprocation. Journal of Theoretical Biology 99. pp. 319-339.
CAMPBELL B (1979) Ecological factors and social organization in human evolution. In Bernstein I S and Smith E O (Eds.), Ecology and human origins: ecological influences on social organization. New York: Garland STPM Press.
COOPER B and Wallace C (1998) Evolution, partnerships and cooperation. Journal of Theoretical Biology 195. pp. 315-329.
DAWKINS R (1976) The Selfish Gene. Oxford: Oxford University Press
DE VOS H and Zeggelink E P H (1994) The emergence of reciprocal altruism and group-living: an object oriented simulation model of human social evolution. Social Science Information 33. pp. 493-517.
DE VOS H and Zeggelink E P H (1997) Reciprocal altruism in human social evolution: the viability of reciprocal altruism with a preference for 'old-helping-partners'. Evolution and Human Behavior 18. pp. 261-278.
DE VOS H, Smaniotto R and Elsas D A (2000) Reciprocal altruism under conditions of partner selection. Under review.
DUNBAR, R I M (1993) Coevolution of neocortical size, group size, and human language. Behavioral and Brain Sciences 16. pp. 681-694.
DUGATKIN L A and Wilson D S (1991) ROVER: A strategy for exploiting cooperators in patchy environments. The American Naturalist 138. pp. 687-701.
ERICKSON, B. (1988) "The relational basis of attitudes". In B. Wellman, and S. Berkowiz (Eds.) Social Structures: A network approach. Cambridge: Cambridge University Press.
FLACHE A. and Hegselmann R (1999) Altruism vs. self-interest in social support. Computer simulations of cooperation and partners election in social support networks. Advances in Group Processes 16. pp. 61-97.
FREEMAN L C (1992) The sociological concept of 'group': an empirical test of two models. American Journal of Sociology 98. pp. 152-166.
GALANTER M (1978) The 'relief-effect': A sociobiological model for neurotic distress and large- group therapy. American Journal of Psychiatry 135. pp. 588-591.
HOMANS, G. (1950) The human group. New York: Harcourt Brace.
KNAUFT B M (1991) Violence and sociality in human evolution. Current Anthropology 32. pp. 391-409
KRAMER R M, and Brewer M B (1984) Effects of group identity on resource use in a simulated commons dilemma. Journal of Personality and Social Psychology 46. pp. 1044-1057.
KRAMER R M, and Brewer M B (1986) Social group identity and the emergence of cooperation in resource conservation dilemmas. In Wilke H A M, Messick D M and Rutte G C (Eds.), Experimental social dilemmas. Frankfurt: Peter Lang.
KRANTON R E (1996) The formation of cooperative relationships. Journal of Law, Economics, and Organization 12. pp. 214-223.
KURLAND J A and Beckerman S J (1985) Optimal foraging and hominid evolution: Labor and reciprocity. American Anthropologist 87. pp. -93
MACY M W and Skvoretz J(1998) The evolution of trust and cooperation between strangers: a computational model. American Sociological Review 63. pp. 638-660.
MILLS J and Clark M S (1982) Exchange and communal relationships. In Wheeler L (Ed.), Review of personality and social psychology, vol. 3. Beverly Hills: Sage.
MULLEN, B. and G. Goethals (1987) Theories of group behavior. New York: Springer-Verlag.
NETTLE D and Dunbar R I (1997) Social markers and the evolution of reciprocal exchange. Current Anthropology 38. pp. 93-99.
NOWAK M A and May R M (1992) Evolutionary games and spatial chaos. Nature 359. pp. 826-829.
NOWAK M A, Bonhoefer S, and May R M (1994a) Spatial games and the maintenance of cooperation. Proceedings of the National Academy of Sciences 91. pp. 4877-4881.
NOWAK M A, Bonhoefer S and May R M (1994b) More spatial games. International Journal of Bifurcation Chaos 4. pp. 33-56.
REEVE H R (1998) Acting for the good of others: kinship and reciprocity with some new twists. In Crawford C C and Krebs D L (Eds.) Handbook of Evolutionary Psychology. Ideas, Issues, and Applications. Mahwah, N.J.: Erlbaum.
ROOK, K.S. (1987) "Social support versus companionship: effects on life stress, loneliness, and evaluations by others". Journal of Personality and Social Psychology 52: 1132-1147.
SHAW M. (1981) Group dynamics: the psychology of small group behavior. New York: McGraw-Hill.
SCHUESSLER R. (1989) Exit threats and cooperation under anonymity. Journal of conflict resolution 33. pp. 728-749.
STANLEY E A, Ashlock D and Smucker M D (1995) Iterated Prisoner's Dilemma with choice and refusal of partners: evolutionary results. Lecture Notes in Computer Science 929. pp. 495-502.
STEVENS, A. and J. Price (1997) Evolutionary Psychiatry. London: Routledge.
TAJFEL, H. and J. Turner (1986) "The social identity theory of intergroup-behavior". In S. Worchel and W. Austin (Eds.) Psychology of intergroup relations. Chicago: Nelson-Hall Publishers.
TRINKAUS E (1989) The upper Pleistocene transition. In Trinkaus E (Ed.) The emergence of modern humans: Biocultural adaptation in the later Pleistocene. Cambridge: Cambridge University Press.
TRIVERS R (1971) The evolution of reciprocal altruism. Quarterly Review of Biology 46. pp. 35-56.
VANBERG V J and Congleton R D (1992) Rationality, morality, and exit. American political science review 86. pp. 418-431.
WILSON D S and Dugatkin L A (1997) Group selection and assortative interactions. The American Naturalist 149. pp. 336-351.
WINTERHALDER B. (1986) Diet choice, risk, and food sharing in a stochastic environment. Journal of Anthropological Archaeology 5. pp. 369-392.
WOBST H M. (1974) Boundary conditions for Paleolithic social systems: a simulation approach. American Antiquity 39. pp. 147-178.
YAMAGISHI T, Hayashi N and Jin N (1994) Prisoner's dilemma networks: selection strategy versus action strategy. In Schulz U, Albers W and Mueller U (Eds.) Social dilemmas and cooperation. New York: Springer Verlag.
ZEGGELINK E P H, Stokman F N, and Van De Bunt G G (1996) The emergence of groups in the evolution of friendship networks. Journal of Mathematical Sociology 21. pp. 29-55.
ZEGGELINK, E.P.H. (1998) "Group formation in friendship networks". In P. Doreian and T. Fararo (Eds.) The problem of solidarity: theories and models. Amsterdam: Gordon and Breach Publishers.
ZEGGELINK E P H. (2000) The degree of segmentation reconsidered. Paper to be presented at the Fifth International Conference on Social Science Methodology in Cologne, Germany, October 3-6, 2000.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999