Gérard Ballot and Erol Taymaz (1999)
Journal of Artificial Societies and Social Simulation vol. 2, no. 2, <https://www.jasss.org/2/2/3.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 29-Dec-98 Accepted: 8-Apr-99 Published: 14-Apr-99
![]()
 Abstract
Abstract| Table 1: Decision types and determinants of the four actions | ||||
| Simple | Informed | Optimiser | Follower | |
| Actions | ||||
| Change in planned output | Past change : + Past expected errors : - Learning rate : + | Same as simple type | Short run profit max problem | Same as simple type |
| Desired Investment in R&D | A percentage of sales revenue | A function of : general human capital stock : + radical R&D : + learning rate : + sales revenue : + | Same as informed type but modified with rate of return to R&D/interest rate ratio | Imitate the average of the top 50 per cent of firms |
| Desired Investment in training | Same as above | A function of : human capital stock : + separation rate : - best practice/average practice output : + sales revenue : + | Rate of return to training/interest rate | Same as above |
| Desired Investment in physical capital | Same as above | A function of : - capacity utilisation rate : + - fixed capital stock : + - rate of return minus interest rate : + | Same as informed type | Same as above |
RD(i) = a(i1)* S(i)where RD(i), TR(i), and PK(i) are ith firms' desired expenditures on total R&D, total training, and fixed assets, and Si is its sales revenue. The firm learns which values of these parameters a(i1), a(i2), and a(i3) improve profitability and market share through the classifier system.TR(i) = a(i2)* S(i)
PK(i) = a(i3) * S(i)
RD(i) = e(i)*S(i)* RDBwhere RDB is the average share of R&D expenditures in sales of the successful firms, TRB is the average share of training expenditures in sales of those firms, and PKB is the average share of their fixed assets expenditures.TR(i) = e(i2)*S(i)*TRB
PK(i) = e(i3)*S(i)*PKB
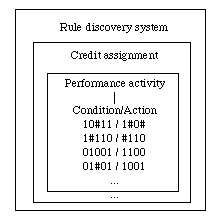
|
| Figure 1: The classifier system |
BID(j) = ST(j) /(1+GEN(j))where ST(j) is the strength of the rule j, and where GEN(j) is equal to the number of # elements in the condition part of the jth rule. In our example, a 01#01 observation vector matches rules 3 and 4. Rules 3 and 4 lead to contradictory actions, since rule 3 suggests to increase training, while rule 4 suggests to decrease it. The rule with the highest bid will be selected.
INT(k) = INT(k-1) * (1 + P1*ACT)/(1 + P2*abs(lnINT(k-1)))where INT(k) is the intensity variable for the application of the kth rule, and K(0) = 1. P1 and P2 are parameters (with values .5 and 5 respectively in the present sets of experiments). ACT is the action (1 for increase, -1 for decrease, 0 for no change), and abs (.) the absolute function. For instance, if two rules suggest to increase R&D, INT(k) = 1.5, so that the parameters b(i1) and b(i2) are increased by 50 per cent by applying the first rule. One sees that there are decreasing returns in INT. All parameters are changed in the same way except ci1, which relates the training expenditures to the rate of separation, and is assumed fixed, to keep the effects of changes proportional for all expenditures.
ST(j,T) = ST(j,T-1) + r*PST*PER(T)*(APP(j,T-1) + (1-r)*APP(j,T-2) + (1-r)*(1-r)*APP(j,T-3) + (1-r)*(1-r)*(1-r)*APP(j,T-4) + ... )where PER(T) is the performance of the firm at time T (1 if both criteria are satisfied, -1 if none of them is satisfied, 0 if one of them is satisfied). APP(j,t) takes the value 1 if the rule j has been applied in quarter t, and 0 if it has not been applied. PST and r are parameters (.5 and .1 respectively), r being a discounting factor. For example, if the rule was applied 1 and 2 and 4 quarters ago, then:
ST(j,T) = ST(j,T-1) + r*PST*PER(T)*((1-r) + (1-r)*(1-r))
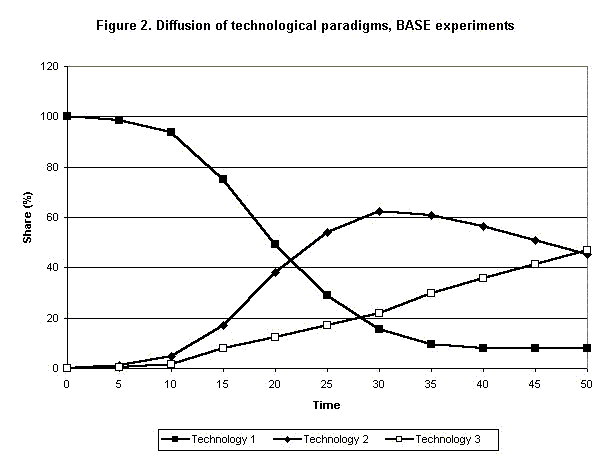
|
| Table 2: Macroeconomic performance | ||||
| BASE | NOLEARN | NODIV | NOENTRY | |
| G.N.P (BILLIONS OF SKR) | 3628 | 3219* | 2913* | 3407* |
| TECHNOLOGY LEVEL | 2.38 | 1.83* | 2.30 | 2.49* |
| AVERAGE RATE OF INCREASE OF PRODUCTIVITY | 8.60 | 7.50* | 7.17* | 8.23 |
| * Significantly different from BASE at the 5 per cent level. | ||||
| Table 3: Entry and exit rates and the Herfindahl index of concentration | ||||
| BASE | NOLEARN | NODIV | NOENTRY | |
| ENTRANTS | 111.8 | 114.1 | 120.6* | 0* |
| EXITS | 105.7 | 108.1 | 99.7* | 100.3* |
| NUMBER OF FIRMS | 231 | 231 | 246* | 125* |
| HERFINDAHL INDEX | ||||
| SECTOR 1 : RAW MATERIAL | 0.102 | 0.129 | 0.170 | 0.316* |
| SECTOR 2 : INTERMEDIATE GOODS | 0.134 | 0.209 | 0.168 | 0.205 |
| SECTOR 3 : CAPITAL GOODS | 0.097 | 0.166 | 0.226* | 0.232* |
| SECTOR 4 : CONSUMER GOODS | 0.397 | 0.417 | 0.397 | 0.639* |
| ALL SECTORS : | 0.183 | 0.231 | 0.241* | 0.349* |
| * Significantly different from BASE at the 5 per cent level. | ||||
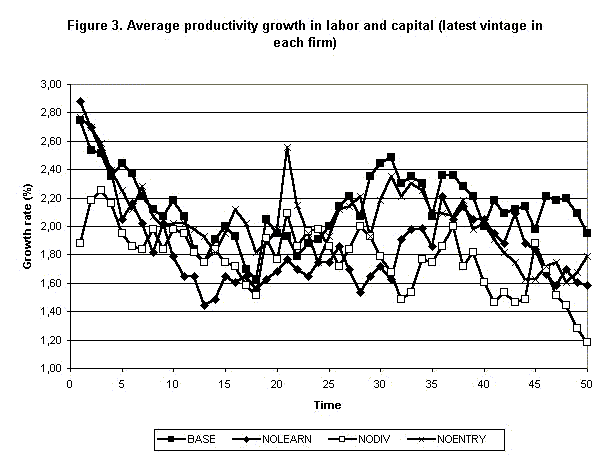
|
| Table 4: Distribution of firms by decision type (end of simulation) | ||||
| SIMPLE | OPTIMIZER | INFORMED BEHAVIOR | FOLLOWER | |
| BASE | 26 | 24 | 25 | 24* |
| NOLEARN | 22 | 26* | 26* | 26* |
| NODIV | - | - | 100 | - |
| NOENTRY | 25.5 | 27* | 25 | 26 |
| * Significantly different from BASE at the 5 per cent level. | ||||
| Table 5: Market shares by decision type | ||||
| BASE | NOLEARN | NODIV | NOENTRY | |
| SIMPLE | 29.1 | 48.3* | -- | 28.1* |
| INFORMED BEHAVIOR | 24.7 | 16.1 | 100 | 19.8 |
| OPTIMIZER | 24.9 | 14.9 | -- | 20.7 |
| FOLLOWER | 21.2 | 20.0 | -- | 31.3* |
| * Significantly different from BASE at the 5 per cent level. | ||||
| Table 6: Rates of return by decision type | ||||
| BASE | NOLEARN | NODIV | NOENTRY | |
| SIMPLE | 18.9 | 17.3 | -- | 21.2 |
| INFORMED BEHAVIOR | 18.4 | 17.6 | -- | 21.8 |
| OPTIMIZER | 18.9 | 18.4 | -- | 22.3 |
| FOLLOWER | 17.9 | 14.5 | -- | 21.2 |
| Table 7: Rules' strength values at the end of simulation | ||||
| BASE | NOLEARN | NODIV | NOENTRY | |
| MAXIMUM STRENGTH VALUE PER FIRM | 0.729 | 0.108 | 0.104 | 1 |
| MEAN STRENGTH VALUE PER FIRM (ON 32 RULES) | 0.758 | 0.240 | 0.237 | 0.826 |
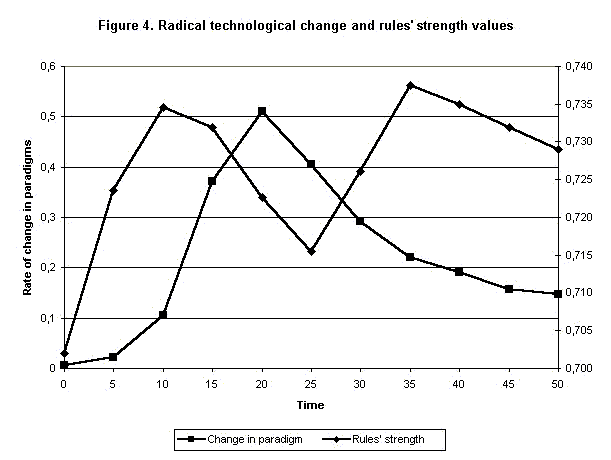
|
 Appendix
Appendix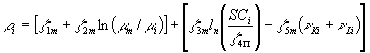 [1]
[1]
where m m is the average paradigm level of sector m and m i the paradigm level of the firm, SCi the number of past successes of the firm in radical innovations, n K the rate of improvement of productivity (or learning rate) of capital, and n l the learning rate for labour.z 1m, z 2m, z 3m, z 5m, are sector specific parameters (m = 1, ...4). z 4p is paradigm specific (p = 1,2,3).
RDi = (bi1*GHCi*Li) + (bi2*r pi*w i*Si) [2]
where GHCi is the general human capital stock, r pi the past share of radical R&D in total R&D, and w i the increase in productivity.
Desired total investment in training:
TRi = (1-ci1*s)*(QTOPFRi/QTOPi)*(ci2*Si) +( ci3*Li*(GHCi + SHCi)) [3]
where s is the quit rate, GHCi and SHCi the general and specific human capital stock.
Desired investment in fixed assets:
IKi = (Qi/QMAXi)* Ki *[di1+di2*(QDPK+ RRi -RIFi)] [4]
where QDPK corresponds to the capital gains, RRi to the rate of return, and RIFi to the borrowing rate of interest.
 Acknowledgments
AcknowledgmentsEarlier versions of the paper were presented at the conference "Economic Evolution, Learning and Complexity" (Augsburg, Germany, May 22-25, 1997) and the SIMSOC Conference (Cortona, Italy, September 22-25, 1998).
A grant from the French Commissariat Général du Plan (subsidy 25.95) for research on firm's human capital is gratefully acknowledged. Erol Taymaz thanks the University Paris II for the invitation as a Guest Professor, during which part of the research was done.
 Notes
Notes2See Patel and Pavitt (1991) for some evidence.
3See Gilbert and Doran (1994) for concepts and simulation models of emergence in social sciences.
4Chiaramonte and Dosi (1992) supply an evolutionary model which shows the importance of diversity.
5Akerlof and Yellen (1985) have shown that small deviations from rationality may matter little for firms, but a lot for aggregate variables.
6Sargent's (1993) survey testifies this.
7A set of manuals give a full description of MOSES before the introduction of human capital and technological change: Albrecht et al. (1989; 1992), Taymaz (1991). A synthesis is given by Eliasson (1991). The model with a synthetic database is available for all researchers.
8See Dosi and Marengo (1994) for an excellent synthesis.
9See Reinganum (1989) for the first approach, which focuses on the determination of R&D expenditures in the patent race. Silverberg, Dosi and Orsenigo (1988) is an example of the second approach.
10Eliasson (1994) provides a very detailed and thought provoking analysis of human capital issues with the same intellectual focus, i.e. economic competence of firms and aggregate growth.
11However they may imitate fast and reap some rent.
12We prefer the term "technological paradigm" coined by Dosi (1982) for the sake of linguistic elegance.
13This assumption does not reduce generality. It corresponds to the use of a binary alphabet, which is very flexible.
14See Goldberg (1989) for an excellent introduction to genetic algorithms.
15For a prior modelling enterprise, dealing only with the R&D expenditures as a learning process, see Silverberg and Verspagen (1994). Another model, developed by Merlateau and Langrognet (1994), introduces learning of the best proportions of workers in the R&D department, and of trained workers in production, with the tool of neural networks.
16Booker, Goldberg and Holland (1990) provide a thorough introduction.
17We borrow the image from Booker, Goldberg and Holland (1990) , p. 255.
18Ballot and Taymaz (1998) provide a detailed analysis, in a version with fixed rules and parameters of allocation.
19For a recent survey of issues, see Cohendet, Llerena and Marengo (1994).
ALBRECHT JW et al. (1989) MOSES Code.Stockholm:IUI.
ALBRECHT JW et al. (1992) MOSES Database. Stockholm: IUI.
ARROW K (1962) The economic implications of learning-by-doing. Review of Economic Studies, 29(2), pp 155-173.
ARTHUR WB (1988) Competing technologies: an overview. In Dosi G et al. (eds) Technical Change and Economic Theory, Pinter: London.
BALLOT G (1994) Continuing education and Schumpeterian competition. Elements for a theoretical framework. In Asplund R (ed.), Human Capital Creation in an Economic Perspective, Berlin: Physica Verlag/Springer-Verlag.
BALLOT G and TAYMAZ E (1993) Firms sponsored training and performance. A comparison between France and Sweden based on firms data. 5th EALE Conference, Maastricht Netherlands, Oct.1-3 (ERMES Working Paper n. 93-09).
BALLOT G and TAYMAZ E (1994) Training, learning and innovation. A micro-to-macro model of evolutionary growth. The International J.A.Schumpeter Society Conference on Economic Dynamism: Analysis and Policy, Münster, Germany, August 17-20.
BALLOT G and TAYMAZ E (1996) Firm sponsored training, technical change and aggregate performance in a micro-macro model. In Harding A (ed.), Microsimulation and Public Policy ,Amsterdam: North Holland.
BALLOT G and TAYMAZ E (1997) The dynamics of firms in a micro-to-macro model with training, learning, and innovation. Journal of Evolutionary Economics, 7, 435-457.
BALLOT G and TAYMAZ E (1998) Human Capital, Technological Lock-in and Evolutionary Dynamics. In Eliasson G and Green C (eds.), Microfoundations of Economic Growth: A Schumpeterian Perspective, Ann Arbor: The University of Michigan Press, 301-330.
BECKER GS (1964) Human Capital. New York: NBER.
BOOKER LB, GOLDBERG DE, and HOLLAND JH (1990) Classifier systems and genetic algorithms. In Carbonnel J (ed), Machine Learning: Paradigms and Methods, Cambridge: MIT Press.
CHIARAMONTE F and DOSI G (1992), The microfoundations of competitiveness and their macroeconomic implications. In Foray D and Freeman C (eds.), Technology and the Wealth of Nations. London: Francis Pinter.
CHIARAMONTE F, DOSI G, and ORSENIGO L (1993) Innovative learning and institutions in the process of development: on the microfoundation of growth regimes. In Thomson R (ed.), Learning and Technological Change, New York: St.Martin's Press.
COHEN WM and LEVINTHAL DA (1990) Absorptive capacity: a new perspective on learning and innovation. Administrative Science Quaterly, 3, 128-152.
COHENDET P, LLERENA P, and MARENGO L (1994) Learning and organisational structure in evolutionary models of the firm, Eunetic Conference, Strasbourg, France, October 6-8.
CYERT RM and MARCH JG (1963) A Behavioural Theory of the Firm, Cambridge: Blackwell.
DOSI G (1982) Technological paradigms and technological trajectories. Research Policy, II (3), 147-162
DOSI G and MARENGO L (1994) Some elements of evolutionary theory of organisational competences. In England RW (ed), Evolutionary Concepts in Contemporary Economics. Ann Arbor: The University of Michigan Press.
DOSI G and ORSENIGO L (1994) Macrodynamics and microfoundations: an evolutionary perspective. In Granstrand O (ed), Economics of Technology, Amsterdam: North Holland.
ELIASSON G (1977) Competition and market processes in a simulation model of the Swedish economy. American Economic Review, 67, 277-281.
ELIASSON G (1985), The Firm and Financial Markets in the Swedish Micro-to-Macro Model. Stockholm: IUI and Almqvist and Wiksell International.
ELIASSON G (1991) Modelling the experimentally organised economy. Journal of Economic Behaviour and Organization,16, 163-182.
ELIASSON G (1994) General purpose technologies, industrial competence and economic growth, working paper, Department of Industrial Economics and Management Working Paper, The Royal Institute of Technology, Stockholm.
FAGERBERG J (1994) Technology and international differences in growth rates. Journal of Economic Literature, XXXII, 1147-1175.
FREEMAN C and PEREZ C (1988) Structural crises of adjustment: business cycles and investment behaviour. In Dosi G et al. (eds), Technical Change and Economic Theory, London: Pinter, 38-66.
GILBERT N and DORAN J (eds) (1994) Simulating Societies, London: UCL Press.
GOLDBERG DE (1989) Genetic Algorithms in Search, Optimisation and Machine Learning, Reading, Mass: Addison-Wesley.
HOLLAND JH (1976) Adaptation. In.Rosen R and Snell FM (eds), Progress in Theoretical Biology IV, New York: Academic Press, 263-293.
HOLLAND JH and MILLER JH (1991) Artificial adaptive agents in economic theory. American Economic Review, 81(2), 365-370.
MERLATEAU M-P and LANGROGNET E (1994) An evolutionary model with human capital, Eunetic Conference, Strasbourg, France, October 3-6 (ERMES discussion paper 94-07).
MUELLER DC (1990) The Dynamics of Company Profits. An International Comparison. Cambridge: Cambridge University Press.
NELSON RR (1994) The coevolution of technologies and institutions. In England RW (ed.), Evolutionary Concepts in Contemporary Economics, Ann Arbor: The University of Michigan Press.
PATEL P and PAVITT K (1991) Large firms in Western Europe's technological competitiveness. In Mattson LG and Stymme B (eds.), Corporate and Industry Strategies for Europe.Amsterdam: Elsevier.
REINGANUM J (1989) The timing of innovation: research, development and diffusion. In Schmalensee R and Willig R (eds), Handbook of Industrial Organisation, vol 1, Amsterdam: North Holland.
SARGENT TJ (1993) Bounded Rationality in Macroeconomics, Oxford: Clarendon Press.
SCHUMPETER J (1934) The Theory of Economic Development, Cambridge, Mass.: Harvard University Press.
SILVERBERG G, DOSI G, and ORSENIGO L(1988) Innovation, diversity and diffusion: a self-organisation model. The Economic Journal, 98, 212-221.
SILVERBERG G and VERSPAGEN B (1994) Collective learning, innovation and growth in a boundedly rational, evolutionary world. Journal of Evolutionary Economics, 4 (3), 207-226.
SIMON HA (1976) From substantive to procedural rationality. In Latrès SJ (ed), Method and Appraisal in Economics, Cambridge: Cambridge University Press.
SOMIT A and PETERSON SA (eds) (1989) The Dynamics of Evolution. The Punctuated Equilibrium Debate in the Natural and Social Sciences. Ithaca: Cornell University Press.
TAYMAZ E (1991) MOSES on PC: Manual, Initialization and Calibration. Stockholm: IUI.
VON HIPPEL E (1988) The Sources of Innovation, New York: Oxford University Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999