Marco Janssen and Wander Jager (1999)
Journal of Artificial Societies and Social Simulation vol. 2, no. 2, <https://www.jasss.org/2/2/2.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 2-Feb-99 Accepted: 10-Mar-99 Published: 14-Apr-99
![]()
 Abstract
Abstract
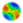
|
| Figure 1: Share of product 1 for 3 possible runs of the very simple model |
(1) Si = Shi*D
The share of the demand is adjusted by changed in indicated shares (IndShi):
(2) dShi/dt = (IndSh-Sh)/ta
This indicated share is determined by a multinomial logit function of the prices of the products. This logit function weights the relative prices (Pi) where parameter mu indicates the sensitivity of the consumers to price differences.
(3) IndShi = EXP(-mu*Pi)/(EXP(-mu*P1)+EXP(-mu*P2))
Prices depend on fixed and variable costs, and a learning factor:
(4) Pi = LFi*(FCi + Si*VCi)/Si
The learning factor (LF) decreases by cumulative production of the product according to the principle of learning-by-doing (Arrow, 1962). The more a product has been produces, the lower the cost price per unit. The parameter gamma determines the cost reduction per doubling of cumulative production.
(5) LFi = (CLi / CLI-in)-log10(gamma)/log10(2)
(6) dCLi/dt= Si
(1'a) S1 = MIN(Sh1*D+ N(0,sigma),D)
(1'b) S2 = D - S1
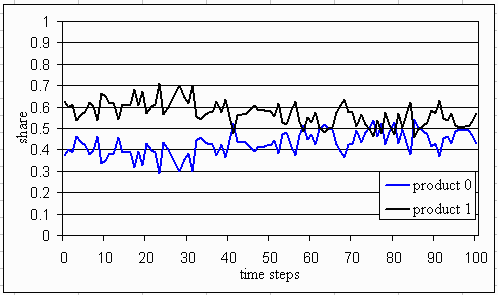
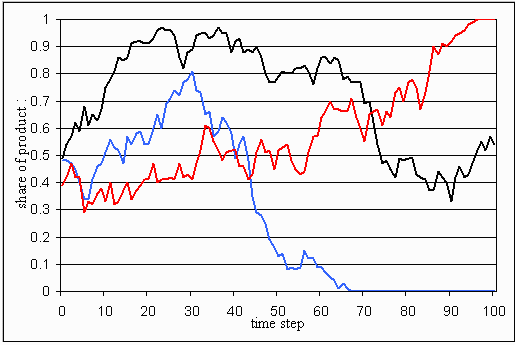
|
|
| Figure 2. Two possible developments of the market given two identical products (ta=2, gamma=0.9, sigma=0.5, FC=10 and VC=10). A lower sensitivity for the demand for price differences (mu=0.5) was used in the upper figure than in the lower figure (mu=0.65). |

|
| Figure 3: The Moore neighborhood template. The red cells are neighbours of the cell in the middle of the lattice. |
|
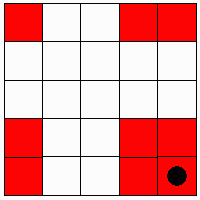
| Figure 4: The red cells are the neighbors of the cell in the left lower corner of the lattice. |
|
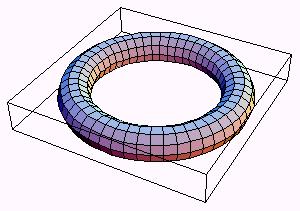
| Figure 5: A torus, a 2-dimensional cellular automatum with the edges pasted (Hegselman and Flache, 1998). |
|
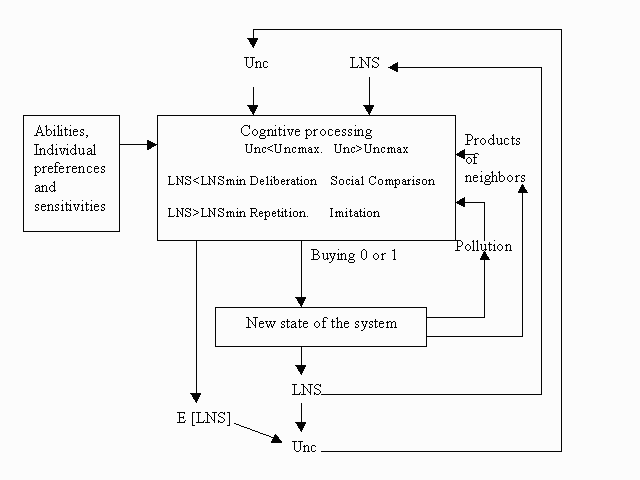
| Figure 6: Schematic overview of the behavioural processes of the agents in relation to changes in their environment. |
LNS1 = 1-SxNij/8 if xij=0 else LNS1 = SxNij/8
LNS2 = b 0ij if xij=0 else LNS2 = b1ij
LNS3 = B/P0 if xij=0 else LNS3= B/P1
C=C-1*(1-m)+l0*#(xij=0) + l1 *(#xij =1)
Individual sensitivity to pollution (a ij) determines the individual level of satisfaction for the need subsistence and is related to the concentration level.
LNS4 = 1-exp(- aij/C)
LNSij = LNS1gamma1ij * LNS2gamma2ij LNS3gamma3ij * LNS41-gamma1ij-gamma2ij-gamma3ij
In fact, the way the different needs are implemented cause four different feedbacks: (1) the need for identity related to the local (neighbourhood) characteristics, (2) the need for personal taste is related to individual preferences, (3) the need for leisure related individual abilities to macro information (product prices), and (4) the subsistence need may lead to a product related feedback, while pollution is caused by consumption of specific products.
Uncij=S k abs(LNSkij -LNS-1kij)
Max (LNS(xij=0), LNS(xij=1))
LNS = LNS1gamma1ij * LNS2gamma2ij LNS3gamma3ij * LNS41-gamma1ij-gamma2ij-gamma3ij
LNS1 = 1-(S xNij)/8 if xij=0 else LNS1 = (SxNij)/8
LNS2 = b 0ij if xij=0 else LNS2 = b1ij
LNS3 = B/P0 if xij=0 else LNS3= B/P1
LNS4 = 1-exp(- aij/ (C-1*(1-m)+l 0)) if xij=0 else LNS4 = 1-exp(- aij/ (C-1*(1-m)+l1))
xij = 0 if
#[(xNij =0) and
(Bij * (1-Btol) £
Bneighbours £
Bij * (1+Btol))]
>
#[(xNij =1) and
(Bij * (1-Btol) £
Bneighbours £
Bij * (1+Btol)) ]
else xij = 1.
xij = x-1ij
xij = 0 if #(xNij=0) > #(xNij=1) else xij = 1.

|

|

|
| Figure 7: Spatial pattern in the lattice of consumption of product 0 (red) and 1 (blue), for 3 points in time (t=0, t=10 and t=100). |
|
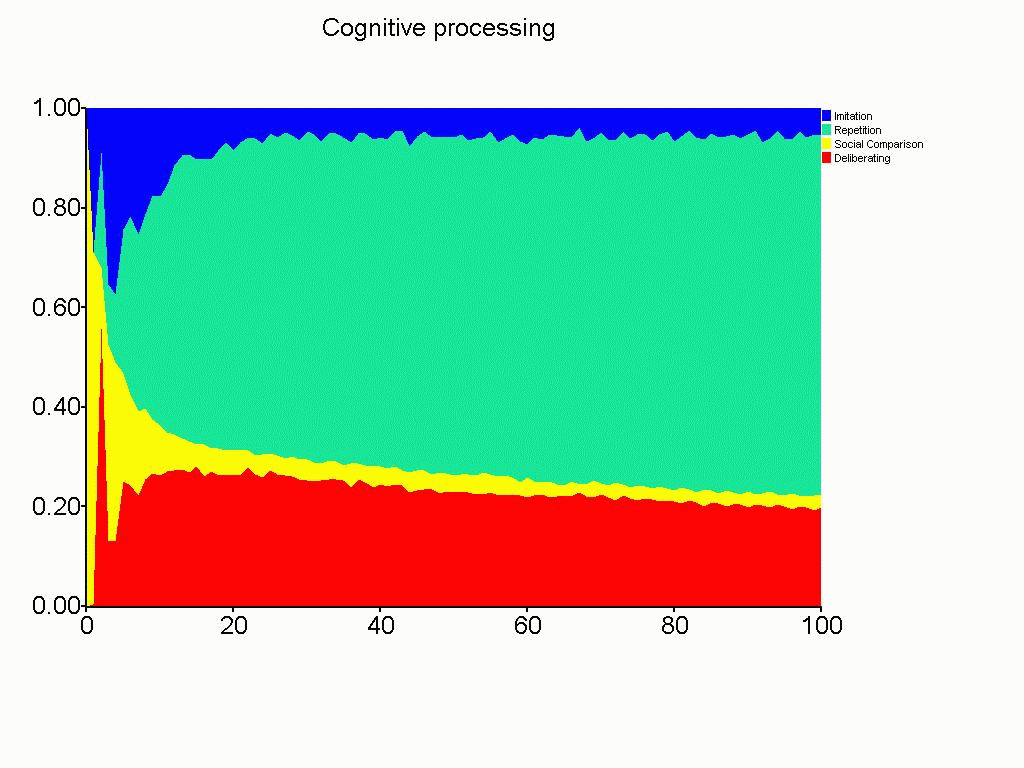
| Figure 8: Types of cognitive processes for the population of 900 consumats (red = delibertaing; yellow = social comparison; green = repetition; blue = imitation) |
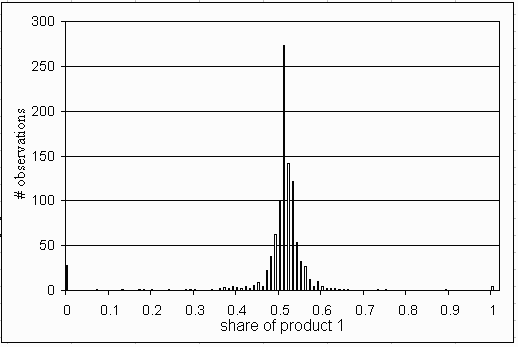
|
| Figure 9: Distribution of share of product 1 in time step 100. If this share is equal to 0 or 1 a macro-level lock-in has occurred. |
| Table 1: Statistics for the experiment of 1000 model runs: the average values of the model parameters and the standard deviation (in brackets). | ||
| General | Locked in | |
|---|---|---|
| Gamma1 | 0.251 (0.142) | 0.290 (0.147) |
| Gamma2 | 0.253 (0.142) | 0.020 (0.018) |
| Gamma3 | 0.250 (0.146) | 0.424 (0.164) |
| Gamma4 | 0.245 (0.141) | 0.266 (0.166) |
| LNSMIN | 0.499 (0.291) | 0.594 (0.272) |
| UncMAX | 0.493 (0.291) | 0.680 (0.214) |
| Btol | 0.499 (0.285) | 0.434 (0.241) |
| # | 1000 | 33 |
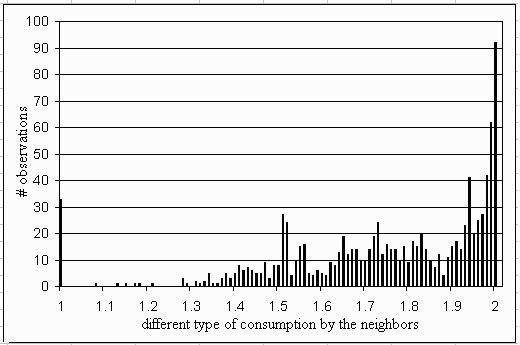
|
| Figure 10: Distribution of the average different types of products consumed by the neighbors in time step 100. If this average is 1, a macro-level lock-in has occurred. If this average is 2, the consumption is randomly distributed over the lattice. A low average suggests spatial patterns. |
| Table 2: Statistics based on the results of 1000 model runs (t-values are in brackets) | |
| R2 | 0.489 |
| c | 1.789 (53.15) |
| gamma1 | -0.538 (-11.48) |
| gamma2 | 0.685 (14.58) |
| gamma3 | -0.196 (-4.25) |
| LNSMIN | 0.159 (8.54) |
| UncMAX | -0.237 (-12.78) |
| Btol | 0.004 (0.21) |
| # | 1000 |
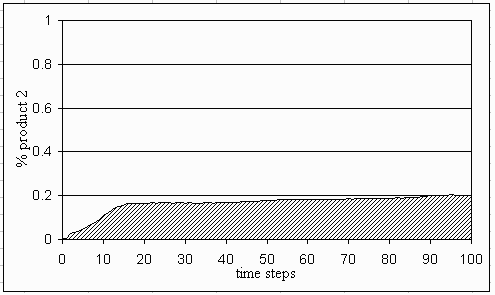
|
| Figure 11: The average share of product 2 for a whole range of time steps |
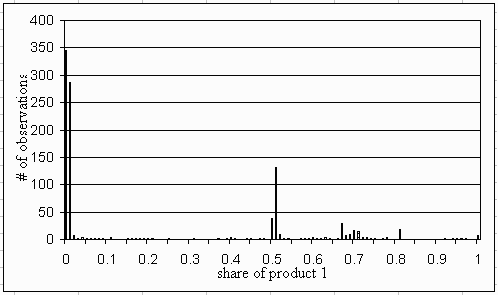
|
| Figure 12: Distribution of share of product 1 in time step 100. If this share is equal to 0 or 1 a macro-level lock-in has occurred |
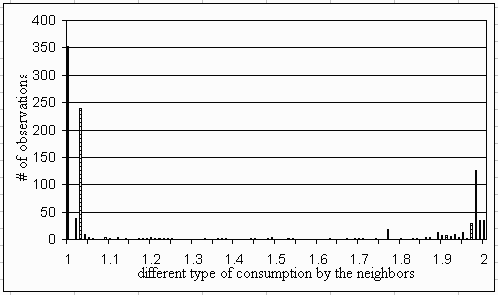
|
| Figure 13: Distribution of the average different types of products consumed by the neighbors in time step 100. If this average is 1, a macro-level lock-in has occurred. If this average is 2, the consumption is randomly distributed over the lattice. A low average suggests spatial patterns |
AJZEN, I. (1988). Attitudes, Personality, and Behaviour. Open University Press, Milton Keynes, England.
AJZEN, I. (1991). The theory of planned behavior. Organizational Behavior and Human Decision Processes, 50, 179-211.
AJZEN, I. and Madden, T.J. (1985). Prediction of Goal-Directed Behaviour: Attitudes, Intentions, and Perceived Behavioral Control. Journal of Experimental Social Psychology, Vol. 22, 453-474.
ARROW, K.J. (1962). The Economic Implications of Learning-by-doing, Review of Economic Studies, 29,155-73.
ARTHUR, W.B. (1989), Competing technologies, increasing returns, and lock-in by historical events, The Economic Journal, Vol. 99, 116-131.
BANDURA, A. (1977). Social learning theory. Englewood Cliffs, New Jersey: Prentice Hall.
BANDURA, A. (1986). Social Foundations of Thought and Action: A Social Cognitive Theory. Englewood Cliffs, NJ: Prentice Hall.
BANERJEE, A.V. (1992), A simple model of herd behavior, The Quarterly Journal of Economics, Vol. 152, no. 3, 797-817.
BIKHCHANDANI, S., D. Hirshleifer and I. Welch (1992), A Theory of fads, fashion, custom, and cultural change as informational cascades, Journal of Political Economy, vol. 100, no. 5, 992-1026.
CIALDINI, R.B., Kallgren, C.A., and Reno, R.R. (1991). A focus theory of normative conduct: a theoretical refinement and reevaluation of the role of norms in human behavior. In: L. Berkowitz (Ed.). Advances in Experimental Social Psychology, 24, pp. 201-234.
COOK, S.W and Berrenberg, J.L. (1981). Approaches to encouraging conservation behavior: A review and conceptual framework. Journal of Social Issues, 37(2), 73-107.
DAVID, P.A. (1985), Clio and the Economics of QWERTY, AEA Papers and proceedings, Vol. 75, no. 2, 332-337.
DE YOUNG, R., (1993). Changing behaviour and making it stick: The conceptualisation and management of conservation behaviour. Environment and Behaviour, Vol 25 (4). pp. 485-505.
FAUCHEUX, S., and Moscovici, C., (1972). Social influence, conformity, bias and the study of active minorities. In: L. Berkowitz (Ed.). Advances in experimental social psychology. Vol 6 (pp. 149-202).
FESTINGER, L. (1954). A theory of social comparision processes. Human Relations, 7, 117-140.
FISHBEIN, M. and Ajzen, I. (1975). Belief, Attitude, Intention, and Behaviour: An Introduction to Theory and Research. Reading, MA, USA: Addison-Wesley.
GRANOVETTER, M. and R. Soong (1986). Threshold Models of Interpersonal Effects in Consumer Demand, Journal of Economic Behaviour and Organization, 7, 83-99.
HEGSELMANN, R. and A. Flache (1998) Understanding Complex Social Dynamics: A Plea For Cellular Automata Based Modelling, Journal of Artificial Societies and Social Simulation vol. 1, no. 3,<https://www.jasss.org/1/3/1.html>
JAGER, W., Van Asselt, M.B.A., Rotmans, J., Vlek, C.A.J. and Costerman Boodt, P. (1997). Consumer Behaviour: A Modelling Perspective in the Context of Integrated Assessment of Global Change, Globo Report Series No. 17, RIVM, Bilthoven, the Netherlands.
JAGER, W., Janssen, M.A. and C.A.J. Vlek (1999). Consumats in a commons dilemma: Testing the behavioural rules of simulated consumers. COV report no. 99-01. Groningen: Centre for Environment and Traffic Psychology, University of Groningen. http://www.ppsw.rug.nl/cov/staff/jager/simpaper.pdf
JANIS, I. L. and Mann, L. (1977). Decision making; a psychological study of conflict, choice and commitment. New York/London: The Free Press.
KIRMAN, A. (1993), Ants Rationality, and Recruitment, The Quarterly Journal of Economics, February 1993, 137-156.
LEIBENSTEIN, H. (1976), Beyond economic man: A new foundation for microeconomics, Harvard University Press, Cambridge, MA.
LIEBOWITZ, S.J. and S.E. Margolis (1994), Network Externality: An Uncommon Tradegy, Journal of Economic Perspectives, 8 (2), Spring.
LIEBOWITZ, S.J. and S.E. Margolis (1995), Are Network Externalities a New Source of Market Failure?, Research in Law and Economics, 17, pp. 1-22.
MASLOW, A.H. (1954). Motivation and Personality. New York, USA: Harper and Row.
MASTERS, J.C., and Smith, W.P. (Eds.). (1987). Social comparison, social justice and relative deprivation: theoretical and policy perspectives. Volume 4. Hillsdale (N.J.): Erlbaum.
MAX-NEEF, M., (1992). Development and human needs. In: P. Ekins and M. Max-Neef (Eds.): Real-life economics: Understanding wealth creation. London, New York: Routledge.
ÖLANDER, F., and Thøgerson, J. (1994). Understanding consumer behaviour as a prerequisite for environmental protection. Keynote address presented at the 23rd International Congress of Applied Psychology. Aarhus (Denmark): Aarhus School of Business.
OPSCHOOR, J.B. (1989). Na ons geen zondvloed; voorwaarden voor een duurzaam milieugebruik (After us no deluge; conditions for a sustainable use of the environment). Kampen: Kok/Agora. (in Dutch)
PAVLOV, I.P. (1927). Conditioned reflexes. New York: Oxford University Press.
SHETH, J.N., and Frazier, G.L. (1982). A model of strategy mix choice for planned social change. Journal of Marketing, 46(1), 15-26.
SIMON, H.A. (1976). Administrative behavior: a study of decision making processes in administrative organizations. New York: Harper.
SKINNER, B.F. (1953). The behavior of organisms. New York: Appleton-Century-Crofts.
STERN, P.C. (1992). Psychological dimensions of global environmental change. Annual Review of Psychology, 43, 269-302.
VLEK, C.A.J. (1989). Modellen en methoden voor het begrijpen en verbeteren van beslissingen (Models and methods to understand and improve decision making). In: C.W.F. Van Knippenberg, and J.A. Michon (Eds.). Handboek Sociale Verkeerskunde (Handbook of social traffic science). Assen/Maastricht: Van Gorcum.
VLEK, C.A.J. (1995). Technical versus socio-behavioral solutions to environmental problems: psychology's unexploited potential. Extended version of an invited lecture for the Environmental Psychology Division of the American Psychological Association, presented in New York, August 1995.
VLEK, C.A.J., Michon, J.A. (1991). Why we should and how we could decrease the use of motor vehicles in the near future. Journal of International Association of Traffic and Safety Sciences, 15, 82-93.
WILSON, S.W. (1985). Knowledge growth in an artificial animal. In: J.J. Grefenstette (Ed.). Proceedings of the International Conference on Genetic Algorithms and their Application. Pittsburgh PA: Lawrence Erlbaum. pp. 16-23.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999