José Castro Caldas and Helder Coelho (1999)
Journal of Artificial Societies and Social Simulation vol. 2, no. 2, <https://www.jasss.org/2/2/1.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 2-Feb-99 Accepted: 10-Mar-99 Published: 14-Apr-99
![]()
 Abstract
AbstractAs it seems to me, the feelings of which a man is capable are of various grades. He is always subject to mere physical pleasure or pain [...]. He is capable also of mental and moral feelings of several degrees of elevation. A higher motive may rightly overbalance all considerations belonging even to the next lower range of feelings; but so long as the higher motive does not intervene, it is surely both desirable and right that the lower motives should be balanced against each other[...]. Motives and feelings are certainly of the same kind to the extent that we are able to weigh them against each other; but they are, nevertheless, almost incomparable in power and authority.My present purpose is accomplished in pointing out this hierarchy of feeling, and assigning a proper place to the pleasures and pains with which the Economist deals. It is the lowest rank of feeling which we here treat. [...] Each labourer, in the absence of other motives, is supposed to devote his energy to the accumulation of wealth. A higher calculus of moral right and wrong would be needed to show how he may best employ that wealth for the good of others as well as himself. But when that higher calculus gives no prohibition, we need the lower calculus to gain us the utmost good in matters of moral indifference.
begin
t<- 0
randomly generate a population P(t)
determine aggregate results for P(t)
t<- t+1
while not(stopping criteria) do
begin
for every agent j do
begin
assign credit to rule sets in P(t)
select a rule set aj1 from P(t)
if r < prob_crossj then
begin
select a rule set aj2 from P(t)
crossover(aj1, aj2) to a'j
end
for every bit in a'j
if r <prob_mutj then mutate that bit
end
determine aggregate results for P(t)
t <- t+1
end
end
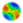
|
| Figure 1: Co-ordination (problem 1): Choice frequency per colour through the simulation |
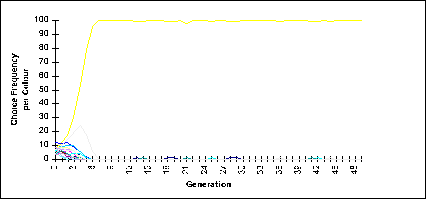
|
| Figure 2: Co-ordination (problem 2): Choice frequency per colour through the simulation |
we observe, as expected, a process of convergence. In the run reported in figure 2, choices that are Pareto inefficient (colours b and e) compete at the beginning of the simulation, and colour b that was not the most frequent in the initial population finally defeats colour e. Five of ten runs of the simulation with different initial populations converged to the Pareto optimal choice, the remaining simulations converged to a Pareto inferior outcome. Once again an invisible hand guides the agents, except that now it may lead them to an outcome that is not the best possible. We may conjecture, however, that if we would let the players discuss and agree on a joint strategy the chances of co-ordination in a Pareto optimal choice would increase.
There are many theories. One, the economic/game-theoretical prediction, is that no one will ever contribute anything. Each potential contributor will try to "free-ride" on the others. [...] Another theory, which I will call the sociological-psychological prediction, is that each subject will contribute something [...] it is some times claimed that altruism, social norms or group identification will lead each to contribute [...x...], the group optimal outcome. [...] Examination of the data reveals that neither theory is right.As a matter of fact, the experimental evidence in similar cases shows that, with large groups, positive posted contributions are observable in the first rounds but free-riding soon emerges leading the group to levels of contribution that all agents consider undesirable.
The collective return on investment is given by:
![]()
The apportioning rule is:
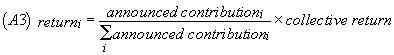
The credit assignment function is:
![]()
and the collective payoff is given by:
![]()
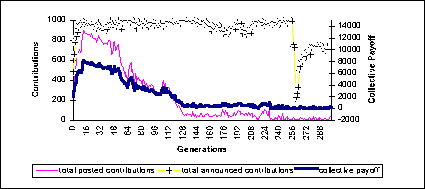
|
| Figure 3: probability of monitoring = 0. Contributions and collective payoffs through the simulation |
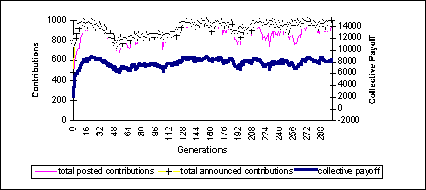
|
| Figure 4: probability of monitoring = 1. Contributions and collective payoffs through the simulation |
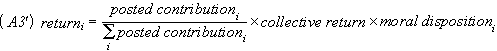
with the implicit penalty reverting to the meta-agent and included in the collective payoff. The meta-agent chooses the individuals to be inspected by a simple rule: if r (a random real between 0 and 1) is lower than probability of monitoring (a parameter of the simulation), then agent i's envelope will be opened.
![]()
For non-monitored actions, under both regimes, the credit of action i to agent j is assigned by:
![]()
and for monitored actions with contributioni < 35 we have
![]()
with ![]() .
.
The collective payoff is given by (A5), and the size of one agent is updated according to:
![]()
The simulation includes a training period of 100 generations during which no voting takes place and which is used by the agents to explore the regimes of the two rules, assigning values to them. Rule 2 is experienced in the initial fifty generations and rule 1 throughout the next fifty. In generation 101, and every 20 generations after that, a vote takes place that may change the rule regime.
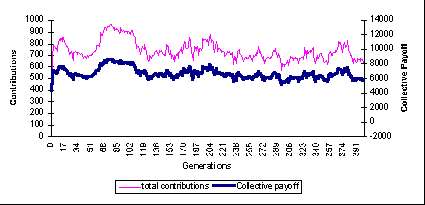
|
| Figure 5: all agents created equal: contributions and collective payoffs through the simulation |
|
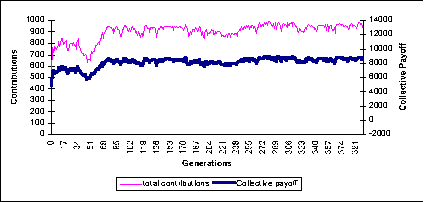
| Figure 6: distributed power: contributions and collective payoffs through the simulation |
|
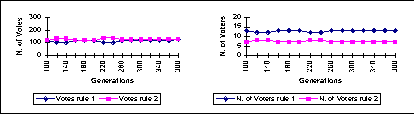
| Figure 7: distributed power: number of votes and voters |
2 Arifovic's use of the GA has been discussed by Chattoe (1998) and in Caldas and Coelho (1999).
3 P(t) stands for the population in generation t, r is a uniformly distributed random number between 0 and 1; prob_crossj and prob_mutj are the parameters that set the probability of crossover of a selected chromosome and the probability of mutation of each single bit for agent j.
4 Even though in this particular context mutation is hardly justifiable in rational terms, note that instability in convergence is also observable with human beings in similar experimental contexts; boredom or insufficient understanding of the game situation are usually the explanations given by researchers. The authors thank an anonymous referee for pointing out that an important feature, that has been experimentally observed is not captured by the model: some strategies, for instance 'black' and 'white' strategies, may be prominent. In multiple runs in the laboratory they would be observed as outcomes with a non-random frequency.
5 In all the simulations that follow, the Population Size is 20, the Probability of Crossover is 0.5 and the Probability of Mutation is 0.01, for all agents.
6 Different initial populations were generated using various random generator seeds. The observed overall pattern of outcome is common to all.
ALCHIAN, Armen A. and Demsets H. (1972), "Production, Information Costs, and Economic Organization". American Economic Review, vol. 62, December 1972, pp 777-795.
ARIFOVIC, Jasmina (1991), Learning by Genetic Algorithms in Economic Environments. Doctoral Dissertation, Department of Economics, Chicago: University of Chicago.
ARTHUR, Brian (1994), Increasing Returns and Path Dependence in the Economy. Ann Arbor, Michigan: University of Michigan Press.
CALDAS, José C. and Coelho H. (1994), "The Simulation of Trade in Oligopolistic Markets". In Doran J. and Gilbert, N. (Eds.) Simulating Societies: The Computer Simulation of Social Phenomena. London: UCL Press.
CALDAS, José C. and Coelho H. (1999), "Agents, Groups and Institutions", Working Paper, DINAMIA/ISCTE, (forthcoming).
CASTELFRANCHI, Cristiano (1998). "Simulating with Cognitive Agents: The Importance of Cognitive Emergence". Pre-Proceedings MABS'98 (Multi-agent systems and Agent-Based Simulation). July 4-6, 1998, Cité des Sciences - La Villette, Paris, France.
CHATTOE, Edmund (1998), "Just How (Un)realistic are Evolutionary Algorithms as Representations of Social Processes". Journal of Artificial Societies and Social Simulation (JASSS), vol. 1, no. 3, https://www.jasss.org/1/3/2.html.
CONTE, Rosario and Castelfranchi, C., (1995), Cognitive and Social Action. London: UCL Press.
DAVIS, Paul (1985), "Clio and the Economics of QWERTY". American Economic Review, n. 75, pp. 332-337.
FABER, Malte and Proops, John, Evolution, Time, Production and the Environment. Third Revised and Enlarged Ed. Berlin: Spriger. EDGEWORTH, F.Y. (1881), Mathematical Psychics. London: Kegan Paul.
GILBERT, Nigel (1995), "Simulation: an emergent perspective". 7/28/98, http://www.soc.surrey.ac.uk/research/simsoc/tutorial.html.
GOLDBERG, David E. (1989), Genetic Algorithms in Search, Optimization and Machine Learning. Reading, Massachusets: Addison-Wesley.
HAYEK, Friedrich A. (1973), Law, Legislation and Liberty, Vol. 1 - Rules and Order. Chicago: The University of Chicago Press.
HEAP, S.H., Hollis, M., Lyons, B., Sugden, R., and Weale A. (1992), The Theory of Choice: A Critical Guide. Oxford UK: Blackwell.
HODGSON, Geoffrey M. (1988), Economics and Institutions: A Manifesto for a Modern Institutional Economics. Cambridge, UK: Polity Press.
HODGSON, Geoffrey M. (1993), Economics and Evolution: Bringing Life Back Into Economics. Cambridge, UK: Polity Press.
HOLLAND, John H. (1975), Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence. Second edition, Cambridge, Massachusetts: The MIT Press, 1992.
JEVONS, W. S. (1871), The Theory of Political Economy. Reprints of Economic Classics, New York: Augustus M. Kelley, 1965.
LEDYARD, John O. (1995), "Public Goods: A Survey of Experimental Research". In John Kagel and Alvin Roth (Eds.), The Handbook of Experimental Economics, Priceton, New Jersey: Princeton University Press.
MACY, Michael W. (1998), "Social Order in Artificial Worlds". Journal of Artificial Societies and Social Simulation (JASSS), vol. 1, no. 1, https://www.jasss.org/1/3/2.html.
MARGOLIS, Howard (1991), "A New Model of Rational Choice". In Rational Choice Theory, Aldershot: Edward Elgar Publishing.
NORTH, Douglass C. (1990), Institutions, Institutional Change and Economic Performance. 5th edition, Cambridge: Cambridge University Press.
OLSON, Mancur (1965), The Logic of Collective Action. Cambridge, Massachsets: Harvard University Press.
SIMON, Herbert (1955), "A Behavioral Model of Rational Choice". Quarterly Journal of Economics, n. 69, pp. 99-118.
SIMON, Herbert (1956), "Rational Choice and the Structure of the Environment". Psychological Review, n. 63, pp. 129-138.
SUGDEN, Robert (1986), The Economics of Rights, Co-operation, and Welfare. Oxford: Blackwell.
VANBERG, Viktor J. (1994), Rules and Choice in Economics. London: Routledge.
WILLIAMSON, Oliver E. (1985), The Economic Institutions of Capitalism. First Paperback Edition, New York: The Free Press, 1987.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1999