Cooperation in the Prisoner's Dilemma Game Based on the Second-Best Decision
Journal of Artificial Societies and Social Simulation
12 (4) 7
<https://www.jasss.org/12/4/7.html>
For information about citing this article, click here
Received: 31-Jan-2008 Accepted: 19-Jul-2009 Published: 31-Oct-2009
 Abstract
Abstract

|
| Table 1. Payoff matrix of the prisoner's dilemma game |
|
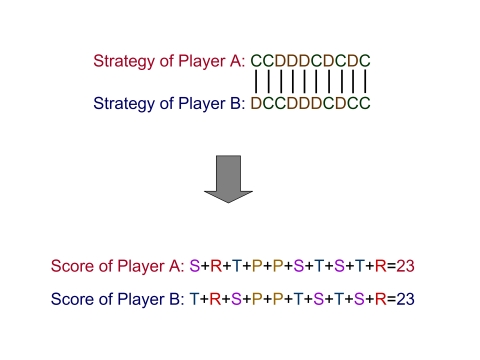
| Figure 1. Illustration of the sequential prisoner's dilemma game |
|
|
(1) |
|
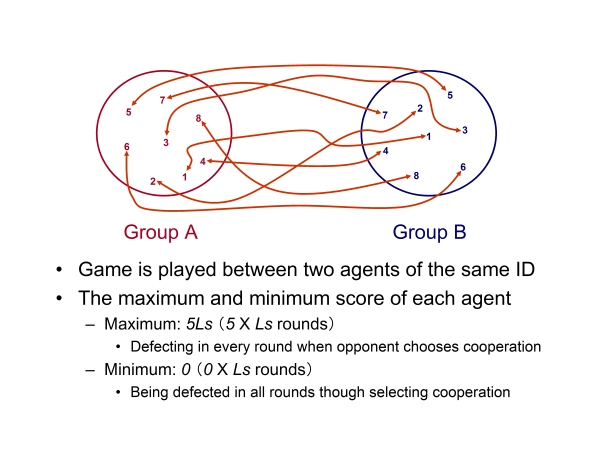
| Figure 2. Outline of the model |
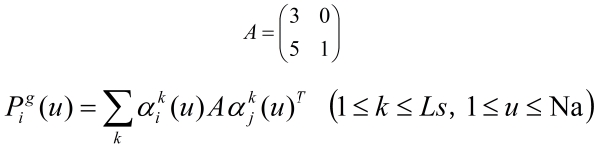
|
(2) |
|
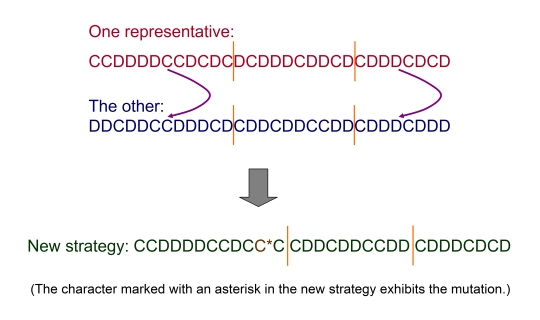
| Figure 3. Illustration of the evolutionary process |
|
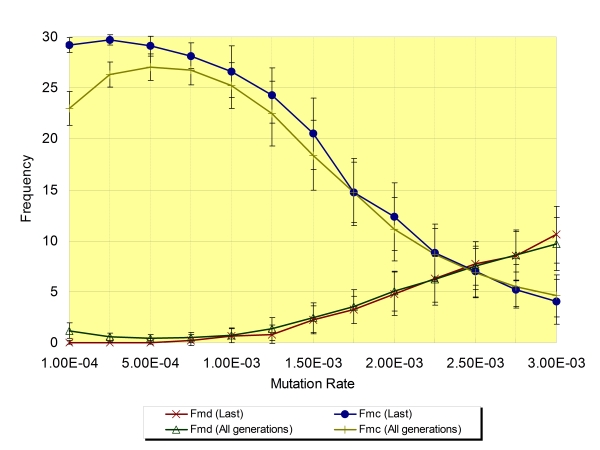
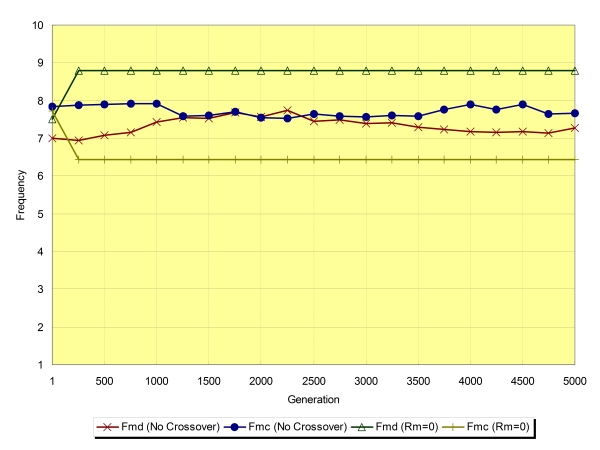
| Figure 4. The dependence of the frequency of mutual defection (Fmd) and mutual cooperation (Fmc) on mutation rate (Rm) regarding the average of the last generation and all generations (Na=8, Ls=30, ±SD) |
|
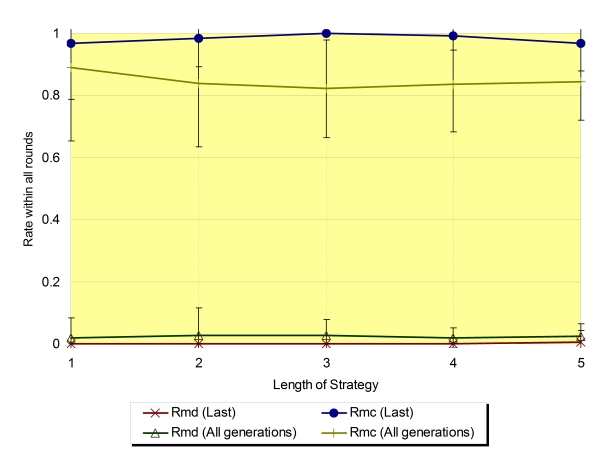
| Figure 5. The rate of mutual defection (Rmd) and mutual cooperation (Rmc) (Na=2, Ls=1 to 5, ±SD) regarding the average of the last generation and all generations |
|
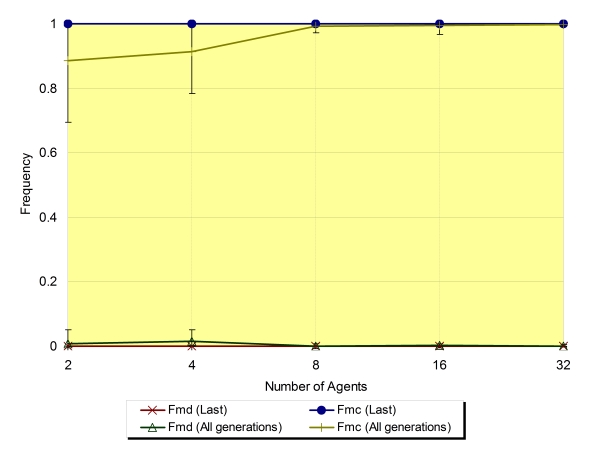
| Figure 6. This figure show the dependence of the frequency of mutual defection (Fmd) and mutual cooperation (Fmc) on Na (Na=2 to 32, Ls=1, ±SD). In this case, the game takes the form of the simple prisoner's dilemma game |
|
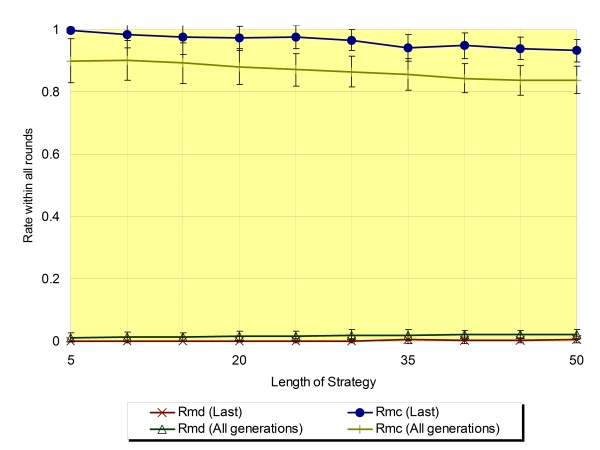
| Figure 7. The rate of mutual defection (Rmd) and mutual cooperation (Rmc) regarding the average of the last generation and all generations (Na=4,±SD) |
|
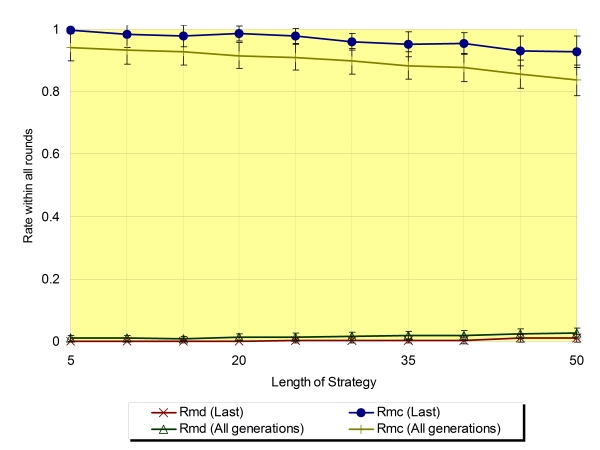
| Figure 8. Rmd and Rmc regarding the average of the last generation and all generations (Na=8,±SD) |
|
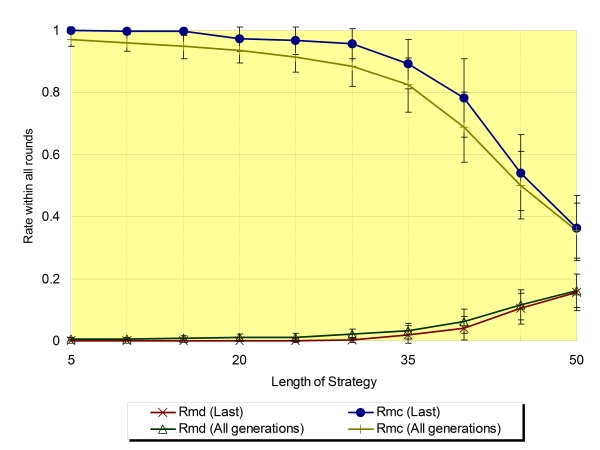
| Figure 9. Rmd and Rmc regarding the average of the last generation and all generations (Na=16,±SD) |
|
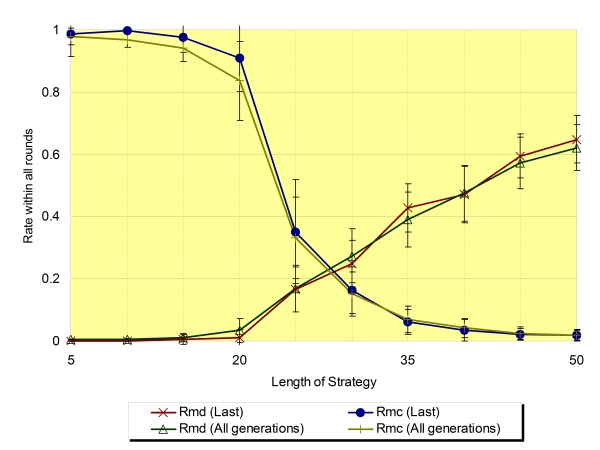
| Figure 10. Rmd and Rmc regarding the average of the last generation and all generations (Na=32,±SD) |
|
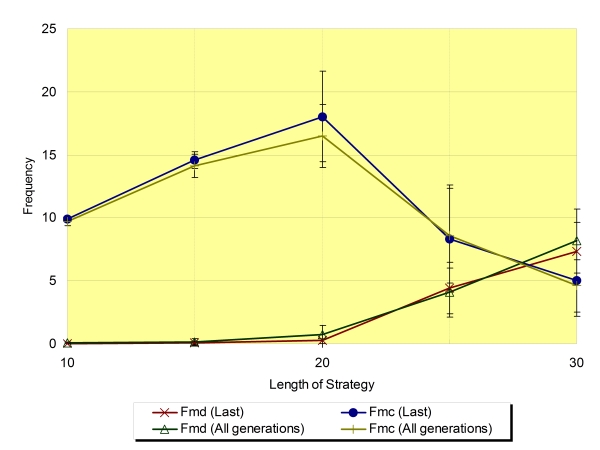
| Figure 11. The frequency of mutual defection (Fmd) and mutual cooperation (Fmc) around the critical value of Ls regarding the average of the last generation and all generations (Na=8,±SD) |
|
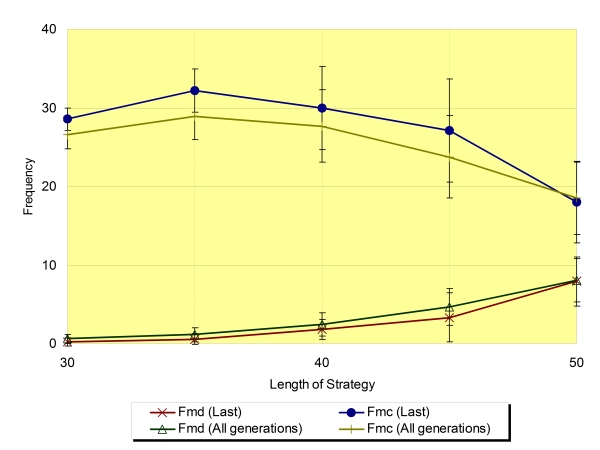
| Figure 12. Fmd and Fmc around the critical value of Ls regarding the average of the last generation and all generations (Na=16,±SD) |
|
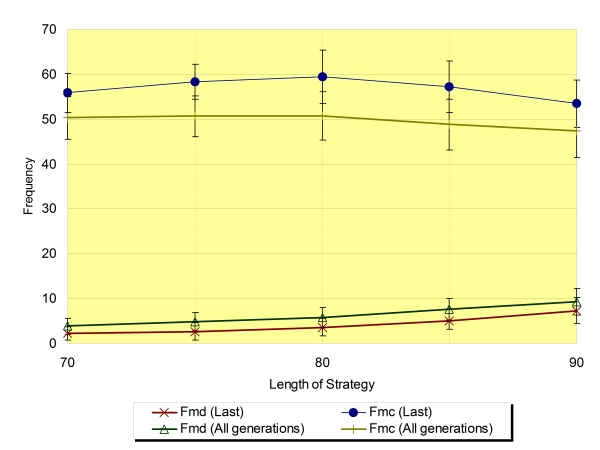
| Figure 13. Fmd and Fmc around the critical value of Ls regarding the average of the last generation and all generations (Na=32,±SD) |
|
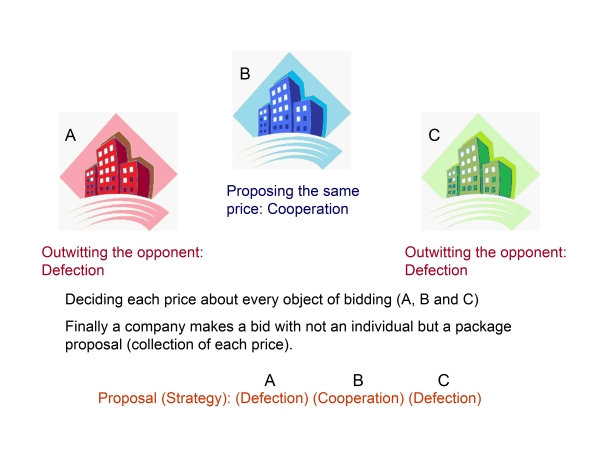
| Figure 14. Introduction of specific manner bidding |
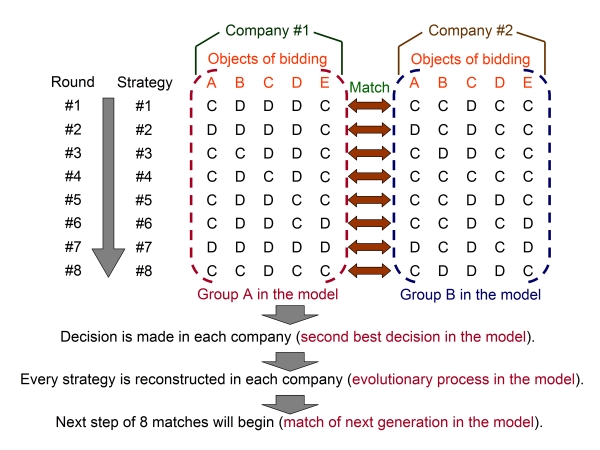
|
| Figure 15. Correspondence between the particular bidding and the model |
|
| Figure 16. |
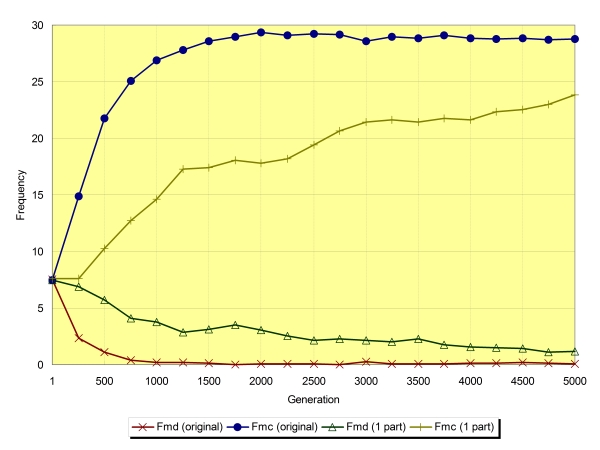
|
| Figure 17. |
Function Main:
Start:
// The number of groups equals two in this research.
for number_of_generations (<= from 1,000 to 5,000):
for group_id (<= number_of_groups):
Play_Match (group_id):
Update_Strategy (group_id):
end for:
end for:
End:
Function Play_Match (Group_ID):
Start:
// The sequential prisoner's dilemma game is played between the agents
// of the same id.
// The number of total game is equal to the number of opponent groups.
// The number of opponent groups equals one in this research.
for opponent_group_id (<= number_of_opponent_groups):
for agent_id (<= number_of_agents, Na):
for rounds (<= length_of_strategy, Ls):
if Strategy[Group_ID][agent_id][rounds] == D and
Strategy[opponent_group_id][agent_id][rounds] == C then:
Score[Group_ID][agent_id]
= Score[Group_ID][agent_id] + 5:
end if:
else if Strategy[Group_ID][agent_id][rounds] == C and
Strategy[opponent_group_id][agent_id][rounds] == C then:
Score[Group_ID][agent_id]
= Score[Group_ID][agent_id] + 3:
end else if:
else if Strategy[Group_ID][agent_id][rounds] == D and
Strategy[opponent_group_id][agent_id][rounds] == D then:
Score[Group_ID][agent_id]
= Score[Group_ID][agent_id] + 1:
end else if:
else:
Score[Group_ID][agent_id]
= Score[Group_ID][agent_id] + 0:
end else:
end for:
end for:
end for:
// Final score about the strategy of agent is the average of all Sequential PDGs.
for agent_id (<= Na):
Score[Group_ID][agent_id]
= Score[Group_ID][agent_id] / number_of_opponent_groups:
end for:
End:
Function Update_Strategy (Group_ID):
Start:
// All strategies of agents about the group are graded by their score.
Grade_Strategy:
// The strategy of the second grade in the group is selected as the representative
// strategy. The representative agent ID (=strategy ID) is decided.
representative_agent_id = agent_id (with the second grade strategy):
// Note. Both values of the length_of_fraction_1 (Lf1) and the
// length_of_fraction_2 (Lf2) are randomly changes in every step.
// The Lf1 and the Lf2 are less than Ls. The Lf1 is smaller than the Lf2.
// The representative strategy is partly duplicated to every strategy as follows.
for agent_id (<= Na, not equal to the representative agent ID):
for rounds_1 (<= Lf1):
Strategy[Group_ID][agent_id][rounds_1] =
Strategy[Group_ID][representative_agent_id][rounds_1]:
end for:
for rounds_2 (Lf2 <= rounds_2 <= Ls):
Strategy[Group_ID][agent_id][rounds_2] =
Strategy[Group_ID][representative_agent_id][rounds_2]:
end for:
end for:
// The process of mutation is executed for every strategy of agent.
for agent_id (<= Na):
for rounds (<= Ls):
if (a value randomly generated is over the threshold) then:
if Strategy[Group_ID][agent_id][rounds] == C then:
Strategy[Group_ID][agent_id][rounds] = D:
end if:
else:
Strategy[Group_ID][agent_id][rounds] = C:
end else:
end if:
end for:
end for:
End:
ANDRES GUZMAN, R, Rodriguez-Sickert, C and Rowthorn, R (2007) When in Rome, do as the Romans do: the coevolution of altruistic punishment, conformist learning, and cooperation. Evolution and Human Behavior, 28, pp. 112-117.
AXELROD, R (1984) The Evolution of Cooperation. Basic Books, New York.
AXELROD, R (1997) The Complexity of Cooperation. Princeton University Press, Princeton.
BERNHARD, H, Fischbacher, U and Fehr, E (2006) Parochial altruism in humans. Nature, 442, pp. 912-915.
BSHARY, R and Grutter, A S (2006) Image scoring and cooperation in a cleaner fish mutualism. Nature, 441, pp. 975-978.
CAO, Z and Hwa, R C (1999) Phase transition in evolutionary games. Int. Jour. of Mod. Phys. A, 14, pp. 1551-1560.
CRAIG MACLEAN, R and Gudelj, I (2006) Resource competition and social conflict in experimental populations of yeast. Nature, 441, pp. 498-501.
DAWES, C T, Fowler, J H, Johnson, T, McElreath, R and Smirnov, O (2007) Egalitarian motives in humans. Nature, 446, pp. 794-796.
FEHR, E and Gachter, S (2002) Altruistic punishment in humans. Nature, 415, pp. 137-140.
FEHR, E and Rockenbach, B (2003a) Detrimental effects of sanctions on human altruism. Nature, 422, pp. 137-140.
FEHR, E and Fischbacher, U (2003b) The nature of human altruism. Nature, 425, pp. 785-791.
FIEGNA, F, Yu, Yuen-Tsu N, Kadam, S V and Velicer, G J (2006) Evolution of an obligate social cheater to a superior cooperator. Nature, 441, pp. 310-314.
FORT, H (2003) Cooperation with random interaction and without memory or "tags". Journal of Artificial Societies and Social Simulation 6 (2) 4 https://www.jasss.org/6/2/4.html.
FORT, H and Sicardi, E (2007) Evolutionary Markovian strategies in 2×2 spatial games. Physica A, 375, pp. 323-335.
FOWLER, J H (2005) Altruistic punishment and the origin of cooperation. Proc. Natl. Acad. Sci. USA, 102, pp. 7047-7049.
GRAHAM, D and Marshall, R (1987) Collusive behavior at single-object second-price and English auctions, Journal of Political Economy, 95, pp. 1217-1239.
GRIFFIN, A S, West, S A and Buckling, A (2004) Cooperation and competition in pathogenic bacteria. Nature, 430, pp. 1024-1027.
HALES, D (2001) Tags produce cooperation in the prisoner's dilemma. Simulating Society V workshop: "The frontiers of social science simulation", Kazimierz Dolny, Poland.
HAUERT, C and Doebeli, M (2004) Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature, 428, pp. 643-646.
KIM, B J et al. (2002) Dynamic instabilities induced by asymmetric influence: prisoner's dilemma game on small-world networks. Phys. Rev. E, 66, 021907.
KRUEGER, F et al. (2007) The Neural Correlates of Trust. Proc. Natl. Acad. Sci. USA, 104, pp. 20084-20089.
KURZBAN, R, DeScioli, P and O'Brien, E (2007) Audience effects on moralistic punishment. Evolution and Human Behavior, 28, pp. 75-84.
MAYNARD SMITH, J (1982) Evolution and the Theory of Games. Cambridge University Press, Cambridge.
MCAFEE, P and McMillan, J (1992) Bidding rings, American Economic Review, 82, pp. 579-599.
MCNAMARA, J M, Barta, Z and Houston, A I (2004) Variation in behaviour promotes cooperation in the Prisoner's Dilemma game. Nature, 428, pp. 745-748.
NOWAK, M A and May, R M (1992) Evolutionary games and spatial chaos. Nature, 359, pp. 826-829.
NOWAK, M A and Sigmund, K (1998a) The dynamics of indirect reciprocity. J. Theor. Biol., 194, pp. 561-574.
NOWAK, M A and Sigmund, K (1998b) Evolution of indirect reciprocity by image scoring. Nature, 393, pp. 573-577.
NOWAK, M A, Sasaki, A, Taylor, C and Fudenberg, D (2004) Emergence of cooperation and evolutionary stability in finite populations. Nature, 428, pp. 646-650.
NOWAK, M A and Sigmund, K (2005) Evolution of indirect reciprocity. Nature, 437, pp. 1291-1298.
OHDAIRA, T, Ohashi, H, Chen, Y and Hashimoto, Y (2006) Partiality causes unhappiness: randomness of network induces difficulty in establishing cooperative relationship. The First World Congress on Social Simulation (WCSS06), Kyoto, Japan.
OHDAIRA, T and Ohashi, H (2007) The effect of occasional rational decision on the cooperative relationship between groups. The Twelfth International Symposium on Artificial Life and Robotics (AROB 12th '07), Beppu, Oita, Japan.
OHTSUKI, H, Hauert, C, Lieberman, E and Nowak, M A (2006) A simple rule for the evolution of cooperation on graphs and social networks. Nature, 441, pp. 502-505.
PANCHANATHAN, K and Boyd, R (2003) A tale of two defectors: the importance of standing for the evolution of reciprocity. J. Theor. Biol., 224, pp. 115-126.
PANCHANATHAN, K and Boyd, R (2004) Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature, 432, pp. 499-502.
RIOLO, R L (1997) The effects and evolution of tag-mediated selection of partners in populations playing the iterated prisoner's dilemma. Proc. of the 7th Int. Conf. on Genetic Algorithms (ICGA97), Morgan Kaufmann, San Francisco, pp. 378-385.
RIOLO, R L, Cohen, M D C and Axelrod, R (2001) Evolution of cooperation without reciprocity. Nature, 414, pp. 441-443.
ROCKENBACH, B and Milinski, M (2006) The efficient interaction of indirect reciprocity and costly punishment. Nature, 444, pp. 718-723.
RUTTE, C and Taborsky, M (2007) Generalized reciprocity in rats. PLoS Biol. 5(7): e196 doi:10.1371/journal.pbio.0050196.
SAIJO, T, Une, M and Yamaguchi, T (1996) Dango experiments, Journal of Japanese and International Economics, 10, pp. 1-11.
SEO, Y G, Cho, S B and Yao, X (2000) The impact of payoff function and local interaction on the n-player iterated prisoner's dilemma. Knowledge and Information Systems, 2, pp. 461-478.
STEPHENS, D W, McLinn, C M and Stevens, J R (2002) Discounting and reciprocity in an iterated prisoner's dilemma. Science, 298, pp. 2216-2218.
TANKERSLEY, D, Jill Stowe, C and Huettel, S A (2007) Altruism is associated with an increased neural response to agency. Nature Neuroscience, 10, pp. 150-151.
TURNER, P E and Chao, L (1999) Prisoner's dilemma in an RNA virus. Nature, 398, pp. 441-443.
TURNER, P E and Chao, L (2003) Escape from prisoner's dilemma in RNA phage Φ6. The American Naturalist, 161, pp. 497-505.
WARNEKEN, F, Hare, B, Melis, A P, Hanus, D and Tomasello, M (2007) Spontaneous altruism by chimpanzees and young children. PLoS Biol. 5(7): e184 doi:10.1371/journal.pbio.0050184.
YAO, X and Darwen, P J (1994) An experimental study of n-person iterated prisoner's dilemma games. Informatica, 18, pp. 435-450.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2009]