On the Effects of Skill Upgrading in the Presence of Spatial Labor Market Frictions: An Agent-Based Analysis of Spatial Policy Design
Journal of Artificial Societies and Social Simulation
12 (4) 5
<https://www.jasss.org/12/4/5.html>
For information about citing this article, click here
Received: 06-Aug-2009 Accepted: 20-Aug-2009 Published: 31-Oct-2009
 Abstract
Abstract| Table 1: Agents and their role in the model | ||
| Active Agents | Households | Consumption Goods Market: Role of Buyer Labor Market: Role of Worker |
| Consumption Goods Producer | Investment Goods Market: Role of Buyer Consumption Goods Market: Role of Seller Labor Market: Role of Employer | |
| Passive Agents | Malls | Consumption Goods Market: Information Transfer between Producers and Households |
| Capital Goods Producer | Investment Goods Market: Role of Seller | |
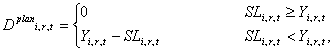
|
(1) |
where Yi,r,t is the smallest value Y ≥ 0 that satisfies
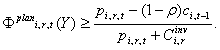
|
(2) |
Here ci,t-t denotes unit costs of production for firm i in the previous period, pi,r,t the prices of the consumption good, and ρ the discount factor. The sum of the orders received by all malls becomes
|
|
(3) |
|
|
(4) |
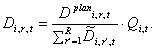
|
(5) |
Production times of consumption goods are not explicitly taken into account and the produced quantities are delivered on the same day when production takes place. The local stock levels at the malls are updated accordingly.
|
|
(6) |
where Ki(0) = 0 and Ii,t > 0 is the gross investment.
|
|
(7) |
where we denote with Ai,t the average quality of the capital stock. The function χ is increasing in the general skill level of the worker. Note that this formulation captures the fact that in the absence of technology improvements marginal learning curve effects per time unit decrease as experience is accumulated and the specific skills of the worker approaches the current technological frontier.
|
|
(8) |
where Bi,t denotes the average specific skill level in firms and α + β = 1
|
|
(9) |
Taking into account the above production function this yields under the assumption of positive investments
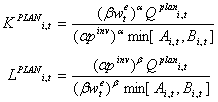
|
(10) |
and if Ki,tPLAN ≥ (1 - δ)Ki,t-1 the desired capital and labor stocks read Ki,tPLAN= Ki,tplan and Li,tPLAN= Li,tplan. Otherwise, we have
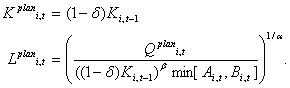
|
(11) |
|
|
(12) |
where ci,t-1 denotes unit costs in production of firm i in the previous period. Once the firm has determined the updated prices pi,r,t for all regions r where it offers its goods, the new prices are sent to the regional malls and posted there for the following period.
|
|
(13) |
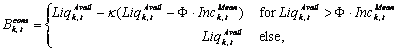
|
(14) |
where φ ≤ 1 is the percentage of the mean income such that a household spends all cash on hand below that level, and Inck,tMean is the mean individual (labor) income of an agent over the last periods. By definition the saving propensity fulfills 0 < κ < 1.
|
|
(15) |
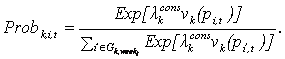
|
(16) |
Thus, consumers prefer cheaper products and the intensity of competition in the market is parameterized by λkcons. Once the consumer has selected a good he spends his entire budget Bk,weekt for that good if the stock at the mall is sufficiently large. In case the consumer cannot spend all his budget on the product selected first, he spends as much as possible, removes that product from the list Gk,weekt, updates the logit values and selects another product to spend the remaining consumption budget there. If he is rationed again, he spends as much as possible on the second selected product, rolls over the remaining budget to the following week and finishes the visit to the mall.
| Table 2: General skill distributions in the three different types of regions. | |||||
| General Skill Level | |||||
| Region | 1 | 2 | 3 | 4 | 5 |
| Low Skill | 0.8 | 0.05 | 0.05 | 0.05 | 0.05 |
| Medium Skill | 0.05 | 0.05 | 0.8 | 0.05 | 0.05 |
| High Skill | 0.05 | 0.05 | 0.05 | 0.05 | 0.8 |
| Table 3: Parameter settings | ||
| Description | Parameter | Value |
| Number of households: | 400 | |
| Number of firms | 10 | |
| Number of regions | 2 | |
| Labor Intensity of Productions | α | 0.662 |
| Capital Intensity of Production | β | 0.338 |
| Innovation probability | γinv | 0.1 |
| Depreciation rate of capital | δ | 0.01 |
| Monthly Discount factor | ρ | 0.95 |
| Mark-up factor | 1/(|η|-1) | 0.2 |
| Wage update | Φi | 0.02 |
| Reservation wage update | ψk | 0.02 |
| Minimal reservation wage | wRmin | 1 |
| Marginal saving propensity | κ | 0.1 |
| Intensity of choice by consumers | λkcons | 8.5 |
| Commuting costs | comm | 0.2 |
| Fraction of on-the-job searchers | φ0.1 | |
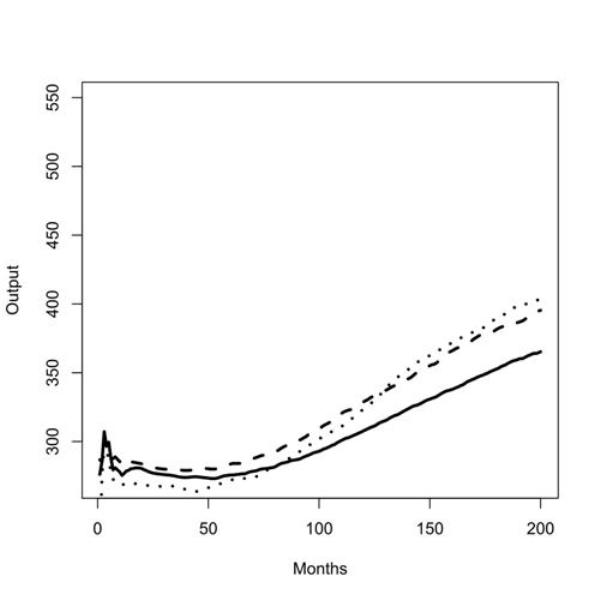 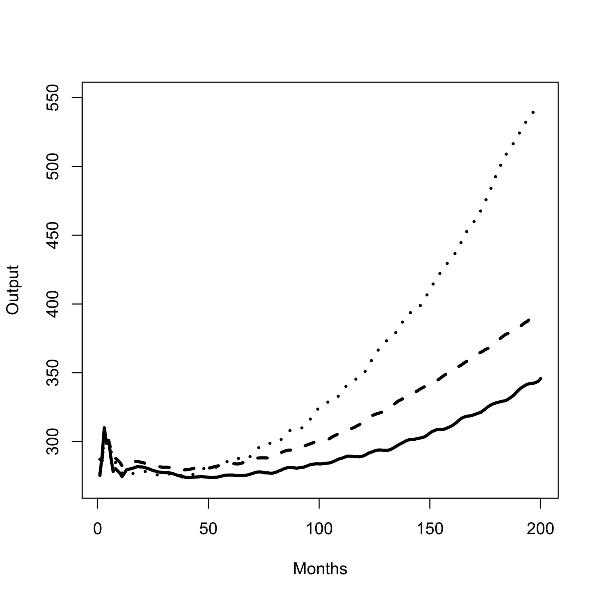
|
| Figure 1. Batch run with zero (left panel) and low (right panel) commuting costs for outputs in uniform low scenario (solid line), uniform medium scenario (dashed line), and low/high scenario (dotted line); |
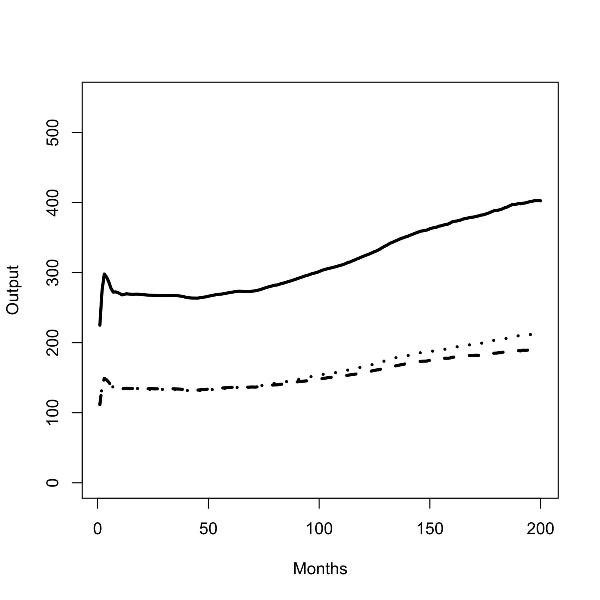 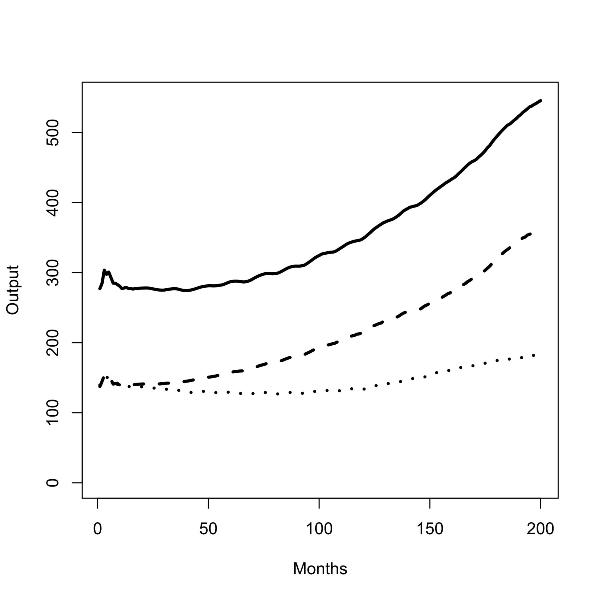
|
| Figure 2.Batch runs for zero (left panel) and low (right panel) commuting costs; total outputs (solid line), output in the low skill region (dashed line), output in the high skill regions (dotted line); |
| Table 4: Snapshots of average output for the three skill scenarios and two commuting cost levels. (Standard deviations in parentheses.) | ||||
| comm = 0 | ||||
| Month | 50 | 100 | 150 | 200 |
| low/ low | 293.95 (6.17) | 305.28 (22.09) | 330.79 (35.02) | 365.27 (55.66) |
| medium/ medium | 280.20 (8.90) | 309.63 (23.03) | 355.10 (38.86) | 395.36 (84.66) |
| low/ high | 266.40 (6.05) | 301.67 (36.41) | 362.77 (78.13) | 402.71 (169.30) |
| comm = 0.05 | ||||
| Month | 50 | 100 | 150 | 200 |
| low/ low | 274.07 (4.13) | 283.74 (15.33) | 306.17 (27.67) | 345.80 (42.06) |
| medium/ medium | 280.75 (8.92) | 300.31 (21.11) | 342.10 (37.63) | 393.48 (59.81) |
| low/ high | 281.35 (8.17) | 324.55 (47.50) | 410.61 (130.00) | 545.70 (451.20) |
| Table 5: Test for statistically significant differences between the output levels of the skill scenarios by pairwise comparison: p values of the Wilcoxon rank sum test. | ||||
| comm = 0 | ||||
| Month | 50 | 100 | 150 | 200 |
| low/ low vs. medium/ medium | <0.0001 | <0.0001 | 0.0008 | 0.0133 |
| low/ low vs. low/ high | <0.0001 | 0.6016 | 0.0677 | 0.0206 |
| medium/ medium vs. low/ high | <0.0001 | 0.0058 | 0.4616 | 0.7028 |
| comm = 0.05 | ||||
| Month | 50 | 100 | 150 | 200 |
| low/ low vs. medium/ medium | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| low/ low vs. low/ high | <0.0001 | <0.0001 | <0.0001 | 0.0002 |
| medium/ medium vs. low/ high | 0.4535 | 0.0254 | 0.007 | 0.3252 |
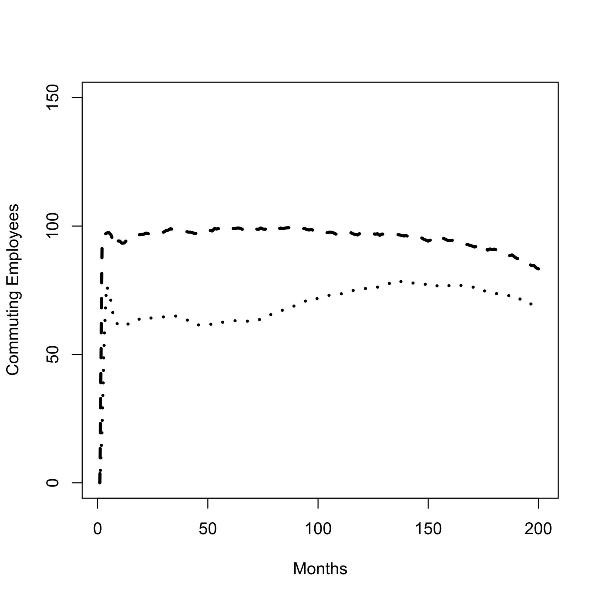 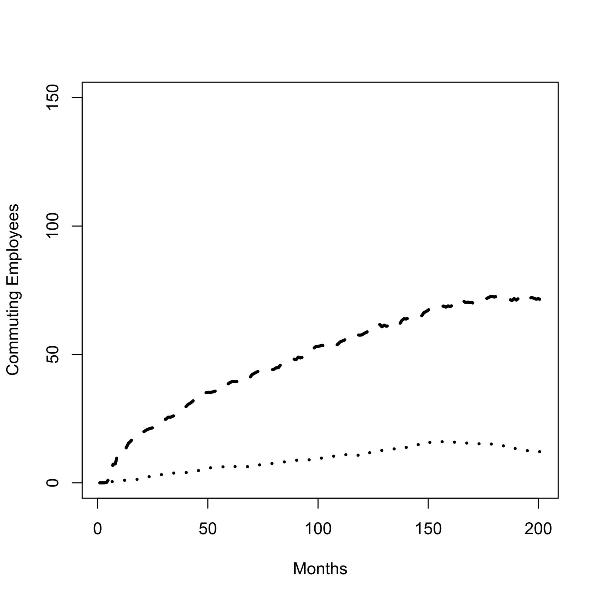
|
| Figure 3.Batch runs for zero (left panel) and low (right panel) commuting costs; number of commuters from low to high skill region (dotted line), number of commuters from high to low skill region (dashed line); |
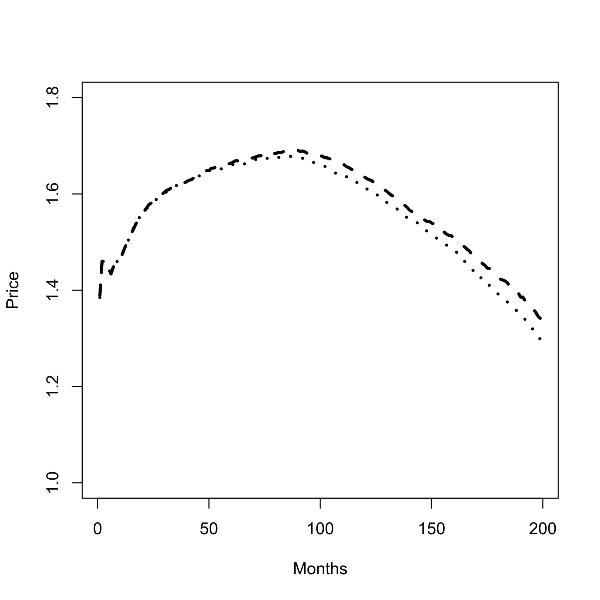 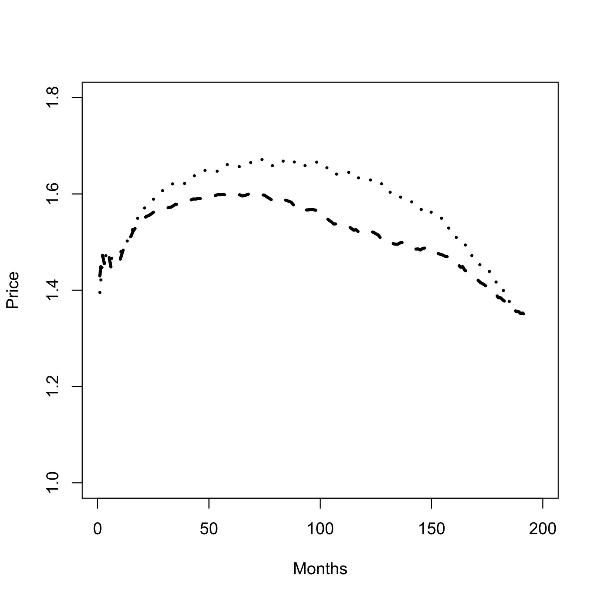
|
| Figure 4. Batch runs for zero (left panel) and low (right panel) commuting costs; prices in the low skill region (dashed line), prices in the high skill region (dotted line); |
|
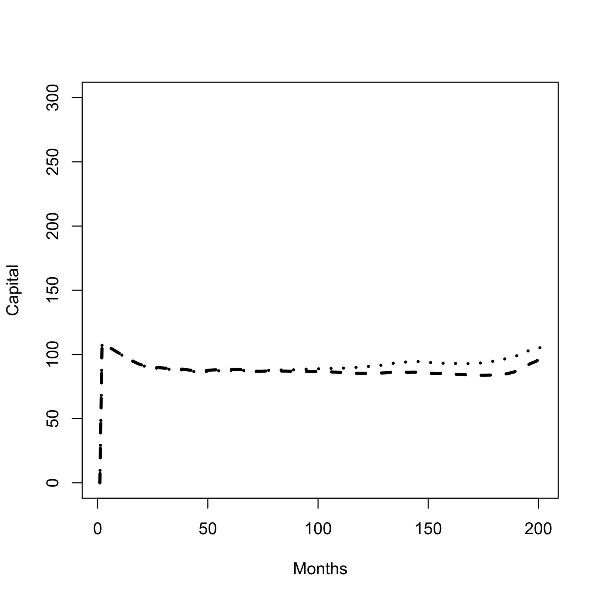
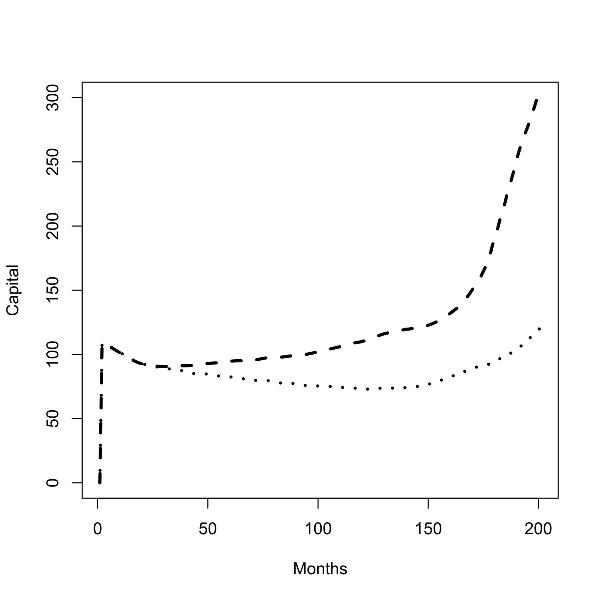
| Figure 5.Batch runs for zero (left panel) and low (right panel) commuting costs; capital stock in the low skill region (dashed line), capital stock in the high skill region (dotted line); |
|
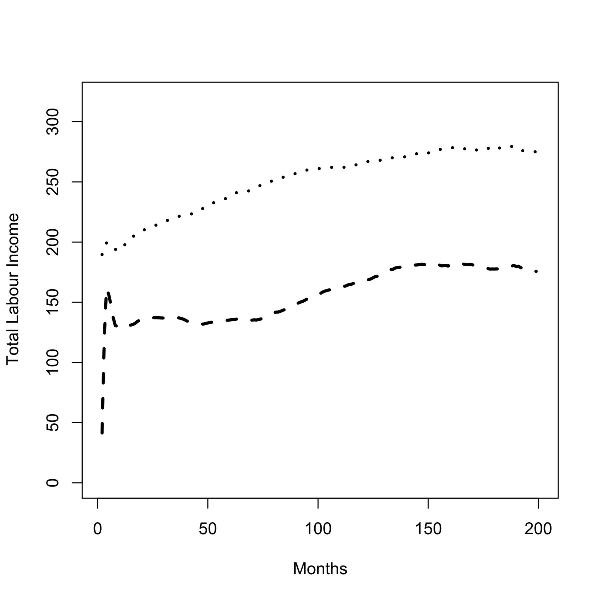
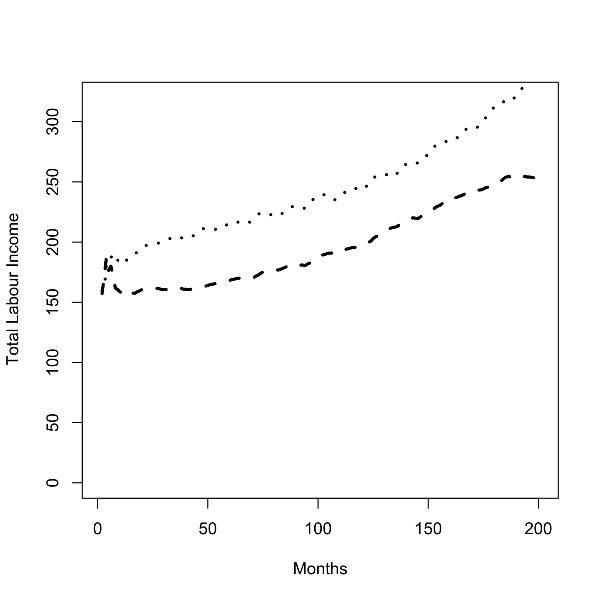
| Figure 6. Batch runs for zero (left panel) and low (right panel) commuting costs; total labor income of workers in the low skill region (dashed line) and the high skill region (dotted line). |
2It includes that Polish workers can obtain an unrestricted work permit in Germany. This permit is available for a border region of 50 km as long as the commuters reside in their home country and do not work more than two days per week in Germany.
3In the fully fledged EURACE model, a financial and a credit market will be added, and an exogenous energy market will constitute a proxy for the link to the 'rest-of-the-world' by affecting the production costs in the capital goods market.
4In the model each week consists of 5 days and each month of 4 weeks. Accordingly, each year has 240 days.
5In contrast, in the fully fledged EURACE platform, there is an explicit credit market model which can be appropriately linked to the real sectors considered here.
6In a more elaborate version savings will also be made dependent on the uncertainty over income.
8See, for instance, http://www.sachverstaendigenrat-wirtschaft.de/timerow/tabdeu.php.
9Note, that the differences between the low/high and medium/medium scenario for comm = 0.05 are significant until period 180 (at a level of significance of at least 90%). After period 180 the variance of the distribution sharply increases so that equality of means cannot be rejected based on the relatively low number of runs we performed.
10Due to space constraints we do not present the graph that demonstrates the wage differences between the regions.
ALECKE, B. and Untiedt, G. (2003). Pendlerpotentiale in den Grenzregionen an der EU-Aussengrenze. Beitrag zur International Summer School Economics of EU-Enlargement, University of Hohenheim.
ARGOTE, L. and Epple, D. (1990). Learning curves in manufacturing. Science, 247:920-924.
BASSANINI, A. and Scarpetta, S. (2002). Does human capital matter for growth in OECD countries? A pooled mean group approach. Economics Letters, 74(3):399-405.
BLACK, M. (1981). An empirical test of the theory of on-the-job-search. The Journal of Human Resources, 16:129-141.
BUNDESAMT, S. (2004). Volkswirtschaftliche Gesamtrechnung.
BUNDESAMT, S. (2006). Fachserie 18, 1.4 Inlandsproduktberechnung - Detaillierte Jahresergebnisse 2006.
BURDA, M. and Mertens, A. (2001). Estimating wage losses of displaced workers in Germany. Labour Economics, 8:15-42.
DAWID, H., Gemkow, S., Harting, S., Kabus, K., Neugart, M., and Wersching, K. (2008). Skills, innovation, and growth: an agent-based policy analysis. Journal of Economics and Statistics, 228:251-275.
DEATON, A. (1991). Saving and liquidity constraints. Econometrica, 59:1221-1248.
DEATON, A. (1992). Houshold saving in LDCs: Credit markets, insurance and welfare. Scandinavian Journal of Economics, 94:253-273.
DEISSENBERG, C., van der Hoog, S., and Dawid, H. (2008). Eurace: A massively parallel agent-based model of the European economy. Applied Mathematics and Computation, 204:541-552.
DIW (1994). Ost-West-Pendeln gehört zur Normalität des gesamtdeutschen Arbeitsmarktes. DIW-Wochenbericht, 51-52:861-866.
GEDDES, A. (2003). Still beyond fortress Europe? Patterns and pathways in EU migration policy. Queen's papers on Europeanisation, 4.
GUADAGNI, P. and Little, J. (1983). A logit model of brand choice calibrated on scanner data. Marketing Science, 2(3):203-238.
HILLIER, F. and Lieberman, G. (1986). Introduction to Operations Research. Holden-Day.
JOVANOVIC, B. and Nyarko, Y. (1995). A Baysian learning model fitted to a variety of empirical learning curves. Brooking Papers on Economic Activity, Microeconomics, 1995:247-305.
KIRMAN, A. (1992). Whom or what does the representative individual represent? Journal of Economic Perspectives, 6:117-136.
KRISHNAMRUTHI, L. and Raj, S. P. (1988). A model of brand choice and purchase quantity price sensitivities. Marketing Science, 7:1-20.
NAGLE, T. (1987). Strategy and Tactics of Pricing. Prentice Hall.
OECD (2004). Benefits and Wages: OECD indicators.
PISSARIDES, C. and Wadsworth, J. (1994). On-the-job-search, some empirical evidence. European Economic Review, 38:385-401.
ROSENFELD, C. (1977). The extent of job search by employed workers. Monthly Labor Review, 100:39-43.
SJAASTAD, L. (1962). The costs and returns of human migration. The Journal of Political Economy, 70(5):80-93. Part 2: Investment in Human Beings.
SMALL, I. (1997). The cyclicality of mark-ups and profit margins: Some evidence for manufacturing and services. Bank of England Working Paper.
TESFATSION, L. and Judd, K. E. (2006). Handbook of Computational Economics II: Agent-Based Computational Economics. North-Holland.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2009]