©Copyright JASSS

JASSS logo ----

Whan-Seon Kim (2009)

Effects of a Trust Mechanism on Complex Adaptive Supply Networks: An Agent-Based Social Simulation Study

Journal of Artificial Societies and Social Simulation 12 (3) 4
<https://www.jasss.org/12/3/4.html>

For information about citing this article, click here

Received: 31-Jan-2009    Accepted: 16-May-2009    Published: 30-Jun-2009

PDF version

* Abstract

This paper models a supply network as a complex adaptive system (CAS), in which firms or agents interact with one another and adapt themselves. And it applies agent-based social simulation (ABSS), a research method of simulating social systems under the CAS paradigm, to observe emergent outcomes. The main purposes of this paper are to consider a social factor, trust, in modeling the agents' behavioral decision-makings and, through the simulation studies, to examine the intermediate self-organizing processes and the resulting macro-level system behaviors. The simulations results reveal symmetrical trust levels between two trading agents, based on which the degree of trust relationship in each pair of trading agents as well as the resulting collaboration patterns in the entire supply network emerge. Also, it is shown that agents' decision-making behavior based on the trust relationship can contribute to the reduction in the variability of inventory levels. This result can be explained by the fact that mutual trust relationship based on the past experiences of trading diminishes an agent's uncertainties about the trustworthiness of its trading partners and thereby tends to stabilize its inventory levels.

Keywords:
Complex Adaptive System, Agent-Based Social Simulation, Supply Network, Trust

* Introduction

1.1
To survive in a rapidly changing competitive environment, many firms have built and maintained collaborative relationships with their customers and suppliers. Especially in the context of a supply chain, that is, firms linked together to produce and distribute a product or service from raw material supplier to customer, the effectiveness of collaboration is dependent on the firms' initiatives to build trust with the trading partner firms and their effective information management (Vlachos and Bourlakis 2006). Madlberger (2008) argues that an important prerequisite of interfirm collaboration in the supply chain context is information sharing, and interorganizational systems (IOS), i.e. electronic linkages between trading partners, have played a role as technological enablers for closer relationships and tighter coordination between them. Research based on embeddedness theory (Lin 2006) demonstrates the crucial role of trust for the adoption of IOS and Uzzi (1997) states that trust reinforces the exchange of sensitive information and joint problem-solving at the interorganizational level. Moreover, using the mold-manufacturing industry as an example, Lin et al. (2005) evaluate the effect of trust mechanisms on the performance of the mold-manufacturing supply chain. They show that the trust mechanisms improve the average cycle time and in-time order fulfillment rate, especially when the environment is highly changeable, at the expense of the material cost. However, the raised cost is controlled within an acceptable range and can be considered a premium paid for shortening the average cycle time, which implies that selecting trading partners based on trust mechanisms generally result in better supply chain performance.

1.2
From a modeling perspective[1], many researches in supply chain management (SCM) have focused on developing 'normative' models analyzing the benefits of sharing information globally, that is, across an entire supply chain. However, despite the benefits, firms are, in reality, still reluctant to participate in a regular exchange of business data, implying a gap between purported benefits and actual information sharing participation in practice (Madlberger 2008). Therefore, this paper proposes a 'descriptive' model analyzing decision-making behaviors of firms in a supply chain network (or simply called as supply network), with a more realistic assumption that they are not sharing information across the entire supply network, but are making decisions based on locally available information only, which has been a more widely-adopted practice in industry without the SCM disciplines. Moreover, given the dynamic and complex nature of a supply network, it is not enough to recognize it as simply a system. Therefore, as a conceptual framework for modeling a supply network, this paper adopts complex adaptive system (CAS) theory, which has recently enjoyed much interest in management fields including SCM.

1.3
Agent-based social simulation (ABSS) is a method of simulating social systems under the CAS paradigm that is gaining increasing acceptance and usage in academic literature. The basic idea of ABSS is to model human behaviors of decision-making in terms of software agents and simulate social phenomena on a computer. Given that a supply network can be modeled as a complex adaptive system with a diverse set of social agents and many dimensions of interactions based on their adaptive decision-making rules, the ABSS is an appropriate research method to apply to the in-depth analyses of supply networks.

1.4
The purposes of this paper are as follows. First of all, this paper considers a social variable, trust, in modeling the behavioral decision-making rules and associated interactions of agents or firms in a supply network. And then, it applies the ABSS to examine the intermediate self-organizing processes of agents and the resulting macro-level system behaviors, so-called 'emergent properties' in CAS theory, such as collaboration patterns. Finally, the effects of the agents' decision-making behaviors, reflecting the trust factor, on the performance of inventory management are analyzed.

1.5
This paper is organized as follows. In the literature review that follows, I will offer an overview of trust concepts, especially in the context of business relationships, and discuss conceptual frameworks about CAS and ABSS based on which supply network models can be developed. Building on this review, in the subsequent section, I propose models that outline trust relationships and associated behavioral decision-makings in a supply network context. In the next section, I describe simulation studies and analyze simulation results. Finally, I discuss their implications and conclude by outlining study limitations and further research issues.

* Theoretical Backgrounds and Literature Reviews

Trust concepts

2.1
Definitions on the concept of trust are various. However, according to Jarvenpaa et al. (1998), most researchers who base their studies on trust adopt the integrated view proposed by Mayer et al. (1995). They define trust as "the willingness of a party to be vulnerable to the actions of another party based on the expectation that the other will perform a particular action important to the trustor, irrespective of the ability to monitor or control that other party." The development of trust is contingent upon the context in which trust developing interactions occur or on the observer's point of view (Tykhonov et al. 2008). Because trust is based on prior experience, the level of trust, in the present, continuously changes. In other words, the quality of previous experience increases or decreases the level of trust in the partner (Abdul-Rahman and Hailes 2000).

2.2
The fact that trust is defined in terms of expectation, not confidence, reflects uncertainties about the partner's future behaviors. The presence of environmental uncertainty brings forth the need for trust (Iacobucci and Hibbard 1999). Therefore, trust is necessarily associated with taking risks. More specifically, Mayer et al. (1995) state "trust is not taking risk per se, but rather a willingness to take risk." Many other definitions of trust are based on similar views regarding willingness to undertake risk (Ishaya and Macaulay 1999). Predictability is a source of trust and requires repeated interaction through which one can learn more about the other party. Therefore, by sharing a variety of experiences, one's ability to predict the other's behavior improves and trust between the two grows (Doney and Cannon 1997).

2.3
Hart and Saunders (1997) expand the self-expectation notion, framed by Mayer et al. (1995), to the sense of reciprocity, explaining that trust is based on fair dealing and a sense of reciprocity. Also, Gouldner (1959) states that participants in a relationship desire reciprocity, therefore one is morally obligated to give something in return for something received. Their explanations imply the necessity to continuously evaluate whether the partner is dealing fairly and whether partner's level of reciprocity is adequate.

Trust in the context of business relationships

2.4
The notion of trust based on environmental uncertainty, predictability and reciprocity can also be applied to business relationships. Anderson and Narus (1990) explain the implication that trust has for business relationships as "the firm's belief that another company will perform actions that will result in positive outcomes for the firm, as well as not take unexpected actions that would result in negative outcomes for the firm."

2.5
Trust plays a critical role in the development of long-term relationships (Dwyer et al. 1987;Morgan and Hunt 1994) and a firm that trusts its business partner is more committed to and intends to stay in the relationship (Anderson and Weitz 1989;Morgan and Hunt 1994). These commitment and intention may be explained partly by the fact that trust between companies can lower transaction costs when trusted trade partners become preferred business partners (Akkermans 2001;Tykhonov et al. 2008). Dwyer et al. (1987) state that "even though short term inequities are inevitable in any relationship, through trust, parties in a relationship develop confidence that, over the long-term, short-term inequities will be corrected to yield a long-term benefit." Therefore, mutual trust is more likely than one-way trust (Anderson and Weitz 1989). Furthermore, Anderson and Weitz (1992) imply that, through repeated cyclical interactions between two firms, the trust levels in the mutual relationship become symmetrical in the long run. Asymmetrical trust levels probably result in unsatisfactory relationships because the less committed party who holds lower trust level is more willing to abandon the relationship and less willing to reciprocate sacrifices made by the more committed party who holds the higher trust level.

2.6
Trust is a cumulative product of repeated past interactions between two parties through which they come to understand each other and to evolve a common understanding of mutual commitments (Ring and Van de Ven 1994). Mutual commitments are not always based on legal contracts, but in some cases on psychological contracts which are naturally established in the process of repeated cyclical interactions between two firms. According to Ring and Van de Ven (Ring 1994), psychological contracts, as opposed to most legal contracts, consist of "unwritten and largely non-verbalized sets of congruent expectations and assumptions held by transacting parties about each other's prerogatives and obligations." They also state "informal norms and understandings of acceptable behavior stemming from reliance on trust compensated for the absence of a formal agreement and permitted the parties to proceed to execute the informal commitments implicit in their psychological contract."

2.7
Business partners who have had successful transactions in the past learn to build relationships that rely on trust. Higher frequencies of successful transactions increase the level of trust between them. Thus, reliance on trust will emerge only as a consequence of repeated market transactions between the parties (Ring and Van de Ven 1992). In short, recursive consequences of favorable performance outcomes enhance trust as well as continuity of the relationship (Iacobucci and Hibbard 1999). Thus, positive outcomes form a reinforcing feedback loop, inducing subsequent continued positive outcomes. Ultimately, inter-firm trust operates as a governance mechanism in the context of business relationships, characterized by uncertainty and dependence (Doney and Cannon 1997).

Complex adaptive system (CAS) and Agent-based social simulation (ABSS)

2.8
According to Holland (1995), complex adaptive system (CAS) is defined as "a system that emerges over time into a coherent form, and adapts and organizes itself without any singular entity deliberately managing or controlling it." For example, competing firms generating certain market patterns, a cross-functional team developing norms and rules of action, and the traffic configurations generated by vehicles on a roadway are all complex adaptive systems (Choi et al. 2001). CAS theory has recently been paid much attention in management and organizational fields. The concepts from CAS theory have been applied to examine phenomena such as organizational change and transformation, innovation, human resource practices, and strategy (Choi et al. 2001). They can also be employed to enrich the operations management (OM) including the supply chain management (SCM) (Pathak et al. 2007).

2.9
Agent-based approach has been applied to complexity studies in various fields such as biology, physics, sociology, economics and management including supply chain research. Parunak et al. (1998) state that "agent-based modeling is most appropriate for domains characterized by a high degree of localization and distribution, and dominated by discrete decision. Equation-based modeling is most naturally applied to systems that can be modeled centrally."

2.10
Agent-based social simulation (ABSS) is a method of simulating social systems under the CAS paradigm which is gaining increasing acceptance and usage in academic literature. According to Davidsson (2002), ABSS is developed based on three research areas, including agent-based computing, the social sciences, and computer simulation, and can be mainly used for the simulation of complex systems with much interaction between the entities of the system[2]. The basic idea of ABSS is to model human behaviors of decision-making in terms of software agents and simulate social phenomena on a computer.

2.11
Swarm, developed by the Santa Fe Institute, was the first widely used software toolkit for modeling complex adaptive systems. Since then, many more ABSS software toolkits have been developed and one of the widely used open source toolkits is Repast (Recursive Porous Agent Simulation Toolkit). Repast has been developed as a reusable software infrastructure to support "rapid social science discovery" based on extensive computational experimentation (Sallach and Macal 2001;Samuelson and Macal 2006). Repast has been used extensively in social simulations and related applications. Repast system, including the source code, is available at http://repast.sourceforge.net/. Repast is available in pure Java and pure Microsoft .NET forms. Users can develop simulation models by incorporating Repast library modules or classes into their own Java programs.

Applying CAS theories and ABSS methods to supply network

2.12
Firms linked together to produce and distribute a product or service from raw material supplier to customer is called supply chain, or supply network in case alternative suppliers and buyers are considered too (Tykhonov et al. 2008). The welfare of any firm in a supply chain or supply network directly depends on the performance of the others and their willingness and ability to coordinate (Swaminathan et al. 1994). Managing supply chains or supply networks involves coordination and decision-makings across firms. Information technologies have played a crucial role in managing them more efficiently. Strader et al. (1998) state that "As improvements in information technology have enabled the costs of coordination to decrease, there has been a general movement toward organizing as partnerships between the firms. Supply chain management (SCM) is an important topic to study because it is an instance of these partnerships." The metrics commonly used to measure overall supply chain performance are inventory level and cost. A major impediment to the performance is uncertainty involved in the supply chain and it is the inventory which is often used to protect the supply chain from the uncertainty.

2.13
According to Smith and Davis (1988), "distributed problem solving is the cooperative solution of problems by a decentralized and loosely coupled collection of knowledge sources located in a number of distinct processor nodes." Also, Strader et al. (1998) state "distributed problem solving is often necessary because no one node has sufficient information to solve the entire problem." Following their arguments, a distributed system model may be most appropriate to describe a supply network. A supply network is composed of multiple firms and subject to a dynamic environment. In a constantly changing environment, the firms need to learn and adapt themselves to be able to survive in the long run. However, according to Choi et al. (2001), "the firms' efforts to manage supply networks have often led to frustration and helplessness. Managers have struggled with the dynamic and complex nature of supply networks and the inevitable lack of prediction and control." As an effort to deal with the dynamic and complex nature more effectively, the research community in the field of supply networks has begun adopting the CAS perspective. The article by Choi et al. (2001) is a pioneering research that employed such an approach. However, Pathak et al. (2007) mention that, since the article by Choi et al. (2001), "there have been only a handful of papers that use the CAS view of supply networks, signaling that the SCM discipline has yet to enthusiastically embrace the CAS perspective."

2.14
Therefore, a supply network can be modeled as a complex adaptive system consisting of diverse agents and their interactions, in which macro-level system behaviors can be directly traced to micro-level behavioral decision rules of the autonomous and adaptive agents. The agents are regarded as social agents with many dimensions of social interactions (North et al. 2007). From the modeling and simulation perspective, while traditional operations research methods were useful for simulating hierarchical production systems with the centralized decision-makings, a supply network with its decentralized decision-makings is more appropriately modeled as a social simulation (Strader et al. 1998). Therefore, ABSS is gaining increasing acceptance as a method of modeling and simulating supply networks under the CAS paradigm.

2.15
The followings are examples of research works which have employed agent-based simulations approach for analyzing supply networks and I compare the similarities and the differences between them and this work. Kimbrough et al. (2002) use artificial agents to model the MIT Beer Game, a supply chain simulation game played by human participants. They conclude that the agent-based approach is suitable to apply in modeling the game by showing the agents' capabilities of playing the game effectively and adapting themselves in a changing business environment. I also use the Beer Game as a basic framework of my ABSS model, but extend its original chain structure into a full network structure in which the number of agents and the complexity of their relationships increase much further.

2.16
Strader et al. (1998) implement supply network models in the agent-based simulation platform to study the impact of information sharing on order fulfillment in divergent assembly supply networks. They show that efficient information sharing enables inventory costs to be reduced because of enhanced coordination and reduced uncertainty. Also, North et al. (2007) describe a computational model, called the Value Network Model, which was developed to investigate the costs and consequences of increasing information visibility in supply networks through agent-based simulations. The models in the aforementioned two papers and my model commonly employ agent-based simulation approaches. However, the effects of information sharing on the supply network performance are not analyzed in my work since the main purpose is to analyze decision-making behaviors of firms based on a more realistic assumption of local information availability only, as mentioned before in introduction section.

2.17
Tykhonov et al. (2008) model trust as an individual-level agent's characteristic and evaluate the trust value based on the experiences gained by the agent. Their work and my work both focus on analyzing human behavior through ABSS and deal with trust and governance mechanisms in supply networks. However, the main difference between them is that the individual-level models in Tykhonov et al. (2008) consider three factors of trust, deception, and trade in reproducing agents' decisions and behavior, while my model considers a trust factor only. Also, in the research work of Macal (2004), various social interaction mechanisms, in which trust between agents is an endogenous property of the system, are proposed on the basis of reciprocity relationships, such as "tit-for-tat" (Axelrod 1984). I also develop a framework for modeling trust relationships and apply it to study the impacts of trust relationships on supply network dynamics. In addition, the effects of the agents' decision-making behaviors, reflecting the trust factor, on the performance of inventory management are analyzed in my work. However, unlike Strader et al. (1998) and North et al. (2007), inventory costs incurred in the system are not analyzed, since my model is not a system-wide optimization model geared toward cost minimization, which has been emphasized in the SCM research.

2.18
Akkermans (2001) describes an exploratory study of emerging decentralized supply networks and develops a simulation model in a system dynamics simulation environment using an agent-based approach. Each agent in the supply network holds mental models of the performance of the other agents it is interacting with. Preferences for doing business with these other agents are driven by these mental models. The simulations result shows that stability in this complex network emerges spontaneously as relative preferences for a specific supplier or customer become fixed over time. Taking a similar modeling and simulations approach, Schieritz and Größler (Schieritz 2003) also show that the development of fixed preferences leads to a long-term relationship between a customer and its supplier, thereby resulting in a stable supply network structure. Despite the different simulation methods employed, the basic modeling approaches taken by their works and my work are quite comparable in that they all focus on modeling actual human behavior and try to find emergent outcomes of stable supply network structures.

* Modeling Framework

A supply network model

3.1
For a simulation model, the original "Beer Game" model (Sterman 1989;Sterman et al. 1991;Sterman 1992) is extended into a supply network in this study. The beer game model considers a supply chain with five stages or types of agents: a single customer, retailer, wholesaler, distributor, and factory. The original "Beer Game Simulation" is a systems dynamics simulation model (Forrester 1961) that has been used extensively to study supply chain behavior. However, in this study, an ABSS approach is adopted to develop an extended beer game simulation model, as shown in the next section.

3.2
In the Beer Game, each agent in a supply chain needs the following decision rules: a demand forecasting rule, an ordering rule and a supply rule. Based on these rules, each agent forecasts the expected demand and decides how many items to order and ship in each time period depending on its inventory, outstanding orders in the pipeline[3], and the orders and shipments it has received. The temporal ordering of events in the Beer Game is as follows[4] (Kimbrough et al. 2002):

3.3
Since the linear supply chain is extended, in this study, into a full supply network model in which each stage of the network consists of multiple agents, each agent in a supply network requires the following additional decision rules: order allocation and supply allocation rules. More specifically, each agent, except factory agents, should now decide how much to order as well as how to allocate the order quantity to its upstream agents. Likewise, each agent, except final customer agents, should now decide how much to supply as well as how to allocate the supply quantity to its downstream agents.

3.4
The simulation model presented in this paper employs the same rules used in the original beer game simulations for the basic three rules: a demand forecasting rule, an ordering rule and a supply rule. And for the order allocation and supply allocation rules, which are unique to the supply network, the model considers a social factor, "trust," which depends on the experience of social interaction between agents.

Modeling trust relationships

3.5
According to Tykhonov et al. (2008), the development of trust is contingent on the context in which interaction occurs or on the observer's point of view. Also, Doney and Cannon (1997) state that a collaborative relationship based on mutual trust relies on relational forms of exchange. Therefore, in the supply network context, the specific forms of exchange correspond to ordering and supplying between two firms. Akkermans (2001) provides a conceptual framework that can be adopted for modeling trust relationships in terms of ordering and supplying. He states in the paper that the more a customer orders from a supplier, the heavier the supplier's reliance on this customer will become over time, and hence the greater allocation of his shipments to the customer. Likewise, the more shipments a customer receives, the more he will start to appreciate this supplier. As a matter of fact, Macal (2004) employs a similar framework and assigns a trust measure as a result of the interaction between two agents, consisting of ordering and supplying. He defines trust measures in terms of order quantities and shipment quantities. Tykhonov et al. (2008) model trust as an individual-level agent's characteristic and develops an asymmetric trust update function in which the trust level is updated based on the agent's experience of trading, which may be either positive or negative experience according to the classification of Jonker and Treur (1999). Based on the conceptual frameworks presented in the aforementioned papers, trust relationships in this study are modeled as follows.

3.6
In a supply network, an interaction between a pair of upstream agent and downstream agent consists of an action by one agent and a reaction by the other agent, both of which correspond to variables of non-negative real numbers in this model. Generally, participants in a relationship desire reciprocity, by which one is morally obligated to give something in return for something received or one expects to receive something in return for something given (Gouldner 1959). Therefore, the concept of reciprocity is reflected in the model as follows. From a downstream agent's point of view, an action is the amount it orders from an upstream agent, and a reaction is the amount the upstream agent supplies to the downstream agent in response to that order. Likewise, from an upstream agent's point of view, an action is the amount it supplies to a downstream agent, and a reaction is the amount the downstream agent orders from the upstream agent in response to that supply. Associated with the trust update, the experience based on the interaction between two agents can be either positive or negative. A positive experience, which increases trust, is defined as one in which reaction ≥ action, while a negative experience, which decreases trust, is defined as one in which reaction < action. Therefore, the experience continuously increases or decreases the level of trust in the partner agent.

3.7
To be more specific, from a downstream agent's point of view, if the latest shipment received corresponding to its previous order meets or exceeds[6] that order, the downstream agent's trust in the upstream agent increases, and if not, its trust in the upstream agent decreases. In updating its trust in the upstream agent, the downstream agent reflects its current experience as well as its past experiences with the upstream agent. Mathematically, it adaptively updates its trust value through a convex combination of the trust value of current period and that of last period. This means that trust is a cumulative product of repeated past interactions (Ring and Van de Ven 1994). Here it is assumed that the downstream agent conservatively updates its trust value by taking the trust value of current period as the minimum value of action and reaction. That is, in the case of positive experience, in which reaction ≥ action, the current trust value is set equal to the value of the initiating action which corresponds to the order. And in the case of negative experience, in which reaction < action, the current trust value is set equal to the value of the resulting action which corresponds to the supply.

3.8
Now let ρ be the adaptation parameter which has a value in (0,1). And it is assumed that there is a delay time between an action and the associated reaction. Let o and s represent ordering delay and shipping delay, respectively. Then, in a pair of a downstream agent k and an upstream agent j, the downstream agent k 's trust in the upstream agent j at time tm (where m = 1, 2, 3, ...) is modeled as follows:
Positive experience: Shipmentjk,tm-s ≥ Order kj, tm-s-o

Trust kj, tm = MAX[Trust kj, t m-1, ρ Orderkj, tm-s-o + (1- ρ) Trust kj, t m-1] (3.1)

Negative experience: Shipmentjk, tm-s < Orderkj, tm-s-o

Trust kj, tm = MIN[Trust kj, t m-1, ρ Shipmentjk, tm-s + (1- ρ) Trust kj, t m-1] (3.2)

where MAX and MIN functions are used for the self-reinforcing mechanism which induces positive feedbacks. That is, in the case of positive experience, the trust value never goes down, and in the case of negative experience, the trust value never goes up. Moreover, this self-reinforcing mechanism corresponds to an argument by Ring and Van de Ven (1994) that the more frequently the parties have successfully transacted, the more likely they will bring higher levels of trust to subsequent transactions.

3.9
Likewise, from an upstream agent's point of view, if the latest order received meets or exceeds the previous shipment, the upstream agent's trust in the downstream agent increases, and if not, its trust in the downstream agent decreases. With the same approach mentioned above, in a pair of an upstream agent k and a downstream agent i, the upstream agent k 's trust in the downstream agent i at time tm is modeled as follows:
Positive experience: Orderik, tm-o ≥ Shipmentki, tm-s-o

Trust ki, tm = MAX[Trust ki, t m-1, ρ Shipmentki, tm-s-o + (1- ρ) Trust ki, t m-1] (3.3)

Negative experience: Orderik, tm-o < Shipmentki, tm-s-o

Trust ki, tm = MIN[Trust ki, t m-1, ρ Orderik, tm-o + (1- ρ) Trust ki, t m-1] (3.4)

The equations of (3.1), (3.2), (3.3) and (3.4) show that within each pair of agents, trust levels may differ, implying the possibility of asymmetrical trust relationships

Behavioral decision rules: supply and order allocation decisions

3.10
Schieritz and Größler (2003) and Macal (2004) suggest several evaluation criteria that can be used as the basis for allocating total supply and total order to the corresponding agents, respectively. The criteria include factors associated with the past experience of interaction between agents, such as the volume exchanged, the frequency of exchanges and the degree of relationship that has been built upon, and those associated with the current status of partner agents, such as the number of unmet orders to fulfill (backorders) and the ability to fulfill current orders. The simulation studies in this paper compare and then combine two heuristic methods regarding each agent's behavioral decision-makings on the supply and the order allocations: backorder-based heuristics and trust-based heuristics. Each agent makes the supply and the order allocation decisions based on locally available information only as well as using a heuristic method of choice.

3.11
In the backorder-based heuristic algorithms, which have been widely used in the industry as a standard allocation heuristics, an agent considers the backorder status of the associated agents in the allocation decisions. More specifically, for the supply allocation decisions, so-called LBF (Largest Backorder First) scheme is applied. With this scheme, an agent prioritizes its immediate downstream agents on the basis of larger backorder and the total supply is allocated in proportion to their existing backorders it has to meet, meaning that the larger the backorder, the larger the amount to be supplied. And for the order allocation decisions, so-called SBF (Smallest Backorder First) scheme is applied. With this scheme, an agent prioritizes its immediate upstream agents on the basis of smaller backorder and the total order is allocated in inverse proportion to its existing backorders on them, meaning that the larger the backorder, the smaller the order. Mathematically, given an agent k 's total supply and total order at time tm, denoted by Total_Shipment k,tm and Total_Order k,tm, respectively, the agent k allocates the total supply to a downstream agent i and the total order to an upstream agent j as follows:
Supply Allocation Rule:

Shipment ki,tm = Total_Shipment k,tm * [ Backorder ki,tm / ∑ i Backorder ki,tm ] (3.5)

Order Allocation Rule:

Order kj ,tm = Total_Order k,tm * [ (1/Backorder jk,tm) / ∑ j (1/Backorder jk,tm) ] (3.6)

3.12
Similarly, in the trust-based heuristic algorithms, an agent considers its trust levels for the associated agents in the allocation decisions. More specifically, for both the supply allocation and the order allocation decisions, an agent prioritizes the associated agents on the basis of larger trust level, and the total supply and the total order are allocated in proportion to its current trust levels for them. Associated with the order allocation decision, this means that as the level of trust increases, greater reliance may be placed on the trusted party (Ring and Van de Ven 1992). Also, associated with the supply allocation decision, it corresponds to the argument of Akkermans (Akkermans 2001) that the more an agent orders from the other agent, the heavier the other agent's reliance on the agent will become over time, and hence the greater his allocation of shipments to the agent. The similar argument may be true for the case of order allocation as well. Mathematically, given an agent k 's total supply and total order at time tm, the agent k allocates the total supply to a downstream agent i and the total order to an upstream agent j as follows:
Supply Allocation Rule:

Shipment ki,tm = Total_Shipment k,tm * [ Trust ki,tm / ∑ i Trust ki,tm] (3.7)

Order Allocation Rule:

Order kj,tm = Total_Order k,tm * [ Trust kj,tm / ∑ j Trust kj,tm ] (3.8)

3.13
Now to analyze the effects of the trust mechanism on the performance of complex adaptive supply networks, the simulation studies in this paper also consider the following algorithms combining both backorder-based heuristics and trust-based heuristics:
Supply Allocation Rule:

Shipment ki,tm = Total_Shipment k,tm * [(1-γ)Backorder ki,tm+γTrust ki,tm] / [(1-γ)∑ i Backorder ki,tm+γ∑ i Trust ki,tm] (3.9)

Order Allocation Rule:

Order kj,tm = Total_Order k,tm * [(1-γ)(1/Backorder jk,tm)+γTrust kj,tm] / [(1-γ)∑ j (1/Backorder jk,tm)+γ∑ j Trust kj,tm] (3.10)

where γ has a value in (0,1) and represents the relative weight on the trust level compared to the backorder level in the above allocation decisions.

* Simulations

Simulation model

Figure
Figure 1. A supply network with L=5 and N=3

4.1
Let L denote the number of stages in the supply network and N denote the number of agents in each stage. For simulations, a supply network with L=5 and N=3, therefore a total of 15 agents, is considered as shown in Figure 1. The simulation models in this paper implement heterogeneous agents[7] who are different only in terms of their initial inventory levels. More specifically, the agents located in the first column in Figure 1 initially hold the most inventory levels, while those in the third column initially hold the least inventory levels. Therefore, as Schieritz and Größler (2003) imply, even though all agents in the same stage employ the same decision-making rules, they will all show different evolutionary paths in terms of the volume exchanged over the course of the simulation.

4.2
Besides the parameters mentioned before, that is, ρ (the adaptation parameter for updating the current trust level) and γ(the relative weight on the trust level compared to the backorder level in the allocation decisions), the additional parameters necessary for the simulations are adopted from the original beer game simulation model in Sterman (1989) and Sterman et al. (1991). Regarding the ordering rule in the model, each agent forecasts the expected demand from its immediate downstream agent and decides how many items to order in each time period on the basis of its actual and desired inventory levels, actual and desired outstanding orders in the pipeline, and the orders and shipments it has received. Using the parameters adopted from the beer game model, an agent k 's total order, given the expected demands from its downstream agent i 's, at time tm can be mathematically represented as follows:

Total_Order k,tm = ∑iExpected_Demand ik,tm + Stock_Adjustment k,tm + Pipeline_Adjustment k,tm
= θ ∑ i Order ik,t m-1 + (1- θ) ∑ i Expected_Demand ik,t m-1 + aS (Desired_Inventoryk - Inventory k,tm) + aPL (Desired_Pipelinek - Pipeline k,tm)
= θ ∑ i Order ik,t m-1 + (1- θ) ∑ i Expected_Demand ik,t m-1 + aS (Qk - Inventory k,tm -βPipeline k,tm) (4.1)

where θ : adaptation parameter controlling the rate at which demand expectations are updated aS : stock adjustment parameter (fraction of the discrepancy between the desired and the actual inventory) (=α) aPL: pipeline adjustment parameter (fraction of the discrepancy between the desired and the actual pipeline) β= aPL/aS & Qk = Desired_Inventoryk + β Desired_Pipelinek

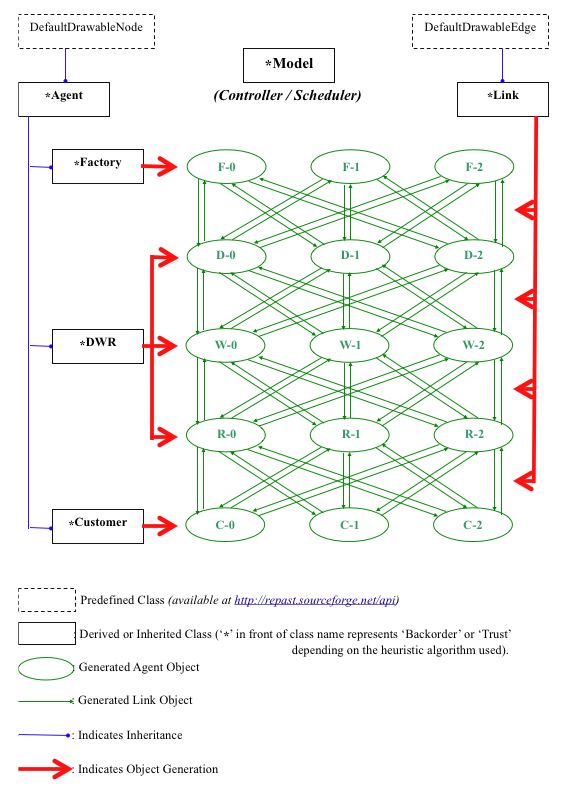
Figure
Figure 2. The simulation model structure with a case of L=5 and N=3

4.3
In the simulations, each customer's demand ramps up from 4 to 8 at time t4 and stays at the same level thereafter as in the original beer game simulation. This steep increase of demand induces unstable system behaviors[8]. This prevents the whole system from entering into a stable mode of equilibrium state during the early simulation time periods. Also as in the original beer game simulation, a one-period ordering delay, a two-period shipping delay and a three-period production delay in simulation time are assumed. Initially at t1, there are 8 items in the pipeline of each agent, of which 4 items will be delivered to its warehouse at t2and the other 4 items will be delivered to its warehouse at t3 (Kimbrough et al. 2002). The initial inventory levels of the agents, exclusive of customer agents, located in the first, second and third columns in Figure 1 are assumed to be 40, 20 and 0, respectively.

4.4
The simulation model structure with a case of L=5 and N=3 is shown in Figure. 2. The outlines of the algorithms for the 6 classes (*Model, *Link, *Agent, *Factory, *DWR, *Customer) in Figure. 2 are provided in the Appendix.

Analyses of simulations results

Figure
Figure 3. A simulation output with the backorder-based heuristic algorithms

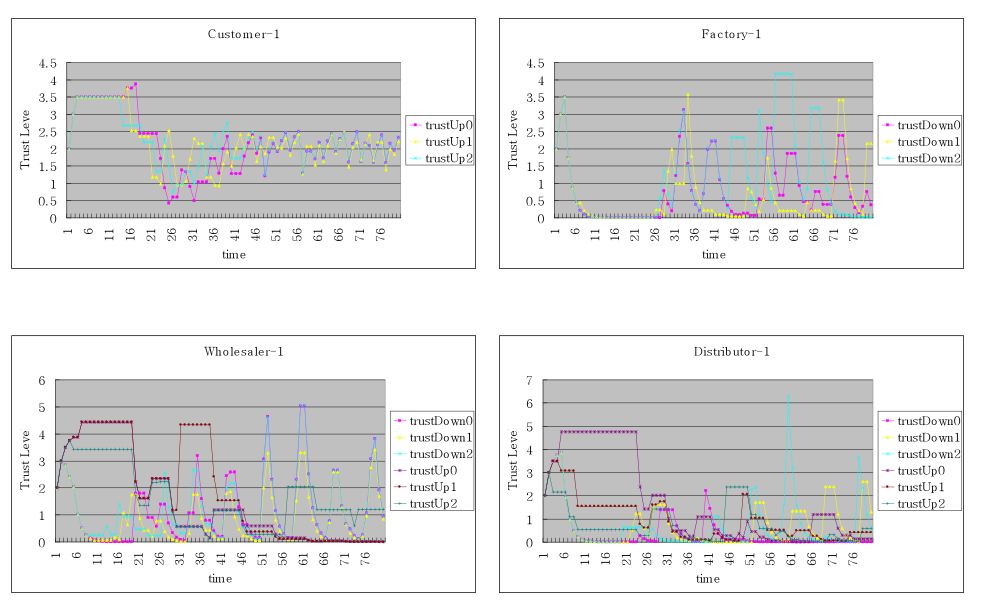
Figure
Figure 4. Trust levels of 4 sample agents with the backorder-based heuristic algorithms

Figure
Figure 5. A simulation output with the trust-based heuristic algorithms

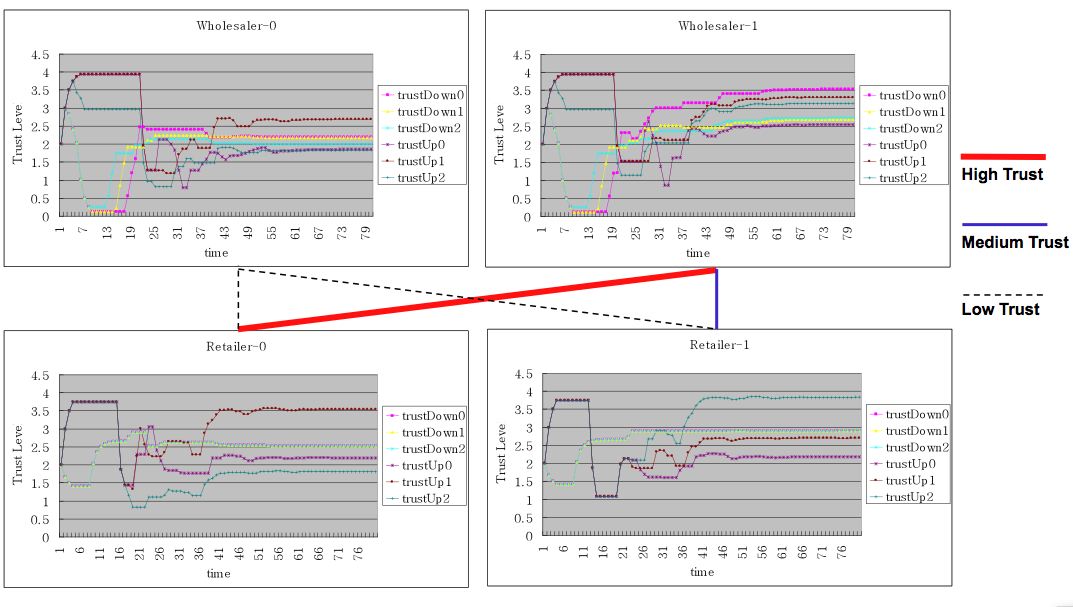
Figure
Figure 6. Trust levels of 4 neighboring agents and their trust relationships with the trust-based heuristic algorithms

4.5
Figure 3 shows a snapshot of a Java-based Repast program running on the Eclipse environment[9]. The program implements the backorder-based heuristic algorithms with the parameter values shown in the snapshot and shows a graph of inventory level vs. time[10]. The graph shows that the inventory levels of all agents in the supply network, exclusive of customer agents, keep fluctuating continuously.

4.6
The trust levels of all agents are also estimated with the backorder-based heuristic algorithms. Figure 4 shows 4 sample graphs of trust level vs. time in which trustUp denotes an agent's trust level for its upstream agent and trustDown denotes an agent's trust level for its downstream agent. For example in the graph, from a Distributor-1's point of view, trustUp0, trustUp1 and trustUp2 denote its trust levels for Factory-0, Factory-1 and Factory-2, respectively, and trustDown0, trustDown1 and trustDown2 denote its trust levels for Wholesaler-0, Wholesaler-1 and Wholesaler-2, respectively. Figure 4 shows that the agents' trust levels for their associated agents in the supply network keep fluctuating continuously. In fact, the same is true even for all other agents that are not shown in Figure 4.

4.7
Figure 5 shows a simulation output for the trust-based heuristic algorithms with the same parameter values used in the case of backorder-based heuristic algorithms. The graph in Figure 5 shows that the inventory levels of all agents in the supply network, exclusive of customer agents, are initially fluctuating, but eventually stabilizing into an equilibrium state.

4.8
The trust levels of all agents are also estimated with the trust-based heuristic algorithms. Figure 6 shows the trust levels of some 4 neighboring agents as well as their trust relationships. The trust levels of all agents in Figure 6 are initially fluctuating, but eventually stabilizing into an equilibrium state, which represents the process of building their trust relationships (Dwyer et al. 1987). That is, the periods of fluctuation represent transient times for probing and evaluating the trustworthiness among agents and show unsymmetrical trust levels between any two partner agents. The following periods of stabilization show that as the partner agents finalize their levels of trust for each other, the trust levels between the two become symmetrical[11]. Ultimately, through the same process, the degree of trust relationship in each pair of partner agents emerges. These results appear to fit well with the findings from Akkermans (2001) and Schieritz and Größler (2003) that although individual preferences continue to fluctuate, relatively soon the preferences become locked in or remain constant and, from there on, the agents become long-term partners in a stable network[12].

4.9
As a matter of fact, the work of Akkermans (2001) shows a real-world case of situations which correspond to the findings in this work. In the supply network ASML, a manufacturer of state-of-the-art lithographic equipment, i.e. the machines that manufacture wafers of integrated circuits (ICs), there has been a considerable emphasis on developing long-term relationships with key suppliers. Mutual trust plays an important part in their management policy and trust has been severely tested in the past due to the steep ramp-ups and ramp-downs that characterize the lithography industry. Suppliers are surprised by sudden decreases in ASML's orders when the IC business cycle turns downward and face considerable supply chain difficulties. As a result, some suppliers are reluctant to trust a steep increase in orders as the business cycle turns up again. Despite ASML's emphasis on long-term relationships with suppliers, it is with these skeptical suppliers that the company's level of business decreases over time. As a result, many of ASML's key suppliers are the same ones that the company started off with over fifteen years ago. According to Akkermans (2001), the results of the lock-in are consistent with findings from complexity theory and economics regarding lock-in and path dependence. The resulting degrees of trust relationships among the 4 agents are denoted by the differentiated lines in Figure 6, namely, thick line, thin line and dashed line representing high degree, medium degree and low degree trust relationships, respectively.

Figure
Figure 7. The emergent structure of collaboration patterns with the trust-based heuristic algorithms

4.10
In fact, similar patterns can be found for the trust relationships among all other agents in the supply network, and the resulting emergent structure of collaboration patterns, including the outcomes of Figure 6 in part, is shown in Figure 7. This result coincides with the outcomes of Akkermans (2001), Schieritz and Größler (2003) and Macal (2004) in that despite the independent nature of the agents, stability in the complex network emerges and finally an emergent supply network is derived. A dominated agent, denoted by the dashed rectangle in Figure 7, is the one who could not establish a strong collaborative relationship based on high trust level with at least one of its upstream or downstream agents. This does not necessarily mean that the dominated agent is not able to trade at all with any of its upstream or downstream agents. However, its trading amounts with them are relatively small. In Figure 7, Factory-2, Distributor-0 and Wholesaler-0 are dominated agents who are not at all connected by a thick line which represents a high degree trust relationship.

4.11
One thing to note in the collaboration patterns in Figure 7 is that an agent who has a strong collaborative relationship with at least one of its upstream agents also has a strong collaborative relationship with at least one of its downstream agents. Likewise, an agent who has a strong collaborative relationship with at least one of its downstream agents also has a strong collaborative relationship with at least one of its upstream agents. These findings imply transitions of trust relationships. To provide a clearer understanding of these findings, let's consider an example with three agents A, B and C and assume that A is B's upstream agent and C is B's downstream agent. Given these, an agent B's strong collaborative relationship with its upstream agent A almost guarantees stable supplies to agent B, which in turn almost guarantees stable supplies to its downstream agent C. Hence a strong collaborative relationship between B and its upstream agent A leads to a strong collaborative relationship between B and its downstream agent C. Likewise, agent B's strong collaborative relationship with its downstream agent C almost guarantees stable demands towards agent B, which in turn almost guarantees stable demands towards its upstream agent A. Therefore a strong collaborative relationship between B and its downstream agent C reinforces a strong collaborative relationship between B and its upstream agent A as well. These transitions of strong or weak trust relationships ultimately result in dominant or dominated agents.

Figure
Figure 8. Inventory levels of all agents with the combined algorithms and γ = 0.2

Figure
Figure 9. Inventory levels of all agents with the combined algorithms and γ = 0.5

Figure
Figure 10. Inventory levels of all agents with the combined algorithms and γ = 0.8

4.12
To analyze the effects of the trust mechanism on the inventory levels of all agents, simulations were run with the combined algorithms shown in equations (3.9) and (3.10). The model has been tested for sensitivity to changes in parameter _ with respect to inventory levels. The graphs in Figure 8, 9 and 10 show inventory levels vs. time with γ = 0.2, 0.5 and 0.8, respectively. The three graphs are almost the same in the early time periods, regardless of the γ values. However, after the periods, as the value of γ becomes larger, the variability of inventory levels becomes smaller, and with some large values of γ, inventory levels are almost stabilizing. To see these phenomena better, the inventory levels of Distributor agents are picked out from Figure 8, 9 and 10 and separately shown in Figure 11, 12 and 13. All these results imply that as agents rely more on trust as a factor in the supply and the order allocation decisions, the variability of inventory levels becomes smaller, which ultimately improves the performance of inventory management, a crucial factor of SCM performance.

Figure
Figure 11. Inventory levels of Distributors with the combined algorithms and γ = 0.2

Figure
Figure 12. Inventory levels of Distributors with the combined algorithms and γ = 0.5

Figure
Figure 13. Inventory levels of Distributors with the combined algorithms and γ = 0.8

* Implications and Future Research

5.1
This paper modeled a supply network as a complex adaptive system, in which agents interact with one another and adapt themselves. It also conducted agent-based simulations, a research method for complex adaptive systems, to observe emergent outcomes. For the simulation model, the original Beer Game is used as a basic framework. The original Beer Game is a classic case of a multi-tiered supply chain model that has been used extensively to study supply chain behavior. Although simplified when compared to the complexities of real-world supply chains, it nevertheless exhibits important properties of real-world supply chains (Macal 2004). To add realism in the supply chain dynamics, I extended its original chain structure into a full network structure in which the number of agents and the complexity of their relationships increase much further.

5.2
From the perspective of complex systems theory, the collaboration patterns in the supply network shown in Figure 6 are an emergence resulting from the self-organizing process of the relevant agents. That is, the agents interact with one another based on their own behavioral decision-making rules and adapt themselves through the self-organizing process, which eventually derives macro patterns. The self-organizing process also results in symmetrical trust levels in each pair of trading agents as well as transitions of trust relationships as explained in the previous section. After all, trust plays a critical role in stabilizing the constituent links of a supply network and developing long-term relationships among its constituent agents, thereby decreasing transaction costs through mutual learning and other forms of coevolving (Doney and Cannon 1997;Akkermans 2001;Tykhonov et al. 2008).

5.3
Another interesting outcome in the simulations is that the variability of inventory levels becomes smaller as agents rely more on trust as a factor in the supply and the order allocation decisions. This result can be explained by the fact that uncertainty of an agent about the partner agent's trustworthiness can be diminished based on their past experiences of trading. That is, mutual trust relationship based on the past experiences of trading diminishes an agent's uncertainties about trustworthiness of its trading partners and thereby tends to stabilize its inventory level. This result implies that even without explicit information sharing among agents in a supply chain or a supply network, which has proven to be a very effective solution to improve the performance of inventory management in the SCM researches (e.g.Strader et al. 1998;Angulo et al. 2004;North et al. 2007), agents' decision-making behavior based on the trust relationship can somewhat contribute to the reduction in the variability of inventory levels. Given that information sharing among firms in a supply chain or a supply network has not been executed well in reality (Madlberger 2008), agents' decision-making behavior based on the trust relationship may be a more realistic solution in stabilizing inventory levels. However, this assertion needs to be backed up by relevant empirical studies as well, which can lead to a follow-up research.

5.4
The simulation models in this paper implemented heterogeneous agents who are different only in terms of their initial inventory levels. In future research, more variety of agents' decision-making rules and attributes such as degree of rationality, risk attitude, and so on could be accommodated with regard to the agents' heterogeneity. Also in this paper, the concept of trust is mathematically modeled only based on the interaction of ordering and supplying decisions. In future research, it needs to be extended in a more realistic way so that it reflects qualitative factors such as quality of goods in trade, firm's reputation and integrity, and so on.

* Appendix: The Outlines of the Algorithms for the 6 Classes in Figure 2

*Model class (controller / scheduler)
  1. Create total L x N array variables of the * Agent class type, agent [0][0]~ agent [L-1][N-1], for a supply network with L stages and N agents in each stage.
  2. Generate N agents from each of the classes, * Customer and * Factory, and (L-2) x N agents from the class, * DWR. Label each agent's name appropriately as shown in Fig. 2.
  3. Allocate each agent to the corresponding array variable created in step 1, with the parameter values of α, β, θ, ρ, γ and initial inventory level.
  4. Generate total 2 x (L-1) x N2 links from the * Link class.
  5. Connect between each pair of two agents using two links generated in step 4, but with opposite directions (one for ordering and the other for supplying) as shown in Fig. 2.
  6. Build the simulation schedules as follows: 
    For  tm =  t1 to tT,  // T is total simulation time steps.
  For i=0 to L-1,
    For j=0 to N-1,
       Call  agent [i][j]. step(tm);	// Execute each agent's  step()method.
*Link class
  1. Create 2 reference variables of the LinkedList class type: queue for storing the current order or shipment information and record for recording the past order or shipment information.
  2. Define the following methods which are needed by the agents during their interactions of trading:
*Agent class
Define the following methods which are needed by the agents during their interactions of trading:
*Factory class
Create a reference variable of the LinkedList class type, prod_line for implementing production delay, and define step() method which executes the followings for each agent generated from this class:
  1. Receive an order from each of its N downstream agents by calling the method order_in()defined in the *Agent class.
  2. Retrieve a past shipment delivered to each of its N downstream agents by calling the method past_shipment() defined in the *Agent class.
  3. For each of its N downstream agents, compare the associated values obtained in step 1 and step 2, and determine its trust level for the downstream agent based on eqs. (3.1) and (3.2).
  4. Receive items from the production line by retrieving a value in the head of the linked list, prod_line, and deleting it.
  5. Determine the amount of supply for each of its N downstream agents, as either its unmet orders to fulfill toward the downstream agent or available items in stock allocated to the agent, whichever is less. The allocation will be based on one of the following supply allocation rules:
  6. Eq. (3.5) when using backorder-based heuristic algorithms
  7. Eq. (3.7) when using trust-based heuristic algorithms
  8. Eq. (3.9) when using combined algorithms
  9. Send out each shipment, determined in step 5, to the corresponding downstream agent by calling the method shipment_out() and record it by calling the method current_shipment() defined in the *Agent class.
  10. Update its inventory level as well as all of its pipelines and backorders.
  11. Using parameters θ, α and β, compute the expected demand from each of its N downstream agents, as well as the total demand based on eq. (4.1).
  12. Put the total amount of demand into production by inserting the value to the end of the linked list, prod line.
*DWR class
Define step()method which executes the followings for each agent generated from this class:
  1. Receive a shipment from each of its N upstream agents by calling the method shipment_in() defined in the *Agent class.
  2. Retrieve a past order placed toward each of its N upstream agents by calling the method past_order()defined in the *Agent class.
  3. For each of its N upstream agents, compare the associated values obtained in step 1 and step 2, and determine its trust level for the upstream agent based on eqs. (3.1) and (3.2).
  4. Receive an order from each of its N downstream agents by calling the method order_in() defined in the *Agent class.
  5. Retrieve a past shipment delivered to each of its N downstream agents by calling the method past_shipment() defined in the *Agent class.
  6. For each of its N downstream agents, compare the associated values obtained in step 4 and step 5, and determine its trust level for the downstream agent based on eqs. (3.1) and (3.2).
  7. Determine the amount of supply for each of its N downstream agents, as either its unmet orders to fulfill toward the downstream agent or available items in stock allocated to the agent, whichever is less. The allocation will be based on one of the following supply allocation rules:
    • Eq. (3.5) when using backorder-based heuristic algorithms
    • Eq. (3.7) when using trust-based heuristic algorithms
    • Eq. (3.9) when using combined algorithms
  8. Send out each shipment, determined in step 7, to the corresponding downstream agent by calling the method shipment_out() and record it by calling the method current_shipment() defined in the *Agent class.
  9. Update its inventory level as well as all of its pipelines and backorders.
  10. Using parameters θ, α and β, compute the expected demand from each of its N downstream agents, as well as the total order based on eq. (4.1).
  11. Determine the amount of order to be placed toward each of its N upstream agents by allocating the total order, obtained in step 10, based on one of the following order allocation rules:
    • Eq. (3.6) when using backorder-based heuristic algorithms
    • Eq. (3.8) when using trust-based heuristic algorithms
    • Eq. (3.10) when using combined algorithms
  12. Send out each order, determined in step 11, to the corresponding upstream agent by calling the method order_out() and record it by calling the method current_order() defined in the *Agent class.
*Customer class
Define step() method which executes the followings for each agent generated from this class:
  1. Receive a shipment from each of its N upstream agents by calling the method shipment_in() defined in the *Agent class.
  2. Retrieve a past order placed toward each of its N upstream agents by calling the method past_order() defined in the *Agent class.
  3. For each of its N upstream agents, compare the associated values obtained in step 1 and step 2, and determine its trust level for the upstream agent based on eqs. (3.1) and (3.2).
  4. Total order is set to 4 when the simulation time t <= 4, and 8 when t > 4.
  5. Determine the amount of order to be placed toward each of its N upstream agents by allocating the total order based on one of the following order allocation rules:
    • Eq. (3.6) when using backorder-based heuristic algorithms
    • Eq. (3.8) when using trust-based heuristic algorithms
    • Eq. (3.10) when using combined algorithms
  6. Send out each order, determined in step 5, to the corresponding upstream agent by calling the method order_out()and record it by calling the method current_order() defined in the *Agent class.

* Acknowledgements

This work was supported by the Korea Research Foundation Grant funded by the Korean Government (MOEHRD, Basic Research Promotion Fund) (KRF-2006-321-B00359).

* Notes

1 A 'normative' model describes how decisions should be made, while a 'descriptive' model describes how decisions are being made.

2 Multi-Agent Simulation (MAS) is a simulation method similar to ABSS. MAS is a well-established research and applied branch of Artificial Intelligence (AI). Since MAS is more related with AI, logic-based and cognitive science, it can be defined as the study of societies of autonomous “artificial agents.” In contrast, ABSS can be defined as the study of “artificial societies” of autonomous agents (Conte et al. 1998).

3 The pipeline consists of orders placed but not received.

4 The sequence of supply chain stages from factory to final customer is termed “downstream,” and the sequence of supply chain stages from final customer to factory is termed “upstream.”

5 Backorders, also called backlog of orders, refer to previously unmet demands.

6 The shipment can exceed the order due to the previously unmet demand which is called backorder.

7 The homogeneous agents in the simulation model will produce symmetric simulation results, from which some valuable insights may not be gained.

8 The steep ramp-up is comparable to that used in the simulation experiments of Akkermans (2001) in which business cycles are introduced and a supply network model is tested under severe stress.

9 Eclipse is an open source community whose projects are focused on building an open development platform comprised of extensible frameworks, tools and runtimes for building, deploying and managing software across the lifecycle ( source: http://www.eclipse.org). It provides a Java IDE (Integrated Development Environment) including convenient user interface and other useful tools.

10 The simulations were run for 500 time periods ( t1 ~ t500), but the graph shows the simulation results only up to 80 time periods ( t80). Even after that time, the inventory levels repeat the same pattern, so I chose to show the results only up to that time.

11 The simulation results of symmetrical trust levels coincide with the argument by Anderson and Weitz (1992) that the trust levels in the mutual relationship become symmetrical in the long run, through repeated cyclical interactions between two firms.

12 The argument assumes that preference in their models corresponds to trust in my model.

* References

ABDUL-RAHMAN, A and Hailes, S (2000), Supporting trust in virtual communities. Proceedings of the 33rd Hawaii International Conference on System Sciences, January 1-4, Los Alamitos, CA, pp. 1769-1777.

AKKERMANS, H (2001), Emergent Supply Networks: Simulation of Adaptive Supply Agents. Proceedings of the 34th Hawaii International Conference on System Sciences, January 3-6, Maui, HI, 11 pp.

ANDERSON, J C and Narus, J A (1990), A Model of Distribution Firm and Manufacturing Firm Working Partnership. Journal of Marketing, 54(1), pp. 42-58.

ANDERSON, E and Weitz, B (1989), Determinants of continuity in conventional industrial channel dyads. Marketing Science, 8(4), pp. 310-323.

ANDERSON, E and Weitz, B (1992), The use of pledges to build and sustain commitment in distribution channels. Journal of Marketing Research, 29, February 1992, pp. 18-34.

ANGULO, A, Nachtmann, H and Waller, M A (2004), Supply Chain Information Sharing in a Vendor Managed Inventory Partnership. Journal of Business Logistics, 25(1), pp. 101-120.

AXELROD, R (1984). The Evolution of Cooperation. Basic Books, New York (NY).

CHOI, T, Dooley, K and Rungtusanatham, M (2001). Supply Networks and Complex Adaptive Systems: Control versus Emergence. Journal of Operation Management 19, pp. 351-366.

CONTE, R, Gilbert, N and Sichman, J (1998), MAS and Social Simulation: A Suitable Commitment. Lecture Notes in Computer Science, 1534, pp. 1-9.

DAVIDSSON, P (2002), Agent Based Social Simulation: A Computer Science View. Journal of Artificial Societies and Social Simulation 5(1) 7 https://www.jasss.org/5/1/7.html.

DONEY, P M and Cannon, J P (1997), An examination of the nature of trust in buyer-seller relationships. Journal of Marketing, 61, April 1997, pp. 35-51.

DWYER, R, Schurr, P and Oh, S (1987), Developing buyer-seller relationships. Journal of Marketing, 51, April 1987, pp. 11-27.

FORRESTER, J W (1961), Industrial Dynamics. MIT Press, Cambridge, MA.

GOULDNER, A (1959), Reciprocity and autonomy in functional theory. Symposium on Sociological Theory, Harper and Row, New York, pp. 241-280.

HART, P and Saunders, C (1997), Power and trust: Critical factors in the adoption and use of electronic data interchange. Organization Science, 8(1)), pp. 23-42.

HOLLAND, J H (1995), Hidden Order. Addison-Wesley, Reading, MA.

IACOBUCCI, D and Hibbard, J D (1999), Toward an encompassing theory of business marketing relationships and interpersonal commercial relationships. Journal of Interactive Marketing, 13, Summer, pp. 13-33.

ISHAYA, T and Macaulay, L (1999), The role of trust in virtual teams. Electronic Journal of Organizational Virtualness, 11(1), pp. 140-157.

JARVENPAA, S L, Knoll, K and Leidner, D (1998), Is anybody out there? The antecedents of trust in global virtual teams. Journal of Management Information Systems, 14(4), pp. 29-64.

JONKER, C M and Treur, J (1999), Formal analysis of models for the dynamics of trust based on experiences, Proceedings of MAAMAW'99, LNAI 1647, pp. 221-232.

KIMBROUGH, S O, Wu, D J and Fang, Z (2002), Computers play the beer game: can artificial agents manage supply chains?. Decision Support Systems, 33(3), pp.323-333.

LIN, F, Sung, Y and Lo, Y (2005), Effects of trust mechanisms on supply-chain performance, International Journal of Electronic Commerce, 9(4), pp. 91-112.

LIN, H M (2006), Interorganizational Collaboration, Social Embeddedness, and Value Creation: A Theoretical Analysis. International Journal of Management, 23(3), pp. 548-558.

MACAL, C M (2004), Emergent structures from trust relationships in supply chains, Proceedings of Agent 2004 Conference, October 7-9, Chicago, IL, pp. 743-760.

MADLBERGER, M (2008), International collaboration in supply chain management. Proceedings of the 41st Hawaii International Conference on System Sciences, January 7-10, Walkoloa, HI, 11 pp.

MAYER, R C, Davis, J H and Schoorman, F D (1995), An integrative model of organizational trust. Academy of Management Review, 20(3), pp. 709-734.

MORGAN, R M and Hunt, S D (1994), The Commitment-Trust Theory of Relationship Marketing. Journal of Marketing, 58, July 1994, pp. 20-38.

NORTH, M J and Macal, C M (2007), Managing Business Complexity: Discovering Strategic Solutions with Agent-Based Modeling and Simulation, Oxford University Press, New York.

PARUNAK, H V D, Savit, R and Riolo, R L (1998), Agent-Based Modeling vs. Equation-Based Modeling: A Case Study and Users' Guide. Multi-Agent Systems and Agent-Based Simulation, Springer Verlag.

PATHAK, S, Day, J, Nair, A, Sawaya, W and Kristal, M (2007), Complexity and Adaptivity in Supply Networks: Building Supply Network Theory Using a Complex Adaptive Systems Perspective. Decision Science, 38(4), pp. 547-580.

RING, P S and Van de Ven, A (1992), Structuring cooperative relationships between organization. Strategic Management Journal, 13, pp. 483-498.

RING, P S and Van de Ven, A (1994), Developmental processes of cooperative interorganizational relationships. Academy of Management Review, 19(1), pp. 90-118.

SALLACH, D and Macal, C M (2001), The simulation of social agents: an introduction. Special Issue of Social Science Computer Review, 19(3), pp. 245-248.

SAMUELSON, D A and Macal, C M (2006), Agent-Based Simulation Comes of Age: Software opens up many new areas of application, OR/MS Today, 33(4), August.

SCHIERITZ, N and Größler, A (2003), Emergent Structures in Supply Chains: A Study Integrating Agent-Based and System Dynamics Modeling. Proceedings of the 36th Hawaii International Conference on System Sciences, January 6-9, Big Island, HI, 9 pp.

SMITH, R G and Davis, R (1988), Frameworks for Cooperation in Distributed Problem Solving. Distributed Artificial Intelligence, Morgan Kaufmann Publishers, San Mateo, CA.

STERMAN, J (1989), Modeling managerial behavior: misperceptions of feedback in a dynamic decision making experiment. Management Science, 35(3), pp. 321-339.

STERMAN, J, Mosekilde, E and Larsen, R (1991), Coping with complexity: Deterministic chaos in human decision making behavior. Beyond Belief: Randomness, Prediction, and Explanation in Science, CRC Press, Boston, pp. 199-229.

STERMAN, J (1992), Teaching takes off: flight simulators for management education -The Beer Game. ORMS Today, 20(5), pp. 40-44.

STRADER, T J, Lin, F and Shaw, M J (1998), Simulation of Order Fulfillment in Divergent Assembly Supply Chains. Journal of Artificial Societies and Social Simulation 1(2) 5 https://www.jasss.org/1/2/5.html.

SWAMINATHAN, J M, Smith, S F and Sadeh, N M (1994), Modeling the Dynamics of Supply Chains. The Robotics Institute, Carnegie Mellon University.

TYKHONOV, D, Jonker, C, Meijer, S and Verwaart, T (2008), Agent-Based Simulation of the Trust and Tracing Game for Supply Chains and Networks. Journal of Artificial Societies and Social Simulation 11(3) 1 https://www.jasss.org/11/3/1.html.

UZZI, B (1997), Social Structure and Competition in Interfirm Networks: The Paradox of Embeddedness. Administrative Science Quarterly, 42(1), pp. 35-67.

VLACHOS, P I and Bourlakis, M (2006), Supply chain collaboration between retailers and manufacturers: Do they trust each other?. Supply Chain Forum: An International Journal, 7(1), pp. 70-80.

----

ButtonReturn to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2009]