Patrick Groeber, Frank Schweitzer and Kerstin Press (2009)
How Groups Can Foster Consensus: The Case of Local Cultures
Journal of Artificial Societies and Social Simulation
vol. 12, no. 2 4
<https://www.jasss.org/12/2/4.html>
For information about citing this article, click here
Received: 17-Aug-2008 Accepted: 23-Jan-2009 Published: 31-Mar-2009
 Abstract
Abstract| |xi (t)-xj (t)|< ε | (1) |
|
xi (t+1)=xi (t)+μ(xi (t)-xj (t)) xj (t+1)=xj (t)+μ(xj (t)-xi (t)) |
(2) |
The speed of approach in behaviour depends on the parameter μ. It reflects the well-established phenomenon that interacting parties become more similar (e.g. Axelrod 1997; Macy and Skvoretz 1998; McPherson et al. 2001; Strang and Soule 1998).
| xi eff (t)=(1-ai (t)) xi (t) + ai (t) xi I | (3) |
at time t. The use of the mean behaviour is chosen to mirror that the agent is equally interested in interacting with any of her past partners.[10]
| ai (t)=|Ii (t)| (|Ii (t)|+1)-1 | (4) |
Hence, we assume that each agent puts equal weight on her own and each in-group member's behaviour. If i has never interacted with another agent, her in-group is empty (|Ii (t)|=0) implying ai=0. Hence, the effective behaviour of agent i is identical to her behaviour (xi eff =xi). Further, ai approaches 1 with growing in-group size |Ii|. If the in-group is large, i 's effective behaviour will therefore tend towards the average in-group behaviour.
| |xi eff (t)-xj eff (t)| < ε | (5) |
If two agents with empty in-groups interact, this is identical to Eq. (1) as xi eff =xi and xj eff =xj for Ii=Ij=[].
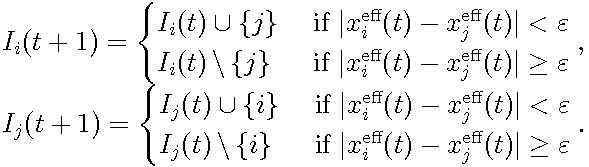
|
(6) |
Note that the in-group relation is symmetric but may not be transitive, i.e. agent i being contained in agent j 's in-group and agent j being contained in agent k 's in-groups does not require k being in j 's in-group.
|
|
| Figure 1a | Figure 1b |

|
|
| Figure 1c | Figure 1d |
|
|
| Figure 1e | Figure 1f |
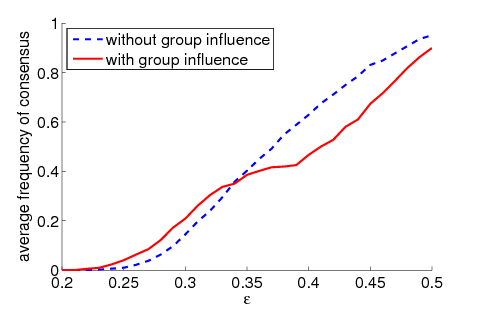
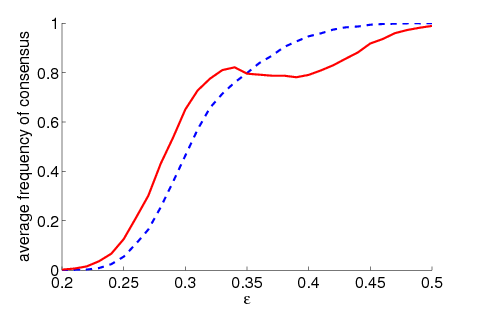
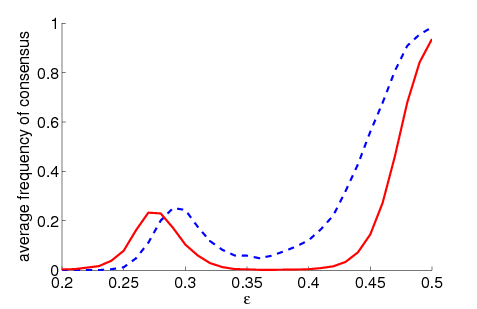
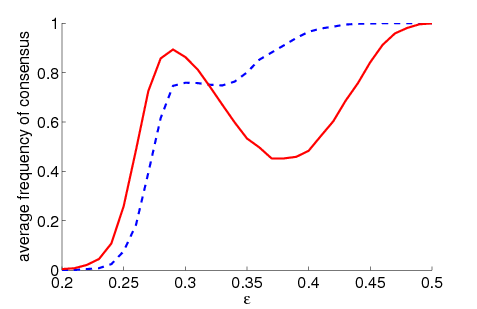
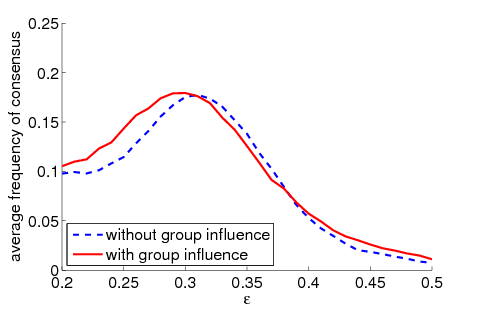
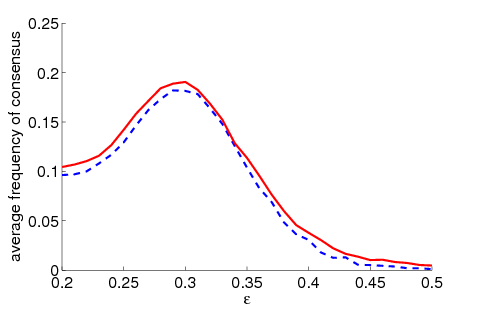
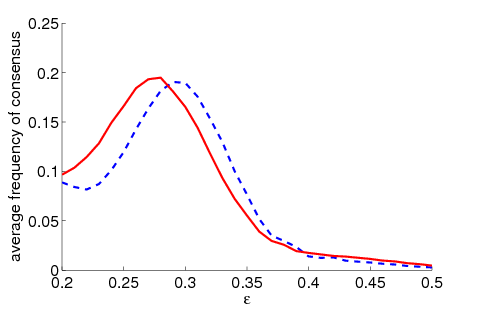
| Figure 1. Average frequency of consensus dependent on ε for 5000 runs and different values of n and μ. The agents' initial behaviour is random according to a uniform distribution; the initial network is empty. For narrow-minded agents (small ε), the group influence fosters consensus while for open-minded agents (high ε), the probability of identical behaviour is lower than in the baseline model | |
|
|
| Figure 2a | Figure 2b |
|
|
| Figure 2c | Figure 2d |
|
|
| Figure 2e | Figure 2f |
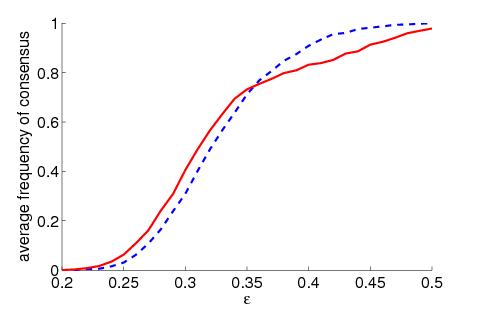
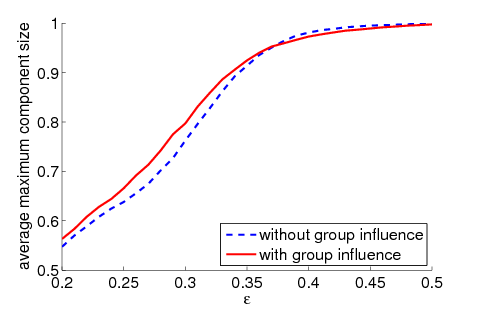
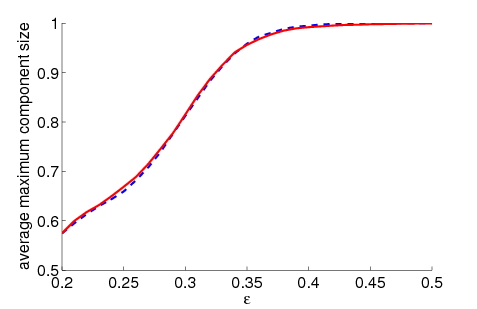
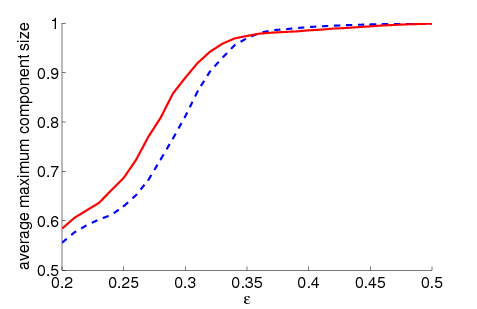
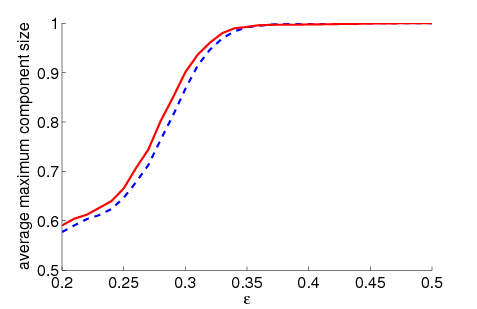
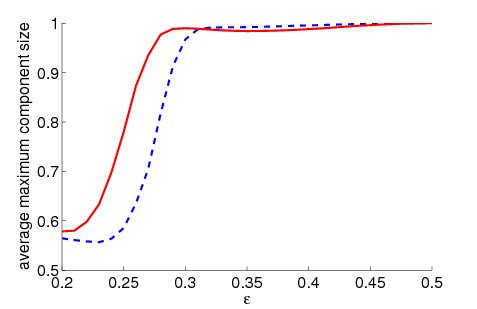
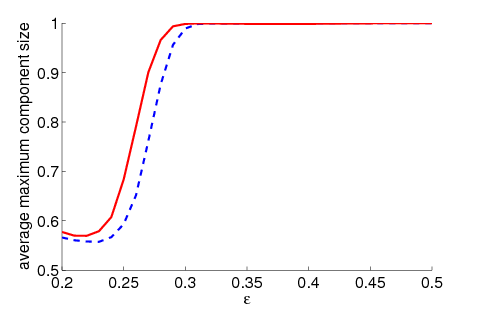
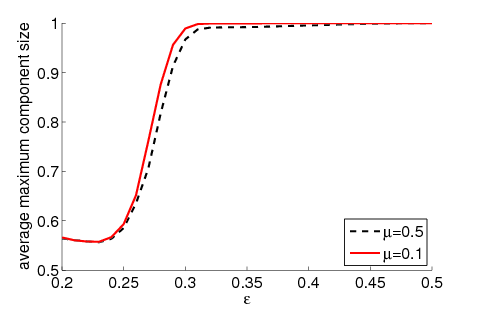
| Figure 2. Average maximum relative component size dependent on ε for 5000 runs and different values of n and μ. The agents' initial behaviour is random according to a uniform distribution; the initial network is empty. For narrow-minded agents (small ε), our model increases the average maximum component size compared to the baseline model without group influence. For open-minded agents (high ε), there is almost no difference between the models with respect to the average maximum component size | |
|
|
| Figure 3a | Figure 3b |
|
|
| Figure 3c | Figure 3d |
|
|
| Figure 3e | Figure 3f |
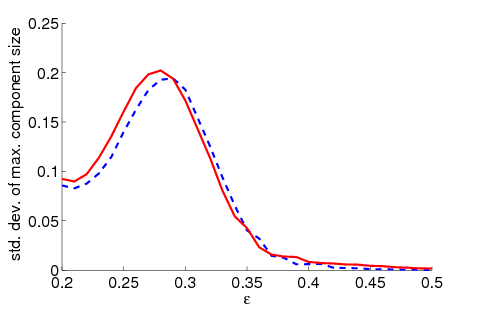
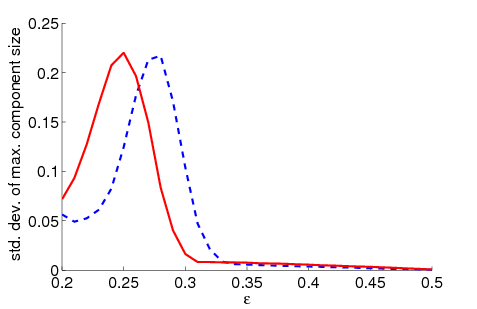
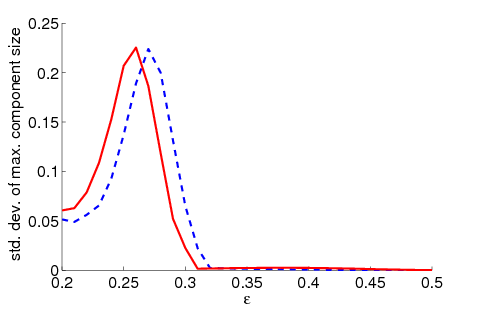
| Figure 3. Standard deviation of the maximum relative group size dependent on ε for 5000 runs and different values of n and μ. The agents' initial behaviour is random according to a uniform distribution; the initial network is empty | |
|
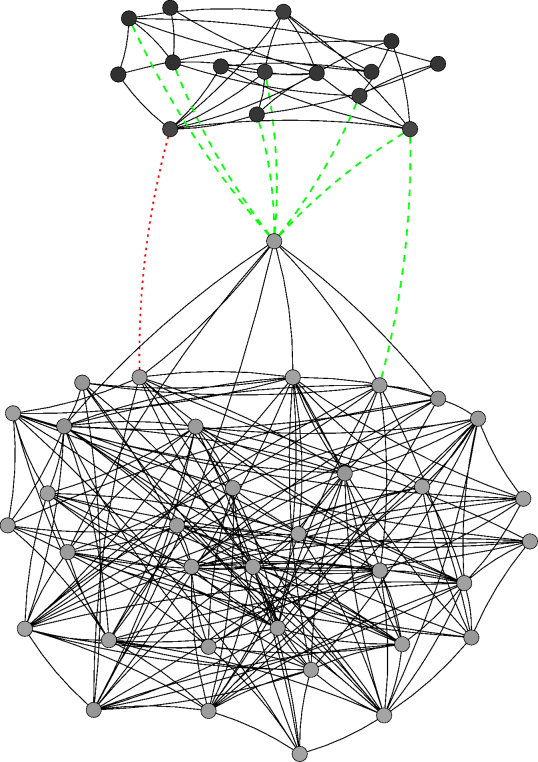
|
| Figure 4a | Figure 4b |
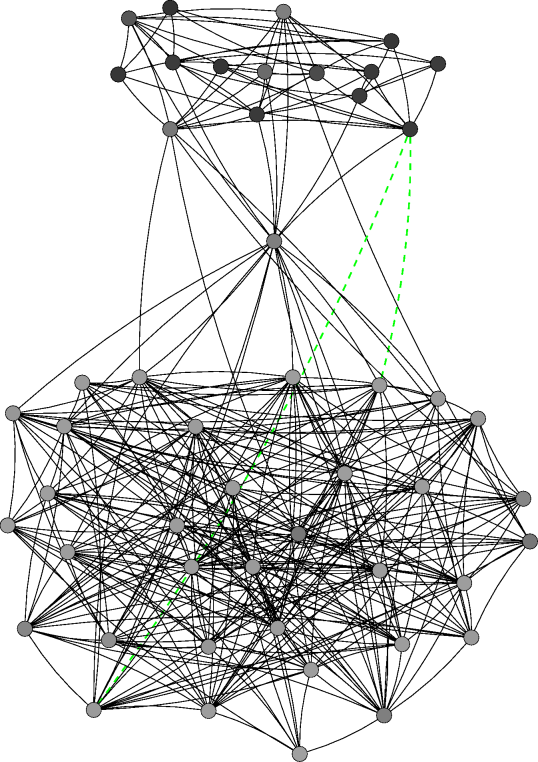
|
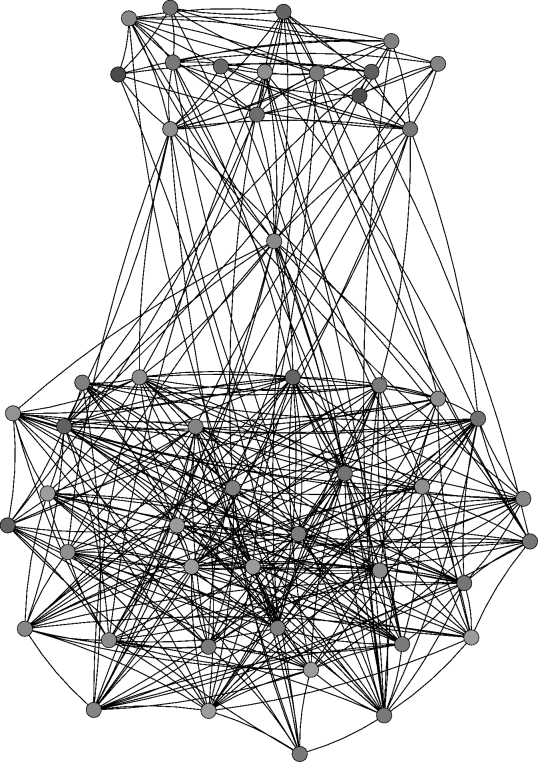
|
| Figure 4c | Figure 4d |
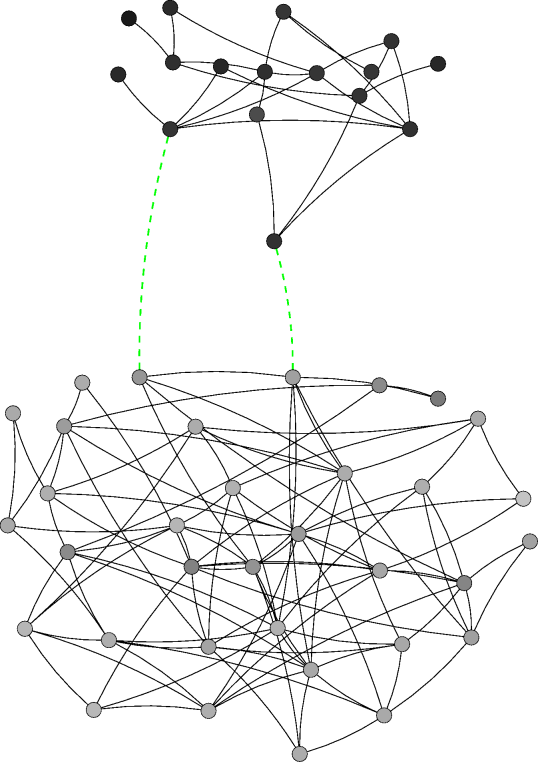
| Figure 4. Network evolution for a simulation with 50 agents and ε=0.3 at different time steps. Note: The agents' initial behaviour is determined randomly according to a uniform distribution the initial network is empty. A node's colour indicates the respective agent's behaviour (white=0, black=1). A green dashed link denotes that the respective agents' difference in effective behaviour is below the threshold while their respective own behaviours differ more than ε. Thus, such a link persists in the local cultures model but would be deleted in the baseline model. A red dotted link indicates that the respective agents' difference in effective behaviour is above the threshold, i.e. the link would be deleted if the respective agents were chosen at that time step | |
|
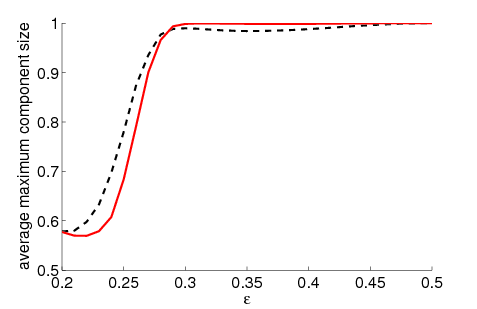
|
| Figure 5a | Figure 5b |
| Figure 5. Average maximum relative component size dependent on ε for 5000 runs, 500 agents and different values of μ. The agents' initial behaviour is random according to a uniform distribution; the initial network is empty. For the baseline model without group influence (5a), a decrease of the convergence speed μ leads to an increase of the maximum component size for all ε. This holds only for open-minded agents (high ε) in case of our model (5b). | |
2 Competitors experiment with different strategies under identical conditions. This allows for direct comparisons of performance and selection of best practice. In addition, firms tackling the same or related problems may exchange knowledge through various mechanisms (Allen 1983). Both aspects contribute to knowledge spillovers. Finally, many firms in a cluster increase the quality of the local labour pool by training activity and immigration of skilled people.
3 Investment research and training requires an understanding that allows firms to capitalise on it, i.e. no exploitation of others' efforts or hiring away of personnel trained elsewhere.
4 Candidate mechanisms are repeated games, reputation formation, signalling or punishment (Nowak 2006). To be effective, consensus about the behaviour that ought to be adopted is needed (e.g. cooperation). To some, this would already constitute a norm (Opp 2001). In addition to strong information requirements, game-theoretic approaches thus need a general co-operation 'norm' to identify defectors.
5 Stark et al 2008a, b have discussed a modification to the linear voter model, where agents become more reluctant to change their current opinion the longer they have it. It was shown that this deceleration of individual dynamics may, for certain growth rates of reluctance, even accelerate the formation of consensus at the system level. This counterintuitive result is partly due to agent heterogeneity, i.e. differences in their individual behaviour.
6 Deffuant et al. 2005 extend the mechanism to study innovation diffusion. For a survey of results in bounded confidence models see Lorenz 2007.
7 Fent et al 2007 have investigated the role of in- and out-group interaction (in a fixed network) for the emergence of social norms. Under certain conditions, convergence towards a single norm, coexistence of two opposing norms, and coexistence of a multitude of norms can be found. The key element was a local utility maximization, where agent i seeks to maximise similarities with her in-group, while minimising the disutilities from the out-group in her social network.
8 The greatest losses often result from diverging strategies (e.g. prisoner's dilemma).
9 As in Moscovici and Doise 1992, where opinions too far from the majority don't enter group discussion.
10 This treatment of group influence by averaging has a long tradition. Formal models of group decision-making (French 1956; Harary 1959; Hegselmann and Krause 2002; Lehrer 1975; Lehrer and Wagner 1981; Wagner 1978) account for group influence by weighted averages. Social impact theory (Latané 1981; Latané and Nowak 1997) also constructs group influence by averaging. Similar to social impact theory, our model features a decreasing marginal group influence with in-group size.
11 Many models in sociology build upon a reciprocal link of behaviour and interaction. See Carley 1991; Coleman 1961; Coleman 1980; Ennett and Baumann 1994; Friedkin and Johnsen 1990; Marsden and Friedkin 1993 or Nowak et al. 1990 among others.
12 For both models, this does not hold in general as the probability of consensus and the average maximum component size as a function of ε are not monotonically increasing (see Ben-Naim et al. 2003 for the baseline model).
13 A video of the simulation is available online. It uses the arf algorithm for dynamic network layout (Geipel 2007). For viewing the video, go to http://web.sg.ethz.ch/publications/local_cultures/web-cultures.html
14 This increase would have two reasons: first the increase of their own behaviour, second the decrease of their lower component's neighbours' influence on their effective behaviour as the share of lower component agents of the neighbourhood also decreases.
ASCH, S.E. (1956). Studies of independence and conformity: I, a minority of one against a unanimous majority. Psychological Monographs 70(9), 1-70.
AXELROD, R. (1986). An evolutionary approach to norms. The American Political Science Review 80(4), 1095-1111.
AXELROD, R. (1997). The Dissemination of Culture: A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution 41, 203-226.
BEN-NAIM, E.; Redner, S.; Kaprivsky, P.L. (2003). Bifurcation and Patterns in Compromise Processes. Physica D 183, 190-204.
CARLEY, K. (1991). A Theory of Group Stability. American Sociological Review 56(3), 331-354.
COASE, R.H. (1937). The nature of the firm. Economica 4(16), 386-405.
COLEMAN, J.S. (1961). The adolescent society: the social life of the teenager and its impact on education. New York: Free Press.
COLEMAN, J.S. (1980). Friendship and the peer group in adolescence. In: J. Adelson (ed.), Handbook of adolescent psychology, New York: Wiley. pp. 408-431.
COLEMAN, J.S. (1990). Foundations of Social Theory. Cambridge MA: Harvard University Press.
DEFFUANT, G.; Huet, S.; Amblard, F. (2005). An individual-based model of innovation diffusion mixing social value and individual benefit. American Journal of Sociology 110(4).
DEFFUANT, G.; Neau, D.; Amblard, F.; Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems 3, 87-98.
DEGROOT, M.H. (1974). Reaching a Consensus. Journal of the American Statistical Association 69(345), 118-121.
DEMSETZ, H. (1967). Towards a theory of property rights. American Economic Review 57(2), 347-359.
ELLISON, G.; Glaeser, E. (1997). Geographic Concentration in U.S. Manufacturing Industries: A Dartboard Approach. Journal of Political Economy 105(5), 889-927.
ENNETT, S.T.; Baumann, K.E. (1994). The contribution of influence and selection to adolescent peer group homogeneity: The case of adolescent cigarette smoking. Journal of Personality and Social Psychology 67(4), 653-663.
FEHR, E.; Fischbacher, U. (2004). Third-party punishment and social norms. Evolution and Human Behaviour 25, 63-87.
FENT, T.; Groeber, P.; Schweitzer, F. (2007). Coexistence of Social Norms based on In- and Out-group Interactions. Advances of Complex Systems 10, 271-286 .
FRENCH, J. (1956). A formal theory of social power. Psychological Review 63, 181-194.
FRIEDKIN, N.; Johnsen, J. (1990). Social influence and opinions. Journal of Mathematical Sociology 15, 193-205.
GEIPEL, M. (2007). Self-Organization applied to Dynamic Network Layout. International Journal of Modern Physics C 18(10).
HARARY, F. (1959). A criterion for unanimity in French's theory of social power. In: D. Cartwright (ed.), Studies in Social Power, Ann Arbour: Institute for Social Research.
HEGSELMANN, R.; Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis, and simulation. Journal of Artificial Societies and Social Simulation 5(3).
HEIDUK, G.; Pohl, N. (2002). Silicon Valley's Innovative Milieu: A Cultural Mix of Entrprepreneurs or an Entrepreneurial Mix of Cultures?, Erkunde, 56(3), 241-252.
HOLLÄNDER, H. (1990). A Social Exchange Approach to Voluntary Cooperation. American Economic Review 80(December), 1157-1167.
HORNE, C. (2001). Sociological perspectives on the emergence of norms. In: M. Hechter; K. Opp (eds.), Social Norms, Russell Sage Foundation. pp. 3-34.
KANDEL, E.; Lazear, E.P. (1992). Peer Pressure and Partnership. Journal of Political Economy 100(4), 801-817.
KOFORD, K.J.; Miller, J.B. (1991). Social Norms and Economic Institutions. Ann Arbour, MI: University of Michigan Press.
LATANÉ, B. (1981). The psychology of social impact. American Psychologist 36, 343-356.
LATANÉ, B.; Nowak, A. (1997). Self-organizing social systems: Necessary and sufficient conditions for the emergence of clustering, consolidation and continuing diversity. In: G.A. Barnett; F.J. Boster (eds.), Progress in Communication Sciences: Advances in Persuasion, London: Ablex Publishing Corporation. pp. 43-74.
LEHRER, K. (1975). Social consensus and rational agnoiology. Synthese 31, 141-160.
LEHRER, K.; Wagner, C.G. (1981). Rational Consensus in Science and Society. Dordrecht: D. Reidl Publishing Co.
LORENZ, J. (2006). Consensus Strikes Back in the Hegselmann-Krause Model of Continuous Opinion Dynamics under Bounded Confidence. Journal of Artificial Societies and Social Simulation 9(1).
LORENZ, J. (2007). Continuous Opinion Dynamics Under Bounded Confidence: A Survey. International Journal of Modern Physics C 18(12), 1819-1838.
LORENZ, J. (2008). Heterogeneous bounds of confidence: Meet, Discuss and Find Consensus! http://arxiv.org/abs/0801.1399v1
MACY, M.W.; Skvoretz, J. (1998). The Evolution of trust and cooperation between strangers: A computational model. American Sociological Review 63(5), 638-660.
MARSDEN, P.; Friedkin, N. (1993). Network studies of social influence. Sociological Methods and Research 22, 127-151.
MASKELL, P. (2001). Towards a Knowledge-based Theory of the Geographical Cluster. Industrial and Corporate Change 10(4), 921-943.
MCPHERSON, M.; Smith-Lovin, L.; Cook, J.M. (2001). Birds of a Feather: Homophily in Social Networks. Annual Review of Sociology 27, 415-444.
MOSCOVICI, S.; Doise, W. (1992). Dissension et consensus: Une théorie générale des décisions collectives. Paris: Presses Universitaires de France.
NOWAK, A.; Jacek, S.; Latané, B. (1990). From private attitude to public opinion: A dynamic theory of social impact. Psychological Review 97, 362-376.
NOWAK, M.A. (2006). Five rules for the evolution of cooperation. Science 314(5805), 1560-1563.
OPP, K. (1982). The evolutionary emergence of norms. British Journal of Social Psychology 21, 139-149.
OPP, K. (2001). How Do Social Norms Emerge? An Outline of a Theory. Mind and Society 2, 101-128.
PORTER, M.E. (1990). The Competitive Advantage of Nations. London: Macmillan.
PUJOL, J.; Delgado, J.; Sangüesa, R.; Flache, A. (2005). The Role of Clustering on the Emergence of Efficient Social Conventions. In: Proceedings of the 19th International Joint Conference on Artificial Intelligence IJCAI-05. Edinburgh, Scotland, pp. 965-970.
PYKE, F.; Beccattini, G.; Sengenberger, W. (1990). Industrial districts and inter-firm co-operation in Italy. Geneva: International Institute for Labour Studies.
SAXENIAN, A. (1994). Regional Advantage: Culture and Competition in Silicon Valley and Route 128. Cambridge, Mass.: Harvard University Press.
SCHWEITZER, F. (2007). Collective Decisions in Multi-Agent Systems. In: S. Takahashi; D. Sallach; J. Rouchier (eds.), Advancing Social Simulation: The First World Congress, Tokyo: Springer. pp. 7-12.
SCHWEITZER, F.; Behera, L. (2009). Nonlinear voter models: The transition from invasion to coexistence. European Physical Journal B 67.
SHERIF, M. (1973). The Psychology of Social Norms. New York: Octagon Books.
SHOHAM, Y.; Tennenholtz, M. (1992). Emergent Conventions in Multi-Agent Systems: Initial Experimental Results and Observations. In: Proceedings of Knowledge Representation and Reasoning. pp. 225-231.
SMITH, A. (2003). The Wealth of Nations (1776). Bantam Classic, New York: Bantam Dell.
STARK, H.-U.; Tessone, C.J.; Schweitzer, F. (2008a). Decelerating microdynamics can accelerate macrodynamics in the voter model. Physical Review Letters 101(1), 018701(4).
STARK, H.-U.; Tessone, C.J.; Schweitzer, F. (2008b). Slower is Faster: Fostering Consensus Formation by Heterogeneous Inertia. Advances in Complex Systems 11(4).
STRANG, D.; Soule, S.A. (1998). Diffusion in organizations and social movements: From hybrid corn to poison pills. Annual Review of Sociology 24, 265-290.
SUGDEN, R. (1989). Spontaneous Order. The Journal of Economic Perspectives 3(4), 85-97.
ULLMANN-MARGALIT, E. (1977). The Emergence of Norms. Clarendon Press.
VAN Tulder, R. (1988). Small European countries in the International Telecommunications Struggle. In: C. Freeman; B.-A. Lundvall (eds.), Small Countries Facing the Technological Revolution, London, Pinter Publishers, pp. 169-183.
VOSS, T. (2001). Game theoretical perspectives on the emergence of social norms. In: M. Hechter; K.-D. Opp (eds.), Social Norms, New York: Russell Sage Foundation. pp. 105-136.
WAGNER, C.G. (1978). Consensus through respect: A model of rational group decision-making. Philosophical Studies 34, 335-349.
WEBER, M. (1999). Essays in economic sociology. Princeton NJ: Princeton University Press.
WILLIAMSON, O.E. (1975). Markets and Hierarchies - Analysis and Anti-Trust Implications. New York: Free Press.
ZIEGLER, R. (2007). The Kula Ring of Bronislaw Malinowski. Bayerische Akademie der Wissenschaften.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2009]