Conrad Power (2009)
A Spatial Agent-Based Model of N-Person Prisoner's Dilemma Cooperation in a Socio-Geographic Community
Journal of Artificial Societies and Social Simulation
vol. 12, no. 1 8
<https://www.jasss.org/12/1/8.html>
For information about citing this article, click here
Received: 28-May-2008 Accepted: 01-Dec-2008 Published: 31-Jan-2009
 Abstract
Abstract| Table 1: Payoff Matrix for a General Prisoner's Dilemma Game | |||
| Player A | |||
Player B | Cooperate | Defect | |
| Cooperate | R, R | S, T | |
| Defect | T, S | P, P | |
| Table 2: Payoff Matrix for an Example Iterated Prisoner's Dilemma Game | |||
| Player A | |||
Player B | Cooperate | Defect | |
| Cooperate | 3, 3 | 0, 5 | |
| Defect | 5, 0 | 1, 1 | |
|
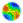
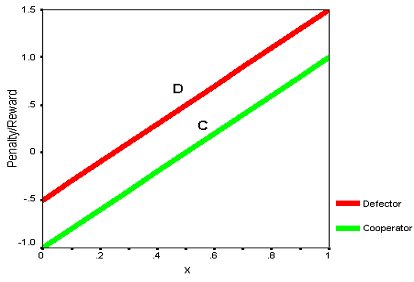
| Figure 1. N-Person Prisoner's Dilemma Payoff Functions for Preferred Defection and Un-Preferred Cooperation, Relative to the Number of Other Players that Decide to Cooperate: (from Akimov and Southchanski 1994) |
|
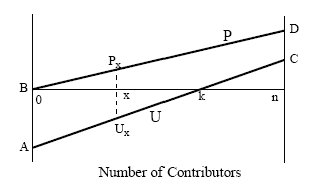
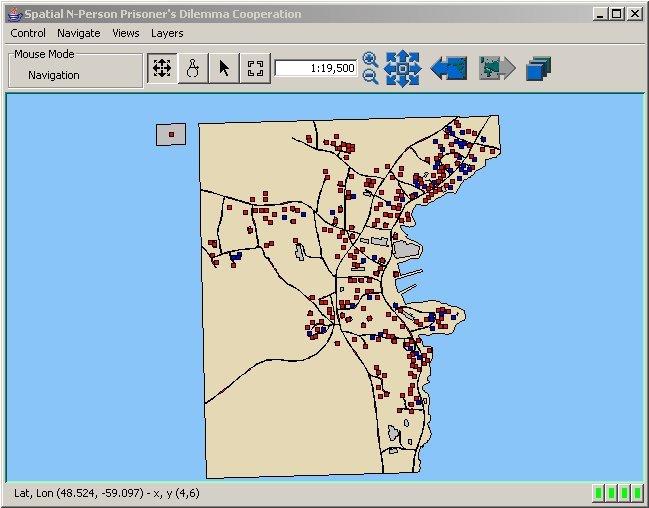
| Figure 2. Interface of the Spatial Agent-Based Model of NPPD Cooperation |
|
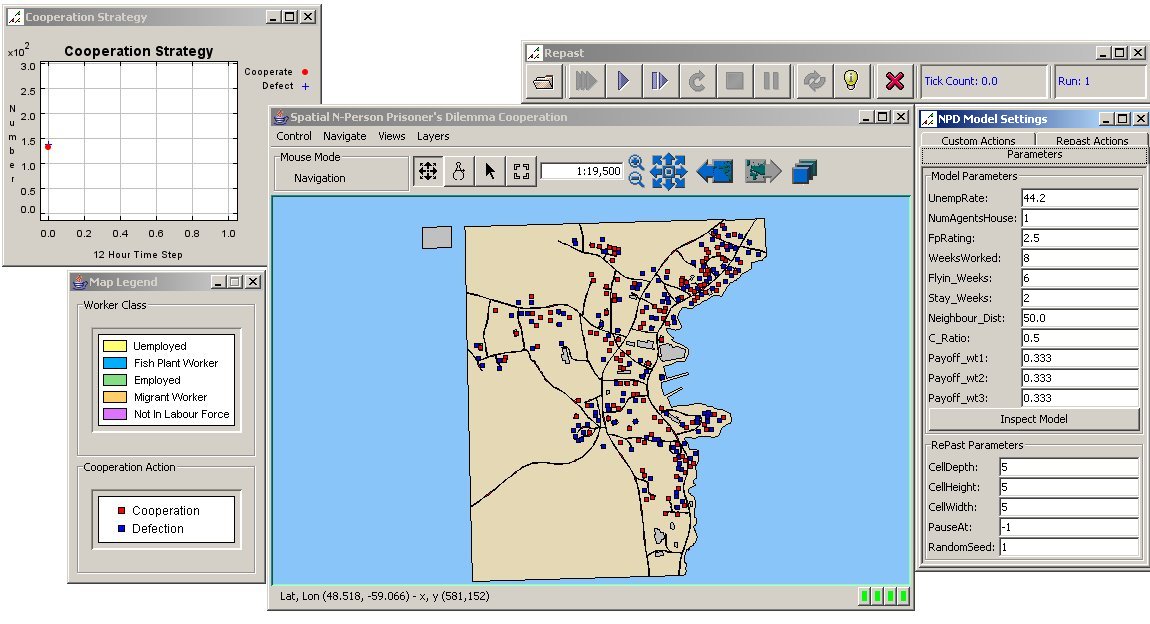
| Figure 3. Analyzed Environment of Central Catalina, Newfoundland and Labrador, Canada |
|
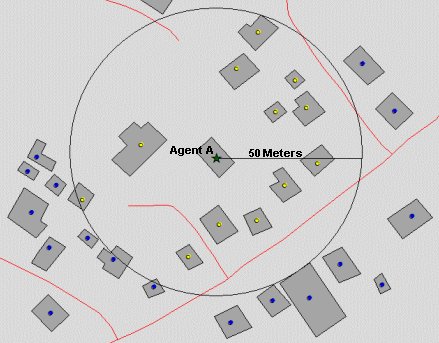
| Figure 4. Configuration of a 50 Meter Neighbourhood Buffer of Agent A |
| D = -0.5 + 2x | (1) |
| C = -1 + 2x | (2) |
where x represents the ratio of the number of cooperators to the total number of neighbours. The stochastic factor is a parameter that accounts for any uncertainty in the agent interactions and noise in the environment. When dealing with linear payoff functions, stochasticity is applied by thickening the width of each line relative to the y axis to produce a range of payoffs for a cooperation ratio. For example, an agent with previous action C in a neighbourhood with 0.60 cooperation receives a payoff reward of 0.207 ± 0.033. A line drawn from the bottom of the C function intersects the payoff axis at 0.174 while a line from the top of C hits the axis at 0.24. The derived cooperation value will be a random value chosen within the range of 0.174 to 0.24. In a deterministic environment where the stochastic factor is zero, the width of the payoff function would be and the payoff reward would equal 0.207.
|
| Figure 5. Reward/Penalty Payoff Functions for Pavlovian Defectors and Cooperators (from Szilagyi 2003) |
|
|
(3) |
,where Wi is a weighting parameter such that all weights sum to one, and Mci is the history payoff (i.e. Mc1 stores the current payoff). Assuming that the effects of memory decrease with time, W1 ≥ W2 ≥W3.
| p( t+1) = p( t) + (1-p( t)) * α i, if at time t, S(t) = C and RPwt > 0 | (4) |
| p( t+1) = (1-α i) * p( t), if at time t, S(t) = C and RPwt ≤ 0 | (5) |
Note that for every t there must be q( t) = 1 - p( t). The same set of equations are also used for updating the action probabilities when the previous action is D:
| q( t+1) = q( t) + (1-q( t)) * α i, if at time t, S(t) = D and RPwt > 0 | (6) |
| q( t+1) = (1-α i) * q(t), if at time t, S(t) = D, and RP wt ≤ 0 | (7) |
|
|
(8) |
where Cj is the payoff value for agent j and N is the total number of agents in the neighbourhood. The average neighbourhood function for three memory events is formulated as:
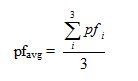
|
(9) |
Thus, the state of agent i at time t+1 with S( t):
|
For S(t) = C:
S( t+1) =
|
(10) |
|
For S(t) = D:
S( t+1) =
|
(11) |
,where Ru∈ [0,1] is a uniform random value.
|
| Figure 6. Map of Cooperation Pattern for Mobile Agents in a 50 Meter Neighbourhood |
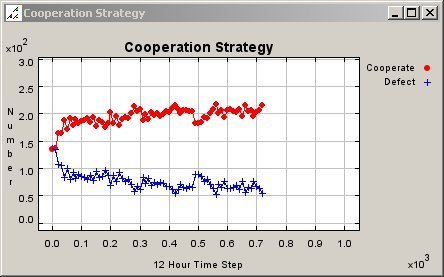
|
| Figure 7. Graph of Cooperation Pattern for Mobile Agents in a 50 Meter Neighbourhood |
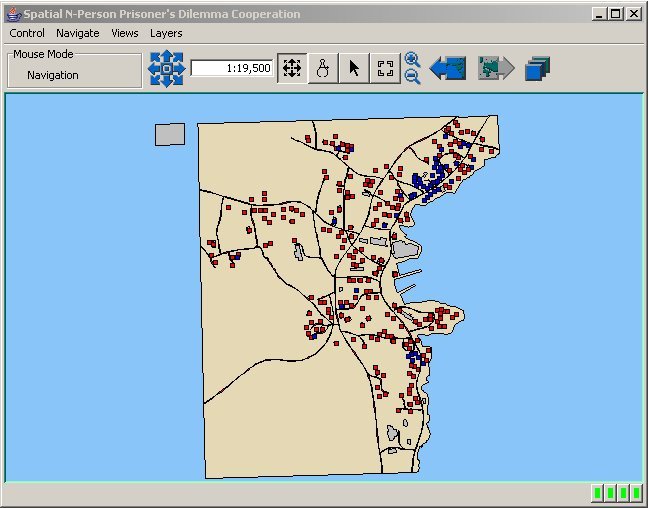
|
| Figure 8. Map of Cooperation Pattern for Fixed Agents in a 50 Meter Neighbourhood |
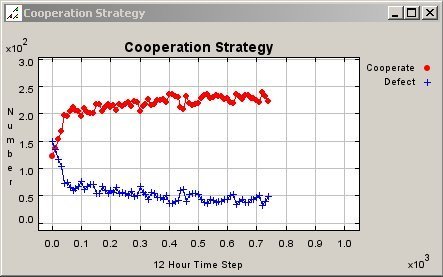
|
| Figure 9. Graph of Cooperation Pattern for Fixed Agents in a 50 Meter Neighbourhood |
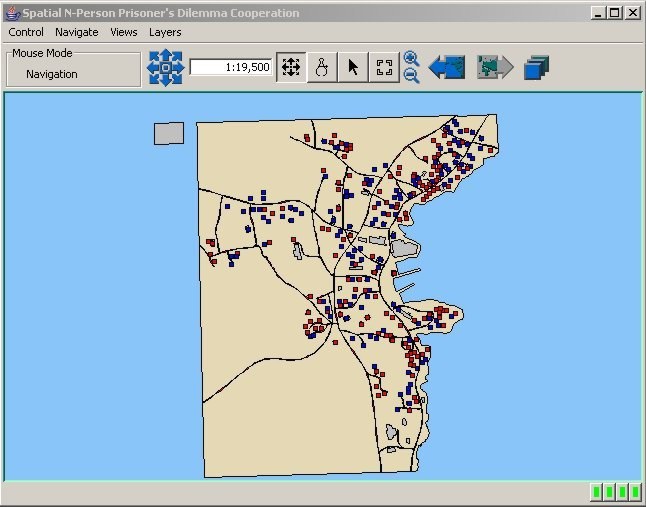
|
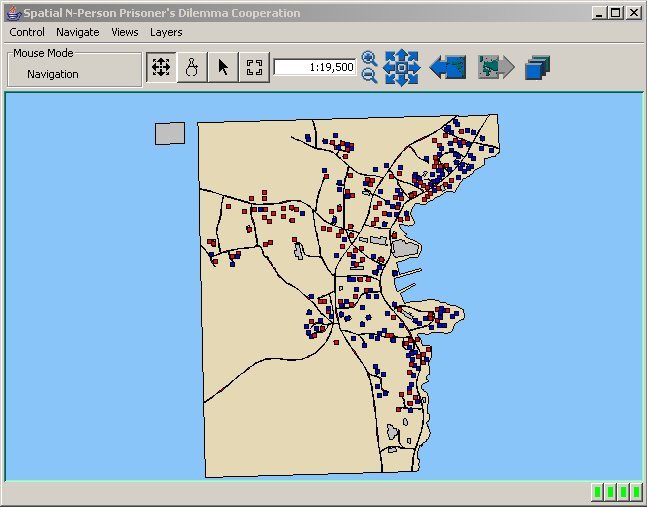
| Figure 10. Map of Cooperation Pattern for Mobile Agents in a 150 Meter Neighbourhood |
|
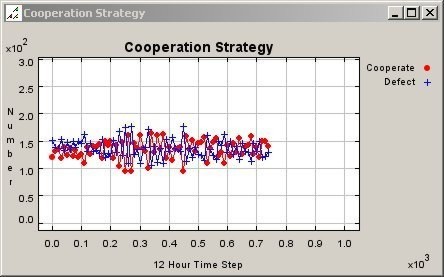
| Figure 11. Graph of Cooperation Pattern for Mobile Agents in a 150 Meter Neighbourhood |
|
| Figure 12. Map of Cooperation Pattern for Fixed Agents in a 150 Meter Neighbourhood |
|
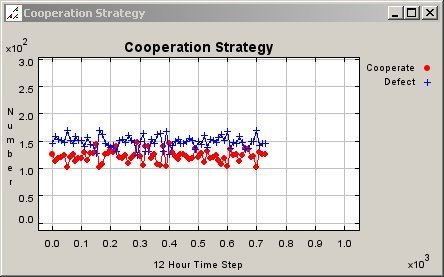
| Figure 13. Graph of Cooperation Pattern for Fixed Agents in a 150 Meter Neighbourhood |
|
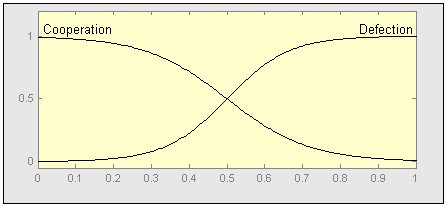
| Figure 14. Fuzzy Membership Functions of Cooperation and Defection |
ALONSO, J., A. Fernandez, and H. Fort (2006). Prisoner's Dilemma Cellular Automata Revisited: Evolution of Cooperation Under Environmental Pressure. Journal of Statistical Mechanics: Theory and Experiment, 13, pp. 1-15.
AXELROD, Robert (1984). The Evolution of Cooperation. New York: Basic Books Publishing.
AXELROD, Robert (1997). The Complexity of Cooperation: Agent-Based Models of Competition and Cooperation. Princeton, New Jersey: Princeton University Press.
BENENSON, Itzhak, and Paul Torrens (2004). Geosimulation: Automata-Based Modeling of Urban Phenomena. West Sussex, England: John Wiley and Sons Ltd.
BOONE, C., B. De Brabander, and A. van Witteloosluijn (1999). The Impact of Personality on Behavior in Five Prisoner's Dilemma Games. Journal of Economic Psychology, 28, pp. 343-377.
BOYD, R., and J. Lorderbaum (1987). No Pure Strategy is Evolutionary Stable in the Repeated Prisoner's Dilemma Game. Nature, 32(6117), pp. 58-59.
BREMBS, Bjorn (1996). Chaos, Cheating, and Cooperation: Potential Solutions to the Prisoner's Dilemma. OIKOS 76, 1, pp. 14-24.
BROWN, D. G., R. Riolo, D.T. Robinson, M. North, and W. Rand (2005). Spatial Process and Data Models: Toward Integration of Agent-Based Models and GIS. Journal of Geographical Systems, Special Issue on Space-Time Information Systems, 7(1), pp. 25-47.
COHEN, Michael D., Rick L. Riolo, and Robert Axelrod (1998). The Emergence of Social Organization in the Prisoner's Dilemma: How Context Preservation and Other Factors Promote Cooperation. Santa Fe Institute Working Paper 99-01-002.
COUCLELIS, Helen (2001). Why I No Longer Work with Agents: A Challenge for ABMs of Human-Environment Interactions. In Parker, D.C., Berger, T. and Manson, S.M. (Eds.) Meeting the Challenge of Complexity: Proceedings of a Special Workshop on Land-Use/Land-Cover Change, Irvine, California.
ECKERT, Daniel, Stefan Koch, and Johann Mit_hner (2005). Using the Iterated Prisoner's Dilemma for Explaining the Evolution of Cooperation in Open Source Communities. Proceedings of the First International Conference on Open Source Systems, Genova, July 11-15.
FORT, Hugo, and Nicolás Pérez (2005) The Fate of Spatial Dilemmas with Different Fuzzy Measures of Success, Journal of Artificial Societies and Social Simulation, 8(3)1, https://www.jasss.org/8/3/1.html
GEOTools 2.4.4 (2008). Open Source Java GIS Toolkit. http://geotools.codehaus.org/.
HARDEN, Garett (1968). The Tragedy of the Commons. Science, 162, pp. 1243-1248.
HAUERT, C. and H.G. Schuster (1997) Effects of Increasing the Number of Players and Memory Size in The Iterated Prisoner's Dilemma: A Numerical Approach. Proceedings of the Royal Society of London B, 264, pp. 513-519.
JAVA Topology Suite 1.8 (2007). Vivid Solutions. http://www.vividsolutions.com/jts/jtshome.htm.
KEHAGIAS, A (1994). Probabilistic Learning Automata and the Prisoner's Dilemma. http://users.auth.gr/~kehagiat/KehPub/other/1994JLA1.pdf.
KILLINGBACK, Timothy, and Michael Doebeli (2002). The Continuous Prisoner's Dilemma and the Evolution of Cooperation through Reciprocal Altruism with Variable Investment. The American Naturalist, 160(4), pp. 421-438.
LOOMIS, Charles P. (1996). Social Systems: Essays on Their Perspective and Change. Toronto, Canada: D. Van Nostrand Company Inc.
MCCAIN, Roger (2003). Specifying Agents: Probabilistic Equilibrium with Reciprocity. Computing in Economics and Finance, 9, pp. 1-34.
MILINSKI, Manfred, and Claus Wedekind (1998) Working Memory Constrains Human Cooperation in the Prisoner's Dilemma. Proceedings of the National Academy of Science USA, 95, pp. 13755-13758.
NOWAK, Martin A., and Robert M. May (1992). Evolutionary Games and Spatial Chaos. Nature, 359, pp. 826-829.
NOWAK, Martin A., and Karl Sigmund (1992). Tit for Tat in Heterogeneous Population. Nature, 355, pp. 250-253.
NOWAK, Martin A., and Karl Sigmund (1993). A Strategy of Win-Stay, Lose-Shift that Outperforms Tit-For-Tat in the Prisoner's Dilemma Game. Nature, 364, pp. 56-58.
OPENMAP 4.6.3 (2007). BBN Technologies. http://openmap.bbn.com
POWER, Conrad, Alvin Simms, and Roger White (2001). Hierarchical Fuzzy pattern Matching for the Regional Comparison of Landuse Maps. International Journal of Geographical Information Systems, 15(1), pp. 77-100.
RECURSIVE Porous Agent Simulation Toolbox (2007). Java Version 3.0, University of Chicago and Argonne National Laboratory. http://repast.sourceforge.net.
SCHELLING, T.C. (1973). Hockey Helmets, Concealed Weapons, and Daylights Savings. Journal of Conflict Resolution, 13(3), pp. 381-428.
SHAO-MENG Qin, Yong Chen, Xiao-Ying Zhao, and Jian Shi (2008) Memory Effect on Prisoner's Dilemma Game in a Square Lattice. http://arxiv.org/PS_cache/arxiv/pdf/0801/0801.2827v2.pdf
STATISTICS Canada (2006). General Census Release. http://www12.statcan.ca/english/census/index.cfm.
SZILAGYI, Miklos, and Zoltan Szilagyi (2002). Non-Trivial Solutions to the N-Person Prisoner's Dilemma. Systems Research and Behavioral Science, 19(3), pp. 281-290.
SZILAGYI, Miklos (2003). Simulation of Multi-Agent Prisoner's Dilemma. Systems Analysis and Modeling Simulation, 43(6), pp. 829-846.
THORNDIKE, E.L. (1911). Animal Intelligence. Darien, Connecticut: Hafner Press.
TRIVERS, R.L. (1971). The Evolution of Reciprocal Altruism. Quantitative Reviews in Biology, 46, pp. 35-57.
YAO, Xin, and P.J. Darwen (1994). An Experimental Study of N-Person Iterated Prisoner's Dilemma. Informatica, 18, pp. 435-450.
ZEIGLER, B.P., H. Praehofer, and T.G. Kim (2000). Theory of Modeling and Simulation: Integrating Discrete Events and Continuous Complex Dynamic Systems. New York: Academic Press, 2nd Edition.
ZHAO, Jijun, Miklos Szilagyi, and Ferenc Szidarovszky (2007). A Continuous Model of N-Person Prisoner's Dilemma. Game Theory and Applications, 12, pp.207-242.
ZHAO-HAN Sheng, Yun-Zhang Hou, Xiao-Ling Wang, and Jian-Guo Du (2008) The Evolution of Cooperation with Memory, Learning, and Dynamic Preferential Selection in Spatial Prisoner's Dilemma Game. 2007 International Symposium on Nonlinear Dynamics, Journal of Physics: Conference Series 96, pp. 1-6
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2009]