Tatiana Filatova, Dawn Parker and Anne van der Veen (2009)
Agent-Based Urban Land Markets: Agent's Pricing Behavior, Land Prices and Urban Land Use Change
Journal of Artificial Societies and Social Simulation
vol. 12, no. 1 3
<https://www.jasss.org/12/1/3.html>
For information about citing this article, click here
Received: 25-Mar-2008 Accepted: 30-Nov-2008 Published: 31-Jan-2009
 Abstract
Abstract
|
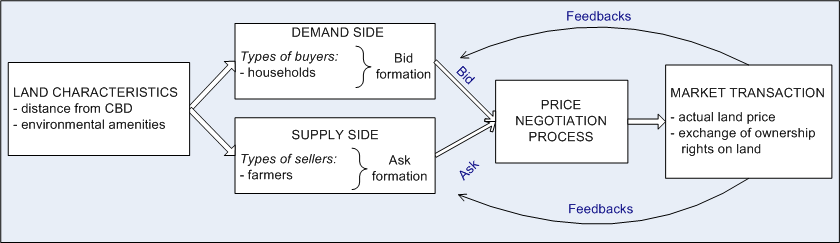
| Figure 1. Conceptual scheme of the land market |
|
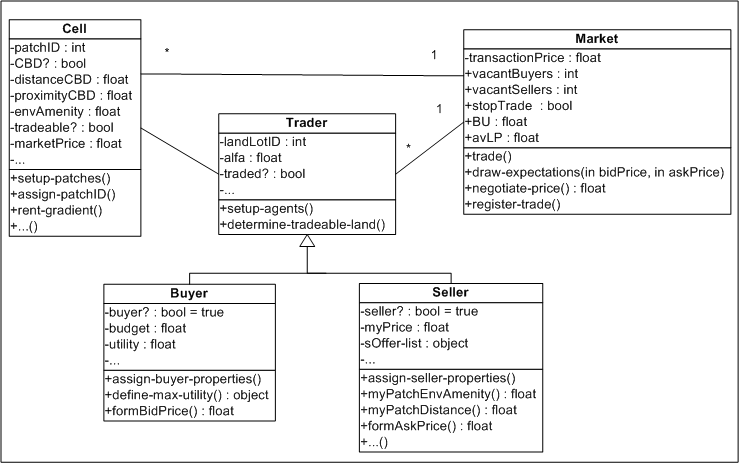
| Figure 2. UML class diagram of the ALMA-v1.0 metamodel[2] |
|
|
(1) |
Further, when agents estimate their utility for a certain property unit, they use a normalized value of proximity:
|
|
(2) |
The standard monocentric model assumes that households choose a location in the city as a result of the tradeoff between land price and transport costs. Transport costs are assumed to be a linear function of distance: T(D)=tcu*D, where tcu are transport costs per unit of distance.
|
|
(3) |
Second, at this point of the model development it is assumed that each seller owns only one spatial good (i.e., one cell) and each buyer is interested only in buying one property unit. We leave for future work the question of the amount of floor space/land lot area demanded.
|
|
(4) |
|
|
(5) |
Here, Y and U are calculated according to Equations (3) and (4) respectively, and b is a constant. Function (5) is monotonically increasing approaching Y as U → ∞, meaning that individual WTP increases with utility but does not exceed her budget. The value of parameter b controls the steepness of the function. As b → ∞ the function (5) becomes flatter, and at U = b, WTP = Y/2, reaching half of its possible value. We can think of b as a proxy of the affordability of all other goods to reflect their relative influence on the WTP for housing. As shown in Appendix A, the WTP function (5) exhibits the main qualitative properties of the neoclassical demand function.
|
|
(6) |
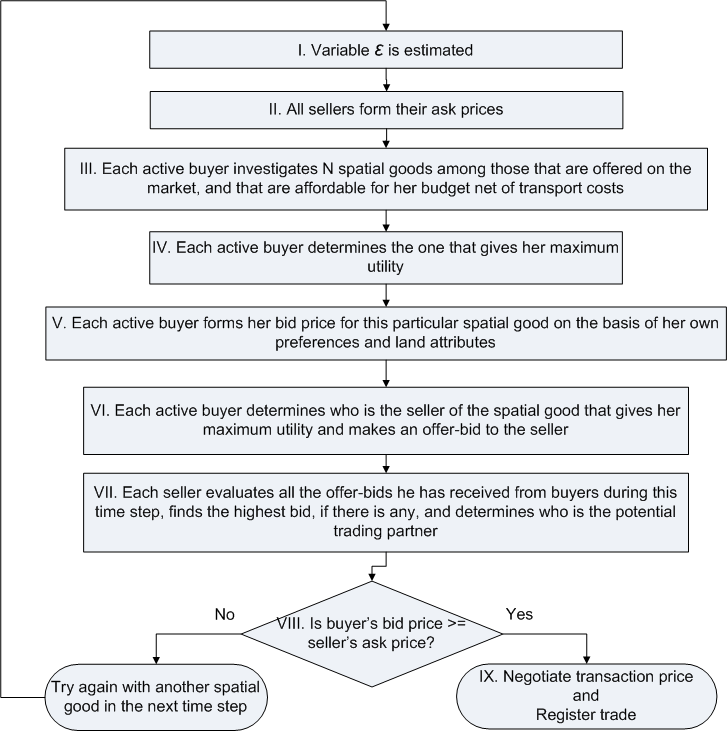
where NB is the number of buyers and NS is the number of sellers. Both variables indirectly depend on land prices and the number of successful transactions in the previous time step, since if prices are beneficial for both buyers and sellers, they participate in successful trades and leave the land market. If an imbalance of buyers and sellers remains, bid or ask prices will adjust to correct the imbalance. At the beginning of each time step, the variable ε is updated and pricing behavior changes (See Figure 3).
|
|
(7) |
The variable ε is estimated as in Equation 6. In the case of a buyer's market, when sellers decrease their ask price ( Pask), we impose a condition that the ask price cannot go below agricultural reservation price ( Pag).
|
| Figure 3. Conceptual algorithm of trade |
|
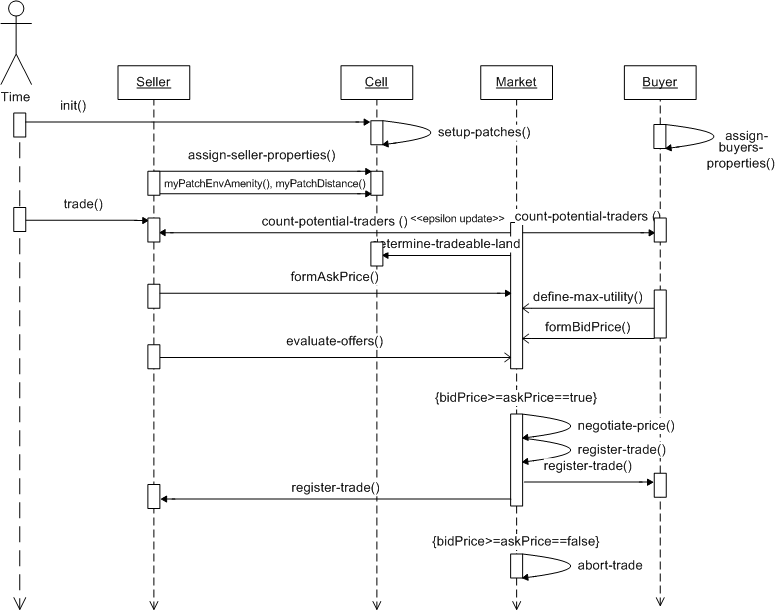
| Figure 4. UML time sequence diagram |
| Table 1: Values of parameters unchanged in the simulation experiments | ||||||
| Symbol | Y | A | b | N of cells | P<sub> | WTA |
| Meaning | Individual budget | Level of green amenities | A constant in (5) | Number of spatial goods in a city | Reservation price for agricultural land | WTA for agricultural land without consideration of the market situation |
| Value | 800 | 1 | 70 | 841 | 200 | 250 |
| Table 2: Description of the performed experiments | |
| Experiment # | Tested hypothesis |
| Exp1 | An agent-based ALMA model with distributed price determination mechanisms reproduces the conventional analytical model behavior given similar assumptions, i.e. structural validation holds. |
| Exp2 | Increased tolerance for commuting among buyers (changes in preferences for distance - _) causes urban expansion. |
| Exp3 | In the case of a "sellers' market" gains from trade will not be divided equally and the city will expand, assuming that buyers adapt their bid prices based on the market situation. |
| Exp4 | The more often buyers are faced with information about market conditions, the more likely they are to "panic" and to offer higher bids. |
| Exp5 | In the case of a "buyers' market" gains from trade will mostly be captured by buyers, assuming that sellers adapt their ask prices based on the market situation. |
| Exp6 | The more often sellers are faced with information about market conditions, the more likely they are to "panic" and to offer lower ask prices. |
| Table 3: Values of parameters changed in the simulation experiments | |||||||
| Symbol | Meaning | Exp1 | Exp2 | Exp3 | Exp4 | Exp5 | Exp6 |
| NB | number of buyers | 841 | 841 | 925 | 925 | 757 | 757 |
| NS | number of sellers | 841 | 841 | 841 | 841 | 841 | 841 |
| MB | market behavior | Pure WTP/WTA | Pure WTP/WTA | Buyers:Market oriented | Buyers:Market oriented | Sellers:Market oriented | Sellers:Market oriented |
| Betta | preference for proximity to the CBD | 0.85 | 0.7 | 0.85 | 0.85 | 0.85 | 0.85 |
| N-buyers in trade | number of buyers activated each trade period, i.e. the speed of epsilon (ε) updating | all | all | all | 5 | all | 5 |
| TCU | transport costs per unit of distance | 1 | 1 | 1 | 1 | 1 | 1 |
| Table 4: Economic and spatial metric outcomes of the ALMA experiments | ||||||
| Parameter | Exp1 | Exp2 | Exp3 | Exp4 | Exp5 | Exp6 |
| Individual utility: Mean | 65.48 | 66.61 | 63.51 | 62.19 | ||
| St.dev | 12.56 | 12.6 | 13.29 | 13.8 | ||
| Aggregate utility | 30448.82 | 38431.14 | 32836.11 | 34391.27 | ||
| Buyers' bid price: Mean | 363.72 | 369.97 | 371.99 | 374.82 | 342.24 | 342.26 |
| St.dev | 73.92 | 73.53 | 80.21 | 80.53 | 83.99 | 83.98 |
| Urban land price: Mean | 306.86 | 309.98 | 311 | 312.41 | 286.35 | 285 |
| St.dev | 36.96 | 36.77 | 40.11 | 40.27 | 44.99 | 45.17 |
| Average surplus %:Buyers' | 50% | 50% | 39.58% | 38.19% | 60.59% | 62.06% |
| Sellers' | 50% | 50% | 60.42% | 61.81% | 39.41% | 37.94% |
| Total property value | 142690.2 | 178860.2 | 160785.6 | 161494.5 | 158350.8 | 157587.1 |
| City size (urban population) | 465 | 577 | 517 | 553 | ||
| Distance at which city border stops | 12.08 | 13.45 | 12.81 | 13.15 | ||
| Table 5: Linear regression estimation results of the ALMA model generated data (the transaction price is a dependent variable) | ||||||
| Parameter | Exp1 | Exp2 | Exp3 | Exp4 | Exp5 | Exp6 |
| R2: | 0.9905 | 0.9858 | 0.9913 | 0.9899 | 0.982 | 0.982 |
| Intercept: estimate | 410.76 | 413.2 | 423.9 | 425.68 | 412.39 | 411.57 |
| St error | 0.09 | 0.1 | 0.09 | 0.1 | 0.14 | 0.14 |
| t-Value | 4498.96 | 4136.46 | 4710.81 | 4360.21 | 2936.39 | 2917.12 |
| Distance to CBD: estimate | -12.81 | -11.43 | -13.2 | -13.25 | -14.25 | -14.31 |
| (slope) St error | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 |
| t-Value | -1207.17 | -1096.03 | -1330.84 | -1230.62 | -951.96 | -951.55 |
|
|
| Figure 5.a. Exp1, Replication of the Alonso model: a) Spatial form of a city |
|
|
| Figure 5.b. Exp1, Replication of the Alonso model: b) Land rent gradient |
|
|
| Figure 5.c. Exp1, Replication of the Alonso model |
|
|
| Figure 6.a. Exp2, Preferences for proximity are lower than in Exp1 in Figure 5: a) Spatial form of a city |
|
|
| Figure 6.b. Exp2, Preferences for proximity are lower than in Exp1 in Figure 5: b) Land rent gradient |
|
|
| Figure 6.c. Exp2, Preferences for proximity are lower than in Exp1: Lad rents |
|
|
| Figure 7[7]. Land rent gradients for Exp1 and Exp2, linear regression fit of the computer generated data TransPr1(2)- actual land transaction prices from Exp1(Exp2 - lower preferences for proximity), Fitted value - estimated land rent gradient |
|
|
| Figure 8.a. Exp3, Buyers' competition in a sellers' market: a) Spatial form of a city |
|
|
| Figure 8.b. Exp3, Buyers' competition in a sellers' market: b) Land rent gradient |
|
|
| Figure 9.a. Influence of the speed of ε updating on the land prices at a sellers' market: a) Land prices, Exp3 |
|
|
| Figure 9.b. Influence of the speed of ε updating on the land prices at a sellers' market: b) Land prices, Exp4 |
|
|
| Figure 10[8]. Land rent gradients for Exp1, Exp3 and Exp4, linear regression fit of the computer generated data TransPr4- actual land transaction prices from Exp4, Fitted value - estimated land rent gradient: blue - for Exp1, black - for Exp3, red - for Exp4 |
|
|
| Figure 11.a. Exp5, Sellers' competition in buyers' market: a) Spatial form of a city |
|
|
| Figure 11.b. Exp5, Sellers' competition in buyers' market: b) Land rent gradient |
|
|
| Figure 12[9]. Land rent gradients for Exp1 and Exp5, linear regression fit of the computer generated data TransPr5- actual land transaction prices from Exp5, Fitted value - estimated land rent gradient: blue - for Exp1, orange - for Exp5, dark green - for Exp6 |
|
|
| Figure 13.a. Influence of the speed of ε updating on the land prices at a buyers' market: a) Land prices, Exp5 |
|
|
| Figure 13.b. Influence of the speed of ε updating on the land prices at a buyers' market: b) Land prices, Exp6 |
|
|
(8) |
This result is in line with microeconomic demand theory, in which an increase in income results in a positive change in the WTP, i.e. the demand curve shifts up. This fact means that if a buyer's purchasing power increases, her WTP also increases.
|
|
(9) |
WTP increases as the utility of the good increases. An individual is willing to pay less for a spatial good that brings her lower utility and more for the one that brings her higher utility.
|
|
(10) |
The result shows that WTP behaves differently depending on the characteristics of the spatial good. This result depends on the form of the Cobb-Douglas utility function (Equation (4)), which assumes a substitution effect between different characteristics of spatial quality (proximity to the CBD and environmental amenities). So, a buyer's WTP grows as preferences for proximity to the CBD increases if the proximity value of the good is higher than the amenity value of the good (P>A). In other words, as a buyer's preference for proximity increases, her willingness to pay for goods that provide more proximity than amenities increases, meaning that she will bid higher for a property closer to the CBD.
|
|
(11) |
The derivative is negative because the expression (-Dmax-1+D) is always negative. This means that WTP decreases with distance to the CBD. Thus, it mimics the downward-sloping bid-rent function from the monocentric urban model.
|
|
(12) |
Demand for housing decreases as b increases. Since the prices for non-housing goods increase while income remains constant, then the share of budget for housing decreases because of the additional expenses for non-housing goods. With the decrease in money available for housing, the WTP for housing also decreases.
| # | Experiments compared | Metrics | t value | df | p value | Confidence interval | Comment | |
| 1 | Exp1 vs Exp2 | Individual utility | -7.852 | 29897 | 0 | -1.492 | -0.755 | significant |
| Bid price | -7.442 | 29796 | 0 | -8.406 | -4.083 | significant | ||
| Transaction price | -7.442 | 29796 | 0 | -4.203 | -2.042 | significant | ||
| 2 | Exp1 vs Exp3 | Bid price | -9.212 | 29441 | 0 | -10.587 | -5.96 | significant |
| Transaction price | -9.212 | 29441 | 0 | -5.293 | -2.98 | significant | ||
| 3 | Exp3 vs Exp4 | Bid price | -3.093 | 31015 | 0.002 | -5.174 | -0.472 | significant |
| Transaction price | -3.093 | 31015 | 0.002 | -2.587 | -0.236 | significant | ||
| 4 | Exp1 vs Exp5 | Ask price | 349.698 | 16589 | 0 | 19.401 | 19.689 | significant |
| Transaction price | 43.74 | 30522 | 0 | 19.304 | 21.72 | significant | ||
| 5 | Exp5 vs Exp6 | Ask price | 33.038 | 33011 | 0 | 2.498 | 2.92 | significant |
| Transaction price | 2.721 | 33175 | 0.007 | 0.072 | 2.622 | significant | ||
2 This UML diagram shows that classes "Buyer" and "Seller" inherit from "Traders". In the actual NetLogo code inheritance is not presented exactly as in the tradition of the object-oriented programming. In particular, to differentiate among buyers and sellers we do not create "breeds" of different traders. We rather introduce a Boolean attribute "buyer?" and "seller?" whose value can change during the model run. This feature is used in the extended version of ALMA model, where buyers who have acquired some property in the previous time steps might decide to move because of the changed neighborhood structure. Thus, they need to become sellers. In ALMA-v1.0 this procedure is not activated. So, buyers and sellers agents actually can be viewed as separate classes with one parent class.
3 Traditionally the demand curve shows the relationship between price and quantity demanded. In our case it is assumed that an individual wants to buy only 1 unit of housing. However, because each spatial good is of different quality, then an individual actually makes choice of how much quality to buy at a certain price. The amount of quality that the good provides to the individual is measured by utility she obtains from its consumption.
4 This function is known as a Michaelis-Menten function in kinetics or Monod function in biology.
5 The assumption of limited information will be relaxed in a future version of the model in order to explore its implications. The computational capabilities of Netlogo prevent us, for this version of the model, from having agents sample from all affordable parcels. However, sensitivity analysis indicates that model results are not highly sensitive to the number of parcels sampled. We attribute this result to the uniform spatial amenities imposed on this model.
6 We are aware that in real world a transaction may happen even if a bid price is lower than an ask price (sellers may accept lower bid price if for example the property has been on the market for a long time or if they anticipate that prices will fall further). However, implementation of such type of algorithms is left for the future work.
7 The graph shows the comparison of estimated rent gradients of two representative runs of Exp1 and Exp2
8 The graph shows the comparison of estimated rent gradients of two representative runs of Exp1, Exp3 and Exp4
9 The graph shows the comparison of estimated rent gradients of two representative runs of Exp1, Exp5 and Exp6
ANAS, A., R. Arnott and K. A. Small (1998). "Urban Spatial Structure." Journal of Economic Literature 36(3): 1426-1464.
ARTHUR, B. (2006). Out-Of-Equilibrium Economics and Agent-Based Modeling. Handbook of Computational Economics Volume 2: Agent-Based Computational Economics K. L. Judd and L. Tesfatsion, Elsevier B.V.: 1551-1564.
ARTHUR, W. B., S. N. Durlauf, and D. Lane (1997). The economy as an evolving complex system II. Santa Fe Institute Studies in the Science of Complexity, Vol. XXVII, Addison-Wesley.
AXTELL, R. (2005). "The complexity of exchange." Economic Journal 115(504): F193-F210.
BALMANN, A. and K. Happe (2000). Applying Parallel Genetic Algorithms to Economic Problems: The Case of Agricultural Land Markets. Microbehavior and Macroresults, IIFET 2000 Proceedings, Corvallis, Oregon USA.
BERGER, T. (2001). "Agent-based spatial models applied to agriculture: A simulation tool for technology diffusion, resource use changes, and policy analysis." Agricultural Economics 25(2-3): 245-260.
BROCK, W. A. and S. N. Durlauf (2005). Social interactions and macroeconomics. Working Paper. Madison, WI, University of Winsconsin: 28.
BROWN, D. G. and D. T. Robinson (2006). "Effects of heterogeneity in residential preferences on an agent-based model of urban sprawl." Ecology and Society 11(1): -.
CLARK, W. A. V. and F. J. Van Lierop (1986). Residential mobility and household location modeling. Handbook of Regional and Urban Economics. P. Nijkamp, Elsevier Science Publishers. Volume I.
EPSTEIN, J. M. and R. Axtell (1996). Growing Articial Societies: Social Science from the Bottom Up. Washington, DC, Brookings and Cambridge, MA, The MIT Press.
FILATOVA, T., D. C. Parker, and A. van der Veen (2007). Agent-Based Land Markets: Heterogeneous Agents, Land Prices and Urban Land Use Change. Proceedings of the 4th Conference of the European Social Simulation Association (ESSA'07), Toulouse, France.
FILATOVA, T., A. van der Veen, and D. C. Parker (2007). Modeling of a residential land market with a spatially explicit agent-based land market model (ALMA). Second Workshop of a Special Interest Group on Market Dynamics "Agent-based models of market dynamics and consumer behaviour", Groningen, The Netherlands.
FILATOVA, T. and A. van der Veen (2007). Scales in coastal land use: policy and individual decision-making (an economic perspective). Issues in Global Water System Research. Global Assessments: Bridging Scales and Linking to Policy. C. v. Bers, D. Petry and C. Pahl-Wostl. Bonn, The Global Water System Project. #2: 61-68.
FUJITA, M. and J.-F. Thisse (2002). Economics of agglomeration. Cities, industrial location and regional growth, Cambridge University Press.
GREVERS, W. A. J. and A. van der Veen (2008). Serious games for economists. Complexity and Artificial markets. K. Schredelseker and F. Hauser. Heidelberg, Springer. 614: 159-164.
HAPPE, K. (2004). "Agricultural policies and farm structures - Agent-based modelling and application to EU-policy reform." IAMO Studies on the Agricultural and Food Sector in Central and Eastern Europe 30.
IRWIN, E. G. and N. E. Bockstael (2002). "Interacting Agents, Spatial Externalities and the Evolution of Residential Land Use Patterns." Journal of Economic Geography 2: 31-54.
KIRMAN, A. P. (1992). "Whom or what does the representative individual represent?" Journal of Economic Perspectives 6(2): 117-136.
KIRMAN, A. P. and N. J. Vriend (2001). "Evolving Market Structure: An ACE Model of Price Dispersion and Loyalty." Journal of Economic Dynamics and Control 25: 459-502.
LEBARON, B. (2001). "Empirical regularities from interacting long- and short-memory investors in an agent-based stock market." IEEE Transactions on Evolutionary Computation 5(5): 442-455.
LEBARON, B. (2006). Agent-Based Computational Finance. Handbook of Computational Economics Volume 2: Agent-Based Computational Economics K. L. Judd and L. Tesfatsion, Elsevier B.V.: 1187-1233.
MANSKI, C. F. (2000). "Economic analysis of social interactions." Journal of Economic Perspectives 14(3): 115-136.
MILLER, E., J. D. Hunt, J. E. Abraham and P. A. Salvini (2004). "Microsimulating urban systems." Computers, Environment, and Urban Systems 28: 9-44.
MIYAKE, M. (2003). "Precise Computation of a Competitive Equilibrium of the Discrete Land Market Model." Regional Science and Urban Economics 33: 721-743.
NICOLAISEN, J., V. Petrov, and L. Tesfatsion (2001). "Market power and efficiency in a computational electricity market with discriminatory double-auction pricing." IEEE Transactions on Evolutionary Computation 5(5): 504-523.
OTTER, H. S., A. van der Veen, and H. J. de Vriend (2001). "ABLOoM: Location behaviour, spatial patterns, and agent-based modeling." Journal of Artificial Societies and Social Simulation 4(4)2: http://www.soc.surrey.ac.uk/jasss/4/4/2.html.
PARKER, D., D. Brown, J. G. Polhill, S. M. Manson and P. Deadman. (2008). Illustrating a new 'conceptual design pattern' for agent-based models and land use via five case studies: the MR POTATOHEAD framework. Agent-based Modelleling in Natural Resource Management. A. L. Paredes and C. H. Iglesias. Valladolid, Spain, Universidad de Valladolid: 29-62.
PARKER, D. and T. Filatova (2008). "A theoretical design for a bilateral agent-based land market with heterogeneous economic agents." Computers, Environment, and Urban Systems 32: 454-463.
PARKER, D. C., T. Berger, and S. M. Manson (2002). Agent-Based Models of Land-Use and Land-Cover Change. . LUCC Report Series No. 6; Report and Review of an International Workshop, October 4-7, 2001, USA, University of California.
PARKER, D. C., S. M. Manson, M. A. Janssen, M. J. Hoffmann and P. Deadman (2003). "Multi-agent systems for the simulation of land-use and land-cover change: A review." Annals of the Association of American Geographers 93(2): 314-337.
PARKER, D. C. and V. Meretsky (2004). "Measuring pattern outcomes in an agent-based model of edge-effect externalities using spatial metrics." Agriculture Ecosystems & Environment 101(2-3): 233-250.
POLHILL, J. G., D. C. Parker, and N. M. Gotts (2005). Introducing Land Markets to an Agent Based Model of Land Use Change: A Design. Representing Social Reality: Pre-Proceedings of the Third Conference of the European Social Simulation Association, Koblenz, Germany, September 5-9, 2005, Verlag Dietmar Völbach.
POLHILL, J. G., D. C. Parker, and N. M. Gotts (2008). Effects of Land Markets on Competition Between Innovators and Imitators in Land Use: Results from FEARLUS-ELMM. Social Simulation Technologies: Advances and New Discoveries. C. Hernandez, K. Troitzsch and B. Edmonds.
SASAKI, Y. and P. Box (2003). "Agent-Based Verification of von Thünen's Location Theory " Journal of Artificial Societies and Social Simulation 6(2)9: https://www.jasss.org/6/2/9.html
STRASZHEIM, M. R. (1975). An Econometric Analsysis of Housing Markets. New York, Columbia University Press.
STRAZSHEIM, M. (1987). The Theory of Urban Residential Location. Handbook of Regional and Urban Economics. E. S. Mills, Elsevier Science Publishers B.V. Volume II: 717-757.
TERÁN, O., J. Alvarez, M. Ablan and M. Jaimes (2007). "Characterising Emergence of Landowners in a Forest Reserve " Journal of Artificial Societies and Social Simulation 10(3)6: https://www.jasss.org/10/3/6.html.
TESFATSION, L. (2006). Agent-Based Computational Economics: A Constructive Approach To Economic Theory. Handbook of Computational Economics Volume 2: Agent-Based Computational Economics L. Tesfatsion and K. L. Judd, Elsevier B.V.: 831-880.
TESFATSION, L. and K. L. Judd (2006). Handbook of Computational Economics Volume 2: Agent-Based Computational Economics Elsevier B.V.
VAN DER VLIST, A. J., C. Gorter, P. Nijkamp and P. Rietveld (2002). "Residential Mobility and Local Housing-Market Differences." Environment and Planning A 34: 1147 - 1164.
VARIAN, H. (1992). Microeconomic Analysis. Third Edition. New York, W.W.Norton.
WILENSKY, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University. Evanston, IL.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2009]