Floriana Gargiulo and Alberto Mazzoni (2008)
Can Extremism Guarantee Pluralism?
Journal of Artificial Societies and Social Simulation
vol. 11, no. 4 9
<https://www.jasss.org/11/4/9.html>
For information about citing this article, click here
Received: 26-Mar-2008 Accepted: 14-Jul-2008 Published: 31-Oct-2008
 Abstract
Abstract|
|
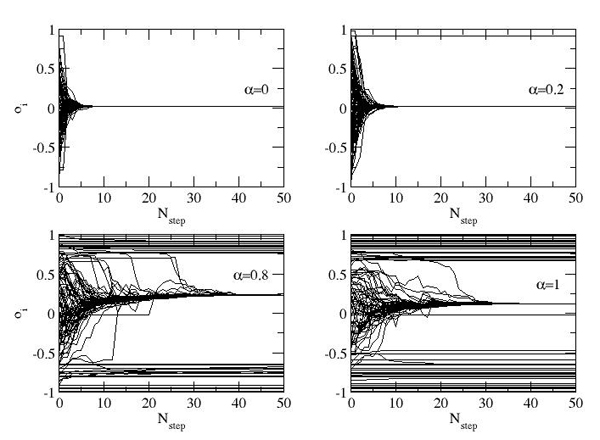
(1) |
where ki is the degree of the pre-existing agent.
|
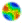
| Figure 1. Homophily in network formation. Probability of connection between the new node (N) and a node ( i) already included in the network as a function of their opinion. The left plot is realized with a parameter β=2 in Equation 1, and the right one for β=10 |
|
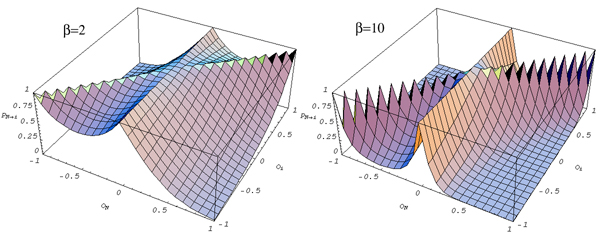
| Figure 2. Network structure. Degree distribution (left plot) and clustering coefficient as a function of the degree (right plot) for a network of 10000 nodes and for different values of β. The result is averaged over 100 realizations of the network |
|
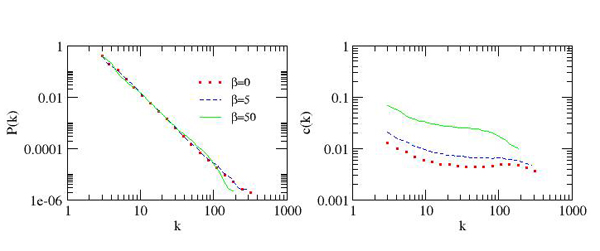
| Figure 3. Neighbours opinion at the end of network formation. The continuous line represents the average opinion of the neighbours of an agent as a function of the opinion of the agent. The three plots correspond to three different values of the parameter. The black points represent all the couples (oi, oj) for all the links of the network |
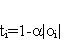
|
(2) |
|
|
(3) |
|
|
(4) |
|
| Figure 4. Results of opinion dynamics with α=0 (tolerance and interaction do not depend on opinion) on network structures built with different values of β. Each line represents the opinion evolution of one agent. Only a subset of 100 agents out of 1000 is displayed. The plot is the sketch of one realization of the simulation. Notice the difference in the x-scale of the fourth panel. |
|
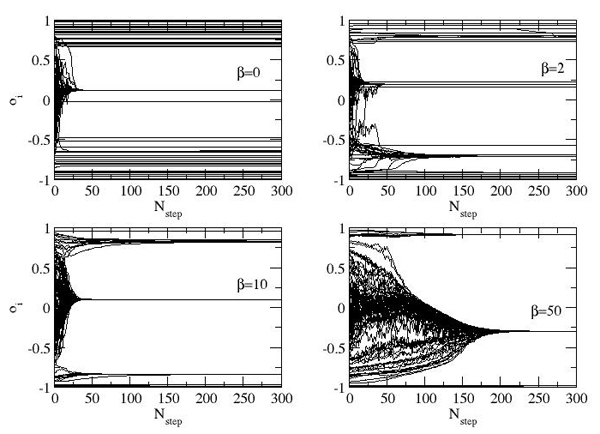
| Figure 5. Results of opinion dynamics with α=1 (tolerance and interaction strongly depend on opinion) on network structures built with different values of β. Each line represents the opinion evolution of one agent. Only a subset of 100 agents out of 1000 is displayed. The plot is the sketch of one realization of the simulation |
|
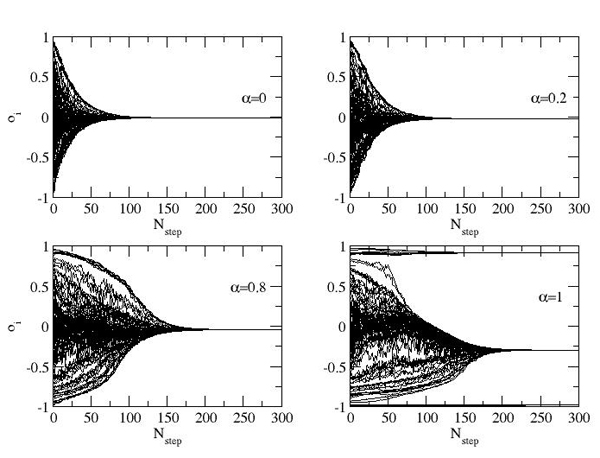
| Figure 6. Results of opinion evolution on networks built with β=0 (Barabasi Albert network) for dynamics using different values of α. Each line represents the opinion evolution of one agent. Only a subset of 100 agents out of 1000 is displayed. The plot is the sketch of one realization of the simulation |
|
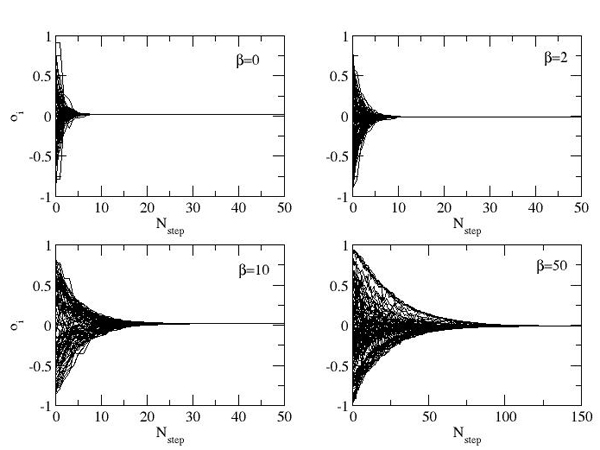
| Figure 7. Results of opinion evolution on networks built with β=50 (strong homophily) for dynamics using different values of α. Each line represents the opinion evolution of one agent. Only a subset of 100 agents out of 1000 is displayed. The plot is the sketch of one realization of the simulation |
|
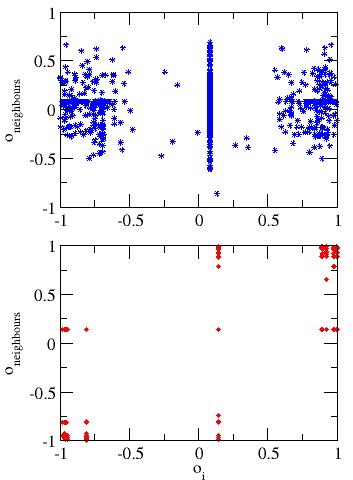
| Figure 8. Neighbours opinion at the end of the opinion dynamics process. The plots correspond to values of the parameter &beta = 0 (top) and 10 (bottom). The points represent all the couples (oi,o) for all the links of the network |
| gdim=(nag in the giant cluster) / Nag |
|
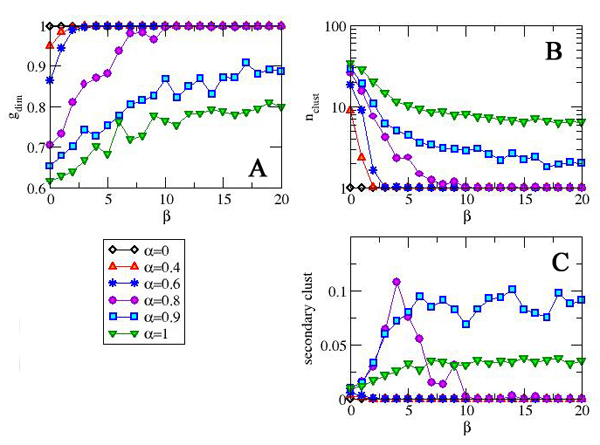
| Figure 9. Cluster statistics for different values of α as a function of the static parameter β. Relative size of the giant cluster (A), number of clusters (B) and average secondary cluster size (C). Results are averaged over 100 simulations |
|
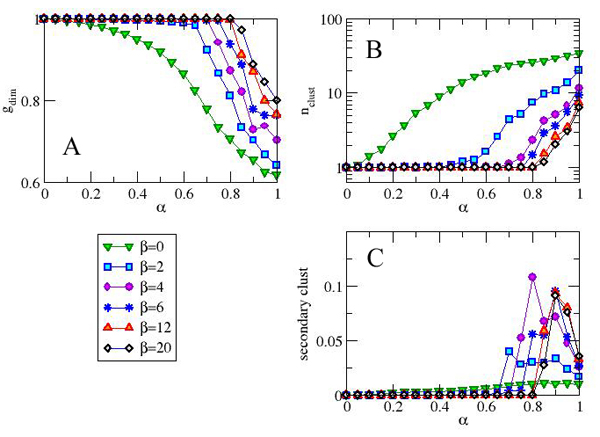
| Figure 10. Cluster statistics for different values of β as a function of the dynamical parameter α. Giant cluster dimension (A), number of clusters (B) and extremist cluster dimension (C). Results are averaged over 100 simulations |
|
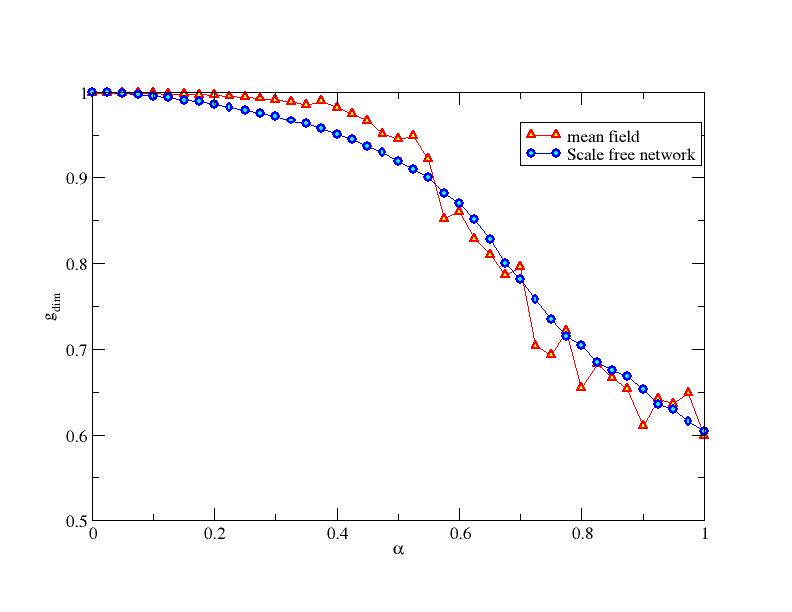
| Figure 11. Giant cluster dimension vs α for a complete graph and an opinion dependent scale free structure with β=0. Each point is obtained as the average of 100 simulations with 1000 agents |
|
|
(5) |
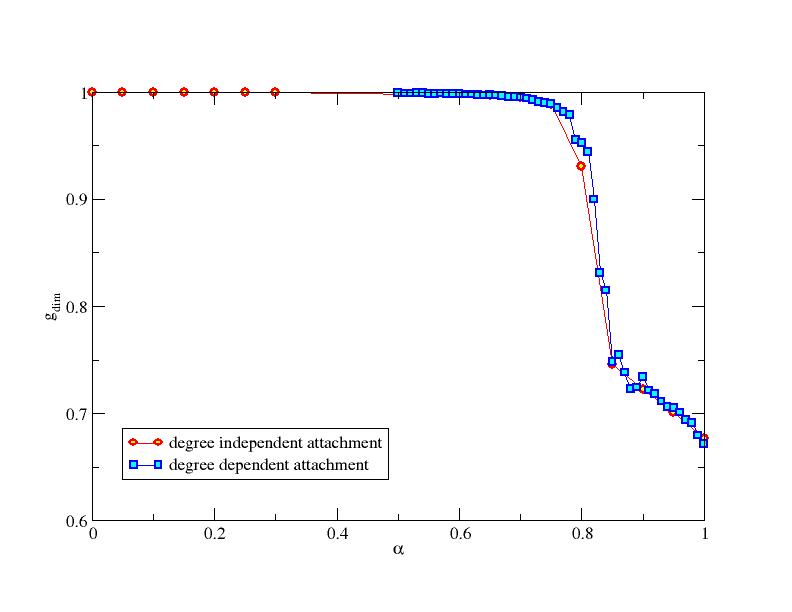
As observed in figure 12, also in this case a very good superposition is observed.
|
| Figure 12. Giant cluster dimension vs α for an opinion dependent scale free structure and an opinion dependent random degree structure, both with β=3. Each point is obtained as the average of 100 simulations with 1000 agents |
|
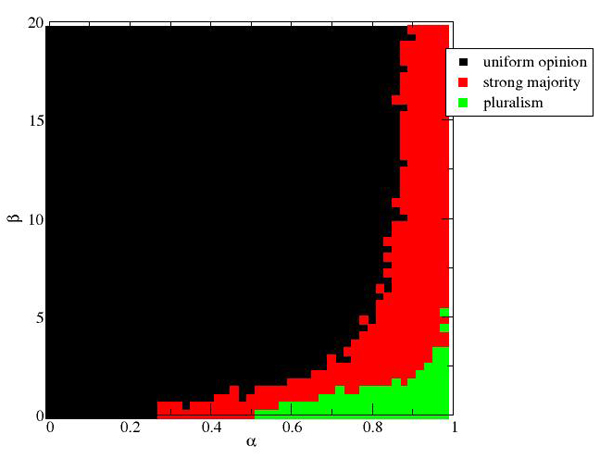
| Figure 13. Different regimes identified by number of clusters as a function of (α,β). Each point is obtained as the average of 25 simulations with 1000 agents |
AXELROD R. (1997) The Dissemination of Culture: A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution, 41. pp. 203-226.
BARABASI A.L. and ALBERT R. (1999) Emergence of Scaling in Random Networks. Science, 286. pp. 509.
BIANCONI G. and BARABASI A.L. (2001) Competition and multiscaling in evolving networks. Europhysics Letters, 54. pp. 436-442.
CASTELLANO C., FORTUNATO S. and LORETO V. (2007) Statistical physics of social dynamics. eprint arXiv: 0710.3256v1
CENTOLA D., GONZALEZ-AVELLA J.C., EGUILUZ V.M. and SAN MIGUEL M. (2007) Homophily, Cultural Drift, and the Co-Evolution of Cultural Groups. Journal of Conflict Resolution, 51. pp. 905.
CLARK R.D. and MAASS A. (1988) The role of social categorization and perceived source credibility in minority influence. European Journal of Social Psychology, 18. pp. 381-394.
CLARK R.D. and MAASS A. (1988) Social categorization in minority influence: The case of homosexuality. European Journal of Social Psychology, 18. pp. 347-364.
CLIFFORD P. and SUDBURY A. (2003) A model for spatial conflict. Biometrika, 60. pp. 581-588.
DEFFUANT G. (2006) Comparing Extremism Propagation Patterns in Continuous Opinion Models. Journal of Artificial Societies and Social Simulation, 9 (3) 8. https://www.jasss.org/9/3/8.html.
DEFFUANT G., AMBLARD F., WEISBUCH G. and FAURE T. (2002) How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5 (4) 1. https://www.jasss.org/9/3/8.html.
DEFFUANT G., NEAU D., AMBLARD F. and WEISBUCH G. (2000) Mixing beliefs among interacting agents. Advances in Complex Systems, 3. pp. 87-98.
FORTUNATO S. (2004) Universality of the Threshold for Complete Consensus for the Opinion Dynamics of Deffuant et al. International Journal of Modern Physics C, 15. pp. 1301-1307.
FORTUNATO S. and BARTHELEMY M. (2007) Resolution limit in community detection. Proceedings of the National Academy of Sciences, 104. pp. 36.
GALAM S. (2005) Heterogeneous beliefs, segregation, and extremism in the making of public opinions. Physical Review E, 71. pp. 46123.
GALAM S. and JACOBS F. (2007) The role of inflexible minorities in the breaking of democratic opinion dynamics. Physica A: Statistical Mechanics and its Applications, 381. pp. 366-376.
GOLDING P. and HARRIS P. (1997) Beyond Cultural Imperialism: Globalization. Communication and the New International Order, London: Sage
HOLLEY R.A. and LIGGETT T.M. (1975) Ergodic Theorems for Weakly Interacting Infinite Systems and the Voter Model. The Annals of Probability, 3. pp. 643-663.
JENKINS H. and THORBURN D. (2003) Democracy and New Media. MIT Press
KANDEL D.B. (1978) Homophily, Selection, and Socialization in Adolescent Friendships. American Journal of Sociology, 84. pp. 427-436.
KOZMA B. and BARRAT A. (2007) Adaptive networks: the example of consensus formation. American Physical Society, APS March Meeting, March 5-9, 2007, abstract, 22. pp. 010.
KOZMA B. and BARRAT A. (2008) Consensus formation on adaptive networks. Physical Review E, 77. pp. 16102.
MAASS A. and CLARK R.O. (1984) Hidden impact of minorities. Psychological Bulletin, 95. pp. 428-450.
MCPHERSON M., SMITH-LOVIN L. and COOK J.M. (2001) Birds of a Feather: Homophily in Social Networks. Annual Review of Sociology, 27. pp. 415-444.
MOSCOVICI S. (1980) Toward a theory of conversion behavior. Advances in experimental social psychology, 13. pp. 209-239.
MOSCOVICI S. (1985) Social influence and conformity. Handbook of social psychology, 2. pp. 347-412.
MOSCOVICI S., LAGE E. and NAFFRECHOUX M. (1969) Influence of a consistent minority on the responses of a majority in a color perception task. Sociometry, 32. pp. 365-380.
NEMETH C. and WACHTLER J. (1973) Consistency and modification of judgment. Journal of Experimental Social Psychology, 9. pp. 65-79.
NEWMAN M.E.J. and GIRVAN M. (2004) Finding and evaluating community structure in networks. Physical Review E, 69. pp. 26113.
SCHELLING T.C. (1969) Models of Segregation. American Economic Review, 59. pp. 488-493.
SCHELLING T. (1971) Dynamic models of segregation. Journal of Mathematical Sociology, 1. pp. 143-186.
STAUFFER D. and MEYER-ORTMANNS H. (2004) Simulation of Consensus Model of Deffuant et al. on a BARABSI-ALBERT Network. International Journal of Modern Physics C, 15. pp. 241-246.
STAUFFER D. and SOLOMON S. (2007) Ising, Schelling and self-organising segregation. European Physical Journal B-Condensed Matter and Complex Systems, 57. pp. 473-479.
TURNER J.C., BROWN R.J. and TAJFEL H. (1979) Social comparison and group interest in ingroup favouritism. European Journal of Social Psychology, 9. pp. 187-204.
WEISBUCH G., DEFFUANT G., AMBLARD F. and NADAL J.P. (2002) Meet, discuss, and segregate! Complexity, 7. pp. 55-63.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]