Thomas Hills and Peter Todd (2008)
Population Heterogeneity and Individual Differences in an Assortative Agent-Based Marriage and Divorce Model (MADAM) Using Search with Relaxing Expectations
Journal of Artificial Societies and Social Simulation
vol. 11, no. 4 5
<https://www.jasss.org/11/4/5.html>
For information about citing this article, click here
Received: 16-Nov-2007 Accepted: 02-Aug-2008 Published: 31-Oct-2008
 Abstract
Abstract
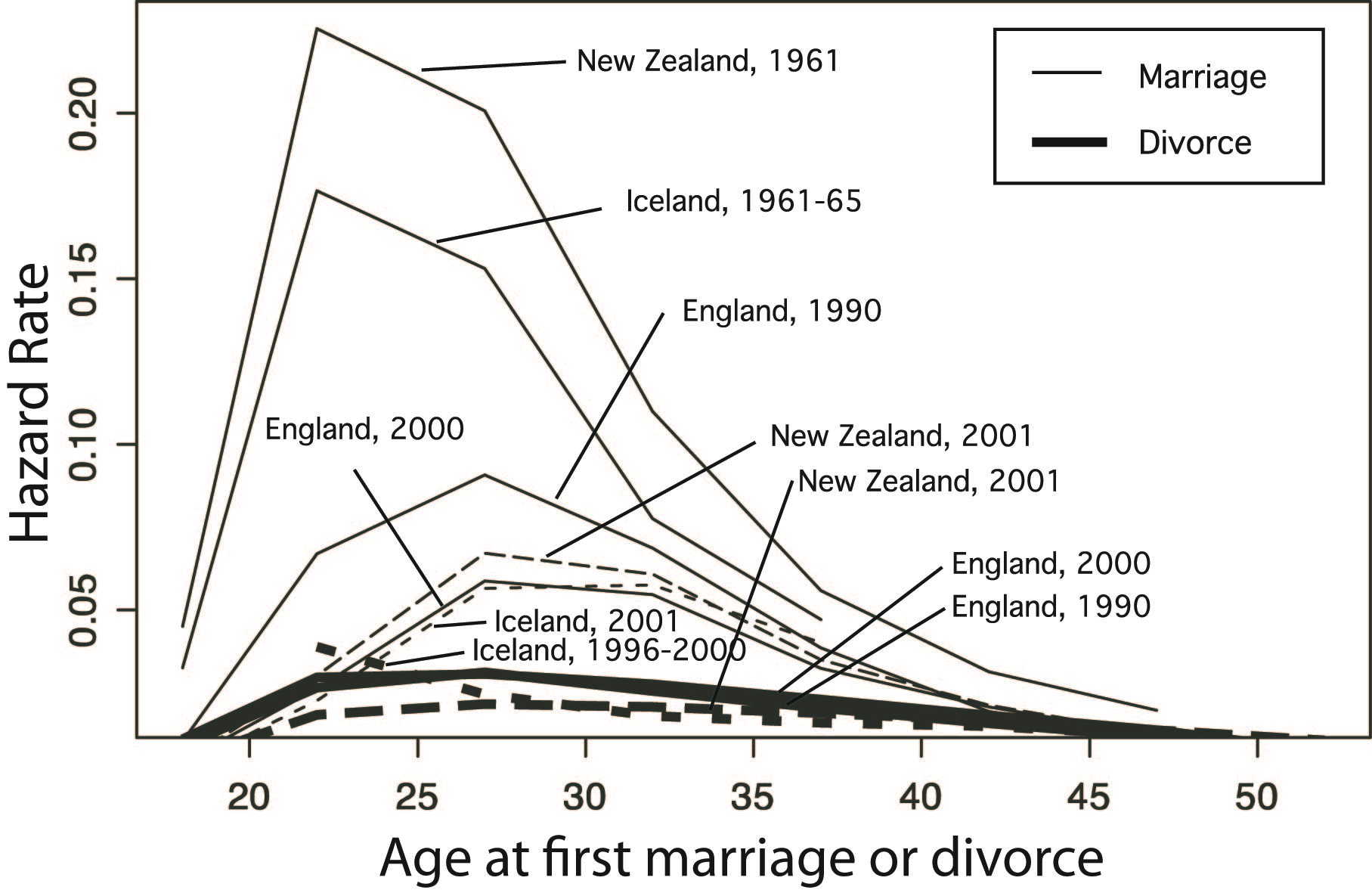 |
| Figure 1. Age at first marriage and divorce hazard rates for the United Kingdom, Iceland, and New Zealand. The curves show the mean for both sexes at a given year. Thick lines represent divorce |
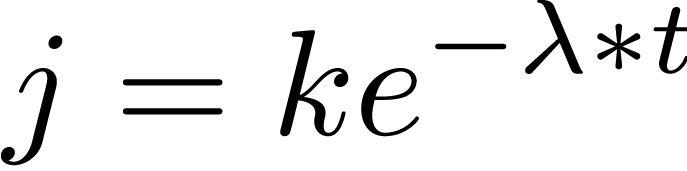
|
(1) |
|
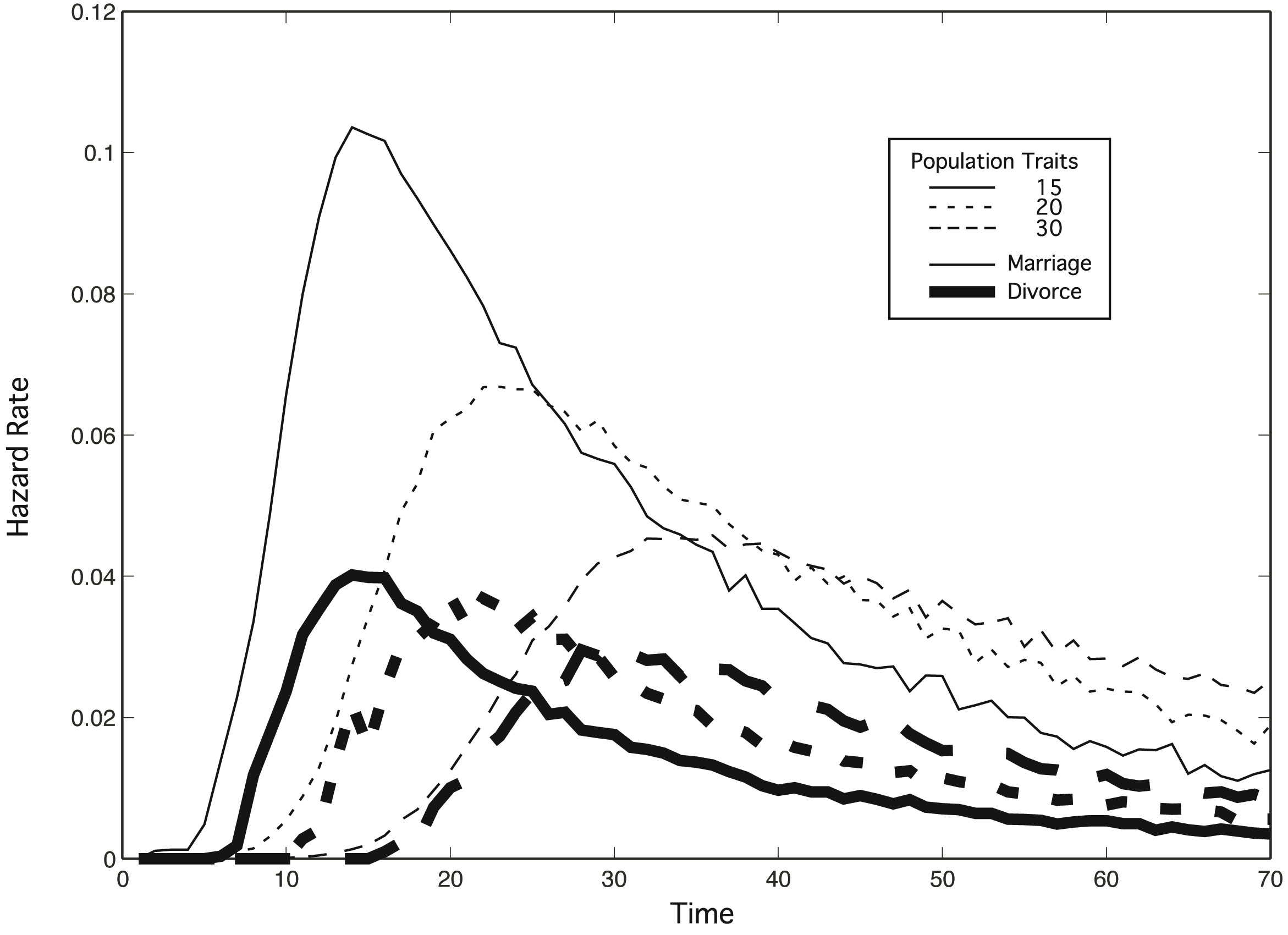
| Figure 2. Age at first marriage and divorce hazard rates for differing levels of N population traits in a population with exponential rates of relaxing expectations. Lines represent mean results for 1000 replications each of 100 males and 100 females who meet only 4 individuals of the opposite sex per year. Individuals have 10 traits (k) sampled from the number of population traits. Satisfice levels start at 10 and are exponentially relaxed according to each individual's relaxation rate, λ, sampled from the normal distribution N(0.02, 0.01). Thin lines represent hazard rates for marriage; thick lines for divorce. Time is measured in model years from the onset of reproductive age (approximately 10) |
|
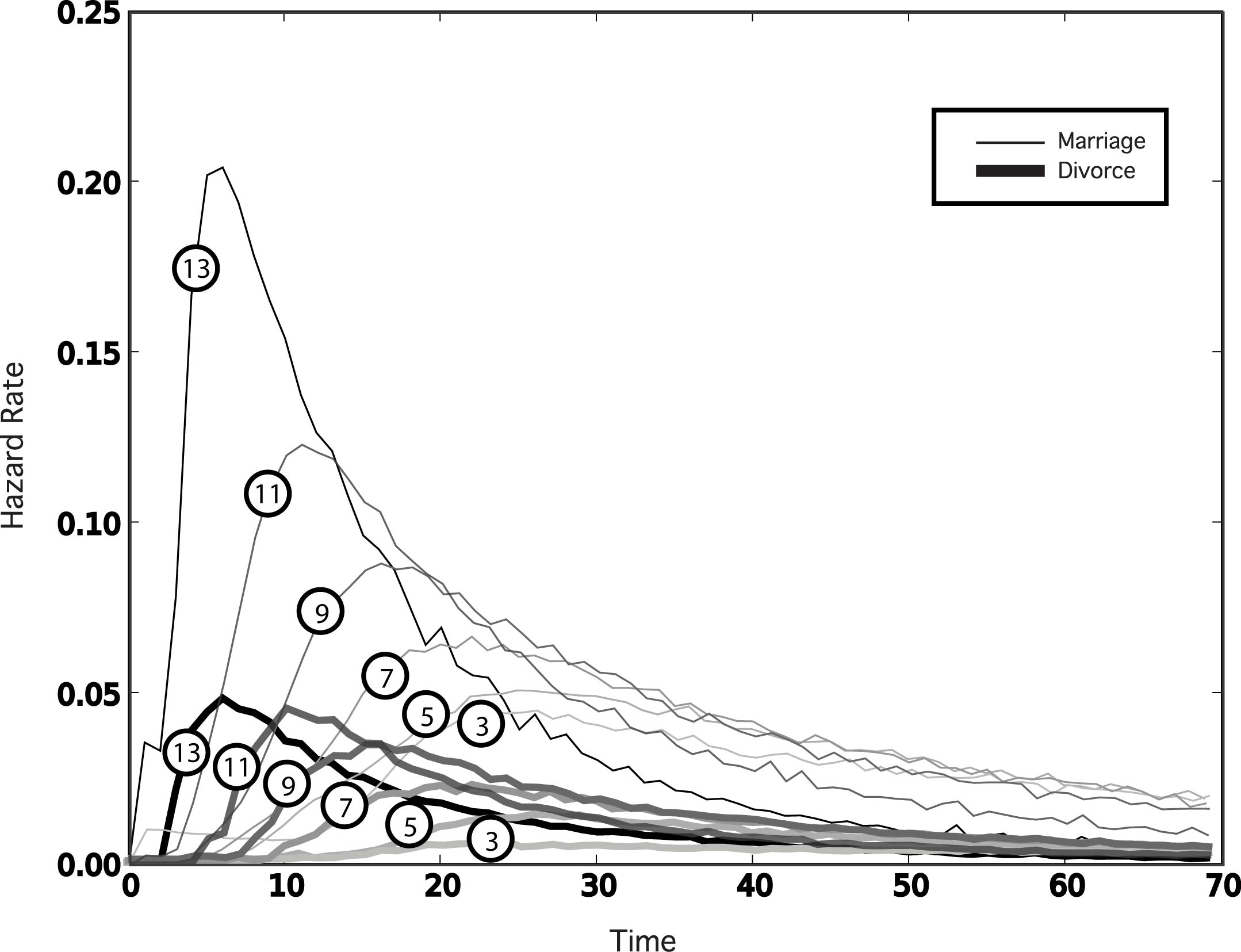
| Figure 3. Age at first marriage and divorce hazard rates for differing levels of k individual traits (indicated in circles; thin upper lines represent marriage, thicker lower lines represent divorce), with N = 15. Satisfice levels start at j = k. Otherwise the simulation parameters are as in Figure 2. As the number of individual traits k are reduced relative to the number N of traits in the population, the peak age at first marriage and peak divorce rate move to older ages |
|
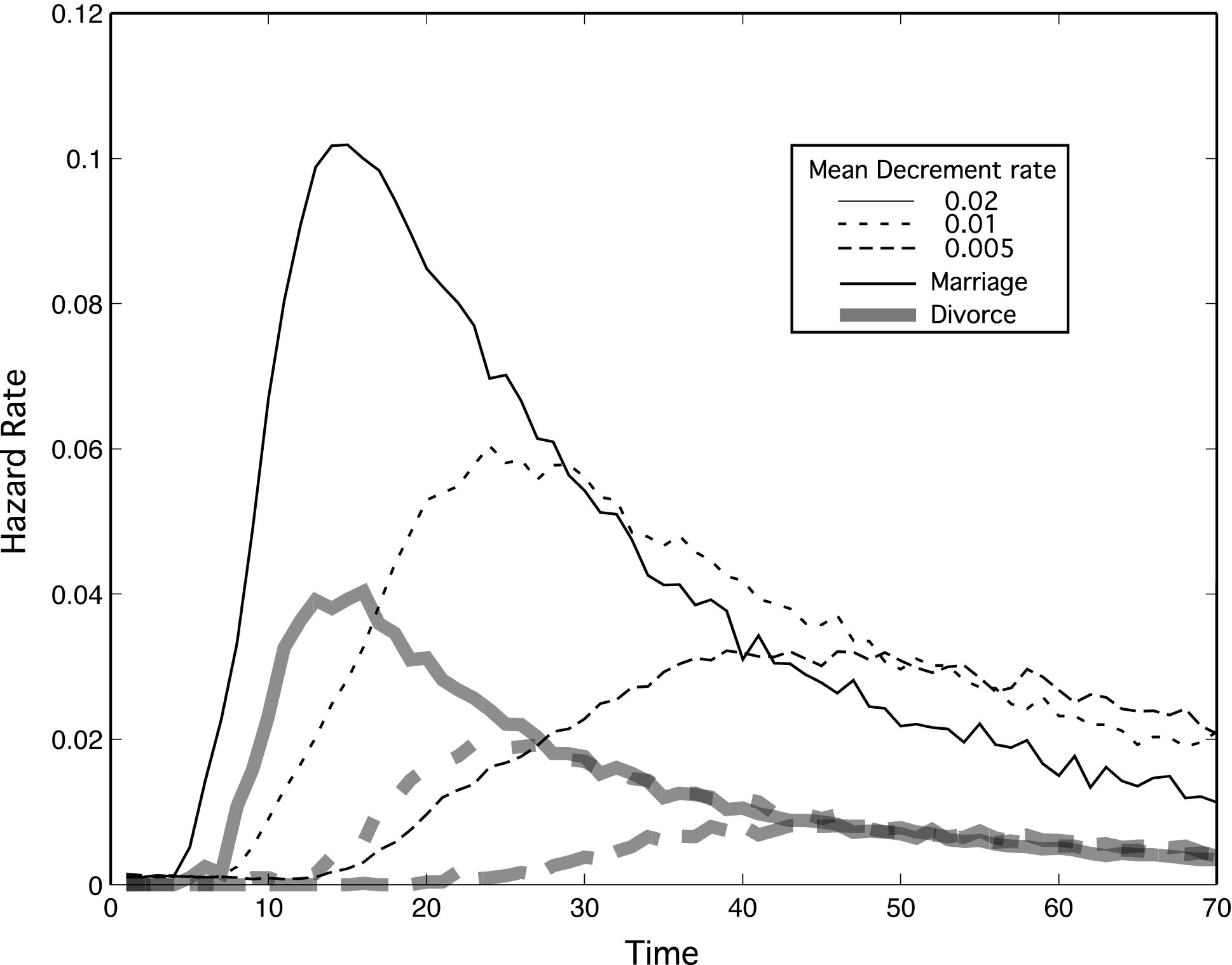
| Figure 4. Marriage and divorce hazard rates for differing mean rates of relaxing expectations (μ). σ = μ / 2. Otherwise parameters are as in Figure 2, with N = 15 and k = 10. As individuals become pickier and relax their expectations more slowly, marriage rates go down in tandem with divorce rates |
|
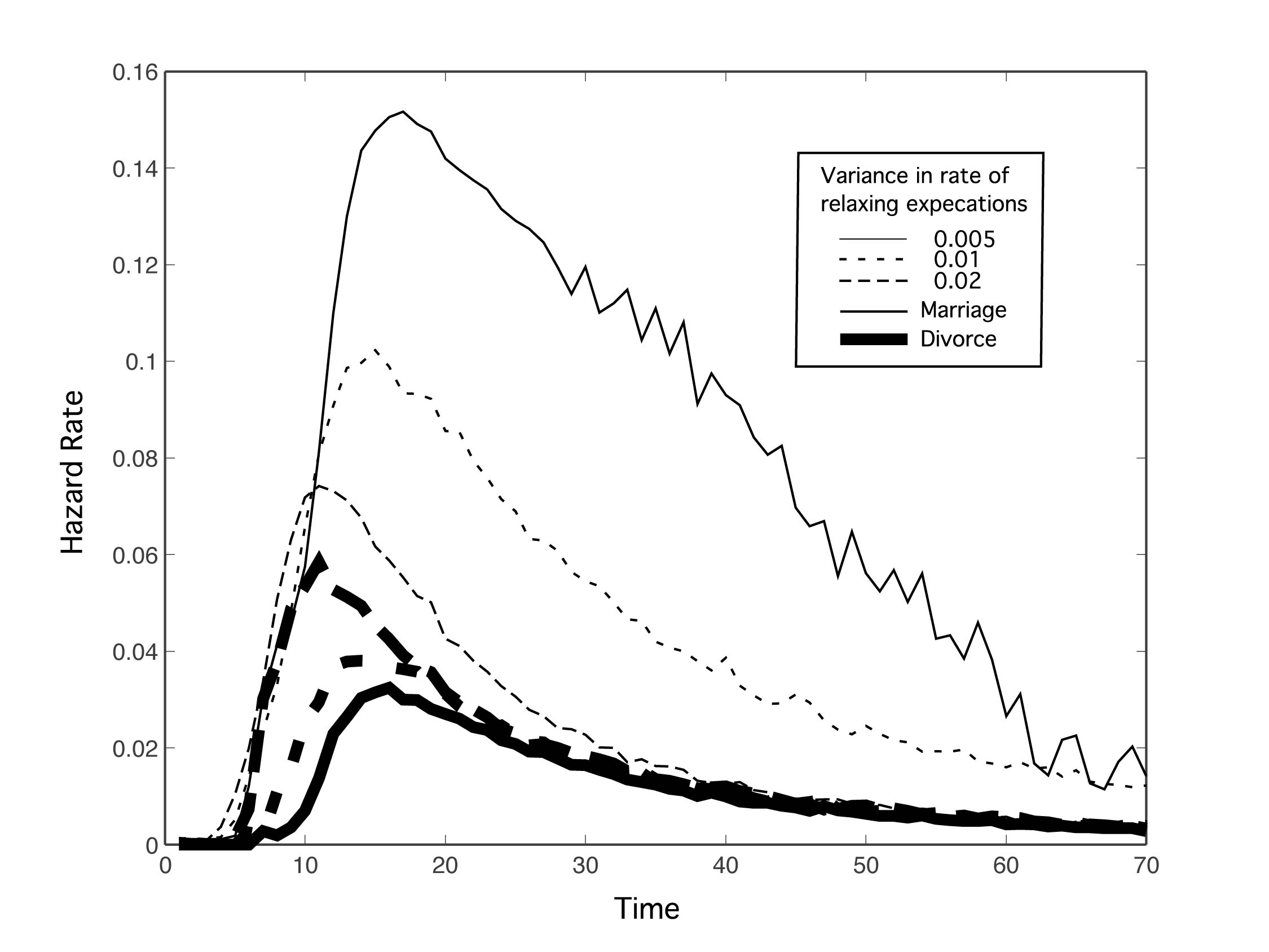
| Figure 5. Marriage and divorce hazard rates for different amounts of variance (σ) in the population's rate of relaxing expectations. μ = 0.02, N = 15, and k = 10. Otherwise, parameters are as in Figure 2. As variance in the rate of relaxing expectations increases, marriage rates go down and divorce rates go up. Also notice that age at first marriage is reduced on average with increasing variance |
AMATO, P. R. 2000 The consequences of divorce for adults and children. Journal of Marriage and the Family 62, 1269-1287.
AMATO, P. R. & Previti, D. 2003 People's reasons for divorcing. Journal of Family Issues 24, 602-626.
BELL, W. J. 1991 Searching behavior: The behavioral ecology of finding resources. New York: Chapman & Hall.
BYRNE, D. 1997 An overview (and underview) of research and theory within the attraction paradigm. Journal of Social and Personal Relationships, 14, 417-31.
BUMPASS, L. & Hsien-Hen, L. 2000 Trends in cohabitation and implications for children's family contexts in the United States. Population Studies 54, 29-41.
BUSTON, P. M. & Emlen, S. T. 2003 Cognitive processes underlying human mate choice: The relationship between self-perception and mate preference in Western society. Proc Natl Acad Sci U S A 100, 8805-10.
CHERLIN, A. J. 1992 Marriage, Divorce, Remarriage. Cambridge, MA: Harvard University Press.
COHEN, J. 1977 Sources of peer group homogeneity. Sociology of Education 50, 227-41.
CUNNINGHAM, M. R., Roberts, A. R., Wu, C., Barbee, A. P. & Druen, P. B. 1995 Their ideas of beauty are, on the whole, the same as ours: consistency and variability in the cross-cultural perception of female physical attractiveness. Journal of Personality and Social Psychology 68, 261-279.
FISCHER, C. S. 1977 Networks and Places: Social Relations in the Urban Setting. Chicago: University of Chicago Press.
FOSTER, J. D., Campbell, W. K. & Twenge, J. M. 2003 Individual differences in narcissism: inflated self-views across the lifespan and around the world. Journal of Research in Personality 37, 469-468.
GARDNER, J. & Oswald, A. 2004 How is mortality affected by money, marriage, and stress? Journal of Health Economics 23, 1181-1207.
GOODE, W. 1993 World Changes in Divorce Patterns. New Haven: Yale University Press.
HEATON, T. B., Cammack, M. & Young, L. 2001 Why is the divorce rate declining in Indonesia? Journal of Marriage and the Family 63, 480-490.
HILLS, T. 2006 Animal foraging and the evolution of goal-directed cognition. Cognitive Science 30, 3-41.
HILLS, T., Brockie, P. J. & Maricq, A. V. 2004 Dopamine and glutamate control area-restricted search behavior in Caenorhabditis elegans. Journal of Neuroscience 24, 1217-1225.
HIRSCHMAN, C. & Teerawichitchainan, B. 2003 Cultural and socioeconomic influences on divorce during modernization: Southeast Asia, 1940s to 1960s. Population and Development Review 29, 215-253.
IBARRA, H. 1995 Race, opportunity and diversity of social circles in managerial networks. . The Academy of Management Journal 38, 673-703.
JAFFE, K. 1999 On the adaptive value of some mate selection strategies. Acta Biotheoretica 47, 29-40.
KALICK, S. M. & Hamilton, T. E. 1986 The matching hypothesis reexamined. Journal of Personality and Social Psychology 51, 673-682.
KALMIJN, M. 1998 Intermarriage and homogamy: causes, patterns, trends. Annu Rev Sociol, 395-421.
KANDEL, D. B. 1978 Homophily, selection and socializationin adolescent friendships. The American Journal of Sociology 84, 427-36.
KAREIVA, P. & Odell, G. 1987 Swarms of predators exhibit "preytaxis" if individual predators use area-restricted search. American Naturalist 130, 233-270.
KITSON, G. C., Babri, K. B. & Roach, M. J. 1985 Who divorces and why: A review. Journal of Family Issues 6, 255-293.
KREIDER, R. M. 2002 Number, timing, and duration of marriages and divorces: 1996 Current Population Reports P70-97
LINCOLN, J. R. & Miller, J. 1979 Work and friendship ties in organizations: a comparative analysis of relational networks. Administrative Science Quarterly 24, 181-199.
MARSDEN, P. V. 1988 Homogeneity in confiding relations. Social Networks 10, 57-76.
MATHEWS, T. J. & Hamilton, B. E. 2002 Mean age of mother, 1970-2002, National Vital Statistics Reports 51.
MCPHERSON, M., Smith-Lovin, L. & Cook, J. M. 2001 Birds of a feather: homophily in social networks. Annual Review of Sociology 27.
MILLER, G. F. & Todd, P. M. 1998 Mate choice turns cognitive. Trends in Cognitive Sciences 2, 1990-1998.
MORELAND, R.L. and Zajonc, R.B. 1982 Exposure effects in person perception: familiarity, similarity, and attraction. Journal of Experimental Social Psychology 18, 395-415.
NATIONAL STATISTICS 2006 http://www.statistics.gov.uk. Crown copyright material is reproduced with the permission of the Controller of HMSO.
OCHOA, G. and Jaffe, K. 1999 On sex, mate selection and the red queen. Journal of Theoretical Biology, 199, 1-9.
PENN, D. J. & Potts, W. K. 1999 The evolution of mating preferences and major histocompatability complex genes. American Naturalist 153, 145-164.
PESKIN, M. & Newell, F. N. 2004 Familiarity breeds attraction: effects of exposure on the attractiveness of typical and distinctive faces. Perception 33, 147-157.
PUSEY, A. & Wolf, M. 1996 Inbreeding avoidance in animals. Trends in Ecology and Evolution 11, 201-206.
SHRUM, W., Cheek, N. H. J. & Hunter, S. M. 1988 Friendship in school: gender and racial homophily. Sociology of Education 61, 227-239.
SRIVASTAVA, S., John, O. P., Gosling, S. D. & Potter, J. 2003 Development of personality in early and middle adulthood: set like plaster or persistent change? Journal of Personality and Social Psychology 84, 1041-1053.
STATISTICS CANADA 1996 Vital statistics compendium. Catalogue no. 84-214-XIE.
STATISTICS ICELAND 2004 Population. Statistical Series 89 (31).
STATISTICS NEW ZEALAND 2004 Demographic Trends 2003, Catalogue no. 30.001.
THORNHILL, R. & Gangestad, S. W. 1999 Facial Attractiveness. Trends in Cognitive Sciences 3, 452-460.
TODD, P. M. 1997 Searching for the next best mate. In Simulating Social Phenomena (ed. R. Conte, R. Hegselmann & P. Terna), pp. 419-436. Berlin: Springer-Verlag.
TODD, P. M., Billari, F. C. & Simão, J. 2005 Modeling the emergence of social marriage patterns produced by individual mate-search heuristics. Demography 42, 559-574.
TODD, P. M. & Miller, G. F. 1999 From pride and prejudice to persuasion: satisficing in mate search. In Simple Heuristics That Make Us Smart (ed. G. Gigerenzer & P. M. Todd), pp. 287-308. Oxford: Oxford University Press.
TREGENZA, T. & Wedell, N. 2000 Genetic compatibility, mate choice and patterns of parentage: invited review. Molecular Ecology 9, 1013-27.
U.S. CENSUS BUREAU 2003 Annual Social and Economic Supplement: 2003 Current Population Survey, Series P20-553.
WRIGHT, E. O. 1997 Class counts: Comparative studies in class analysis. New York: Cambridge University Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]