James Millington, Raúl Romero-Calcerrada, John Wainwright and George Perry (2008)
An Agent-Based Model of Mediterranean Agricultural Land-Use/Cover Change for Examining Wildfire Risk
Journal of Artificial Societies and Social Simulation
vol. 11, no. 4 4
<https://www.jasss.org/11/4/4.html>
For information about citing this article, click here
Received: 30-Sep-2007 Accepted: 10-Jul-2008 Published: 31-Oct-2008
 Abstract
Abstract

|
| Figure 1. The fragmented and heterogeneous spatial structure of a traditional Mediterranean agricultural landscape. The aerial photograph from the study area spans approximately 1.6 km (1 mile) and contains numerous land-use and cover types including pasture, crops and urban areas. |
|
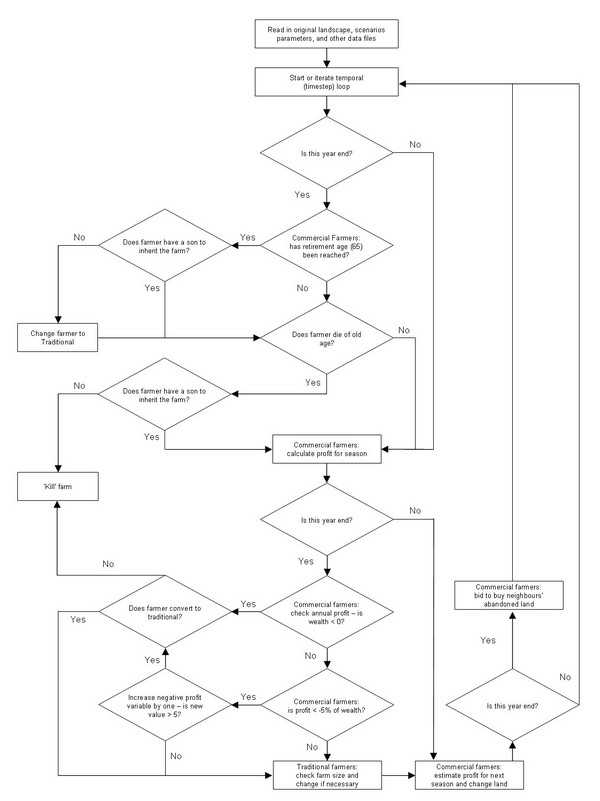
| Figure 2. Procedure of the agent-based model of land-use decision-making. During each time-step seasonal functions are executed; annual functions are executed every fourth time-step (i.e., four seasons are simulated per year). |
"Whoever has a vineyard nowadays is like a gardener... they like to keep it, even if they lose money. They maintain vineyards because they have done it all their life and they like it, even having to pay for it. If owners were looking for profitability there would be not a single vineyard... People here grow wine because of a matter of feeling, love for the land..."
"Part-time workers? Yes, most of them... Here there are only retired people and their children, who work somewhere else, and help their retired parents with the labouring. There is no way to live on wine production."
"There are some young farmers, 5 or 6 of whom are less than 25 years old, that are making important investments. If someone wants to live from livestock farming, they need to have an entrepreneurial vision, a business mentality, like in any company."Such farmers will adopt those land-use and farming practices that maximise their income. Different behaviours (i.e., model rules) are therefore required to characterise 'commercial' versus 'traditional' agents (Table 1). Attributes and decision-making rules common to both agent types are now described (see Table 2 for list of all attributes and parameters). Subsequently, attributes and rules unique to each agent type are discussed in detail.
| Table 1: Comparison of attributes of 'traditional' and 'commercial' agents. Attributes were derived after interviews with local actors within the study area. | ||
| Attribute | Traditional Agent | Commercial Agent |
| Commitment | 'Part-time' or 'Hobby' farmer | 'Full-time' businessman |
| Age | Any, greater than 19 years | Maximum 65 years (retirement age) |
| Land Exchange | Will not exchange land | Will buy/sell land to achieve profit |
| Land Uses | Maintains land in 'traditional' uses | Whatever land use maximises profit |
| Financial Attitude | Profit is not primary determinant of behaviour | Aims to maximise profit |
| Table 2: Attributes and parameters considered in the model. Attributes and parameters are presented for agents, pixels, farms, and those that are universal within the model. Units CU are arbitrary 'Currency Units'. | |||
| Name | Unit | Range of Values | Description |
| Agent | |||
| age | Years | 20 – 100 | Agent's age |
| perspective | - | Commercial, Traditional | Agent worldview, determining behaviour |
| personal_choice | - | 0 – 1 | Propensity of an agent to become a 'commercial' farmer |
| wealth | CU | 0 – ∞ | Agent's total accumulated value |
| profit | CU | 0 – ∞ | Farm profit for this season |
| max_bid | CU | 0 – ∞ | Maximum bid an agent will offer to buy a pixel of land |
| poor_profit | CU | 0 – Length of model replicate | Number of years that annual profit has been below the poor_profit threshold |
| est_profit | CU | -∞ – ∞ | Agent's estimated profit for the next year |
| ann_profit | CU | -∞ – ∞ | Total farm profit for the current year |
| mf_size | Pixels | 0 – Area of landscape | Number of pixels agent can manage before incurring farmCost on additional pixels (age dependent) |
| est_valueC | CU | -∞ – ∞ | Estimated valueC for the next year |
| est_valueP | CU | -∞ – ∞ | Estimated valueP for the next year |
| est_costC | CU | -∞ – ∞ | Estimated costC for the next year |
| est_costP | CU | -∞ – ∞ | Estimated costP for the next year |
| est_farmCost | CU | -∞ – ∞ | Estimated farmCost for the next year |
| prev_est_valueC | CU | -∞ – ∞ | Estimated valueC for the last year |
| prev_est_valueP | CU | -∞ – ∞ | Estimated valueP for the last year |
| prev_est_costC | CU | -∞ – ∞ | Estimated costC for the last year |
| prev_est_costP | CU | -∞ – ∞ | Estimated costP for the last year |
| prev_est_farmCost | CU | -∞ – ∞ | Estimated farmCost for the last year |
| Pixel | |||
| frag_value | - | 0 – 1 | Fragmentation value indicating relative size and proximity of pixel to the rest of the farm |
| lcap | - | 0 – 2 | Land capability measure, higher values are more suitable for agricultural uses |
| state | - | Crops, Pasture, Non-Agricultural | Land use pixel is currently in |
| t_in_state | Years | 0 – Length of model replicate | Duration pixel has remain in its current state |
| set_price | CU | 0 – 10 | CU agent is willing to sell the pixel for |
| road_dist | Pixels | 0 – lsp_max | Distance to the nearest road |
| prop_farm | - | 0 – 1 | Proportion of farm that the pixel cluster (field) in which the pixel lies composes |
| Farm | |||
| max_dist | Pixels | 0 – lsp_max | Greatest distance between two pixels owned by the same agent |
| Universal | |||
| propT | - | 0 – 1 | Proportion of agents in the landscape with a 'traditional' perspective |
| propC | - | 0 – 1 | Proportion of agents in the landscape with a 'commercial' perspective |
| valueC | CU | 0 – 10 | CU accrued from one pixel of crops for one season |
| valueP | CU | 0 – 10 | CU accrued from one pixel of pasture for one season |
| costC | CU | 0 – 10 | Cost of maintaining one pixel of crops for one season |
| costP | CU | 0 – 10 | Cost of maintaining one pixel of pasture for one season |
| farmCost | CU | 0 – 10 | Cost incurred per pixel in farms greater than max_farm_size or mf_size |
| convC | CU | 0 – 1 | Cost to convert a pixel from crops to pasture |
| convP | CU | 0 – 1 | Cost to convert a pixel from pasture to crops |
| convNA | CU | 0 – 1 | Cost to convert a pixel from non-agricultural to pasture or crops |
| lsp_max | Pixels | Maximum distance possible across the landscape | |
| poor_years | Years | 0 – Length of model replicate | Number of years of profit less than or equal to loss_resilience that an agent will sustain before retiring |
| loss_resilience | % | 0 – 100 | Profit threshold used to count poor_years |
| current_market_price | CU | 0 – ∞ | mean_tot_pixel_profit _ 40 |
| max_farm_size | Pixels | 0 – Area of the landscape | Number of pixels agent can manage before incurring farmCost on additional pixels |
| mean_tot_pixel_profit | CU | -∞ – ∞ | Mean pixel profit for the season across all pixels owned by commercial agents |
| IF (U[0,1] < (propC + personal_choice) ) | (S1) |
where U[0,1] is a uniform random deviate in the interval [0,1], propC is the proportion of agents in the landscape that are commercial, and personal_choice is a parameter added to ensure that when there are no other commercial agents in the landscape there is still a chance that an heir will want to continue the business. Thus, the personal_choice parameter accounts for the personal choice of the heir and the parent's individual influence over the heir's attitudes (which are likely to be just as, if not more, important than the proportion of the local community that has the 'commercial worldview'). This value may be positive (the heir is inclined to continue the business) or negative (the heir is disinclined to continue the business). The probability of inheritance considers the proportion of commercial agents in the landscape as this is likely to be an important factor in determining whether an heir wants to continue their parent's business. If an heir inherits the farm, a new personal_choice value is set as ±10% of their parent's. The heir's age is randomly set to a value between 20 and 40, ensuring that the value is less than the dying agent's age minus 20 (assuming that farmers do not have children before the age of 20). However, if the agent is younger than 40 it is assumed that either they do not have an heir, or if they do that the heir is not old enough to assume the ownership of the farm. If there is no heir, ownership of all pixels is released (i.e., enter an un-owned state) and the farm is assumed to be abandoned.
| Table 3: Parameters for 'business as usual' model configuration. These initial conditions and parameter values specify the 'business as usual' (baseline) scenario (see Table 2 for definition of parameters). Results from this parameter set are used as the standard by which to evaluate the outcomes of the model experiments we conducted. | |
| Parameter | Value |
| Agent Age | Uniformly random deviate in the interval [20, 65] |
| Conversion Costs | Non-Agricultural, 0.3; Pasture, 0.2, Crops, 0.1; |
| Land Use | SPA 56 1999 land use (3 uses, 109 patches) |
| Loss Resilience | -5% |
| Poor Years | 5 years |
| Land Tenure | SPA 56 2005 land tenure (519 agents, 1213 patches) |
| Market Values | valueC = 5.0 valueP = 2.5, costC = 1.0, and costP=1.0 |
| Personal Choice | Uniformly random deviate in the interval [-0.5, 0.5] |
| Perspective | Randomly assigned with equal probability |
| Fragmentation Value = 1 - ( prop_farm / max_dist ) | (1) |
where prop_farm is the proportion of the total farm area composed by the pixel cluster (i.e., field) in which the pixel under consideration lies, and max_dist is the maximum distance between the pixel under consideration and another pixel owned (and in use) by the same agent. Thus, when prop_farm is large and max_dist is small, the fragmentation value of the pixel is low. This index penalises pixels in small clusters at great distances from other pixels owned by the agent. Distance to the nearest road or track is considered as a proxy for incurred transport costs. Direct distance to market is not considered as it is by von Thünen's model because there are multiple market locations for our study area. The cost of distance to the nearest road for each pixel is normalised by the maximum distance possible across the whole study area (giving a range for this value of [1/max_dist] to 1).
| Crops profit = (valueC × lcap) - (2 × frag_value × costC ) - (road_dist / lsp_max) | (2) |
| Pasture profit = (valueP × lcap) - costP - (road_dist / lsp_max) ) | (3) |
| Abandoned cost = 0.1 | (4) |
| Est_ValueC = valueC + actual_value_diffcC + U[0,0.5] × (valueC - prev_est_valueC) | (5) |
where actual_value_diffcC is the difference between the previous value of crops and the current value of crops, prev_est_valueC is the previous estimated value of crops. This method ensures agents can estimate future prices reasonably well when values and costs change slowly, but perform less well when changes are rapid.
| IF (U[0,1] < (propT + personal_choice) OR age > 50) | (S2) |
| max_bid = 4 × pixel_profit × (65 – age) | (6) |
where pixel_profit is the estimated increased profit it will afford (multiplied by four seasons to give profit for a year) and age is the age of agent. The second constant is included to account for the age of the farmer, as this gives a rough guide to the number of years of profit the pixel (if bought) will provide to the farmer until retirement. If the bid is larger than the asking price of the current owner, ownership passes to the bidding agent and land-use is changed to the most profitable state. The buying agent's wealth is decreased by the asking price (not the maximum bid), and the seller's increased commensurately. If two agents bid for the same pixel, the highest bid wins (assuming it is greater than the asking price) and the maximum bid is the value that changes hands. The asking price of an agent is set as the current wealth of that agent divided by the total number of pixels owned by that agent. If the pixel is abandoned but un-owned the asking price is set to the 'current market price':
| Current Market Price = 40 × mean_tot_pixel_profit | (7) |
where mean_tot_pixel_profit is the mean pixel profit for the season across all pixels owned by commercial agents in the landscape. The constant gives an estimate of potential profit to be made by that pixel (in the current market state) over the next decade (i.e., 40 time-steps). If a bid is not as large as the asking price, ownership stays with the current owner and the pixel remains in the abandoned state. Whatever the result of a bid, once all agents' bids have been considered, the next season then begins.
| IF (mean_tot_pixel_profit + propC - (age / 100)) > 0 | (S3) |
This statement assumes that the heir will be willing to become a commercial farmer when: (i) the profit in the landscape is generally high, (ii) there are other commercial farmers in the landscape (i.e., they see that others are finding it possible to make a living from their land), and (iii) their age is low (and therefore they are assumed to be more willing to take a risk and 'give it a go'). Age is scaled to the order of mean_tot_pixel_profit and propC.
| IF (U[0,1] < (propT + personal_choice) ) | (S4) |
| mf_size = max_farm_size × exp((65 – age)/wt)) | (8) |
where mf_size is the maximum farm size of the retired agent, age is the age of the agent in question, and wt is a shape parameter (default value = 8, chosen in rough accordance with interviewees' understanding). Thus, the area of land a farmer is able to maintain is assumed to decrease exponentially with age after retirement.

|
| Figure 3. Examples of random maps generated with varying percolation probability parameter P. Clockwise from top left, maps are generated with P = 0.2, P = 0.4, P = 0.6 and P = 0.8. The two colours represent two different (hypothetical) land covers. |
| Table 4: Parameter values for ABM/LUCC testing. Parameter values were chosen to span the parameter space of the model. This allowed us to examine the range of possible model states and investigate important parameters and input data. | ||
| Scenario | Variable | Distribution of Values |
| LU1 | Land use | P = 0.2 (SPA land-tenure, 509 LU patches) |
| LU2 | Land use | P = 0.4 (SPA land-tenure, 291 LU patches) |
| LU3 | Land use | P = 0.5 (SPA land-tenure, 198 LU patches) |
| LU4 | Land use | P = 0.6 (SPA land-tenure, 94 LU patches, predominantly pasture) |
| LU5 | Land use | P = 0.6 (SPA land-tenure, 83 LU patches, predominantly crops) |
| LU6 | Land use | P = 0.8 (SPA land-tenure, 1 pasture patch) |
| LU7 | Land use | P = 0.8 (SPA land-tenure, 1 crops patch) |
| LT1 | Land tenure | P = 0.20 (511 Agents, 2653 LT patches) |
| LT2 | Land tenure | P = 0.40 (478 Agents, 1297 LT patches) |
| LT3 | Land tenure | P = 0.45 (442 Agents, 1005 LT patches) |
| LT4 | Land tenure | P = 0.50 (404 Agents, 791 LT patches) |
| LT5 | Land tenure | P = 0.55 (313 Agents, 480 LT patches) |
| LT6 | Land tenure | P = 0.60 (224 Agents, 296 LT patches) |
| LT7 | Land tenure | P = 0.80 (19 Agents, 19 LT patches) |
|
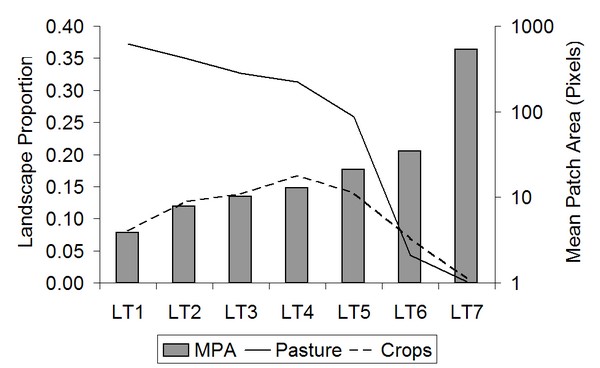
| Figure 4. Landscape land-use proportions and mean land-use patch area for random land-tenure maps. An inverse relationship between abundance of pasture (solid line) and mean patch area (bars) is evident. Abundance of crops (dashed line) peaks for median mean patch area. Scenarios are specified in Table 4 |
|
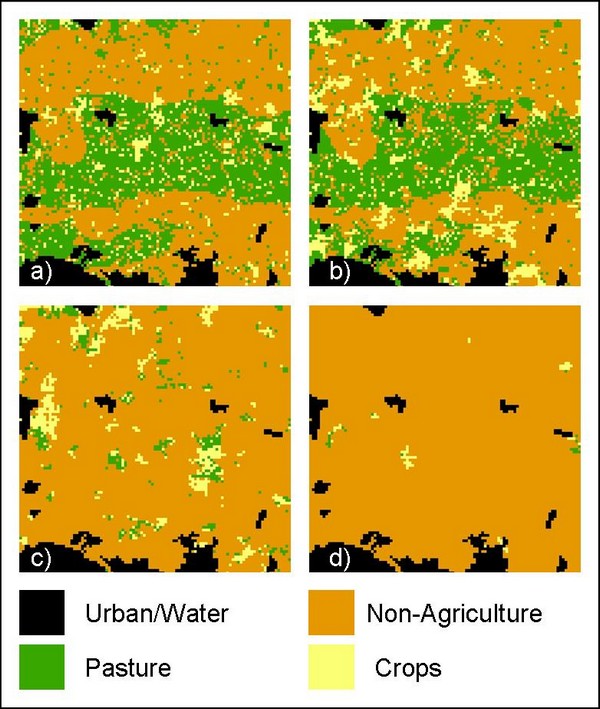
| Figure 5. Land-use maps from land-tenure scenarios. a) LT1, b) LT2, c) LT6 and d) LT7 As initial mean land-tenure parcel size increases, land area devoted to pasture decreases commensurate with increases in non-agricultural land uses. |
| Table 5: Agricultural landscape structure characteristics for land-tenure maps. Also presented are final agricultural land-use proportions for corresponding model replicates. Land-tenure maps with p ≥ 0.60 result in landscapes with very low agricultural land-use due to the large size of patches and farms | ||||||
| Initial Land Tenure | Final Agricultural* Land Use | |||||
| Scenario | Agent Parcels¶ | MPA‡ | Small Farms† | Landscape Proportion | Number of Patches | |
| Baseline | 2.34 | 8.41 | 1.00 | 0.44 | 64 | |
| LT1 | 5.18 | 3.85 | 1.00 | 0.45 | 484 | |
| LT2 | 2.78 | 7.87 | 0.96 | 0.48 | 452 | |
| LT3 | 2.27 | 10.15 | 0.87 | 0.47 | 444 | |
| LT4 | 1.96 | 12.90 | 0.76 | 0.48 | 359 | |
| LT5 | 1.53 | 21.25 | 0.43 | 0.40 | 310 | |
| LT6 | 1.32 | 34.46 | 0.21 | 0.11 | 199 | |
| LT7 | 1.00 | 536.89 | 0.01 | 0.01 | 20 | |
¶Mean number of parcels per agent
‡Mean parcel area (pixels)
†Farms with size < max_farm_size (as proportion of landscape)
*Crops plus pasture
|
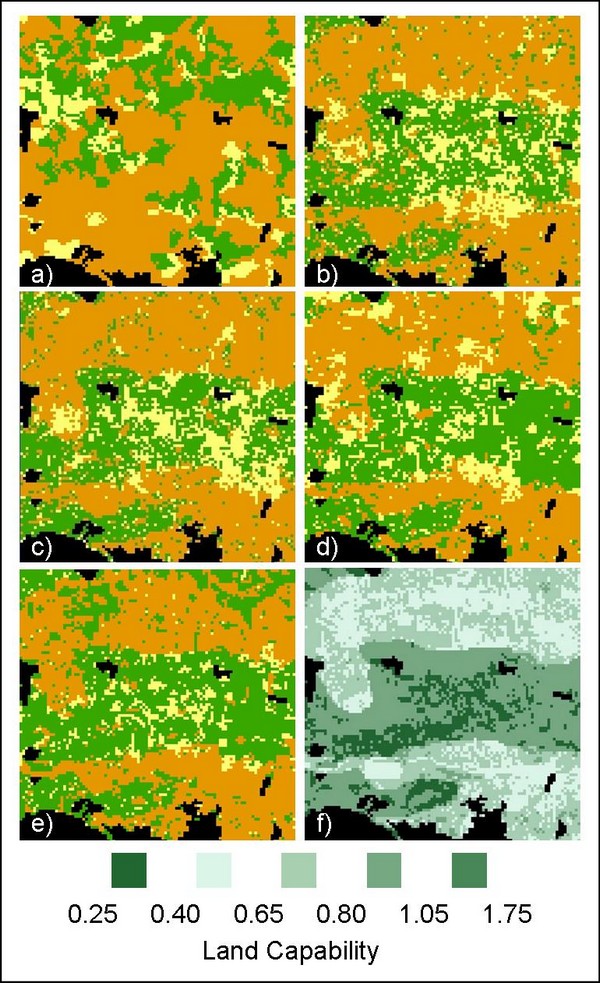
| Figure 6. Land-use maps from land-use scenarios. a) Original SPA land-use, b) LU1, c) LU2, d) LU5, e) LU7 and f) land capability. Key for land-use maps as in Figure 5. Simulated maps for model replicates of land-use scenarios (b – e) converge toward a similar configuration, related to land capability patterns (f). This land-use relationship is stronger between model maps than with the empirical map (a) |
| Table 6: Spatial metrics of land-use pattern for land-use scenarios. Spatial metrics examined are the number of patches (NP) and contagion (CONTAG). Greater numbers of patches and smaller contagion values indicate a more fragmented ('patchy') landscape. This is the case for simulation results compared with initial land-use configuration in each case. Scenarios are specified in Table 4 | |||||
| Initial | Final | ||||
| Scenario | NP | CONTAG | NP | CONTAG | |
| Baseline | 79 | 33.0 | 514 | 38.8 | |
| LU1 | 509 | 22.5 | 552 | 20.8 | |
| LU2 | 291 | 30.3 | 541 | 24.1 | |
| LU3 | 198 | 35.4 | 499 | 21.9 | |
| LU4 | 130 | 43.0 | 403 | 24.3 | |
| LU5 | 126 | 43.5 | 446 | 22.1 | |
| LU6 | 1 | 100.0 | 380 | 30.8 | |
| LU7 | 1 | 100.0 | 359 | 23.7 | |
| Table 7: Estimated wildfire risk. Mean, standard deviation, minimum and maximum values are reported for maps from each scenario and from the original, observed landscape (SPA). Generally, mean risk is greater for landscapes resulting from model scenarios. However, maximum values and standard deviations are also greater, indicating that a few very high risk locations are driving these increases | ||||
| Wildfire Risk | ||||
| Scenario | Mean | St. Dev. | Min | Max |
| SPA | 108.2 | 31.2 | 31.6 | 203.8 |
| LU1 | 121.5 | 44.4 | 20.0 | 240.3 |
| LU2 | 118.1 | 42.6 | 16.0 | 234.4 |
| LU3 | 119.6 | 43.4 | 20.0 | 238.4 |
| LU4 | 118.4 | 42.1 | 23.3 | 234.6 |
| LU5 | 128.6 | 43.3 | 18.1 | 242.6 |
| LU6 | 158.7 | 36.1 | 16.9 | 248.5 |
| LU7 | 172.7 | 21.9 | 44.3 | 252.4 |
| LT1 | 108.3 | 42.7 | 15.0 | 228.6 |
| LT2 | 120.6 | 43.6 | 22.1 | 239.3 |
| LT3 | 120.5 | 43.3 | 20.0 | 238.4 |
| LT4 | 115.9 | 41.9 | 20.0 | 240.3 |
| LT5 | 115.7 | 42.7 | 20.0 | 239.8 |
| LT6 | 113.4 | 43.9 | 20.0 | 240.4 |
| LT7 | 83.9 | 27.7 | 20.0 | 192.4 |

|
| Figure 7. Wildfire risk maps from land-tenure scenarios. a) LT1, b) LT2, c) LT6 and d) LT7. Scenarios resulting in greater agricultural land use (a and b) produce different wildfire risk patterns than those with lesser agricultural land use (c and d). Risk values are relative for each map – darker colours indicate greater risk. The line of high-risk running roughly horizontally across all maps is due to a road running through the landscape. |

|
| Figure 8. Wildfire risk maps from land-use scenarios. a) Original SPA land use, b) LU1, c) LU2, d) LU5 and e) LU7. Maps for b) to d) have similar spatial patterns, reflecting the convergence of land-use scenarios to similar land-cover configurations (see Figure 6). Risk values are relative for each map – darker colours indicate greater risk. The line of high-risk running roughly horizontally across all maps is due to a road running through the landscape. |
BALMANN, A. (1997). Farm-based modelling of regional structural change: A cellular automata approach. European Review of Agricultural Economics 24(1): 85-108.
BOUSQUET, F. and C. Le Page (2004). Multi-agent simulations and ecosystem management: a review. Ecological Modelling 176(3-4): 313-332.
CHISHOLM, M. (1962). Rural Settlement and Land Use: An Essay in Location. London, Hutchison University Library.
CLIFF, A. D., P. Haggett and R. Martin (1997). Michael Chisholm: An appreciation. Regional Studies 31(3): 205-210.
DEADMAN, P., D. Robinson, E. Moran and E. Brondizio (2004). Colonist household decision making and land-use change in the Amazon Rainforest: an agent-based simulation. Environment and Planning B-Planning & Design 31(5): 693-709.
EVANS, T. P., A. Manire, F. de Castro, E. Brondizio and S. McCracken (2001). A dynamic model of household decision-making and parcel level landcover change in the eastern Amazon. Ecological Modelling 143(1-2): 95-113.
GROVE, A. T. and O. Rackham (2001). The nature of Mediterranean Europe: An ecological history. London, Yale University Press.
HAPPE, K., K. Kellerman and A. Balmann (2006). Agent-based analysis of agricultural policies: an illustration of the agricultural policy simulator AgriPoliS, its adaptation, and behavior. Ecology and Society 11(1): 49.
HARVEY, D. W. (1966). Theoretical Concepts and Analysis of Agricultural Land-Use Patterns in Geography. Annals of the Association of American Geographers 56(2): 361-374.
HLTD. (2002). Human Life-Table Database, Spain 1998-1999. Retrieved 25/07/2006, from http://www.lifetable.de/data/MPIDR/ESP_1998-1999.txt.
HUIGEN, M. G. A. (2004). First principles of the MameLuke multi-actor modelling framework for land use change, illustrated with a Philippine case study. Journal of Environmental Management 72(1-2): 5-21.
MANSON, S. M. (2005). Agent-based modeling and genetic programming for modeling land change in the Southern Yucatan Peninsular Region of Mexico. Agriculture, Ecosystems & Environment 111(1-4): 47-62.
MATHEVET, R., F. Bousquetb, C. Le Page and M. Antona (2003). Agent-based simulations of interactions between duck population, farming decisions and leasing of hunting rights in the Camargue (Southern France). Ecological Modelling 165(2-3): 107-126.
MATTHEWS, R. and P. Selman (2006). Landscape as a focus for integrating human and environmental processes. Journal of Agricultural Economics 57(2): 199-212.
MAZZOLENI, S., G. di Pasquale, M. Mulligan, P. di Martino and F. C. Rego, Eds. (2004). Recent dynamics of the Mediterranean vegetation and landscape. Chichester, UK, John Wiley & Sons.
MCGARIGAL, K., S. A. Cushman, M. C. Neel and E. Ene (2002). FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps. Amherst, Massachusetts.
MILLINGTON, J. D. A. (2005). Wildfire risk mapping: considering environmental change in space and time. Journal of Mediterranean Ecology 6(1): 33-42.
MILLINGTON, J. D. A. (2007). Modelling Land-Use/Cover Change and Wildfire Regimes in a Mediterranean Landscape. PhD Thesis, Department of Geography. London, King's College London.
MILLINGTON, J. D. A., G. L. W. Perry and R. Romero-Calcerrada (2007). Regression techniques for examining land use/cover change: A case study of a Mediterranean landscape. Ecosystems 10(4): 562-578.
MINISTERIO DE HACIENDA (2005). D.G. de Castro. Madrid, Spain.
MORAN, W. (1994). Rural Settlement and Land-Use - Chisholm,M. Progress in Human Geography 18(1): 60-62.
MORENO, J. M., A. Vazquez and R. Velez (1998). Recent history of forest fires in Spain. Large forest fires. J. M. Moreno. Leiden, Backhuys Publishers: 159-185.
MUNTON, R. J. C. (1994). Rural Settlement and Land-Use - Chisholm,M. Progress in Human Geography 18(1): 59-60.
PARKER, D. C., S. M. Manson, M. A. Janssen, M. J. Hoffmann and P. Deadman (2003). Multi-agent systems for the simulation of land-use and land- cover change: A review. Annals of the Association of American Geographers 93(2): 314-337.
PECO, B., F. Suarez, J. J. Onate, J. E. Malo and J. Aguirre (2000). Spain: first tentative steps towards an agri-environmental programme. Agri-environmental policy in the European Union. H. J. Buller, G. A. Wilson and A. Holl. Aldershot, UK, Ashgate: 145-168.
PERRY, G. L. W. and N. J. Enright (2002). Humans, fire and landscape pattern: understanding a maquis- forest complex, Mont Do, New Caledonia, using a spatial 'state- and-transition' model. Journal of Biogeography 29(9): 1143-1158.
PERRY, G. L. W. and J. D. A. Millington (2008). Spatial modelling of succession-disturbance dynamics in forest ecosystems: Concepts and examples. Perspectives in Plant Ecology, Evolution and Systematics 9(3-4): 191-210.
ROMERO-CALCERRADA, R. (2000). La valoración socioeconómica en la planificación de espacios singuales: Las Zonas de Especial Protección de Aves. PhD Thesis Thesis, Departamento de Geografia. Alcalá de Henares, Universidad de Alcalá.
ROMERO-CALCERRADA, R., C. Novillo, J.D.A. Millington and I. Gomez-Jimenez (2008). GIS analysis of spatial patterns of human-caused wildfire ignition risk in the SW of Madrid (Central Spain). Landscape Ecology 23(3): 341-354.
ROMERO-CALCERRADA, R. and G. L. W. Perry (2004). The role of land abandonment in landscape dynamics in the SPA 'Encinares del rio Alberche y Cofio' central Spain, 1984-1999. Landscape and Urban Planning 66(4): 217-232.
SAURA, S. and J. Martinez-Millan (2000). Landscape patterns simulation with a modified random clusters method. Landscape Ecology 15(7): 661-678.
VON Thünen, J. (1826). Die isolierte Staat in Beziehung auf Landwirtshaft und Nationalökonomie; English translation by Wartenberg CM in 1966. New York, Pergamon Press.
WAINWRIGHT, J. (2008). Can modelling enable us to understand the role of humans in landscape evolution? Geoforum 39(2): 659-674.
WAINWRIGHT, J. and J. B. Thornes (2004). Environmental issues in the Mediterranean: Processes and perspectives from the past and present. London, Routledge.
WILENSKY, U. (2005). NetLogo. http://ccl.northwestern.edu/netlogo/, Center for Connected Learning and Computer-Based Modeling. Northwestern University, Evanston, IL.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]