Ayse Mumcu and Ismail Saglam (2008)
Marriage Formation/Dissolution and Marital Distribution in a Two-Period Economic Model of Matching with Cooperative Bargaining
Journal of Artificial Societies and Social Simulation
vol. 11, no. 4 3
<https://www.jasss.org/11/4/3.html>
For information about citing this article, click here
Received: 13-Sep-2007 Accepted: 08-Jun-2008 Published: 31-Oct-2008
 Abstract
Abstract(1) Eij(t) = fij[ei(t)+ej(t)]
where the linear productivity parameters are nonegative real numbers and satisfy fij = fji.
(2) πi(j;Ωt)=max{biei(t),ui(j,t)+min{Eij(t),(1/2)[Eij(t)+di(j,Ωt)-dj(i,Ωt)]}}
where a nonnegative real number bi denotes the productivity parameter of the linear technology that converts agent i's endowment into end-of-period utility when he/she is single. Equation (2) ensures that all the surplus from a marriage is distributed and each agent gets when married at least as great as when he/she is single.
Thus, the period 2 endowment of man i who divorces from woman j at the end of period 1 is
(3) ei(2)= (1-a)[πi(j;Ω1) - ui(j,1)]- c
and the period 2 endowment of woman j who divorces from man i at the end of period 1 is[12]
(4) ej(2)=πj(i;Ω1) - uj(i,1) +a[πi(j;Ω1) - ui(j,1)]- c.
(5) ui(k,2)=ui(k,1)-ciu.
Agent i feels no emotional distress if he/she does not divorce from his/her mate.
(6) x(m,t)=πm(μ(m,t);Ωt) for all m є M, and x(w,t)=πw(μ(w,t);Ωt) for all w є W,
(7) there do not exist agents m є M and w є W such that πm(w;Ωt)>x(m,t) and πw(m;Ωt)>x(w,t).
Procedure CR(F,Ωt[F]):
Step 1: Pick any match p=(m,w) є F. We construct the reduced market Ω't[F] from Ωt[F] by setting the match p as unproductive, i.e.
(8) πm(w;Ω't[F])=bmem(t) and πw(m;Ω't[F])=bwew(t)
and letting Ω't[F]=Ωt[F] for all pairs in F\{p}.
Step 2: Using payoffs for p assumed in Step 1 and computed equilibrium payoffs CR(F\{p},Ωt[F\{p}]) for the marriages in F\{p}, compute the men-optimal stable matching and the implied payoff structure x'(.,t) for Ω't[F].[16]
Step 3: Set the disagreement payoffs of spouses in p to their payoffs calculated in Step 2, i.e.,
(9) dm(w;Ωt[F])=x'(m,t)-um(w,t) and dw(m;Ωt[F])=x'(w,t)-uw(m,t).
By conditions (8) and (9), the threat points of the pair (m,w) in the market Ωt[F] are taken as their equilibrium payoffs in the reduced market Ω't[F] (net of the emotional utilities from their current mates), where they are forced to remain single while all other agents can still exploit all of their opportunities.
Step 4: Compute equilibrium payoffs of p using the Marriage rule.
Marriage Rule: For the agents forming a given pair, calculate the bargaining payoffs using equation (2). Divorce the agents if and only if at least one of the agents is not worse off by remaining single. In that case, assign to both agents in the pair the payoffs from being single.
Step 5: Repeat steps 1-4 for each match p in F.
Step 6: Using payoffs for each p in F as calculated in Step 4, compute the men-optimal stable matching and the implied payoffs for each match in F.
| Table 1: Parameter values | |
| Tastes |
um1(w1,1), um1(w2,1), um2(w1,1), um2(w2,1) { 0.28, 0.59, 0.94, 1.31, 1.72, 2.15, 2.62} |
| uw1(m1,1), uw1(m2,1), uw2(m1,1), uw2(m2,1) {0.24, 0.50, 0.77, 1.09, 1.44, 1.86, 2.35} |
|
| cum1, cum2, cuw1, cuw2
{0.39, 0.49, 0.60, 0.70, 0.81, 0.9, 1.02} |
|
| Endowments | em1(1), em2(1), ew1(1), ew2(1) {1.04, 2.64, 4.80, 7.51, 10.78, 14.60, 18.98} |
| Productivity parameters | fm1w1, fm1w2, fm2w1, fm2w2 {0.50, 0.75, 1.00, 1.25, 1.50, 1.75, 2.00} |
| bm1, bm2, bw1, bw2 {0.44, 0.66, 0.87, 1.09, 1.30, 1.52, 1.73} |
|
| Policy variables | a, c {0.13, 0.25, 0.38, 0.50, 0.63, 0.75, 0.88} |
| Table 2: Frequency values of parameters in datasheet | |
| 343 |
um1(w1,1), uw2(m2,1), cum1, em1(1), fm1w1, bm1, c |
| 49 | um1(w2,1), uw1(m2,1), cum2, em2(1), fm1w2, bm2 |
| 7 | um2(w1,1), uw2(m1,1), cuw1, ew1(1), fm2w1, bw1 |
| 1 |
um2(w2,1), uw1(m1,1), cuw2, ew2(1), fm2w2, bw2, a |
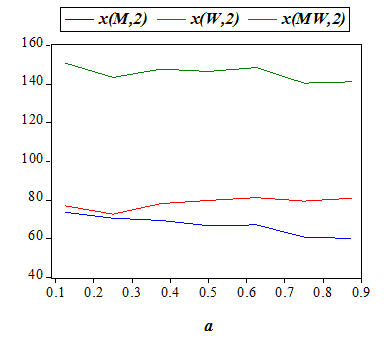
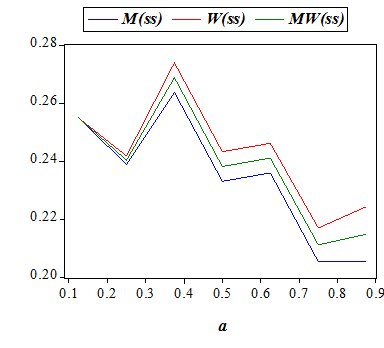
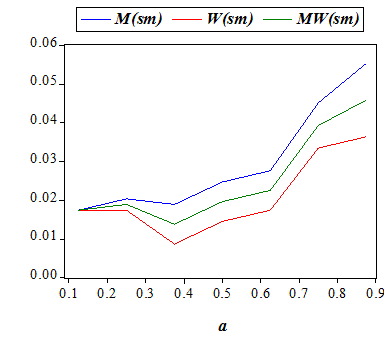
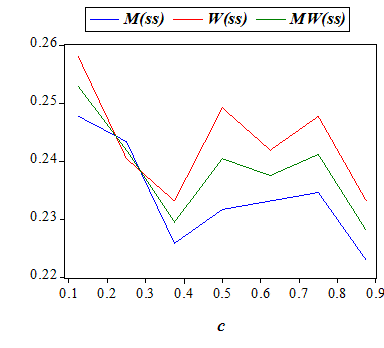
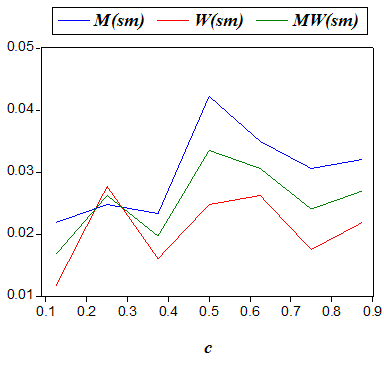
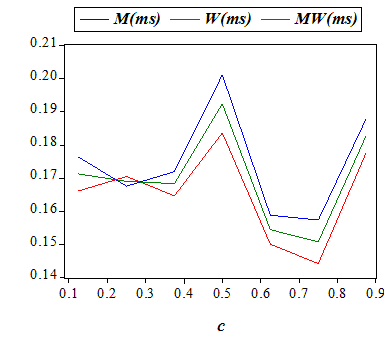
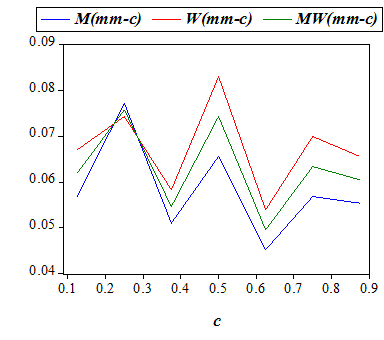
For the model parameters a and c we shall below analyze the variation in the average values (using 343 observations for each value of these two input variables) of the output variables in the list ( x(M,2), x(W,2), x(MW,2), M(ss), M(sm), M(ms), M(mm-c), M(mm-n), W(ss), W(sm), W(ms), W(mm-c), W(mm-n), MW(ss), MW(sm), MW(ms), MW(mm-c), MW(mm-n) ) . Here, x(M,2), x(W,2), and x(MW,2) are respectively the total payoffs of men, women, and the whole society, in the second period, while for any group Z in {M,W,MW} (men, women, society) the output variables Z(ss),Z(sm), Z(ms),Z(mm-c),Z(mm-n) respectively denote the frequencies of 'being single in both periods, married only in the second period, married only in the first period, married with distinct mates in the two periods, married with the same mate in both periods'. We should note that M(mm-n) and W(mm-n), and hence MW(mm-n), always take the same values.
| Table 3: Marital status (percentage distribution) | |||||
| Male |
M(ss) 23.41 |
M(sm) 3.00 |
M(ms) 17.45 |
M(mm-c) 5.83 |
M(mm-n) 50.31 |
| Female | W(ss) 24.32 |
W(sm) 2.08 |
W(ms) 16.53 |
W(mm-c) 6.75 |
W(mm-n) 50.31 |
| Society | MW(ss) 23.87 |
MW(sm) 2.54 |
MW(ms) 16.99 |
MW(mm-c) 6.29 |
MW(mm-n) 50.31 |
|
|
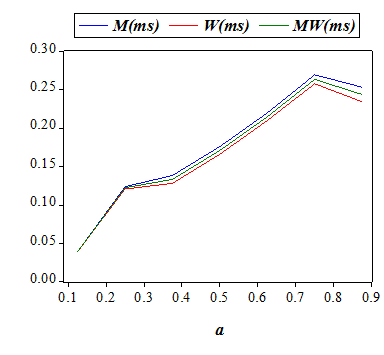
| Figure 1 | Figure 2 |
|
|
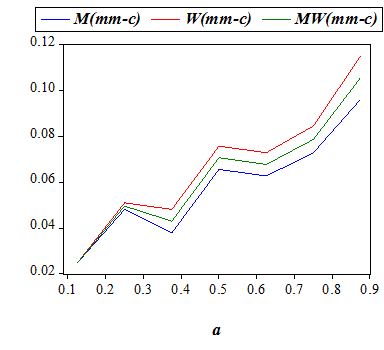
| Figure 3 | Figure 4 |
|
|
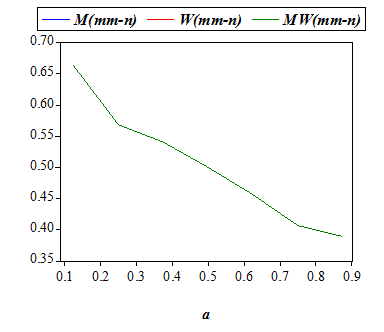
| Figure 5 | Figure 6 |
| Table 4: Summary of the effects of an increase in alimony rate (a) | |||||
| (+= increasing; - = decreasing; ~ = fluctuations) | |||||
| Men |
Women |
Society | |||
| Payoffs | - | + | - (slightly) | ||
| Frequencies | |||||
| Single-Single | - with ~ | - with ~ | - with ~ | ||
| Single-Married | + with ~ | + with ~ | + with ~ | ||
| Married-Single | + with ~ | + with ~ | + with ~ | ||
| Married-Married (Distinct Mates) | + with ~ | + with ~ | + with ~ | ||
| Married-Married (Same Mate) | - | - | - | ||
|
|
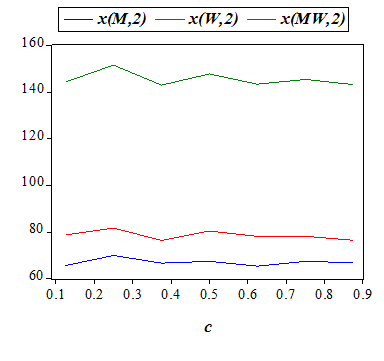
| Figure 7 | Figure 8 |
|
|
| Figure 9 | Figure 10 |
|
|
| Figure 11 | Figure 12 |
| Table 5: Summary of the effects of an increase in cost of divorce (a) | |||||
| (~ = fluctuations) | |||||
| Men |
Women |
Society | |||
| Payoffs | ~ (small) | ~ (small) | ~ (small) | ||
| Frequencies | |||||
| Single-Single | ~ (small) | ~ (small) | ~ (small) | ||
| Single-Married | ~ (small) | ~ (small) | ~ (small) | ||
| Married-Single | ~ (large) | ~ (large) | ~ (large) | ||
| Married-Married (Distinct Mates) | ~ (small) | ~ (small) | ~ (small) | ||
| Married-Married (Same Mate) | ~ (large) | ~ (large) | ~ (large) | ||
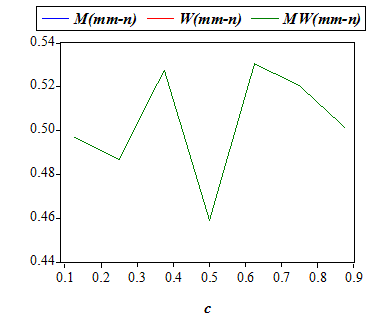
On the effect of divorce cost on the marital decisions, Becker (1976) argued that when divorce becomes easier, the number of people who are legally married may actually increase, which is only partially supported by our findings (Figures 9 and 11). However, empirical studies examining the impact of changing divorce legislation on marital status are also conflicting.[21] While Peters (1986, 1992) find no significant impact of changing divorce laws on divorce rates, Allen (1992) and Friedberg (1998) refute her finding. Recently, Wolfers (2006) reports that the divorce rate rose sharply following the adoption of unilateral divorce laws, but this rise was reversed within about a decade hence the long-run effects are ambiguous. Brien et al (2006) finds that decrease in divorce cost leads to a slight increase in the rate of marriage.
Step 1: Pick a permutation {pi,pj,pk,pl} of the pairs p1=(m1,w1), p2=(m1,w2), p3=(m2,w1), p4=(m2,w2).
Step 2: For the agents forming the pair pl, set the disagreement points equal to the payoffs from being single and calculate the bargaining payoffs using the Marriage Rule. Next, for the agents entering both pk and pl set the disagreement points to their calculated bargaining payoffs in the pair pl, and for the remaining agents in pk set the disagreement points to the payoffs from being single. Then, as the outcome of this step, determine the marital status and bargaining payoffs of the pair pk using the Marriage Rule.
Step 3: Repeat step 2 by interchanging the roles of pl and pk, and obtain the marital status and bargaining payoffs of the pair pl.
Step 4: Using the bargaining allocation obtained for pk and pl in steps 2 and 3, respectively, find the men-optimal stable matching for the agents in pk U pl.
Step 5: For the agents in pj, set the disagreement points to the bargaining payoffs obtained under the stable matching calculated in step 4 if these agents are also in pk or pl, and otherwise set them to the payoffs from being single. Then, find the marital status and payoffs for the pair pj using the Marriage Rule.
Step 6: Repeat steps 2-5 consecutively for the permutations (pi,pk,pj,pl) and (pi,pl,pj,pk), and obtain the marital status and payoffs of the pairs pk and pl, respectively.
Step 7: Let the pair pi be unproductive and the agents in pi have their payoffs from being single.
Step 8: Using the marital status and payoffs assumed or calculated for pi, pj, pk, and pl in steps 2-7, find the men-optimal stable matching and the implied payoffs.
Step 9: For the agents in pi, set the disagreement points to their bargaining payoffs calculated in step 8. Next, find the marital status and bargaining payoffs of the pair pi using the Marriage Rule.
Step
10: Repeat steps 2-9 consecutively for the
permutations (pj,pi,pk,pl), (pk,pi,pj,pl), (pl,pi,pj,pk),
and obtain the marital status and bargaining payoffs for the pairs pj, pk, and pl, respectively.
Step 11:
Using the marital status and bargaining payoffs
calculated for the pairs pi, pj,pk, and pl, determine the
men-optimal stable matching (hence the bargaining equilibrium) for the
marriage market.
The authors thank the editor and three anonymous reviewers of the JASSS for helpful suggestions and comments, and Gokhan Ozertan for helpful discussions. An earlier draft of this paper was written while the second author was affiliated with Bogazici University. The second author also acknowledges the support of the Turkish Academy of Sciences, in the framework of 'Distinguished Young Scientist Award Program' (TUBA-GEBIP). The usual disclaimer applies.
2McLanahan and Sandefur (1994) reports that, in 1995, the median income for female headed families with children was about one-third of the median income for married couple with children. Moreover, the rates to drop out of high school, to be idle, to experience teen births and not to take college education are higher for children living in single-parent households than for children from two-parent families. Page and Stevens (2002) finds that in the long-run (six or more years after the most recent divorce) family income falls by 40 to 45% after divorce, and food consumption is reduced by 17%.
3Of course, these assumptions make more sense in matching environments with a small population size.
4Each gender is restricted to have two representatives and live for two periods only to reduce the excessive number of calculations required to compute the recursive marriage equilibrium at each run of 2401 model simulations, which we will deal with in Section 3.
5 In the two-person cooperative bargaining literature, a bargaining problem consists of a convex and comprehensive set in the Cartesian plane of utilities and a particular point (disagreement point or threat point) in this set denoting the payoffs that the two agents will receive in case of disagreement. Bargaining solution is any procedure that computes the agreement point for each possible bargaining problem. In our model, we employ the Nash bargaining solution that maximizes the product of the individual utilities net of the disagreement payoffs (given exogenously or determined by outside options).
6We say that a matching is stable if no married individual prefers being single to his or her mate and if no pair of (unmatched) man and woman prefer each other to their mates, if any. A stable matching is called men-optimal if there exists no other stable matching which makes at least one man better-off (in terms of his mate) without making any other man in the society worse-off.
7Bargaining equilibrium of CR is criticized for having a drawback that an agent's utility obtained from his or her original marriage cannot affect his or her utility in an alternative marriage. As a remedy, Bennett (1988) proposes a new bargaining equilibrium, which always yields a core matching that is Pareto optimal and maximizes aggregate utility. However, this alternative solution rests upon much stronger behavioral assumptions about players, who must always be consistent in their conjectures and able to solve fixed point problems. While Bennett's bargaining equilibrium is uniquely appealing in the design and implementation of matching algorithms for a market designer who can rationally act on behalf of agents of any degree of rationality, the appropriate choice between the two equilibrium definitions by CR and Bennett in modelling the observed marital behavior in a particular society cannot be determined independently from the investigated rationality of the involved agents. In this paper, we prefer to use computationally more tractable equilibrium of CR for our simulations, consciously assuming away the full consistency of agents in the marriage market.
8According to McManus and DiPrete (2001), noncustodial parents are overwhelmingly male and alimony payments almost exclusively flow from men to women.
9Output (total utility) produced by a single-factor linear production technology is just a multiple or a fraction of the used factor (total endowments).
10The Nash solution (si,sj),
where si=(1/2)[Eij(t)+
di(j,Ωt)- dj(i,Ωt)] and
sj=(1/2)[Eij(t)+
dj(i,Ωt)- di(j,Ωt)], maximizes
the product [si-
di(j,Ωt)][sj- dj(i,Ωt)] subject
to si + sj=Eij(t).
11Here, we assumed for simplicity that the spouses share the divorce court expense of amount 2c and each spouse experiences emotional distress caused by divorce irrespective of who initiates divorce proceedings. These assumptions are less restrictive, of course, when the said cost parameters also represent material and psychological costs of moving to a new place to live.
12In equations 3 and 4 defining post-divorce wealth respectively for man i and woman j, emotional utilities are first subtracted from the payoffs in calculating alimonies to be received or paid since these utilities do not add to the total physical endowment that grows during the marriage of i and j in period 1.
13The stated common knowledge assumption, which is essential for the computability of the 'actual' bargaining equilibrium is definitely more demanding in marriage markets with a larger number of individuals. However, in situations where this informational assumption is not appealing, one can further assume that individuals will appeal to a Bayesian bargaining equilibrium which, of course, requires the use of commonly known priors on the defined structures of a marriage market.
14In fact, our two-period model also allows one to define and use a 'dynamic' equilibrium considering the life-time payoffs in individuals' decision problems. In such an equilibrium, a pair of poor agents that have extremely strong affections to each other may rather marry with rich and otherwise 'unattractive' individuals in the first period for the sole purpose of fortune-hunting (wealth-accumulating), and then they may divorce and marry with their 'genuine lovers' in the second period. In this paper, we assume away such far-sighted opportunistic motives, and use the single-shot equilibrium notion of CR in every period of our model.
15Gale and Shapley's (1962) DAA has been used to characterize group-optimal stable matchings in many market design problems, involving hospital-intern matching, college admissions and school choice.
16Using the bargaining payoff from an alternative mate as the threat point in marital bargaining, it is very convenient that for each potential partner, there is exactly one alternative match for each man and woman. This also works in an n-person generalization of the model since step 2 of the above procedure is recursively called until the set F shrinks to contain only two pairs.
17Using US data from the National Longitudinal Survey of Youth (NLSY79), Zagorsky (2005) finds that for respondents who married and stay married, per person net worth was 93 per cent higher than for single respondents.
18Coincidentally, the characteristics of our sample in terms of marital distribution fit quite well with the latest U.S. demographic data. According to U.S. Census Bureau, the marital status of people 15 years or over for all races as of March 2005 is reported as follows: 17.7% of the population is separated, divorced or widowed; 29% is never married, while 53.2% is married. The three figures are respectively 16.99%, 23.87% and 59.14% according to our simulations summarized in Table 3.
19Clearly, the above argument that a rise in the alimony rate increases the likelihood of remarrying after divorce has more support in bigger populations involving more than four individuals due to, on average, increased diversity in endowments and utilities.
20We have assumed that the couple productivity is, on the average, higher than the individual productivity. However, the produced output of each marriage (after being adjusted with respect to the outside options of the couples) is equally shared between the spouses. Thus, marrying may not be financially desirable for some wealthy individuals unless of course their prospective spouses are also sufficiently rich. We should also note that the intuition underlying why some individuals may choose to become single after divorce with big alimony payments is surely weaker in larger and more diverse societies where almost everyone faces financially attractive prospective mates at almost all wealth levels.
21The relaxation of divorce laws across many U.S. states during 1970s and 1980s reduced the legal cost of divorce substantially (see Brien et al 2006).
22Obviously, increases in the size and diversity of population in the marriage market strengthen the former argument while weakening the latter.
23For a
non-cooperative model of marriage, see Lundberg and Pollak (1994, 1996).
ALLEN D A (1992) ''Marriage and Divorce: Comment.'' American Economic Review, 82(3), pp. 679-685.
BECKER G S (1974) ''A Theory of Social Interactions.'' Journal of Political Economy, 82(6), pp. 1063-1094.
BECKER G S (1976) The Economic Approach to Human Behavior, Chigaco, IL: University of Chicago Press.
BECKER G S (1981, enlarged edition 1991) A Treatise on the Family, Cambridge, MA: Harvard University Press.
BENNETT E (1988) ''Consistent Bargaining Conjectures in Marriage and Matching.'' Journal of Economic Theory, 45(2), pp. 392-407.
BOUGHEAS S and GEORGELLIS Y (1999) ''The Effect of Divorce Costs on Marriage Formation and Dissolution.'' Journal of Population Economics, 12(3), pp. 489-498.
BRIEN M J, Liliard L A, and Steven S (2006) ''Cohabitation, Marriage, and Divorce in a Model of Match Quality.'' International Economic Review, 47(2), pp. 451-494.
CHIAPPORI P A and Weiss Y (2006) ''Divorce, Remarriage and Welfare: A General Equilibrium Approach.'' Journal of the European Economic Association, 4(2-3), pp. 415-426.
CRAWFORD V P and Rochford S C (1986) ''Bargaining and Competition in Matching Markets.'' International Economic Review, 27(2), pp. 329-348.
FRIEDBERG L (1998) ''Did Unilateral Divorce Raise Divorce Rates? Evidence from Panel Data.'' American Economic Review, 88(3), pp. 608-627.
GALE D and Shapley L S (1962) ''College Admissions and the Stability of Marriage.'' American Mathematical Monthly, 69(1), pp. 9-15.
GRAY J S (1998) ''Divorce-Law Changes, Household Bargaining, and Married Women's Labor Supply.'' American Economic Review, 88(3), pp. 628-642.
GREENWOOD J, Guner N, and Knowles J (2003) ''More on Marriage, Fertility, and the Distribution of Income.'' International Economic Review, 44(3), pp. 827-862.
LUNDBERG S and Pollak R A (1993) ''Separate Spheres Bargaining and the Marriage Market.'' Journal of Political Economy, 101(6), pp. 988-1010.
LUNDBERG S and Pollak R A (1994) ''Non-cooperative Bargaining Models of Marriage.'' American Economic Review Papers and Proceedings, 84(2), pp. 132-137.
LUNDBERG S and Pollak R A (1996) ''Bargaining and Distribution in Marriage.'' Journal of Economic Perspectives, 10(4), pp. 139-158.
MANSER M and Brown M (1980) ''Marriage and Household Decision Making: A Bargaining Analysis.'' International Economic Review, 21(1), pp. 31-44.
MCELROY M B and Horney M J (1981) ''Nash Bargained Household Decisions.'' International Economic Review, 22(2), pp. 333-349.
MCLANAHAN S and Sandefur G D (1994) Growing Up with a Single Parent: What Hurts, What Helps. Cambridge, MA: Harvard University Press.
MCMANUS P A and DiPrete T A (2001) ''Losers and Winners: The Financial Consequences of Separation and Divorce for Men.'' American Sociological Review, 66(2), pp. 246-268.
MILLER G F and Todd P M (1998) ''Mate Choice Turns Cognitive.'' Trends in Cognitive Sciences, 2(5), pp. 190-198.
NASH J F (1950) ''The Bargaining Problem.'' Econometrica, 18(2), pp. 155-162.
PAGE M E and Stevens A H (2002) ''Will You Miss Me When I Am Gone? The Economic Consequences of Absent Parents.'' NBER Working Paper Series, No: 8786.
PETERS H E (1986) ''Marriage and Divorce: Informational Constraints and Private Contracting.'' American Economic Review, 76(3), pp. 437-454.
PETERS H E (1992) ''Marriage and Divorce: Reply.'' American Economic Review, 82(3), pp. 686-693.
SAMUELSON P A (1956) ''Social Indifference Curves.'' Quarterly Journal of Economics, 70(1), pp. 1-22.
SANDEFUR G D (1996) ''Trends in AFDC Participation Rates: The Implications of Welfare Reform.'' Discussion Paper No: 1116-96, Madison: University of Wisconsin, Institute of Research on Poverty.
SIMAO J and Todd P M (2002) ''Modeling Mate Choice in Monogamous Mating Systems with Courtship.'' Adaptive Behavior, 10(2), pp. 113-136.
SIMAO J and Todd P M (2003) ''Emergent Patterns of Mate Choice in Human Populations.'' Artificial Life, 9(4), pp. 413-417.
STEVENSON B and Wolfers J (2007) ''Marriage and Divorce: Changes and their Driving Forces.'' Written for the Journal of Economic Perspectives, Symposium Celebrating 25 Years since Becker's Treatise on the Family.
TODD P M, Penke L, Fasolo B, and Lenton A P (2007) ''Different Cognitive Processes Underlie Human Mate Choices and Mate Preferences.'' Proceedings of National Academy of Sciences of the United States of America, 104(38), pp. 15011-15016.
WEISS Y and Willis R J (1997) ''Match Quality, New Information, and Marital Dissolution.'' Journal of Labor Economics, 15(1), Part 2: Essays in Honor of Yoram Ben-Porath, pp. S293-S329.
WOLFERS J (2006) ''Did Unilateral Divorce Raise Divorce Rates? A Reconciliation and New Results.'' American Economic Review, 96(5), pp. 1802-1820.
ZAGORSKY J L (2005) ''Marriage and Divorce's Impact on Wealth.'' Journal of Sociology, 41(4), pp. 406-424.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]