Shuguang Suo and Yu Chen (2008)
The Dynamics of Public Opinion in Complex Networks
Journal of Artificial Societies and Social Simulation
vol. 11, no. 4 2
<https://www.jasss.org/11/4/2.html>
For information about citing this article, click here
Received: 22-May-2006 Accepted: 10-Jul-2008 Published: 31-Oct-2008
 Abstract
AbstractGlobal or top-down control is often used when building a multi-agents model. What we mean by top-down control (Sanderson 2000) is not to manipulate the rules of individual behaviors, but instead use global information to govern. Alfred W. Hubler (2005) demonstrated the advantage of considering both patterns of information process — bottom-up and top-down, in comprehending the emerging patterns and dynamics. Although he demonstrated his theory through a model of the competition of plant seedlings for sunlight and water, it remains applicable and relevant to how society functions.
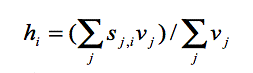
|
(1) |
where agent j connects with agent i. Figure 1 presents an example to show how to compute the environment influence.
|
|
| Figure 1. The process of calculating the environment influence |
|
|
(2) |
The indices β and 1-β are elasticity coefficients of environment influence and intrinsic factors, respectively.
|
|
| Figure 2. Comparison of two information updating mechanisms. Here, both simulations are run under the situation that the average connectivity is 30 and β is 0.5 with a regular graph. The left two graphs are lattices in which the color of each cell represents the opinion of one agent. The right two graphs are the evolving curves of public opinion. |
| Table 1: The average number of opinions in small world networks | ||||||
| SW Graph (p=0.3) | β | |||||
| AC | CPL | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| 6 | 7.46(1.30) | 3 | 3 | 3 | 3 | 3 |
| 10 | 4.27(0.22) | 3 | 3 | 3 | 3 | 3 |
| 30 | 2.60(0.04) | 3 | 3 | 2.96(0.20) | 2.04(0.81) | 1.71(0.62) |
| 50 | 2.20(0.05) | 3 | 3 | 2.23(0.43) | 1.46(0.51) | 1 |
| Table 2: The average number of opinions in random networks | ||||||
| Random Graph | β | |||||
| AC | CPL | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| 6 | 6.7(1.32) | 3 | 3 | 3 | 3 | 3 |
| 10 | 4.12(0.52) | 3 | 3 | 3 | 2.37(0.74) | 1.33(0.55) |
| 30 | 2.32(0.37) | 3 | 3 | 2.39(0.50) | 1 | 1 |
| 50 | 2.0(0.14) | 3 | 3 | 2.13(0.34) | 1 | 1 |
| Table 3: The average number of opinions in scale-free networks | ||||||
| Scale-free Graph | β | |||||
| AC | CPL | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| 5.99 | 3.85(0.28) | 3 | 3 | 3 | 3 | 1.63(0.97) |
| 9.99 | 3.11(0.17) | 3 | 3 | 3 | 1.25(0.53) | 1 |
| 29.97 | 2.30(0. 02) | 3 | 3 | 2.18(0.50) | 1 | 1 |
| 49.94 | 2.04(0.01) | 3 | 3 | 2.08(0.27) | 1 | 1 |
|
|
| Figure 3. Comparison of equilibrium between two connections with the same characteristic path length in a random network |
| Table 4: Minimum percentage of authorities for a controlled consensus | |||||
| AC | 10 | 20 | 30 | 40 | 50 |
| Nets | |||||
| Small world | 14% | 3% | 2.6% | 3.3% | 3.6% |
| Random | 6% | 2.6% | 2.4% | 2.7% | 3.1% |
| Scale-free | 6% (1%) | 6% (1%) | 6% (1%) | 6% (1%) | 6% (1%) |
Define a 2-D array, crunode[][], as the adjacent matrix of the network; Initialize crunode[][] by the regular network; For each vertex i For each vertex j connected with i Generate a random number, p, in [0, 1]; If p is smaller than the probability of rewiring, then Break the link between i and j; Select a vertex randomly and connect it with i; End_if End_for End_for
Initialize crunode[][] by the regular network; For each vertex i For each vertex j connected with i Broke the link between i and j; Select a vertex randomly and connect it with i; End_for End_for
Let d be the number of links that new vertexes are to be added in the net. Let k be the number of links that one vertex connects with others. Construct a regular net with 2*d vertexes. For the vertex i 2*d : size Do Select an existing vertex from 0 to i-1 randomly, marked by v; If v has not been linked with i, then Calculate the probability that i connects with v
If p(k) is larger than the generated random number in [0,1], then Connect i and v; Increase ki and kv by one. End_if End_if While ki is less than d End_for
For each agent i: Let utility[] store the utility of agents toward different choices; Let propensity[] store interior evaluation. Let influence[] store the influence from agents connecting with i; Let b be the psychological weight for balancing interior preference and outer influences. For each agent j connecting with i: For each decision modality k: If the decision of agent j is k, then increase the value of influence[k] by agent j's weight; End_for End_for For each decision modality k: utility[k] = (influence[])b (propensity[])1-b; End_for Update the state by comparing utility[k]. End_for
AMARO de Matos J (2004). Information Flow, Social Interactions and the Fluctuations of Prices in Financial Markets. Econometric Society 2004 Latin American Meetings
AMBLARD F and Deffuant G (2004). The Role of Network Topology on Extremism Propagation with the Relative Agreement Opinion Dynamics. Physica A: Statistical Mechanics and its Applications, 343:725-738
AXELROD R (1997). The Dissemination of Culture: A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution, 41( 2): 203-226
BARABÁSI A L and Albert R A (1999). Emergence of Scaling in Random Networks. Science, 286: 509-512
BARABÁSI A L, Albert R and Jeong H (1999). Mean-Field Theory for Scale-Free Random Networks. Physica A, 272: 173-187
BECHARA A (2004). The role of emotion in decision-making: Evidence from neurological patients with orbitofrontal damage. Brain and Cognition, 55: 30-40
BEN-NAIM E, Krapivsky P L and Redner S (2003). Bifurcations and Patterns in Compromise Processes. Physica D, 183: 190-204
BIKHCHANDANI S, Hirshleifer D and Welch I (1992). A Theory of Fads, Fashion, Custom, and Cultural Change as Informational Cascades. Journal of Political Economy, 100(5): 992-1026
BOSMAN R, Hennig-Schmidt H and Frans van Winden (2006). Exploring Group Decision Making in a Power-to-Take Experiment. Experimental Economics, 9: 35-51
CASE A C and Katz L F (1991). The Company You Keep: The Effects of Family and Neighborhood on Disadvantaged Youths. National Bureau of Economic Research Cambridge, Mass., USA
COBB C W and Douglas P H (1928). A Theory of Production. American Economic Review, 18(1):139-165
CONLEY T G, Topa G (2003). Identification of Local Interaction Models with Imperfect Location Data. Journal of Applied Econometrics, 18(5): 605-618
GALAM and Moscovici S (1991a). Towards a Theory of Collective Phenomena: Consensus and Attitude Changes in Groups. European Journal of Social Psychology, 21: 49-74
GALAM S and Moscovici S (1991b). Compromise versus Polarization in Group Decision Making. Defense Decision making, Russ. Psychol. J, 13: 93-103
GALAM S (2002). Minority opinion spreading in random geometry. Eur. Phys. J., B 25, 403-406
GALAM S (2003). Modelling rumors: the no plane Pentagon French hoax case. Physica A, 320: 571-580
GANDAL N (2002). Compatibility, Standardization, and Network Effects: Some Policy Implications. Oxford Review of Economic Policy, 18(1): 80-91
HOLLAND J H (1996). Hidden Order. Addison-Wesley Publishing Company
HOLLAND J H (1998). Emergence: From Chaos to Order. Oxford University Press
HUBLER A W (2005). Predicting Complex Systems with a Holistic Approach. Complexity, 10(3): 11-16
JAGER W (2000). Modelling Consumer Behaviour (dissertation), Veenendaal, the Netherlands: Universal Press
JONES J H and Handcock M S (2003). Sexual Contacts and Epidemic Thresholds. Nature, 423(5): 605-606
KAWAGUCHI D (2004). Peer effects on substance use among American teenagers. Journal of Population Economics, 17: 351-367
KATZ M L and Shapiro C (1994). Systems Competition and Network Effects. Journal of Economic Perspectives, 8(2): 93-115
KOOLE S L, Jager W, Van den Berg AE, Vlek C A J and Hofstee W K B (2001). On the Social Nature of Personality: The Influence of Self- and Peer-rated Extraversion and Agreeableness in a Social Dilemma. Personality and Social Psychology Bulletin
LAGUNA M F, Gusman S R, Abramson G, Goncalves S and Iglesias J R (2005). The Dynamics of Opinion in Hierarchical Organizations. Physica A, 351: 580-592
LEIBENSTEIN H (1950). Bandwagon, Snob, and Veblen Effects in the Theory of Consumers?Demand. Quarterly Journal of Economics, 64: 183-207
MAX-NEEF M (1992). Development and human needs. In: P. Ekins and M. Max-Neef (Eds.): Real-life economics: Understanding wealth creation. London, New York: Routledge
MCCLINTOCK C G (1978). Social values: Their definition, measurement and development. Journal of Research and Development in Education, 12: 121-137
MESSICK D M and McClintock C G (1968). Motivational basis of choice in experimental games. Journal of Experimental Social Psychology, 4: 1-25
MILLER J H and Page S E (2004). The Standing Ovation Problem. Complexity, 9(5): 8-16
MOSCOVICI S and Doise W (1992). Dissensions & consensus. Paris : PUF
POWEL N T (1951). Anatomy of Public Opinion. Prentice-Hall, New York
SATO Y, Akiyama E and Crutchfield J P (2004). Stability and Diversity in Collective Adaptation. Santa Fe Institute Working Paper, http://arxiv.org/abs/nlin.AO/0408039
SANDERSON I (2000). Evaluation in Complex Policy Systems. Evaluation, 6(4): 433-454
STAUFFER D (2001). The Sznajd model of consensus building with limited persuasion. http://arxiv.org/abs/cond-mat/0111419 v1
STAUFFER D (2002a). Better be third then second in a search for a majority opinion. http://arxiv.org/abs/cond-mat/0202357 v1
STAUFFER D (2002b). Frustration from Simultaneous Updating in Sznajd Consensus Model. http://arxiv.org/abs/cond-mat/0207598 v1
STAUFFER D and Meyer-Ortmanns H (2003). Simulation of Consensus Model of Deffuant et al on a Barab´asi-Albert Network. http://arxiv.org/abs/cond-mat/0308231 v2
SZNAJD-WERON K and Sznajd J (2000). Opinion evolution in closed community. Int. J. Mod. Phys. C, 11(6)
TASSIER T (2004). A Model of Fads, Fashions, and Group Formation. Complexity, 9(5): 51-61
VAZQUEZ A, Dobrin R, Sergi D, Eckmann J P, Oltvai Z N and Barabási A L (2004). The Topological Relationship between the Large-scale Attributes and Local Interaction Patterns of Complex Networks. Proceedings of the National Academy of Sciences, 101(52): 17940-17945
VAZQUEZ F, Krapivsky P L and Redner S (2003). Constrained opinion dynamics: freezing and slow evolution. J. Phys. A, 36, L61
VLEK C A J (1995). Technical versus socio-behavioral solutions to environmental problems: psychology's unexploited potential. Extended version of an invited lecture for the Environmental Psychology Division of the American Psychological Association, presented in New York
WATTS D J and Strogatz S H (1998). Collective Dynamics of Small-world Networks. Nature, 393: 440-442
WATTS D J, Dodds P S and Newman M E J (2002). Identity and Search in Social Networks. Science, 296(17): 1302-1305
WEISBUCH G, Deffuant G and Amblard F (2005). persuasion dynamics. Physica A, 353: 555-575
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]