Mikola Lysenko and Roshan M. D'Souza (2008)
A Framework for Megascale Agent Based Model Simulations on Graphics Processing Units
Journal of Artificial Societies and Social Simulation
vol. 11, no. 4 10
<https://www.jasss.org/11/4/10.html>
For information about citing this article, click here
Received: 23-Jun-2008 Accepted: 24-Sep-2008 Published: 31-Oct-2008
 Abstract
Abstract
|
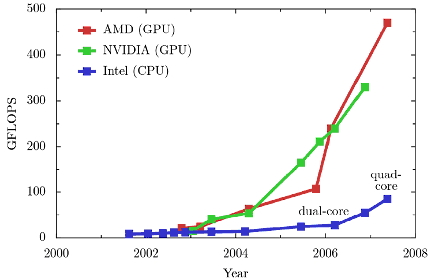
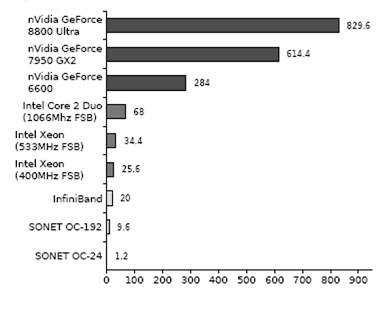
| Figure 1. GPU Performance Specs. (a) Computing Power Comparison. (b) Memory Bandwidth Comparison. (Silberstien 2007 ,D'Souza et al. 2007) |

|
| Figure 2. Various Environmental Parameters, Such as Obstacles or Scalar Fields, Are Stored in the Components of the Color Channels |
|
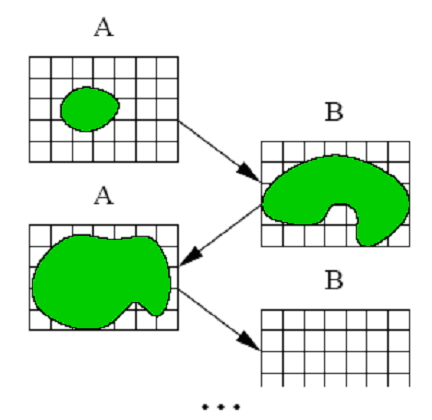
| Figure 3. The Ping-Pong Technique Forms the Basis for GPGPU Processing. Images are Iteratively Updated as They Rendered From one Frame Buffer to the Next |
|
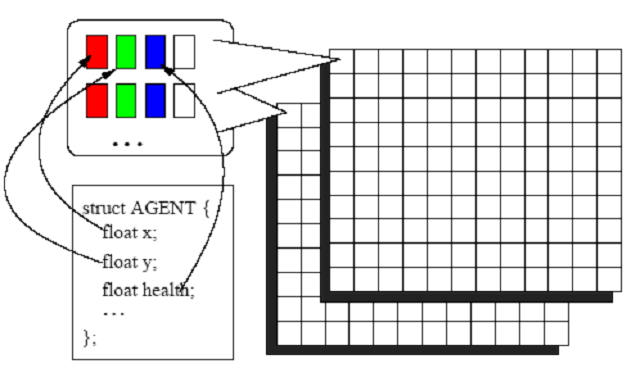
| Figure 4. An Encoding of the Agent State Into the Agent State Texture |
|
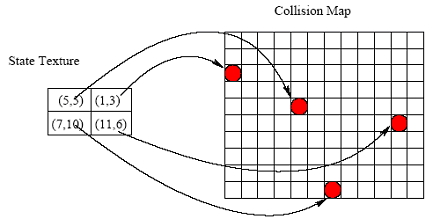
| Figure 5. Scattering the Agents |
|
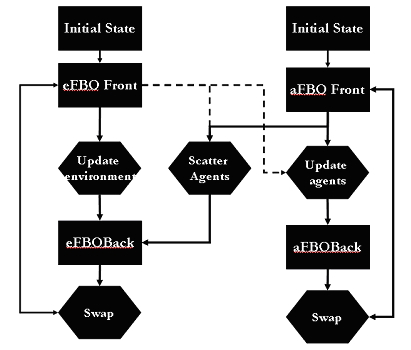
| Figure 6. Connecting Mobile Agents to Environment Through Scatter |

|
|
|
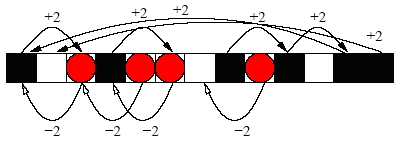
| Figure 7. A Simplified View of the Agent State Texture. Black Cells are Empty (Dead), and White Cells are Filled (Alive). Cells with a Circle are About to Replicate (Gravid) |

|
where r is a random integer in the range[1, n). The arithmetic in expression ai+r is evaluated modulo n, so for example a n+3 maps to a3. Moreover, it is trivial to evaluate both f and its inverse, f-1. Using equation 1, it is now possible to construct the following parallel agent allocation algorithm.

|

|
|
| Figure 8. Connecting Gravid Cells to Empty Cells |
|
|
| Figure 9. The Result of one Iteration of the Stochastic Allocation Algorithm |
|
|

|
|
|

|
|
| Figure 10. Performance Benchmarks vs Existing ABM Toolkits. The Environment was Set to 128x128. The Agent Population Was 500 |

|
| Figure 11. Screen Shot of The Simulation. There are 2 Million+ Agents on a 2560x1024 Environment Grid |
|
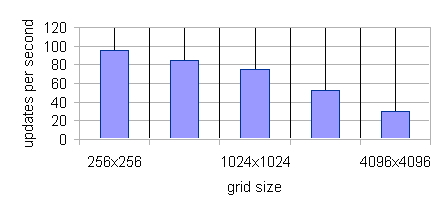
| Figure 12. Sugarscape Implementation Scaling with Environment Grid Size. There are 2 Million+ Agents in This Benchmark |
|
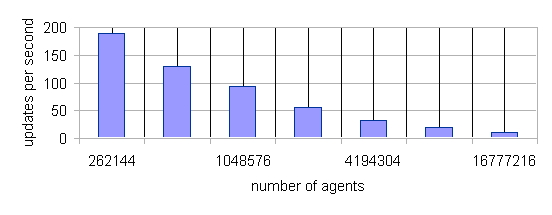
| Figure 13. Sugarscape Implementation Scaling with Agent Population. The Grid Size for This Benchmark is 2560x1024 |
|
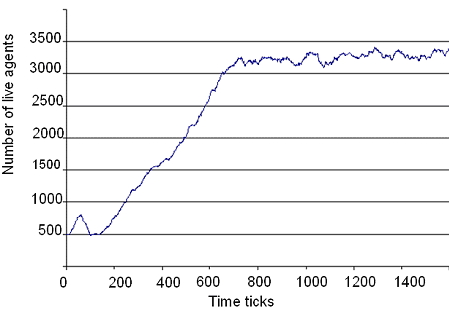
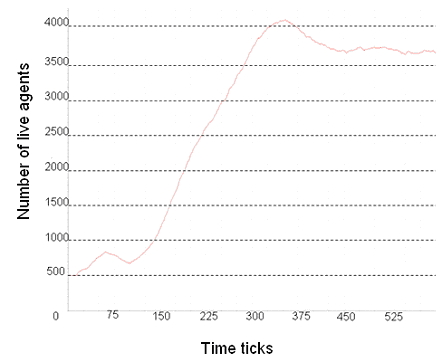
| Figure 14. Live Agent Population over Time (a) Output From the GPU implementation, (b) Output From MASON Implementation |
|
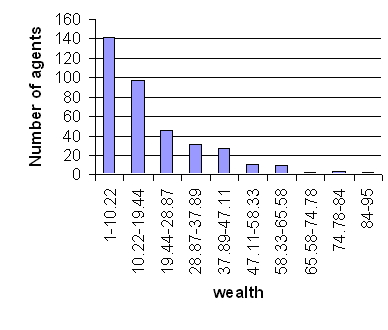
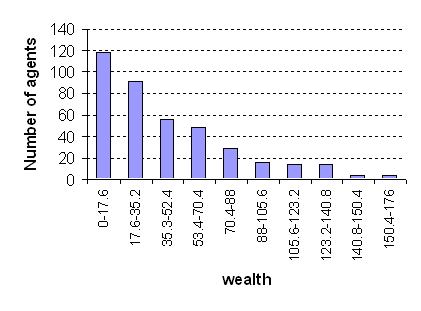
| Figure 15. Histograms of Wealth Distribution (a) Output From the GPU implementation, (b) Output From REPAST Implementation |
|
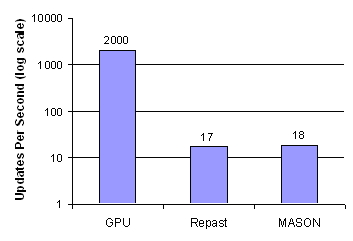
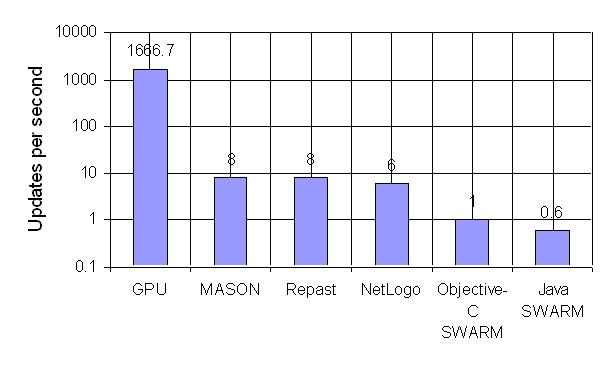
| Figure 16. Performance Benchmarks Against Existing ABM Toolkits. The Updates per Second for the GPU is About 1666.7 Frames per Second. MASON, the Fastest Toolkit Runs the Same Model at About 8 Frames per Second |
|
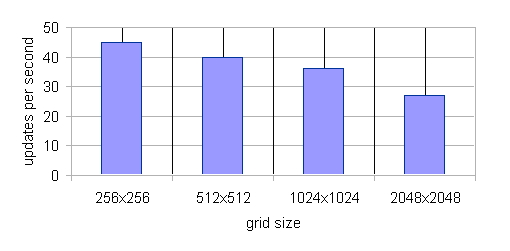
| Figure 17. Scaling of the StupidModel with Environment Grid Size. There are 2 Million+ Agent in this Benchmark |

|
| Figure 18. Screenshot of StupidModel Implementation. This Run has 1Million+ Agents on a 2560x1024 Environment Grid |
|
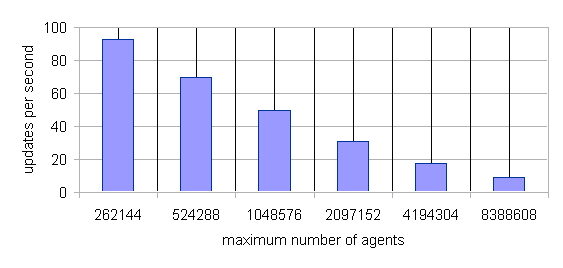
| Figure 19. Scaling of the StupidModel Implement with Agent Population Size. This Simulation Runs on a 2560x1024 Environment Grid |
BERNASCHI M, Castiglione F (2005) Computational Features of Agent-Based Models. International Journal of Computational Methods, 2(1).
BIGBEE A, Cioffi-Revilla C, Luke S (2007) Replication of Sugarscape Using MASON, Springer Series on Agent Based Social Systems, Springer Japan, 3, pp. 183-190. BONEBEAU E (1997) From Classical Models of Morphogenesis to Agent-Based Models of Pattern Formation. Artificial Life, 3 (3), pp. 191-211.
BONEBEAU E (2002) Agent-Based Modeling: Methods and Techniques to Simulate Human Systems. PNAS, 99(3), pp. 7280-7287.
BURKHART R (1994) The Swarm Multi-Agent Simulation System. OOPSLA '94 Workshop on "The Object Engine".
CALLIER F M, Desoer C A (2002) Linear System Theory. Springer-Verlag.
D'SOUZA R M, Lysenko M, Rahmani K (2007) Sugarscape on Steroids: Simulating Over a Million Agents at Interactive Rates. Proceedings of the Agent 2007 Conference, Chicago, IL.
DA-HUN T, Tang F, Lee T, Sarda D, Krishnan A, Goryachev A (2004) Parallel Computing Platform for Agent-Based Modeling of Multicellular Biological Systems. LNCS, 3320, pp.5-8.
ENGEL K, Hadwiger M, Kniss J M Lefohn A E, Salama C R, Weiskopf D (2004) Realtime Volume Graphics, In SIGGRAPH '04: ACM SIGGRAPH 2004 Course Notes, ACM Press, New York, NY, USA, 2004, p. 29.
EPSTEIN J M, Axtell R L (1996) Growing Artificial Societies: Social Science from the Bottom Up, MIT Press.
FIALKA O, Cadík M (2006) FFT and Convolution Performance in Image Filtering on GPU. In Proceedings of the conference on Information Visualization, IEEE Computer Society, Washington, DC, USA, 2006, pp. 609-614.
GODEKKE G (2005) Gpgpu Tutorials - Basic Math. Webpage at http://www.mathematik.uni-dortmund.de/ goeddeke/gpgpu/tutorial.html
HARRIS M J, Coombe G, Scheuermann T, Lastra A (2002) Physically-Based Visual Simulation on Graphics Hardware, In HWWS '02: Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, pp. 109-118.
HARRIS M J, Baxter W V, Scheuermann T, Lastra A (2003) Simulation of Cloud Dynamics on Graphics Hardware. In HWWS '03: Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, pp. 92-101.
HARRIS M (2006) Mapping computational Concepts to GPUs, GPU Gems 2, Addison-Wesley Publishers, pp. 493-508.
KAPASI U J, Rixner S, Dally W J, Khailany B, Ahn J H, Matson P, Owens J( 2003) Programmable Stream Processors. IEEE Computer, pp. 54-62.
KEYES R W (2005) Physical Limits of Silicon Transistors and Circuits. Rep. Prog. Phys., 68, pp. 2701-2746.
KHALIL H K (2002) Nonlinear Systems. Prentice Hall.
KOLB A, Latta L, Rezk-Salaman C (2004) Hardware-Based Simulation and Collision Detection for Large Particle Systems. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics Hardware, ACM Press, New York, NY, USA, pp. 123-131.
KRUGER J, Westermann R (2003) Acceleration Techniques for GPU-Based Volume Rendering. In Proceedings of the 14th IEEE Visualization 2003, IEEE Computer Society, Washington, DC, USA, 2003, p. 38.
LASSAO F, Hoppe H (2004)F. Losasso, H. Hoppe, Geometry Clipmaps: Terrain Rendering Using Nested Regular Grids. In SIGGRAPH '04: ACM SIGGRAPH 2004 Papers, ACM Press, New York, NY, USA, pp. 769-776.
LEES M, Logan M, Oguara T, Theodoropoulos G (2003) Simulating Agent-Based Systems with HLA: The Case of SIM AGENT Part-II. Proceedings of the 2003 European Simulation Interoperability Workshop, Stockholm, Sweden.
LOGAN B, Theodoropoulos G (2001) The Distributed Simulation of Multi-Agent Systems. Proceedings of the IEEE, 89(2), pp.174-186.
LUKE S, Cioffi-Revilla C, Sullivan K, Balan G (2005) MASON: A Multiagent Simulation Environment. Simulation, 81(7), pp. 517-527.
MASSAIOLI F,Castiglione F, Bernaschi M (2005) OpenMP Parallelization of Agent-Based Models. OpenMP, 31(10), pp.1068-1081.
MILLAN R, Rudomín I (2006) Impostors and Pseudo-Instancing for GPU Crowd Rendering, In Proceedings of the 4th International Conference on Compute Graphics and Interactive Techniques in Australasia and Southeast Asia, ACM Press, New York, NY, USA, 2006, pp. 49-55.
MORELAND K, Angel E (2003) The FFT on a GPU. In Proceedings of the ACMSIGGRAPH/EUROGRAPHICS conference on Graphics hardware, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, pp. 112-119.
NORTH M J, Collier N T, Vos J R (2006) Experiences in Creating Three Implementations of the Repast Agent Modeling Toolkit. ACM Transactions on Modeling and Computer Simulations, 16(1), pp. 1-25.
OWENS J D, Luebke D, Govindaraju N, Harris M, Krüger J, Lefohn A E, Purcell T (2005) A Survey of General-Purpose Computation on Graphics Hardware. In: Eurographics, State of the Art Reports, pp. 21-51.
PURCELL T (2004) Ray Tracing on a Stream Processor. Ph.D. Dissertation, Stanford University.
QUINN M J, Metoyer R, Hunter-Zaworski K (2003), Parallel Implementation of the Social Forces Model. Proceedings of the Second International Conference in Pedestrian and Evacuation Dynamics, pp. 63-74.
RAILSBACK S F, Lytinen S L and Grimm V (2005) StupidModel and Extensions: A Template and Teaching Tool for Agent-based Modeling Platforms. Webpage at http://condor.depaul.edu/~slytinen/abm/StupidModelFormulation.pdf
RESNICK M (1994) Turtles, Termites, and Traffic Jams: Explorations in Massively Parallel Microworld. MIT Press, Cambridge, MA, Webpage at http://education.mit.edu/starlogo/
SCHEUTZ M, Schermerhorn P (2006) Adaptive Algorithms for Dynamic Distribution and Parallel Execution of Agent-Based Models. Journal of Parallel and Distributed Computing, 66(8), pp.1037-1051.
SILBERSTIEN M (2007) High Performance Computing on GPUs Using CUDA, GPGPU Tutorial at SIGGRAPH07.
SINGLER J (2004) Implementation of Cellular Automata Using a Graphics Processing Unit. In proceedings of ACM Workshop on General Purpose Computing on Graphics Processors, Los Angeles, CA.
SOM T K, Sargent R G (2000), Model Structure and Load Balancing in Optimistic Parallel Discrete Event Simulation. Proceedings of the Fourteenth Workshop on Parallel and Distributed Simulation, pp. 147-154.
STAGE A R, Crookston N L, and Monserud R A (1993) An Aggregation Algorithm for Increasing the Efficiency of Population Models. Ecological Modelling, 68(3-4), pp. 257-271.
STRZODKA R, Doggett M, Kolb A (2005) Scientific Computing on Programmable Graphics Hardware. Simulation Modelling Practice and Theory, 13(8), pp. 667-681
SUSSMAN M, Crutchfield W, Papakipos M (2006) Pseudorandom Number Generation on the GPU. In Proceedings of ACM EUROGRAPHICS/SIGGRAPH Conference on Graphics Hardware.
WENDELL S, Dibble C (2007) Dynamic Agent Compression, JASSS, 10 (2) 9 https://www.jasss.org/10/2/9.html
WILENSKY U(1999) Netlogo. http://ccl.northwestern.edu/netlogo/
WOLFRAM S (2002), A New Kind of Science. Wolfram Media Inc., Champaign, IIlinois, US, United States.
ZEIGLER B P, Praehofer H, Kim T G(2000). Theory of modeling and simulation: Integrating discrete event and continuous complex dynamic systems. Second edition. Academic Press
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]