Modelling Socio-Technical Transition Patterns and Pathways
Journal of Artificial Societies and Social Simulation
vol. 11, no. 3 7
<https://www.jasss.org/11/3/7.html>
For information about citing this article, click here
Received: 06-Jan-2008 Accepted: 13-May-2008 Published: 30-Jun-2008
 Abstract
Abstract
|
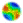
| Figure 1. The four phases of a transition. The y-axis is an appropriate indicator of the system's change, and the x-axis is time. From Rotmans et al. (2001) |
|
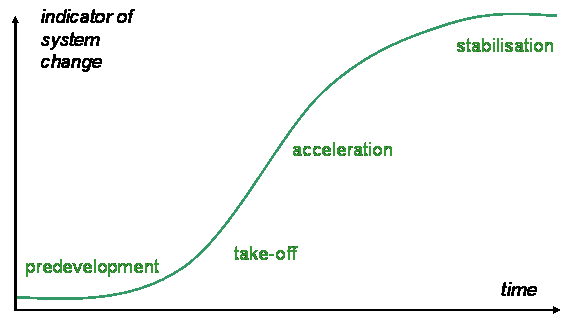
| Figure 2. Our 'transition laboratory' in which the model is run, with various options at run time (click image for a larger version) |
%20practices%20space.gif)
|
%20practices%20space.gif)
|
| Figure 3. Two illustrations of a two-dimensional practices space, with practice axes PX and PY. Left: regime and niches, which can move in the space and interact with each other. Right: the support canvas, showing supporters scattered in the practices space, coloured by the agent they support, red = regime (R), green = niche 1 (N1), blue = niche 2 (N2). | |
| pi,j = c(1-Di,j) | (1) |
where c is the clustering parameter, set to 0.2 by default. When two niches cluster, the resulting agent (niche or ENA if its strength is above the T1 threshold) has the sum of their structure parameters PC and IC, and the average of their locations in the practices space.
| pr,n= c(1-1.2Dr,n) | (2) |
using the same c as the clustering parameter, set to 0.2 by default. The reduction of the probability of absorption at greater distances and the maximum distance at which a niche can be absorbed both express the regime's limited ability to change. Similarly to clustering, the resulting (regime) agent after absorption has the sum of the structure parameters and the average of the locations of the original agents. While the first makes a small difference to the regime, the second allows it to take a big step in the direction it was heading in the practices space, and is much faster than adaptation.
| CDLCt= m.CDLCt-1+(1-m)DCt | (3) |
where DC is the distance to the nearest agent, and m represents the supporter's 'memory' of previous (dis)satisfaction. For each supporter, the normalised CDLC determines the probability of a niche emerging at the supporter's location. For supporter i the probability of a niche emerging at each timestep is:
| pi = b.CDLCi /CDLCmean | (4) |
where b is the birth parameter, set to 0.01 by default.
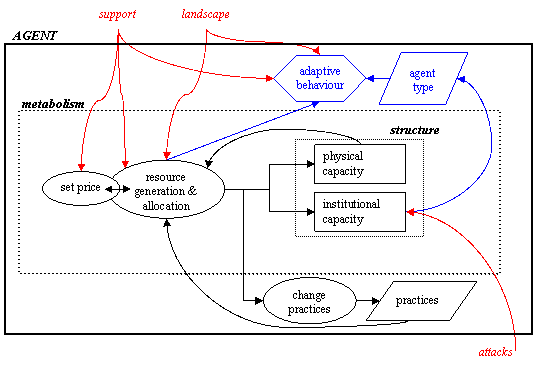
|
| Figure 4. Agent metabolism as part of the agent. Resource gathering depends on external support and landscape, and internally on price, physical capacity and practices. Resources are spent on physical and institutional capacity, as well as on adaptation through changing practices. Institutional capacity in turn determines the type of the agent (niche, ENA, or regime); it can be reduced through external attacks. |
| R = price . output | (5) |
where R is resources. We define output as:
| output = min(PC + 0.5, support.CONSTsupport) | (6) |
where PC is physical capacity. The constant is calibrated to match a 'healthy' regime with support = 0.8 and physical capacity PC = 100, so CONSTsupport = 125. The full resource equation includes miscellaneous effects of landscape and policy as well:
| R = price . output . f(landscape,policy) | (7) |
Physical and Institutional capacity are calculated by depreciation d and an addition from resources:
| PCt = PCt-1(1-d)+CONSTPC.R.fPC | (8) |
| ICt = ICt-1(1-d)+CONSTIC.R.fIC | (9) |
where fPC and fIC are the allocation fraction of resources to PC and IC, respectively.
| attractivenessi,j = α.sj -Di,j2 | (10) |
where s is the agent's normalised strength, D is the normalised distance between the supporter and the agent, and α is the relative weight of the agent's strength, set between 0 and 1. A value of α = 1 would indicate that the strength of the agent was a major factor, whereas a value of α = 0 would indicate that satisfaction with the agent was the only consideration. The default value is α = 0.05. We replace the distance with an ongoing measure of the supporter's satisfaction with the agent over time. We measure the cumulative dissatisfaction level (CDL) as the previous dissatisfaction level combined with normalised distance:
| CDLt = m . CDLt-1 + (1-m)Dt | (11) |
where m represents the supporter's 'memory' of previous (dis)satisfaction. The default value for m is 0.5. The attractiveness function over time is therefore:
| attractivenessi,j = α.sj -CDLi,j2 | (12) |
Finally, we consider 'miscellaneous' effects which change supporters' views and choices, which could include prices, or socio-political considerations which are not captured in the practices space. This gives us:
| attractivenessi,j = α.sj -CDLi,j2 +Impi.Effj | (13) |
where Eff is the effect value for agent j, and Imp is the importance of the effect for supporter i.
| Table 1: Model timestep summary: the actions, in order, at each timestep of the model | ||
| Action | Sub-actions | Notes |
| Landscape | . update signals/policy events | update the landscape signals, from which the pressure field is calculated |
| Metabolism | . set IC . set PC . set output . set price . set resources | for each agent, calculate the metabolism parameters from support and other parameter values |
| Normalise | . set normalised strength | set strength of each agent to normalised IC |
| Supporters | . move . set distances . set CDLs . choose agent to support | . calculate probability/direction of move from pressure field . calculate distances from agents' locations . calculate CDL from distances and previous CDL |
| Agents' Movement | . decide strategy . move | . set strategy by agent type . move by strategy |
| Mechanisms | . birth . absorption . clustering . transform 1 . transform 2 | activate all that are appropriate |
| Table 2: Model setup for the transformation pathway | ||
| Example 1: cesspools to sewer systems, The Netherlands, 1850-1900 | ||
| Agents | Regime | local government, departments of public works |
| Niche 1 | hygienist doctors / hygiene movement frontiers: limited to high hygiene and public responsibility (i.e., high values on practices 1 and 2) | |
| Practices | Axis 1 | efficiency/hygiene of waste disposal practices |
| Axis 2 | role of authorities in public life (individual v public responsibility for health) | |
| Frontiers | Niche 1 | limited to high values in practice 1 (i.e., a niche of hygienist doctors or a hygiene movement necessarily demands high hygiene standards) |
| Mechanisms | Adaptation | regime expected to adapt its practices considerably |
| Absorption | regime expected to absorb the hygiene niche | |
| Landscape signals | 1 | urbanisation following industrialisation (more pressure on the hygiene systems) effect: slow supporter movement up practice 1, 1865-1890 |
| 2 | norms of hygiene increase effect: increasing supporter movement up practice 1, slow supporter movement up practice 2, 1850-1890 | |
| 3 | democratisation and more public responsibility effect: strong supporter movement on practice 2, slight movement on practice 1, 1880-1890 | |
| Table 3: Model setup for the de-alignment / realignment pathway | ||
| Example 2: horses to carriages, USA 1870-1920 | ||
| Agents | Regime | Horse drawn carriages and trams |
| Niche 1 | electric trams | |
| Niche 2 | bicycles | |
| Niche 3 | electric cars | |
| Niche 4 | petrol cars | |
| Niche 5 | steam engine cars | |
| Practices | Axis 1 | personal mobility v public mobility |
| Axis 2 | length of commuting / day-to-day trips | |
| Frontiers | All | All agents are limited in their movement from their original positions, as the practices refer largely to the nature of the technology and infrastructure of each mode of transport. |
| Mechanisms | Clustering | used in some runs — different car niches expected to cluster |
| Landscape signals | 1 | hygiene movement (problems with horses) effect: lowers attractiveness of regime, reaching maximum at 1890 |
| 2 | (sub)urbanisation effect: increases average length of commute and day-to-day trips, i.e., movement up practice 2, 1870-1895. | |
| 3 | increase in personal mobility (following success of cars and bicycles) effect: supporter movement down practice 1, 1885-1910 | |
| 4 | technological innovation — electricity: reduced price of trams 1880-1900 | |
| 5 | technological innovation — mass production: reduced car prices 1890-1910 | |
| attractivenessi,j = α.sj - CDLi,j2 +ImphygieneEffhygiene,j + Impprice(1-pricej) | (14) |
It was assumed for simplicity that the importance of the effects was the same for all supporters, and the values were set at Imphygiene= 0.15 and Impprice = 0.05. Effhygiene rises linearly from 0 in 1870 to a maximum of 1 in 1890 for horse-based transport, and is 0 for all other agents. Price was set to 1 by default for all agents. In some runs, the price for electric trams was set at 2 at the beginning of the simulation and the price of all cars at 5; the prices then dropped either linearly or suddenly to 1 (dynamic learning curves were not included). The success of the transition here would be in regime change. It will be judged to be a de-alignment / realignment pathway if support disperses among various agents when the original regime collapses, and two or more niches compete for supremacy after the collapse, rather than one regime quickly replacing another.
| Table 4: Model setup for the technological substitution pathway | ||
| Example 3: sailing ships to steamships, Britain 1850-1900 | ||
| Agents | Regime | Sailing ships |
| Niche 1 | Steam ships | |
| Practices | Axis 1 | speed & reliability |
| Axis 2 | price | |
| Frontiers | Regime | Sailing ships have limited room for improvement of speed and reliability, as is represented by a frontier of this practice. |
| Mechanisms | Adaptation | adaptation of the steamship niche — becoming more reliable and eventually cheaper — play a major role in this pathway. |
| Transformation | The steam ship niche is expected to transform from niche to ENA, then to regime. The incumbent regime of sailing ships expected to transform down to ENA, and perhaps niche. | |
| Landscape signals | 1 | emigration = increased passengers effect: increased demand for fast, reliable transport, i.e., supporters move up practice 1 |
| 2 | Suez Canal opening effect: step function in 1869 which increases steam ships' speed and reduces their price. | |
| 3 | increased business expectations for cheap, fast transport effect: moves supporters up practice 1, and a little bit down practice 2 | |
| Table 5: Model setup for the reconfiguration pathway | ||
| Example 4: traditional factories to mass production, USA 1850-1900 | ||
| Agents | Regime | (starts as) traditional factories |
| Niches | none at start; birth of niches as new innovations appear. | |
| Practices | Axis 1 | organisation of production (including power source — water / steam / electricity; individual craftsmen / craft workshops / production lines) |
| Axis 2 | mechanisation and division of labour | |
| Mechanisms | Birth | various improvements expressed as the emergence of new niches. |
| Absorption | the regime expected to absorb niches as it assimilates new ideas and changes its practices | |
| Landscape signals | 1 | Electricity as pervasive technology (enables more mechanisation and electricity as power source) effect: moves supporters a lot up practice 1 and a little up practice 2 |
| 2 | The Efficiency Movement (increasing production lines and division of labour) effect: moves supporters a lot up practice 2 and a little up practice 1 | |
| 3 | The rise of professional engineers and industrial managers and accountants (increasing organisation and division of labour) effect: moves supporters up practice 1 and practice 2 | |
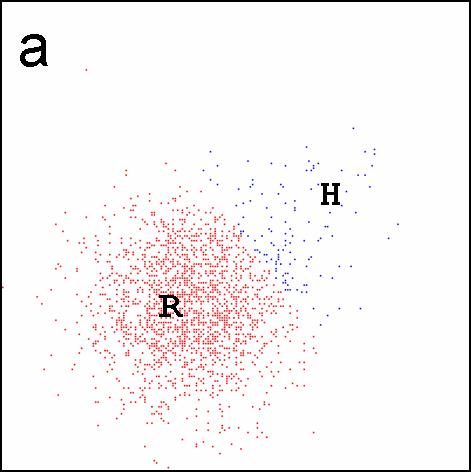
|
||
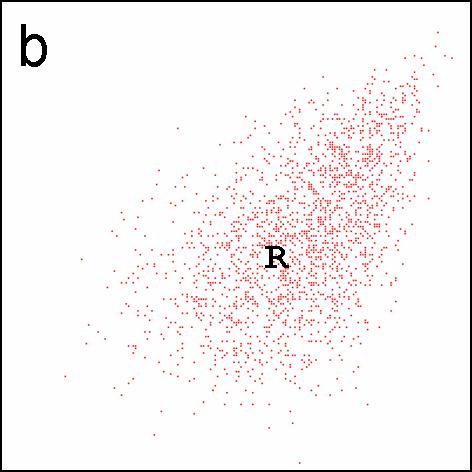
|
||
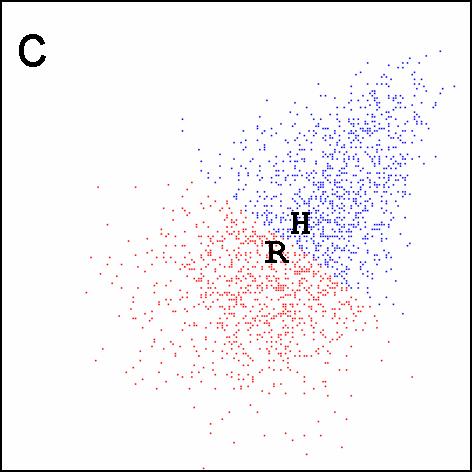
|
||
| Figure 5. Supporters and agents in the practices space in example 1: the x- and y-axes are practices 1 and 2, respectively; supporters are located at their ideal practices, and marked as dots, coloured red if they support the original regime and blue if they support the hygiene movement; R marks the position of the original regime agent, H that of the hygiene movement agent. The three panels show the beginning of a run (a), the end of a run with absorption (b) and the end of a run without absorption (c). | ||
|
|
|
|
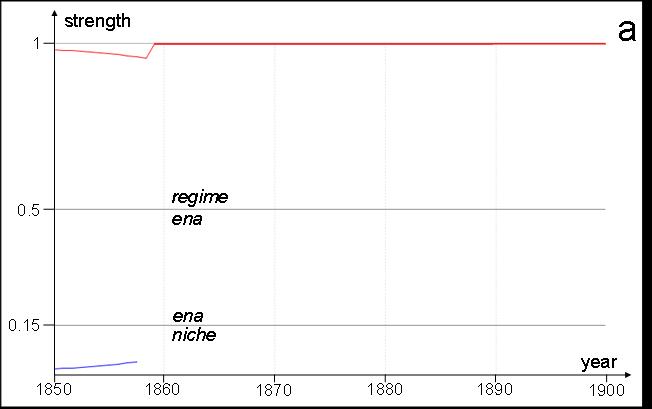
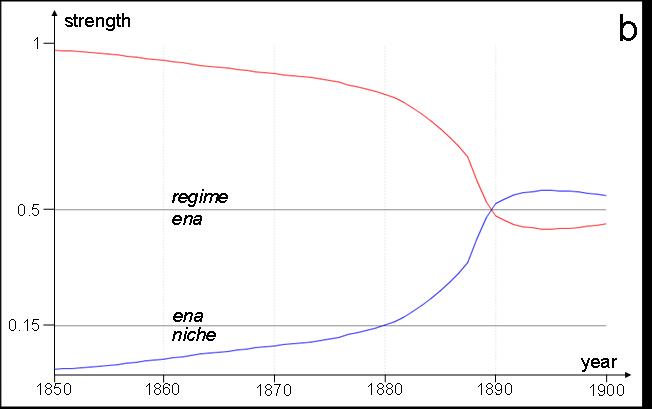
| Figure 6. Normalised agent strengths in example 1: a run with absorption (a) and one without (b). The x-axis is time (years), the y-axis normalised strength, with vertical sections differentiating niches (bottom), ENAs (middle) and regime (top). The red line is the original regime agent, the blue is the hygiene movement agent. | |
|
|
|
|
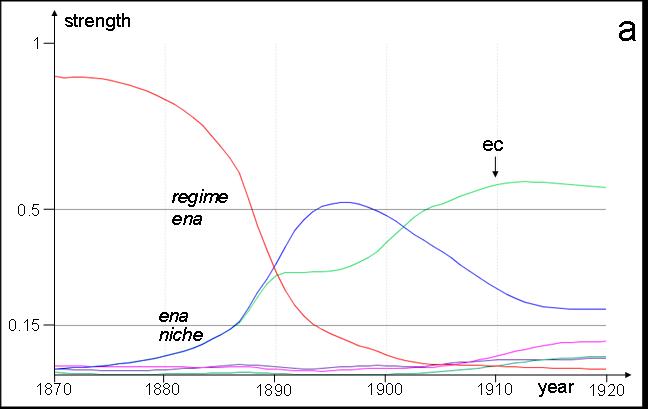
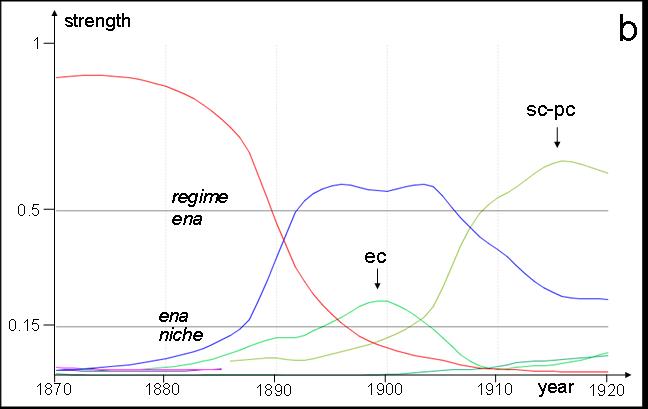
| Figure 7. Normalised agent strengths in example 2: without price effects (a) and with sudden price changes (b). The x-axis is time (years), the y-axis strength, with vertical sections differentiating niches (bottom), ENAs (middle) and regime (top). The red is horse-based transport, blue = electric trams, light green (ec) = electric cars, pink = petrol cars, olive green (sc-pc, in b only) = cluster of steam and petrol cars. | |
|
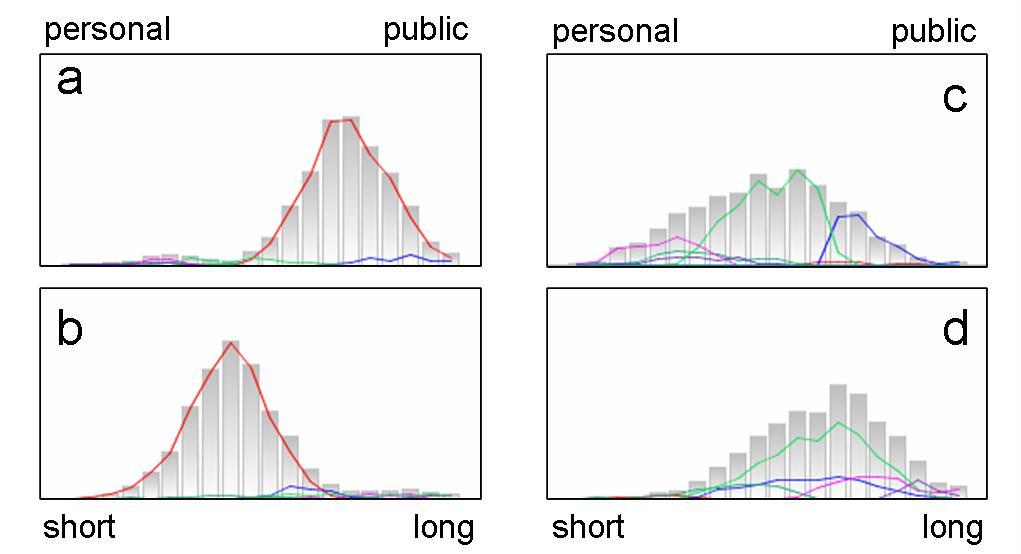
| Figure 8. Supporter preference distribution in a typical run of example 2: the x-axis shows (discrete) ideal points for the practice, bars show number of supporters with that ideal point. Coloured lines show strength of support for different agents by ideal practices. Distribution is shown at the beginning (a, b) and end (c, d) of a run, for personal/public mobility preference (a, c), and average length of day-to-day trips (b, d). At the beginning of the run supporters tend to favour public mobility over personal, and have fairly short day-today trips, with almost all choosing horse-based transport (red). At the end of a run there is more personal mobility and longer trips, with most supporters favouring electric cars (green), but some preferring trams (blue), petrol cars (pink) or other modes of transport. |
|
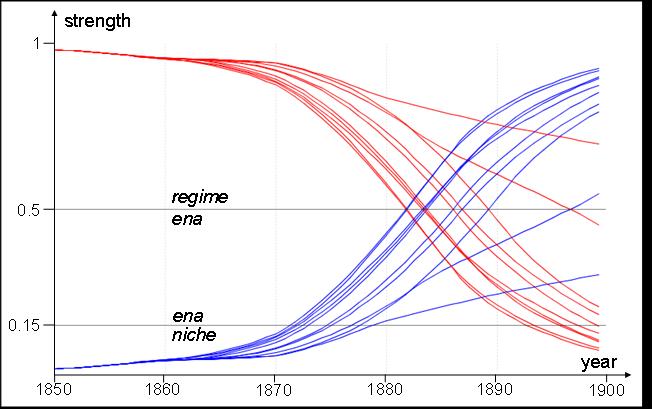
| Figure 9. Normalised agent strengths for ten runs in example 3: The x-axis is time (years), the y-axis strength, with vertical sections differentiating niches (bottom), ENAs (middle) and regime (top); the red lines are the sailing ship agent, the blue lines the steam ship agent. This batch of ten runs shows steam ships becoming the new regime in nine runs, with steamships gaining strength and support more slowly in the last one. Note: there is symmetry in each run, due to there being only two agents. |
|
|
|
|
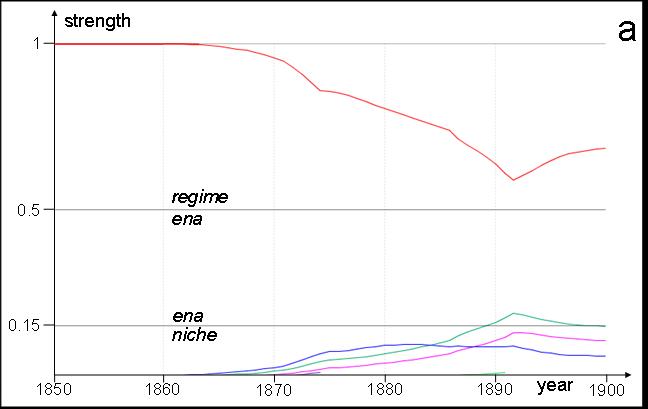
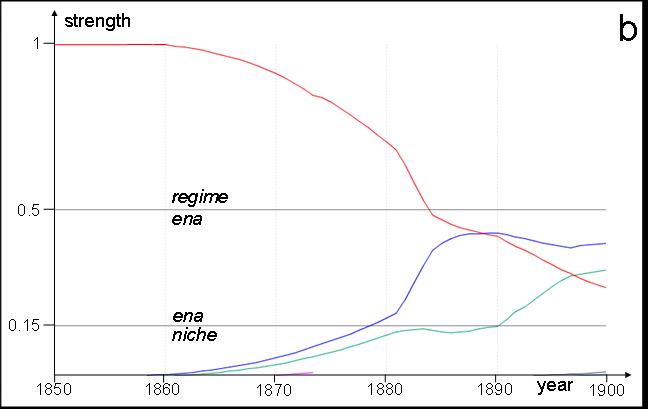
| Figure 10. Normalised agent strengths in example 4: the red line is the regime, all others are randomly generated niches. The x-axis is time (years), the y-axis strength, with vertical sections differentiating niches (bottom), ENAs (middle) and regime (top). In run (a) the regime absorbs two niches and fights competition from three others. In run (b) the regime absorbs only one niche, and later collapses, leaving no regime at the end of the run. | |
| Ai(t+1) = (1 - delta) Ai(t) + delta Si(t) / Stotal(t) | (15) |
where A is attractiveness of agent i to the investor, S is the strength (as shares of registered tonnage of Great Britain in year t), and delta the fraction of resources to be reallocated.
|
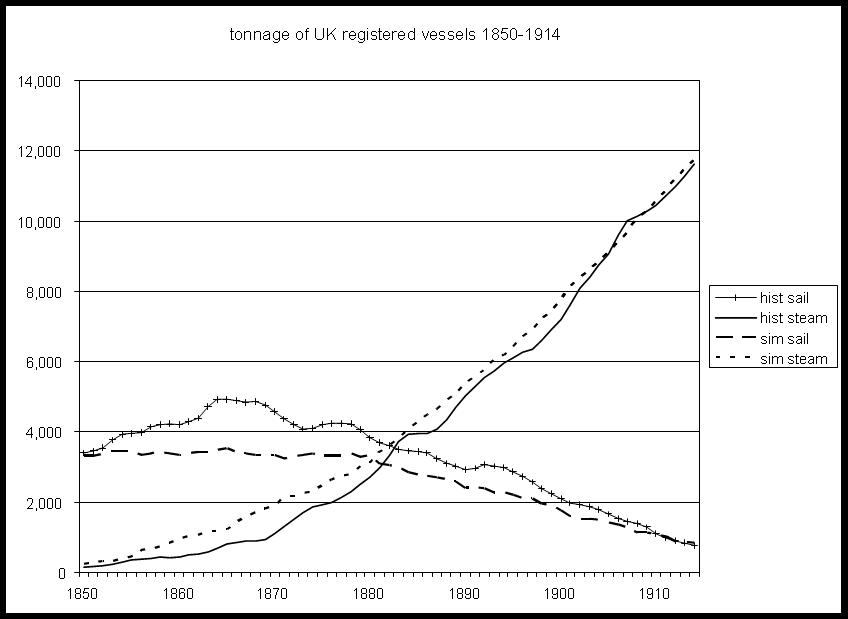
| Figure 11. Comparison of registered tonnage of sail and steam from historical data with model simulation results (Köhler and Schilperoord unpublished) |
2 While this description is for regime change, we can expect a similar period of rapid change followed by stabilisation if a regime is transformed.
3 The transformation mechanism, in which an agent switches from one type to another, is not to be confused with the transformation transition pathway.
BERGMAN, N, Whitmarsh, L and Köhler, J (2008). Transition to sustainable development in the UK housing sector: from case study to model implementation. UEA: Tyndall Centre Working Paper.
DIEDEREN, P, van Meijl, H, Wolters, A, and Bijak, K (2003) 'Innovation Adoption in Agriculture: Innovators, Early Adopters and Laggards'. Cahiers d'Economie et Sociologie Rurales, 67, pp. 30-50.
DOSI G (1984) Technical Change and Industrial Transformation, London: Macmillan.
ELZEN, B, Geels, F W and Green, K (Eds.) (2004) System Innovation and the Transition to Sustainability: Theory, Evidence and Policy, Cheltenham, UK: Edward Elgar.
GEELS F W (2002) Understanding the dynamics of technological transitions: a co-evolutionary and socio-technical analysis, Enschede, The Netherlands: Twente University Press.
GEELS F W (2005a) 'Processes and patterns in transitions and system innovations: Refining the co-evolutionary multi-level perspective'. Technological Forecasting and Social Change, 72(6), pp. 681-696.
GEELS F W (2005b) Technological Transitions and System Innovation: A Coevolutionary and Socio-Technical Analysis, Cheltenham, UK: Edward Elgar.
GEELS, F W (2006a) 'The hygienic transition from cesspools to sewer systems (1840-1930): The dynamics of regime transformation'. Research Policy, 35(7), pp. 1069-1082.
GEELS, F W (2006b) 'Major system change through stepwise reconfiguration: A multi-level analysis of the transformation of American factory production (1850-1930)'. Technology in Society, 28(4), pp. 445-476.
GEELS F W and Schot J (2005) 'Taxonomy of transitions pathways in socio-technical systems' Presented at workshop by the ESRC Sustainable Technologies Program, May 12, 2005, London.
GEELS F W and Schot J (2007) 'Typology of sociotechnical transition pathways.' Research Policy, 36, pp. 399-417.
GIDDENS A (1984) The Constitution of Society, Cambridge: Polity Press.
HAXELTINE, A, Whitmarsh, L, Bergman N, Rotmans, J, Schilperoord, M and Köhler, J (2008) A Conceptual Framework for transition modelling. International Journal of Innovation and Sustainable Development 3(1-2), pp. 93-114.
HOOGMA R, Kemp, R, Schot, J and Truffer, B (2002) Experimenting for Sustainable Transport Experimenting for Sustainable Transport: the approach of strategic niche management, Routledge: London, New York.
KEMP, R and Rip, A (1998) "Technological Change". In Rayner, S and Malone, E L (Eds.), Human Choice and Climate Change, Volume 2 (pp. 327-399), Columbus, Ohio: Battelle Press.
KÖHLER, J, Grubb, M, Popp, D and Edenhofer, O (2006) 'The transition to endogenous technical change in climate-economy models: A technical overview to the Innovation Modeling Comparison Project'. Energy Journal, pp. 17-55.
KÖHLER, J, Whitmarsh, L, Nykvist, B, Schilperoord, M, Bergman, N and Haxeltine, A (forthcoming). Mobility ISA Case Study Report. Submitted to Technological Forecasting & Social Change.
KÖHLER, J and Schilperoord, M (unpublished). Report on a historical calibration case study for the MATISSE WP9 transitions model: A new perspective on the transition from Sail to Steam in Ocean Shipping. MATISSE Final Deliverable Report.
LAVER M (2005) 'Policy and the dynamics of political competition'. American Political Science Review, 99(2), pp. 263-281.
LOORBACH D and Rotmans J (2006) "Managing transitions for sustainable development". In Olshoorn X and Wieczorek A J (Eds.) Understanding Industrial Transformation: views from different disciplines Dordrecht: Springer.
NOBLE T (2000) Social Theory and Social Change, Basingstoke: Macmillan.
ROGERS, E M (1995) Diffusion of Innovations (4th ed.). New York: Simon and Schuster.
ROTMANS, J, Kemp, R and van Asselt, M (2001) 'More evolution than revolution: transition management in public foreign policy'. Foresight 3(1), pp. 15-31.
ROTMANS J (2005). Societal innovation: Between dream and reality lies complexity, Rotterdam: Inaugural Address, Erasmus Research Institute of Management.
SCHWOON M (2005). Simulating The Adoption of Fuel Cell Vehicles. Working Paper, FNU-59 Research unit Sustainability and Global Change, Hamburg University.
SMITH, A, Stirling, A and Berkhout, F (2005) 'The governance of sustainable socio-technical transitions'. Research Policy, 34(10), pp. 1491-1510.
TURNPENNY, J, Weaver, P M, Rotmans, J, Haxeltine, A and Jordan, A (2007) 'Methods and Tools for Integrated Sustainability Assessment'. Chapter 9 in George C and Kirkpatrick C (Eds.) Impact Assessment for a New Europe and Beyond, Cheltenham, UK: Edward Elgar.
WEAVER P M (2005) 'Integrated Sustainability Assessment: toward a new paradigm'. In Blaas W (Ed.) Der Öffentliche Sektor — Forschungsmemoranden: Multi-level Governance for Sustainability. 31(1-2), pp. 47-53.
WHITMARSH L and Nykvist B (2008). Integrated sustainability assessment of mobility transitions: Simulating stakeholders' visions of and pathways to sustainable land-based mobility. International Journal of Innovation and Sustainable Development. 3(1-2), pp. 115-127.
WHITMARSH L and Wietschel M. (2008). Sustainable transport visions: What role for hydrogen and fuel cell vehicle technologies? Energy and Environment 19(2), pp. 207-226.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]