Ravi Bhavnani, Dan Miodownik and Jonas Nart (2008)
REsCape: an Agent-Based Framework for Modeling Resources, Ethnicity, and Conflict
Journal of Artificial Societies and Social Simulation
vol. 11, no. 2 7
<https://www.jasss.org/11/2/7.html>
For information about citing this article, click here
Received: 07-Nov-2007 Accepted: 18-Feb-2008 Published: 31-Mar-2008
 Abstract
Abstract
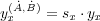
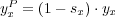
where sx ∈ [0,1] denotes the share of revenue going to the controlling agent.
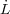 in control of a given cell (note that support need not be limited to leaders of one's own group, and that accountability is limited to leaders alone). This measure ranges from -10 to +10 (where -10 denotes total support for leader Ḃ, +10 denotes total support for leader Ȧ, and 0 denotes neutrality) and depends upon: (i) current revenue; (ii) changes in revenue over time; (iii) the coercive power of the "accountable agent"; and (iv) the ethnicity of the "accountable agent". Specifically, we take the difference between actual revenue yP and a reference revenue yref P and the difference between yP and the past revenue ypastP. Let ypastP be weighted sum of past revenue:
in control of a given cell (note that support need not be limited to leaders of one's own group, and that accountability is limited to leaders alone). This measure ranges from -10 to +10 (where -10 denotes total support for leader Ḃ, +10 denotes total support for leader Ȧ, and 0 denotes neutrality) and depends upon: (i) current revenue; (ii) changes in revenue over time; (iii) the coercive power of the "accountable agent"; and (iv) the ethnicity of the "accountable agent". Specifically, we take the difference between actual revenue yP and a reference revenue yref P and the difference between yP and the past revenue ypastP. Let ypastP be weighted sum of past revenue:
ypastP(t + 1) = kws ypastP(t) + (1 - kws) yP(t)
where kws ∈ [0,1] represents the "length" of memory. It follows that as kws decreases, the rate at which a peasant "forgets" the past increases. We then specify a function h(ca) which describes how peasant support is affected by the coercive power ca of the leader in control of a cell, such that h(ca) begins at -1 for no coercive power, rises linearly to +1 for ca = cideal, falls linearly to -1 for ca = coppressive, and remains at -1 for ca ≥ coppressive. This function is then weighted by a parameter kCP. Lastly, support is affected by ethnic salience, such that if ei>0 then ke equals -1 if the peasants and leader are from different groups, 1 if the peasants and leader are from the same group, and 0 if ei < 0.11 Adding these terms, and inserting them into a logistic function 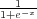 yields:
yields:
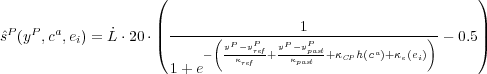
where 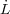 equals -1 for Ḃ, +1 for Ȧ, and 0 otherwise. The update rule for sP(t) is:
equals -1 for Ḃ, +1 for Ȧ, and 0 otherwise. The update rule for sP(t) is:
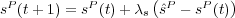
where λs captures the "inertia" or the rate at which a peasant adapts her sympathy to changes in economic well being.
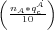 over mobility radius m
over mobility radius m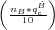 over mobility radius m
over mobility radius m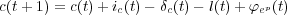
 P), the coercive power (cȦ and cḂ) of leaders in the cell, and the cell's distance from the capital city, with -10 denoting complete control by Ḃ of a cell and +10 denoting complete control by Ȧ of a cell.
P), the coercive power (cȦ and cḂ) of leaders in the cell, and the cell's distance from the capital city, with -10 denoting complete control by Ḃ of a cell and +10 denoting complete control by Ȧ of a cell.
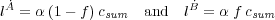
where f ∈ [0,1] is the conflict outcome variable (f = 1 being total victory by Ȧ and f = 0 total victory by Ḃ), csum = cȦ + cḂ is the sum of all coercive powers involved in the fight, and α is a parameter that determines the intensity of conflict (by scaling the losses). We define the conflict outcome variable f using the log-ratio of coercive power log 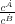 , measuring control in cells surrounding the conflict qsur =
, measuring control in cells surrounding the conflict qsur = 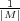 ∑ i
∑ i M qci (where M denotes the conflict cell and its Moore Neighbors, qci denotes control in cell i), using a distance function
M qci (where M denotes the conflict cell and its Moore Neighbors, qci denotes control in cell i), using a distance function 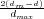 , and introducing a stochastic term X ~ N(0,σ2) where σ2 is the amount of randomness we seek to introduce. Taking the sum of these terms in the logistic function
, and introducing a stochastic term X ~ N(0,σ2) where σ2 is the amount of randomness we seek to introduce. Taking the sum of these terms in the logistic function 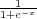 yields:
yields:
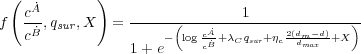
where λc weights the influence of control in surrounding cells, and where ηc weights the influence of the geography. Control of the cell under contention shifts to the victorious agent, and in the case of widespread conflict, may result in a change of the EGIP.
|
|
|
|
|
Table 1. Range of Experiments with REsCape

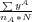 , where r denotes the range over which per capita income is calculated, what we refer to as the "per-capita range", which can vary from 0 (only the current cell in which the peasant is located) to 10 (the entire landscape), permitting peasants to make "local" or myopic calculations, or by contrast, calculations based on "global" information. By a similar logic, per capita income for group B is given by ypcB,r =
, where r denotes the range over which per capita income is calculated, what we refer to as the "per-capita range", which can vary from 0 (only the current cell in which the peasant is located) to 10 (the entire landscape), permitting peasants to make "local" or myopic calculations, or by contrast, calculations based on "global" information. By a similar logic, per capita income for group B is given by ypcB,r = 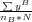 . Ethnicity becomes salient when a peasant's per capita income is smaller than the per-capita income of nominal rivals. It follows that for a member of group A, ethnic salience is give by eiA =
. Ethnicity becomes salient when a peasant's per capita income is smaller than the per-capita income of nominal rivals. It follows that for a member of group A, ethnic salience is give by eiA = 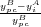 , and by the same logic, the salience of ethnicity B would given by eiB =
, and by the same logic, the salience of ethnicity B would given by eiB = 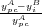 .
.
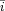 :
: 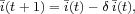
with sector-specific depreciation rates δki, δai,δaa and δag ≤ 1. Every investment i0 decays exponentially assuming continuous time and no further investment:
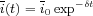
Note that investment in industrial production is constrained by an upper limit 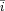 max, such that
max, such that 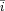 ki,max= μki,max *k and
ki,max= μki,max *k and 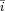 ki,max = μai,max *a (where k and a respectively denote the size of kimberlite and alluvial deposits in a cell), and that a minimal level of investment
ki,max = μai,max *a (where k and a respectively denote the size of kimberlite and alluvial deposits in a cell), and that a minimal level of investment 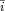 ki,min = μki,min * k,
ki,min = μki,min * k, 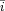 = μai,min* a is required to generate revenue. That is, we assume that minimum and maximum investment for the extraction of kimberlite diamonds exceeds that for alluvial diamonds, i.e. μki,max > μai,max and μki,min > μai,min, and that investment in industrial diamond production is limited to Ȧ, although Ḃ can profit from previous government investment when it assumes control of a cell. Note also that investment in artisanal and agricultural production is not bounded and does not require a minimum level to generate revenue.
= μai,min* a is required to generate revenue. That is, we assume that minimum and maximum investment for the extraction of kimberlite diamonds exceeds that for alluvial diamonds, i.e. μki,max > μai,max and μki,min > μai,min, and that investment in industrial diamond production is limited to Ȧ, although Ḃ can profit from previous government investment when it assumes control of a cell. Note also that investment in artisanal and agricultural production is not bounded and does not require a minimum level to generate revenue.

where ρ is a constant that defines the yield from industrial production. Revenue generated by artisanal alluvial diamond production is given by:
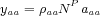
where ρaa is a constant defining the yield from artisanal alluvial production, NP denotes the number of peasants in a cell, and aaa = a - aai, with aai = 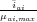 . And lastly, revenue generated by agricultural production is given by:
. And lastly, revenue generated by agricultural production is given by:
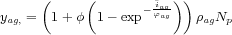
and where ρag is the productivity of the peasants, NP denotes the number of peasants in a cell, φ is the maximum increase in productivity generated by investment, and φag is a scaling factor that determines the requisite level of investment for a given level of revenue. Due to the highly organized and controlled process of diamond mining in industrial production, we assume that the leader in control is the sole recipient of revenue from all industrial production (ski = 1 and sai = 1). Turning to artisanal extraction and agriculture, we specify saa and sag as increasing with investment in each sector, and assume that in the absence of investment, the minimum share of revenue going to Ȧ,Ḃ is given by saa,min, sag,min, and the maximum share by saa,max, sag,max:
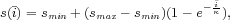
where 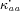 and
and 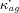 are scaling factors that determine the requisite level of investment for a given share. Note that while investment in the artisanal sector has no direct influence on total revenue, it does affect the ability of Ȧ,Ḃ to tax peasant revenue.
are scaling factors that determine the requisite level of investment for a given share. Note that while investment in the artisanal sector has no direct influence on total revenue, it does affect the ability of Ȧ,Ḃ to tax peasant revenue.
Table A1. Agent Strategies

Table A2. Control Strategy Parameters

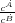 and and modify this ratio by adding the term υcNP (where NP is the number of peasants in the cell and υC is a constant:
and and modify this ratio by adding the term υcNP (where NP is the number of peasants in the cell and υC is a constant:
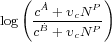
As a result, the cost of shifting control increases with the size of the cell's peasant population. Next, we add  P to account for the influence of aggregate peasant sympathy on the balance of power in a cell, and ηc
P to account for the influence of aggregate peasant sympathy on the balance of power in a cell, and ηc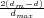 to measure the effect of geography (where d is the distance from the cell to the capital city, dm is the distance to the midpoint between the capital and the border, and dmax is the distance between a border cell and the capital), to obtain:
to measure the effect of geography (where d is the distance from the cell to the capital city, dm is the distance to the midpoint between the capital and the border, and dmax is the distance between a border cell and the capital), to obtain:
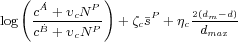
where ζc weights the influence of the peasant sympathy and ηc the influence of the geography. The logistic transformation (since we define qc ∈ [-10, 10]) yields:
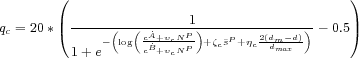
Note that conflict in a grid cell makes it impossible for either agent to control this cell.
1We gratefully acknowledge comments from Lars Erik Cederman, Chanan Cohen, Nils Petter Gleditsch, Kristian Skrede Gleditsch, Havard Herge, Simon Hug, Eric Little, Ian Lustick, Stathis Kalyvas, Rick Riolo, Nils Weidmann, and participants at seminars organized by the Peace Research Institute Oslo, Center for International Studies at the Swiss Federal Institute of Technology, the University of Michigan's Center for the Study of Complex Systems, the Political Science Department at Michigan State University, and the University of Essex. We also remain indebted to three anonymous reviewers for their comments. Support for this work was provided by the Hebrew University Intramural Research Fund, the Israeli National Science Foundation, and the Department of Political Science at Michigan State University. Additional research assistance with model development was provided by Michael Bommarito II. All faults remain our own.
2 A quote from Ross (2006: 265) is instructive: "Studies of natural resource wealth and civil war have been hampered by measurement error, endogeneity, lack of robustness, and uncertainty about causal mechanisms."
3 For a detailed discussion of conflicting results on the resource-civil war relationship, see Ross (2004).
4 See Humphreys 2005 for a discussion of plausible mechanisms underlying the resource-civil war relationship.
5 For a comparison of exploratory and consolidative modeling see Bankes 2002.
6 For a discussion of research strategies using ABM see Lustick and Miodownik (forthcoming).
7 The capital city differs from other cells in the landscape given that it serves as a reference point for the government: as the government seeks to control territory further away from the capital city, the cost of control increases monotonically.
8 In the description that follows, we use notation consistent with the existence of two ethic groups, with the exception of Demonstration Run I, in which all agents belong to a single ethnic group and where we refer to discontented members (co-ethnics) who seek to overthrow the government as rebels.
9 The nature of the resource base has implications for investment and revenue, as well as territorial control. Alluvial diamonds, for instance, are considered "lootable" in that they constitute high value goods with low economic barriers to entry - their extraction by difficult-to-tax artisans requires little in the way of investment and makes it difficult for the state to establish monopoly control over these resources. In contrast, non-lootable resources such as kimberlite or deep-shaft diamonds have high economic barriers to entry - large amounts of capital and technology are required to exploit them profitably, forming a natural barrier that excludes small-scale artisanal miners and makes it easier for the state to establish monopoly control over the resource (by eliminating the need to invest in coercive capacity to deter wildcat miners). Closely tied to the mode of extraction is the location of resource deposits, and we currently distinguish between "point-source" and "diffuse" resource distributions. For more on the resource profiles of alluvial and kimberlite diamonds, their modes of extraction, and implications for civil war, see Snyder and Bhavnani 2005. Note that while we limit our initial focus to agrarian and diamond economies, REsCape may be modified to account for the revenue opportunity structures of other resources such as oil and timber.
10 Peasant revenue from social welfare yswP is a function of the importance of the cell, and difference between actual and maximal levels of peasant support. We provide additional detail in our discussion of spending strategies in the Appendix.
11 We seek to avoid the possibility of negative ethnic salience, in the event that relative economic well-being is very high. See the Appendix for additional details on our calculation of ethnic salience.
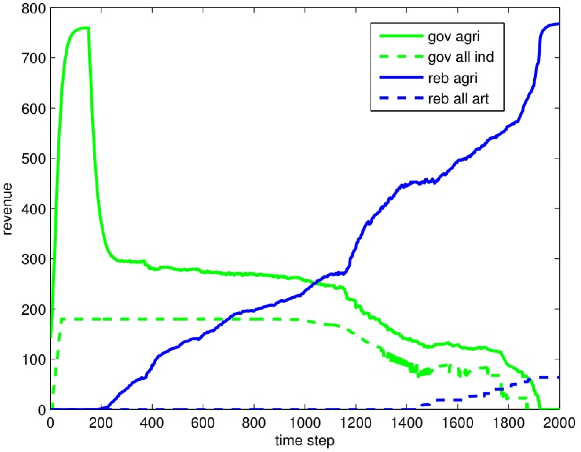
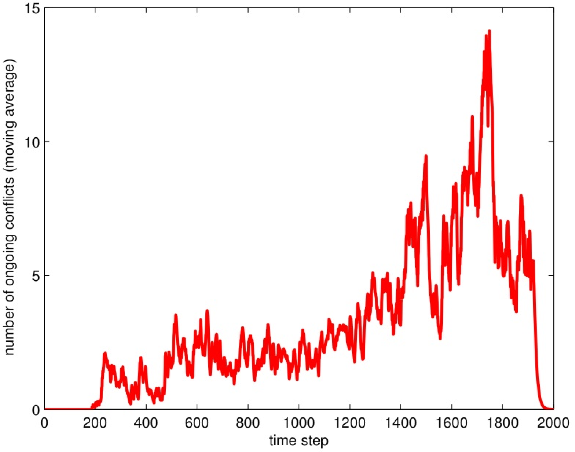
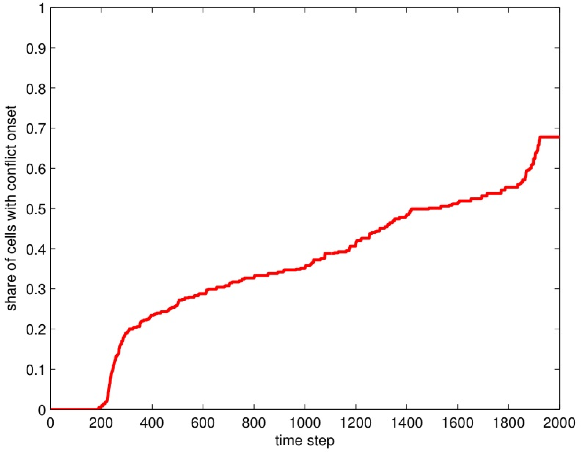
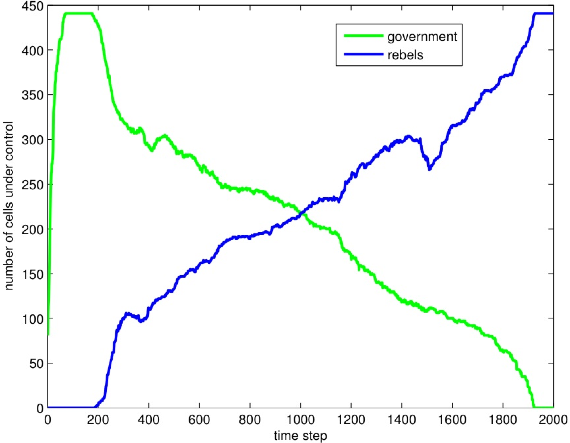
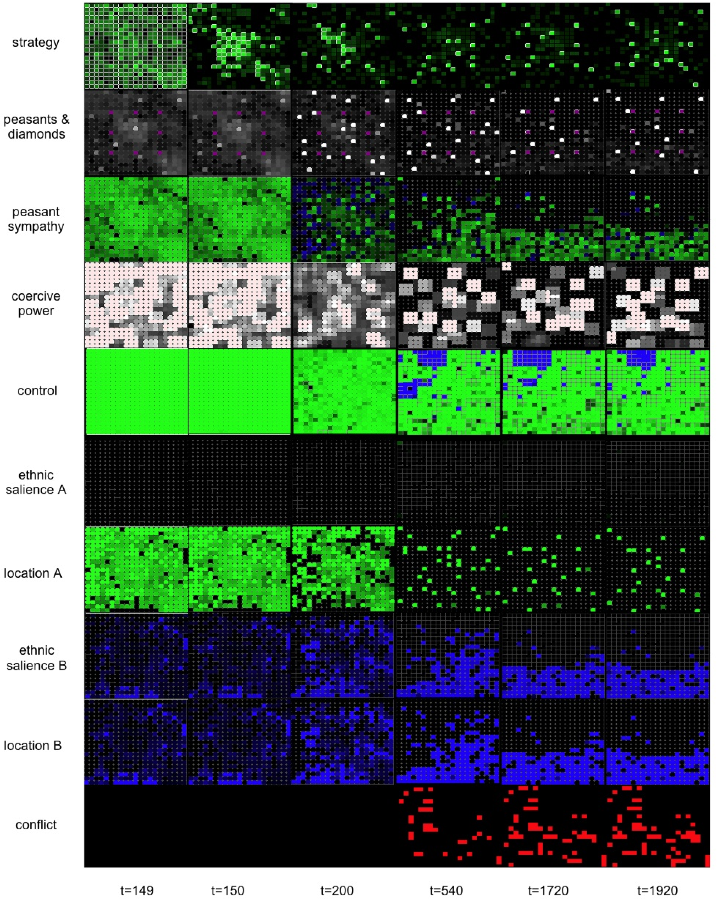
12 Our selection of snapshots was designed to capture steps during which critical developments occurred.
13 Note that our framework restricts rebel investment in industrial mining.
14 Note that the pockets of the landscape under Ḃ's control in the north of the landscape are a "legacy of the past" in that these are cells that flipped to Ḃ's control but were abandoned shortly thereafter. Given that they remain unpopulated, control never shifts back to the government.
AXELROD R (1997) "Advancing the Art of Simulation in the Social Sciences." In Conte, R., Hegselmann, R., and Terna, P. (eds.) Simulating Social Phenomena (Lecture Notes in Economics and Mathematical Systems), Berlin: Springer-Verlag.
AXELROD R and Cohen, M D (2001) Harnessing Complexity: Organizational Implications of a Scientific Frontier, Chicago: The Free Press.
BANKES S C (2002) "Tools and Techniques for Developing Policies for Complex and Uncertain Systems." Proceedings of the National Academy of Sciences of the United States of America, 99, pp. 7263-7266.
BHAVNANI R and Miodownik D (2008a) "Ethnic Polarization, Ethnic Salience, and Civil War." In Progress.
BHAVNANI R and Miodownik D (2008b) "Ethnic Minority Domination and Civil War." In Progress.
BONABEAU E (2002) "Agent-Based Modeling: Methods and Techniques for Simulating Human Systems." Proceedings of the National Academy of Sciences of the United States of America, 99, pp. 7280-7287.
BUHAUG H and Gates S (2002) "The Geography of Civil War." Journal of Peace Research, 39(4), pp. 417-433.
CEDERMAN L-E and Girardin L (2007) "Beyond Fractionalization: Mapping Ethnicity onto Nationalist Insurgencies." American Political Science Review, 101(1), pp. 173-185.
COLLIER P and Hoeffler A (1998). "On Economic Causes of Civil War.'' Oxford Economic Papers, 50(4):563-573.
COLLIER P and Hoeffler A (2004) "Greed and Grievance in Civil War." Oxford Economic Papers, 56(4), pp. 563-595.
COLLIER P and Hoeffler A (2005) "The Political Economy of Secession." In Hannum H and Babbit E F (eds), Negotiating Self-Determination. Lexington Books, Lanham MD.
CONTE R, Hegselmann R, and Terna P (1997) Simulating Social Phenomena. Lecture Notes in Economics and Mathematical Systems. Springer.
DOYLE M W and Sambanis N (2000) "International Peacebuilding: A Theoretical and Quantitative Analysis." American Political Science Review, 94(4), pp. 779-801.
ELBADAWI I and Sambanis N (2002) "How Much War Will We See? Explaining the Prevalence of Civil War." Journal of Conflict Resolution, 46(3), pp. 307-334.
FEARON J D and Laitin D D (2003) "Ethnicity, Insurgency, and Civil War." American Political Science Review, 97(1), pp. 75-90.
FEARON J D, Kasara K, and Laitin D D (2007) "Ethnic Minority Rule and Civil War Onset." American Political Science Review, 101(1), pp. 187-193.
GATES S (2002) "Recruitment and Allegiance: The Microfoundations of Rebellion." Journal of Conflict Resolution, 46, pp. 111-130.
HEGRE H (2002) "Some Social Requisites of a Democratic Civil Peace: Democracy, Development, and Armed Conflict." Paper presented to the Annual Meeting of the American Political Science Association, Boston, MA, 29 August-1 September.
HEGRE H and Sambanis N (2006) "Sensitivity Analysis of the Empirical Literature on Civil War Onset." Journal of Conflict Resolution, 50, pp. 508-535.
HUMPHREYS M (2005) "Natural Resources, Conflict, and Conflict Resolution: Uncovering the Mechanisms". Journal of Conflict Resolution, 49(4), pp.508-537.
LUJALA P, Gleditsch N P, and Gilmore E (2005) "A Diamond Curse?: Civil War and a Lootable Resource." Journal of Conflict Resolution, 49(4), pp. 538-562.
LUSTICK I S, Miodownik D (forthcoming) "Abstractions, Ensembles, and Virtualizations: Simplicity and Complexity in Agent-Based Modeling." Comparative Politics.
MEYER A D, Gaba V, and Colwell K A (2005) "Organizing Far from Equilibrium: Non-Linear Change in Organizational Fields." Organization Science, 16(5), pp. 456-473.
MONTALVO, J G and Reynal-Querol M (2005) "Ethnic Polarization, Potential Conflict, and Civil Wars." The American Economic Review, 95(3), pp. 796-816.
PARUNAK H V D, Savit R, and Riolo R L (1998) "Agent-Based Modeling vs. Equation-Based Modeling: A Case Study and Users' Guide." In Workshop on Multi-Agent Systems and Agent-Based Simulation, Springer, pp. 10-25.
REYNAL-QUEROL M (2002) "Ethnicity, Political Systems, and Civil Wars." Journal of Conflict Resolution, 46(1), pp. 29-54.
ROSS M L (2004) "What Do We Know about Natural Resources and Civil War?" Journal of Peace Research, 41(3), pp. 337-356.
ROSS M (2006) "A Closer Look at Oil, Diamonds, and Civil War." Annual Review of Political Science, 9, pp. 265-300.
SAMBANIS N (2001) "Do Ethnic and Nonethnic Civil Wars Have the Same Causes? A Theoretical and Empirical Inquiry (Part 1)." Journal of Conflict Resolution, 45(3), pp. 259-282.
SNYDER R and Bhavnani R (2005) "Blood, Diamonds, and Taxes: Lootable Wealth and Political Order in Sub-Saharan Africa." Journal of Conflict Resolution, 49(4), pp.563-597.
WIMMER A, Cederman L-E, and Min B (2007) "Ethnic Politics and Violent Conflicts, 1946-2005: A Configurational Approach." Paper presented at the conference Disaggregating the Study of Civil War and Transnational Violence, University of Essex, 24-25 November 2007.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]