Xavier Vilà (2008)
A Model-To-Model Analysis of Bertrand Competition
Journal of Artificial Societies and Social Simulation
vol. 11, no. 2 11
<https://www.jasss.org/11/2/11.html>
For information about citing this article, click here
Received: 04-Aug-2007 Accepted: 16-Mar-2008 Published: 31-Mar-2008
 Abstract
Abstract
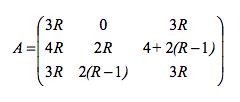
|
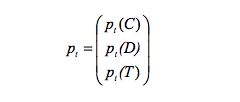
|
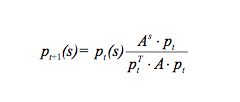
|
where As denotes the row of A corresponding to the strategy s.
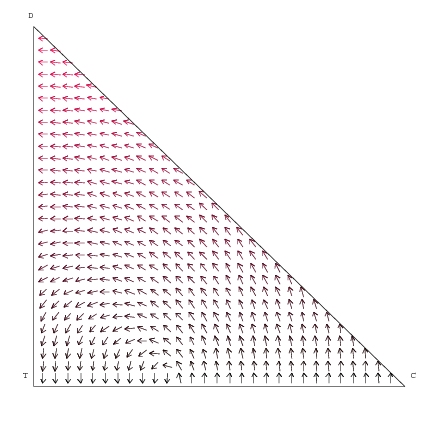
|
| Figure 1. Vector Field with non-loyal consumers |

|
| Figure 2. Vector Field with loyal consumers |
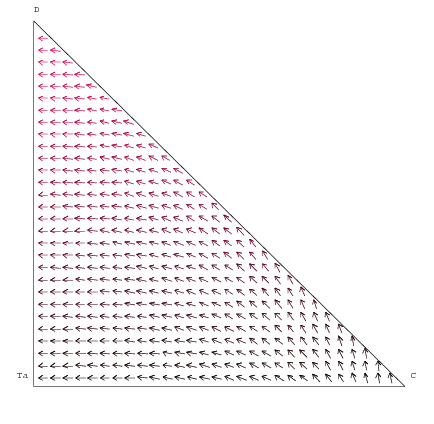
|
| Figure 3. Vector Field with loyal consumers (and Tat for Tit) |
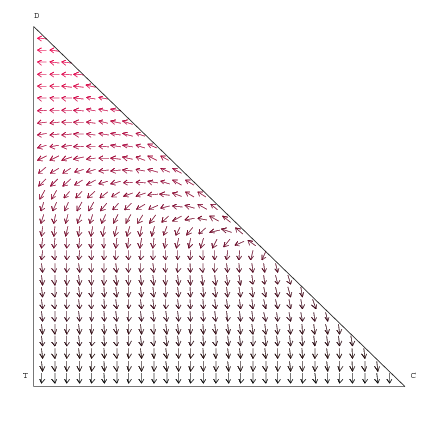
|
| Figure 4. Vector Field with non-loyal consumers |

|
| Figure 5. Vector Field with loyal consumers |
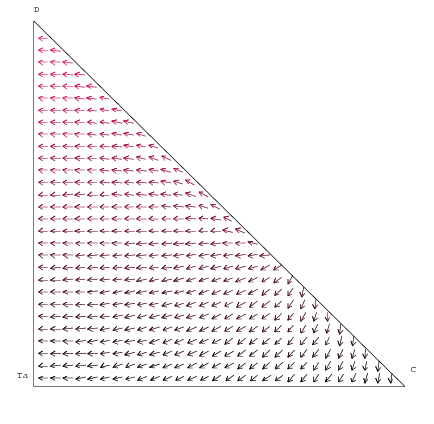
|
| Figure 6. Vector Field with loyal consumers (and Tat for Tit) |
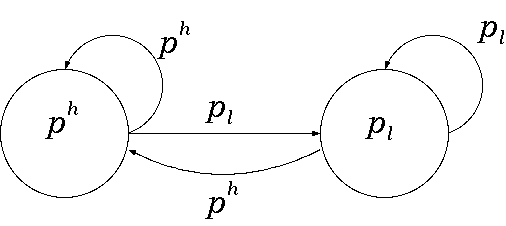
|
| Figure 7. The Tit for Tat automaton |
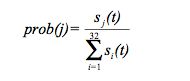
|
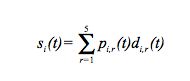
|
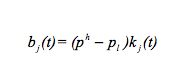
|
| Automata 1: 0 0 0 0 1 1 1 | Automata 2: 1 1 0 0 0 1 1 |
| Automata 1: 0 1 0 0 0 1 1 | Automata 2: 1 0 0 0 1 1 1 |
| Tit for Tat: 0 1 1 0 0 1 0 | Always low price: 1 0 0 0 1 1 1 |
| Tit for Tat: 1 0 0 1 1 0 1 | Always low price: 0 1 0 0 0 1 1 |
|
|
|
|
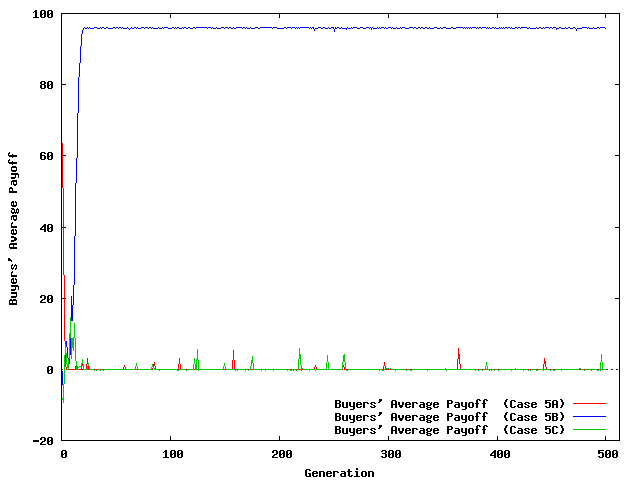
|
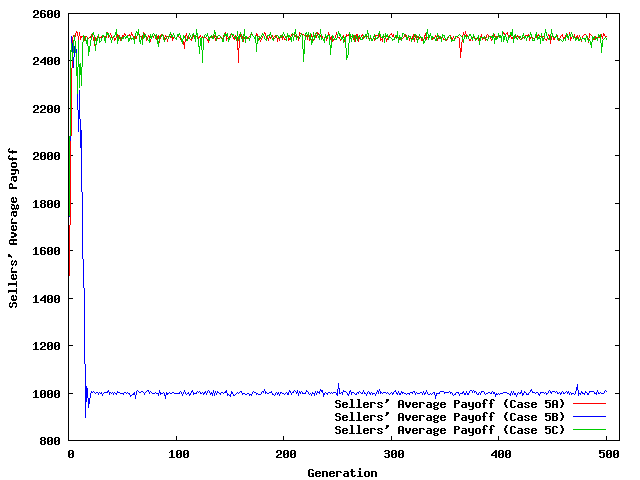
|
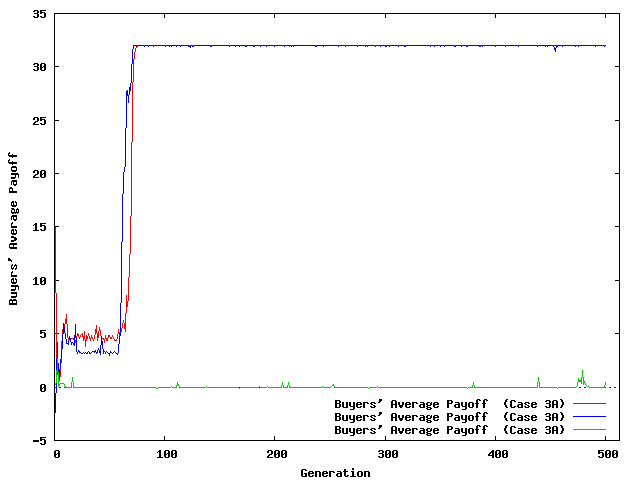
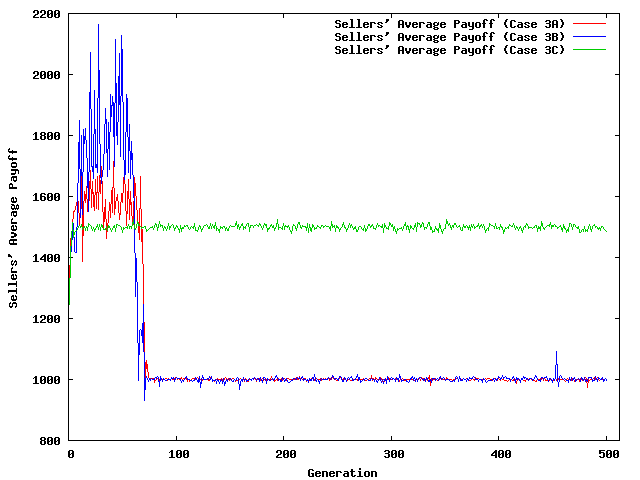
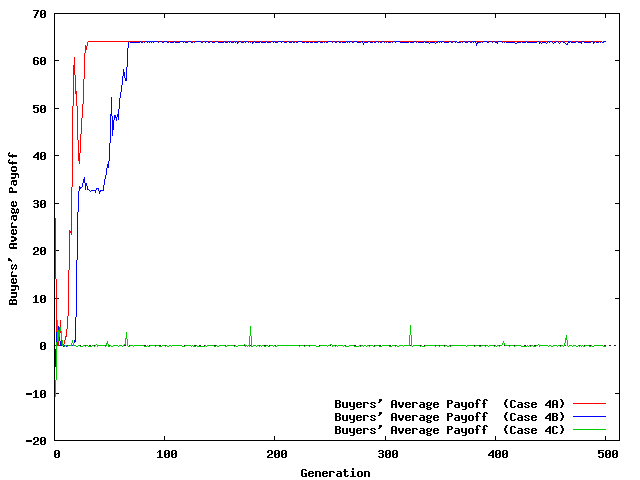
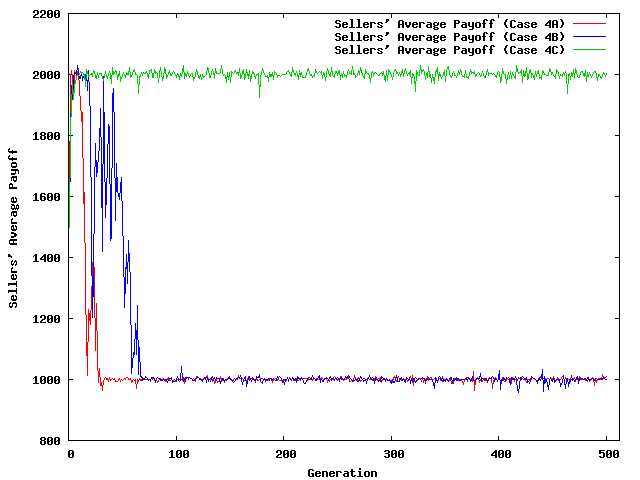
| Figure 8. Evolution of Average Payoffs | |
BINMORE, K. and Samuelson, L. (1992). Evolutionary Stability in Repeated Games Played by Finite Automata. Journal of Economic Theory, 57(2). pp. 278-305.
BERTRAND, J. (1883). Book review of theorie mathematique de la richesse sociale and of recherches sur les principles mathematiques de la theorie des richesses. Journal de Savants, 67. pp. 499-508.
DENECKERE, R., Kovenock, D., and Lee, R. (1992). A Model of Price Leadership Based on Consumer Loyalty. Journal of Industrial Economics, 40(2). pp. 147-56.
DUDEY, M. (1992). Dynamic Edgeworth-Bertrand Competition. The Quarterly Journal of Economics, 107(4). pp. 1461-1477.
DUTTA, P., Matros, A., and Weibull, J.W. (2007). Long-Run Price Competition. RAND Journal of Economics, 38(2). pp. 291-313.
FERDINANDOVA, I. (2003). On the Influence of Consumers' Habits on Market Structure. Mimeo. Universitat Autònoma de Barcelona.
HALES, D., Rouchier, J, and Edmonds, B. (2003). Model-to-Model Analysis. Journal of Artificial Societies and Social Simulation , 6(4)5. https://www.jasss.org/6/4/5.html
HARRINGTON, J. E. and Chang, M.H. (2005). Co-Evolution of Firms and Consumers and the Implications for Market Dominance. Journal of Economic Dynamics and Control, 29(1-2). pp. 245-276.
HEHENKAMP, B. (2002). Sluggish Consumers: An Evolutionary Solution to the Bertrand Paradox. Games and Economic Behavior, 40. pp. 44-76.
HEHENKAMP, B. and Leininger, W. (1999). A note on evolutionary stability of Bertrand equilibrium. Journal of Evolutionary Economics, 9. pp. 367-371.
MAYNARD SMITH, J. (1982). Evolution and the Theory of Games. Cambridge University Press, Cambridge.
MILLER, J. H. (1996). The coevolution of automata in the repeated Prisoner's Dilemma. Journal of Economic Behavior and Organization, 29(1). pp. 87-112.
NOWAK, M. A., Sasaki, A., Taylor, C., and Fudenberg, D. (2004). Emergence of cooperation and evolutionary stability in finite populations. Nature, 428(6983). pp. 646 - 650.
VILÀ, X. (1997). "Adaptive Artificial Agents Play a Finitely Repeated Discrete Principal-Agent Game". In Conte, R., Hegselmann, R., and Terna, P., (Eds.). Simulating Social Phenomena, volume 456 of Lecture Notes in Economics and Mathematical Systems, Springer-Verlag. pp. 437-456.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]