Marc R.H. Roedenbeck and Barnas Nothnagel (2008)
Rethinking Lock-in and Locking: Adopters Facing Network Effects
Journal of Artificial Societies and Social Simulation
vol. 11, no. 1 4
<https://www.jasss.org/11/1/4.html>
For information about citing this article, click here
Received: 25-Apr-2007 Accepted: 08-Nov-2007 Published: 31-Jan-2008
 Abstract
Abstract Arthur’s Model of Path Dependence
Arthur’s Model of Path Dependence
//Initializing the Stacks |
| Code 1. Random walk |
| This pseudo code represents a snippet from the full program only
(lines 339-435); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
 |
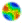
| Figure 1. Adopter difference of random walk |
 |
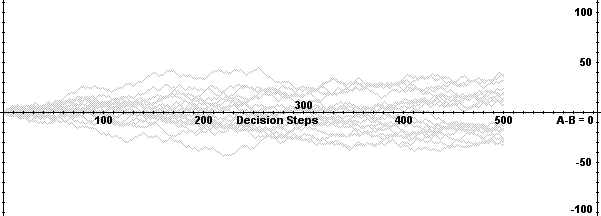
| Figure 2. Market share distribution of random walk |
//Initializing the Stacks |
| Code 2. Random walk with absorbing barrier |
| This pseudo code represents a snippet from the full program only
(lines 339-435); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
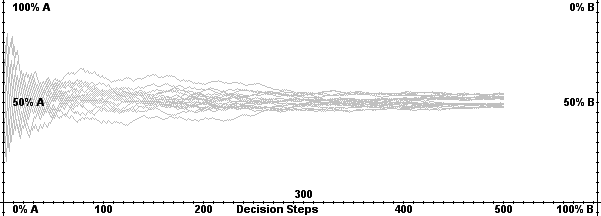
 |
| Figure 3. Adopter difference of random walk with absorbing barrier |
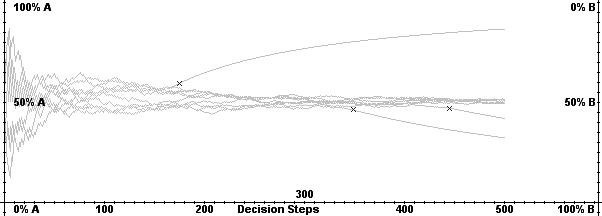 |
| Figure 4. Market share distribution of random walk with absorbing barrier |
//Initializing the Stacks |
| Code 3. Polya urn process |
| This pseudo code represents a snippet from the full program only
(lines 438-501); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
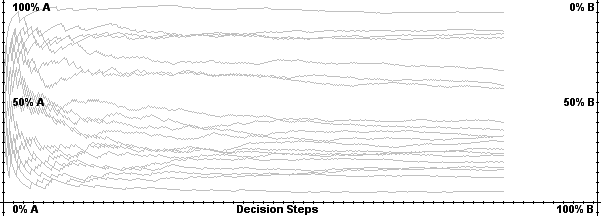 |
| Figure 5. Market share distribution of the Polya urn process |
| |||||||||
| Table 1. Arthurian agents with network effects |
//Initializing the Stacks |
| Code 4. Arthur’s simple model |
| This pseudo code represents a snippet from the full program only
(lines 503-630); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
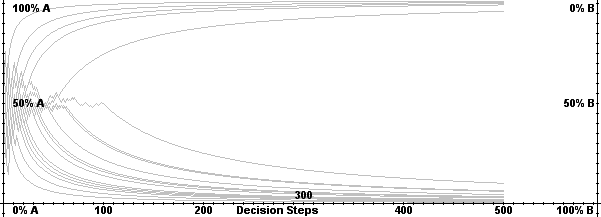 |
| Figure 6. Market share distribution of Arthur’s urn process |
 Limits of Arthur’s Simple Model and his Advanced Extensions
Limits of Arthur’s Simple Model and his Advanced Extensions Modification of Arthur’s Urn Model
Modification of Arthur’s Urn Model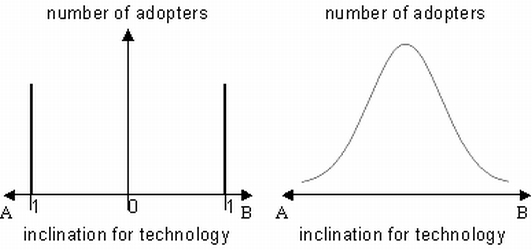 |
| Figure 7. Frequency distribution of Arthur (1989) and the new model |
| ||||||
| Table 2. Gaussian distributed actors for two technologies |
function gauss() { |
| Code 5. Reflexive Gaussian distributed actor |
| This pseudo code represents a snippet from the full program only
(lines 128-135); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
//weighted indirect network effects for A |
| Code 7. Indirect network effects |
| This pseudo code represents a snippet from the full program only
(lines 693-695); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
| ||||||
| Table 3. Gaussian distributed actors for two technologies with direct and indirect network effects |
| c(n) = n (n-1) / 2 | (1) |
//weighted direct network effects for A |
| Code 8. Direct network effects |
| This pseudo code represents a snippet from the full program only
(lines 697-699); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
//calculate the utility difference for one adopter for both technologies |
| Code 9. Decision rule depending on difference between utilitys |
| This pseudo code represents a snippet from the full program only
(lines 701-714); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
| ||||||
| Table 4. Gaussian distributed actors for two technologies with weighted direct and indirect network effects |
| f_logit(x) = G / [1 + e^( k * (a - x) ) ] | (2) |
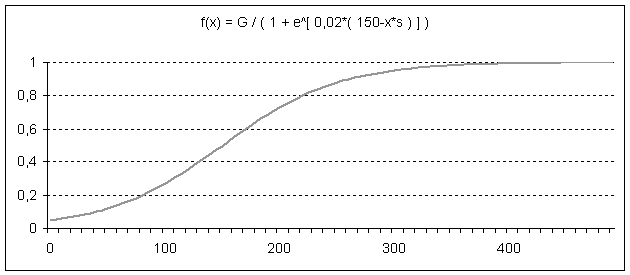 |
| Figure 8. Smooth logistic information diffusion for indirect network effects |
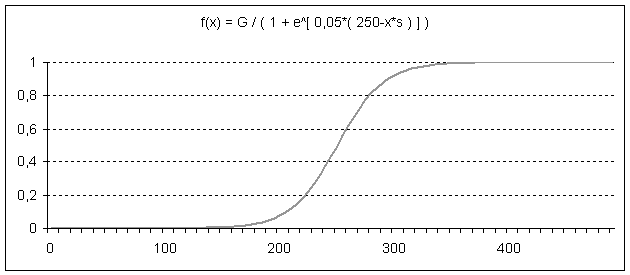 |
| Figure 9. Sharp logistic information diffusion for direct network effects |
| ||||||
| Table 5. Gaussian distributed actors for two technologies with modified weighted direct and indirect network effects |
// Calculate logistic y-value |
| Code 10. Logistic function |
| This pseudo code represents a snippet from the full program only
(lines 123-126); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
//calculating weighted indirect network effects |
| Code 11. Modified indirect and direct network effects |
| This pseudo code represents a snippet from the full program only
(lines 693-699); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
 |
| Figure 10. Distribution with Gaussian adopter, indirect, and direct network effects |
//Initialize help |
| Code 12. Lock-in calculation |
| This pseudo code represents a snippet from the full program only
(lines 721-765); a complete version (with PHP/Winbinder) may be downloaded from here and run under Windows |
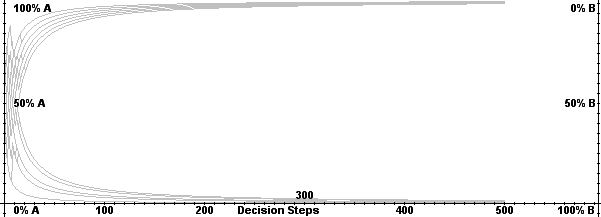
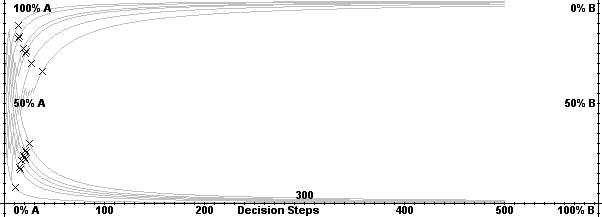 |
| Figure 11. Lock-in function for 20 simulations |
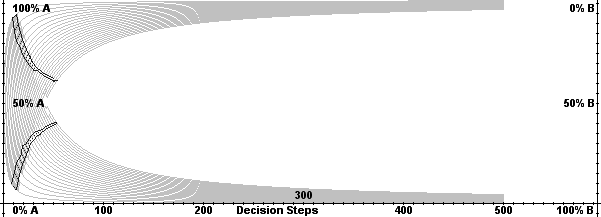 |
| Figure 12. Lock-in band for 10.000 simulations |
 Results and Discussion
Results and Discussion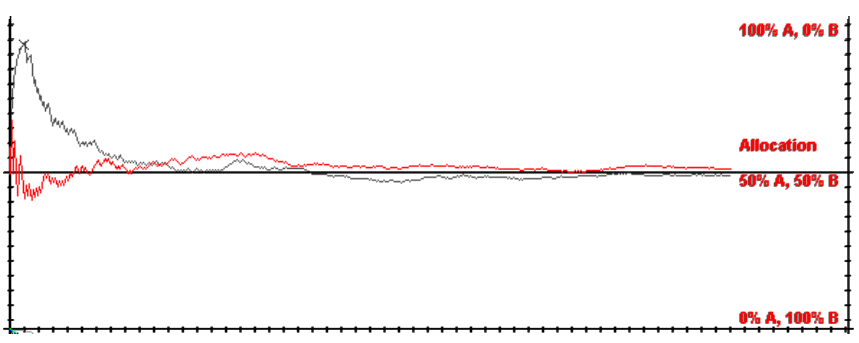 |
| Figure 13. Arthurian and Extended Model without Returns from Lock-in |
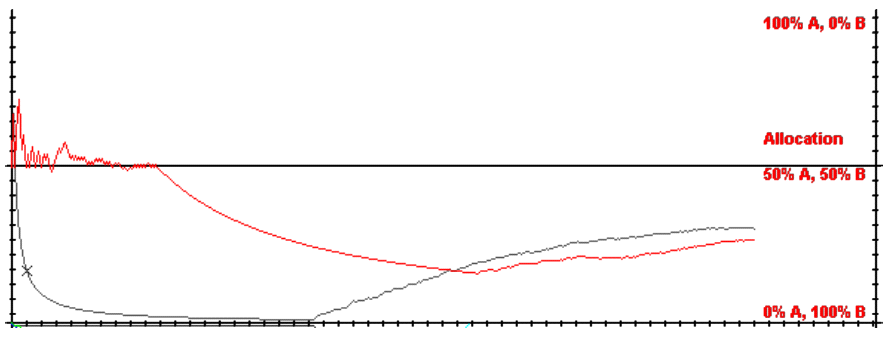 |
| Figure 14. Arthurian and Extended Model with Randomly Dropped Returns |
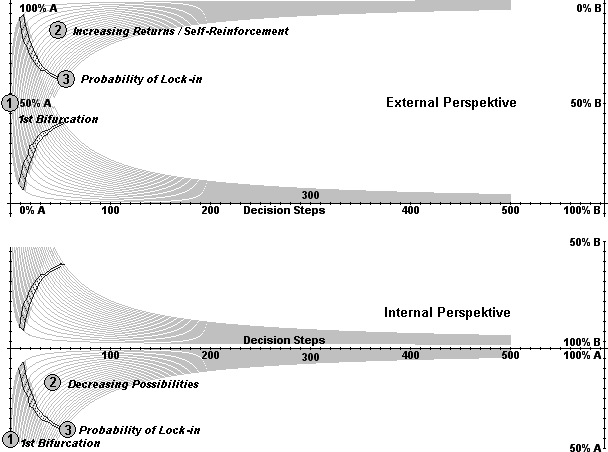 |
| Figure 15. New Model for Empirical Research |
ACKERMANN R (2001) Pfadabhängigkeit, Institutionen und Regelreform. Tübingen: J. C. B. Mohr (Paul Siebeck).
ARROW K J (2004) Path dependence and economic equilibrium. In Guinnane T W, Sundstrom W A & Whatley W (Eds.). History matters. Essays on economic growth, technology, and demographic change, Stanford: Stanford University Press.
ARTHUR W B (1988) Self-Reinforcing Mechanisms in Economics. In Pines D (Ed.). The Economy as an Evolving Complex System, Reading, MA: Addison-Wesley.
ARTHUR W B (1989) Competing Technologies, Increasing Returns, and Lock-In by Historical Events. Economic Journal, 99. pp. 116-131.
ARTHUR W B (1994) Increasing Returns and Path Dependence in the Economy. Ann Arbor: University of Michigan Press.
ARTHUR W B (1996) Increasing Returns and the New World of Business. Harvard Business Review, July-Aug., pp. 1-10.
ARTHUR W B, Ermoliev Y M & Kaniovski Y M (1983) On Generalized Urn Schemes of the Polya Kind. Kibernetika, 19(1), pp. 49-56.
ARTHUR W B, Ermoliev Y M & Kaniovski Y M (1985) Strong Laws for a Class of Path-Dependent Urn Processes. Paper presented at the: International Conference on Stochastic Optimization, Kiev.
BASS F M (1969) A New Product Growth Model for Consumer Durables. Management Science, 15, pp. 215-227.
BEYER J (2005) Pfadabhängigkeit ist nicht gleich Pfadabhängigkeit! - Wider den impliziten Konservativimus eines gängigen Konzeptes. Zeitschrift für Soziologie, 34(1), pp. 5-21.
BOX G E P & Muller M E (1958) A note on the generation of random normal deviates. The Annals of Mathematical Statistics, 29(2), pp. 610-611.
BRITTON J N H (2004) The Path Dependence of Multimedia: Explaining Toronto’s Cluster. Working Paper - 6th Annual ISRN National Meeting, pp. 13.
BRUGGEMANN D (2002) NASA: a path dependent organization. Technology in Society, 24, pp. 415-431.
CALDAS J C & Coelho H (1999) The Origin of Institutions: socio-economic processes, choice, norms and conventions. Journal of Artificial Societies and Social Simulation, 2(2), https://www.jasss.org/2/2/1.html
COWAN R & Gunby P (1996) Sprayed to Death: Path Dependence, Lock-in and Pest Control Strategies. The Economic Journal, 106(436), pp. 521-542.
DAVID P A (1985) Clio and the Economics of QWERTY. American Economic Review, 75(2), pp. 332-337.
DODSON J A & Muller E (1978) Models of New Product Diffusion Through Advertising And Word-of-Mouth. Management Science, 24(15), pp. 1568-1578.
GARUD R & Karnøe P (2001) Path creation as a process of mindful deviation. In Garud R & Karnøe P (Eds.). Path Dependence and Creation, London: Lawrence Erlbaum Associates.
GARUD R & Karne P (2003) Bricolage vs. breakthrough: Distributed and embedded agency in technology entrepreneurship. Research Policy, 32(2), pp. 277-300.
GOMPERTZ B (1825) On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies. Philosophical Transactions of the Royal Society of London, 115, pp. 513-585.
HELFAT C E (1994) Evolutionary trajectories in petroleum firm R&D. Management Science, 40(12), pp. 1720-1747.
HÄRTTER E (1974) Wahrscheinlichkeitsrechnung für Wirtschafts- und Naturwissenschaftler. Göttingen, Vandenhoeck & Ruprecht.
HERRMANN-PILLATH C (2002) Grundriß der Evolutionsökonomik. München: UTB-Wilhelm Fink Verlag.
KEMP J (1999) Spontaneous Change, Unpredictability and Consumption Externalities. Journal of Artificial Societies and Social Simulation, 2(3), https://www.jasss.org/2/3/1.html
LEYDESDORFF L & Besselaar P V d (1998) Competing Technologies: Lock-ins and Lock-outs. In Dubois D (Ed.). Computing Anticipative Systems, New York: National Academy of Physics.
LEYDESDORFF L (2000) The triple helix: an evolutionary model of innovations Research Policy, 29(2000), pp. 243-255.
LEYDESDORFF L (2001) Technology and Culture: The Dissemination and the Potential ’Lock-in’ of New Technologies. Journal of Artificial Societies and Social Simulation, 4(3), https://www.jasss.org/4/3/5.html
LIEBOWITZ S J & Margolis S E (1990) The Fable of the Keys. Journal of Law and Economics, 33, pp. 1-26.
LIEBOWITZ S J & Margolis S E (1995) Path Dependence, Lock-In, and History. Journal of Law, Economics and Organization, 11(1), pp. 205-226.
LIEBOWITZ S J & Margolis S E (2001) The Fable of the Keys. In Margolis S E (Ed.). Winners, Losers & Microsoft. Competition and Antitrust in High Technology, Oakland: The Independent Institute.
LORENZ E N (1963) Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences, 20(2), pp. 130-141.
MAHONEY J (2000) Path Dependence in Historical Sociology. Theory and Society, 29(4), pp. 507-548.
MALERBA F, Nelson R, Orsenigo L & Winter S (2001) History-Friendly models: An overview of the case of the Computer Industry, Journal of Artificial Societies and Social Simulation, 4(3), https://www.jasss.org/4/3/6.html
NEUMANN J v & Morgenstern O (2004 [1944]) Theory of Games and Economic Behavior. Princeton, NJ: University Press.
NORTH D C (1990) Institutions, Institutional Change and Economic Performance. Cambridge, MA: Cambridge University Press.
PUFFERT D J (2002) Path Dependence in Spatial Networks: The Standardization of Railway Track Gauge. Explorations in Economic History, 39, pp. 282-314.
RICO A, Costa-Font & Power J (2005) Rather Power Than Path Dependency? The Dynamics of Institutional Change under Health Care Federalism. Journal of Health Politics, Policy and Law, 30(1-2), pp. 231-252.
ROEDENBECK M R H, Strobel J C & Tepe M (2005) ’Walking through the Path-Dice: How to Measure the Single Phases of Path Dependency’ Paper presented at the: Measuring Path Dependency - The Social-Constructivist Challenge, Freie Universität Berlin, Berlin, Germany.
ROGERS E M (1983) Diffusions of Innovations. New York, London: The Free Press.
SAHAL D (1981) Patterns of technological innovation. London et al.: Addison-Wesley.
SCHREYÖGG G, Sydow J & Koch J (2003) "Organisatorische Pfade - Von der Pfadabhängigkeit zur Pfadkreation". In Sydow J (Ed.). Managementforschung 13: Strategische Prozesse und Pfade, Wiesbaden.
STERMAN J D (2000) "Path Dependency and Positive Feedback". Business Dynamics, Boston: McGraw Hill.
STROBEL J C & Roedenbeck M R H. 2006. ’How to Shape Markets for Fuel-Efficient Automobiles? Lessons from the Success-Story of Diesel Cars in Germany.’ Paper presented at the: 22nd EGOS Colloquium, Bergen, Norway.
SYDOW J, Schreyögg G & Koch J. 2005. ’Organizational Paths: Path Dependency and Beyond.’ Paper presented at the: 21st EGOS Colloquium, Berlin, Germany.
VERHULST P F (1838) ’Notice sur la loi que la population suit dans son accroissement’. Correspondance mathÈmatique et physique, 10, pp. 113-121.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]