Guido Fioretti and Alessandro Lomi (2008)
An Agent-Based Representation of the Garbage Can Model of Organizational Choice
Journal of Artificial Societies and Social Simulation
vol. 11, no. 1 1
<https://www.jasss.org/11/1/1.html>
For information about citing this article, click here
Received: 17-Feb-2007 Accepted: 28-Sep-2007 Published: 31-Jan-2008
 Abstract
Abstract
|
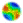
| Figure 1. The flow chart of the GCM: resolutions and oversights mark the end of decision-making, flights make it start again |
|
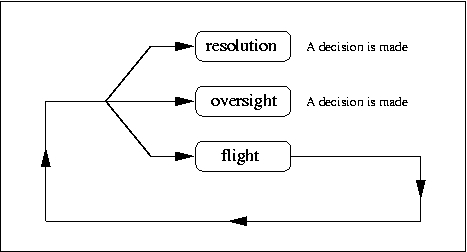
| Figure 2. The decision structure can either be non-segmented (left), hierarchical (centre) or specialized (right). In the matrices a "1" indicates that the row element has access to the column element |
|
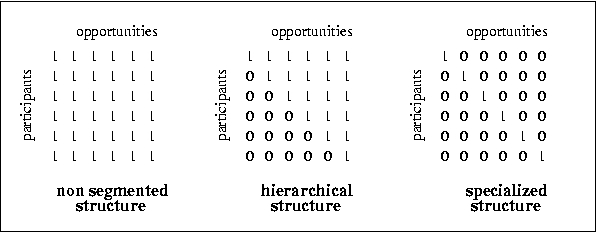
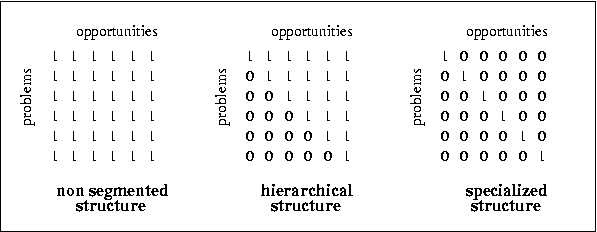
| Figure 3. The access structure can either be non-segmented (left), hierarchical (centre) or specialized (right). In the matrices a "1" indicates that the row element has access to the column element |
| XERC(i) ≤ XEE(i) | (1) |
| XERC(i) = XERC(i) + XERP(j) | (2) |
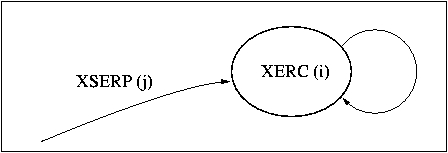
|
| Figure 4. The energy required at the i-th opportunity is the sum of the energies of the problems that impinge on it |
| XEE(i) = XEE(i) + XSC(lt) * XEA(k, lt) | (3) |
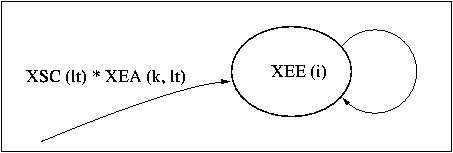
|
| Figure 5. The energy that can be expended at the i-th opportunity is the sum of the energies of the participants that attend it |
| s = XERC(i) - XEE(i) | (4) |

|
| Figure 6. The parameters that regulate the entry and exit of agents. Initial number, exogenous flows, interruption of exogenous flows, and exit of agents once they have been involved in decision-making |
|
|
| Figure 7. The buttons that select the decision structure (left) and the access structure (right). Non-segmented structures are denoted by 0, hierarchical structures are denoted by 1, specialized structures are denoted by 2 |

|
| Figure 8. The buttons that specify the energy distribution, its minimum and maximum values and whether the energy values are shown aside the agents |
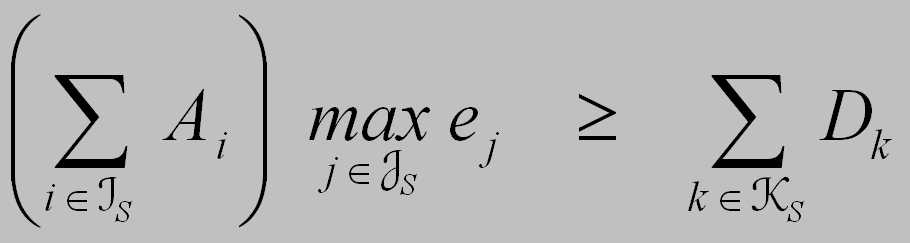
|
(5) |
where Ai denotes the ability (the energy) of the i-th participant, ej denotes the efficiency of the j-th solution, Dk denotes the difficulty (the energy) of the k-th problem and IS, JS, KS denote the set of participants, solutions and problems on square S, respectively. According to (5), if several participants and several problems are on the square, all of them are involved in decision making. If several opportunities are on the square, one of them is chosen at random to be involved in decision-making. If several solutions are on the square, only the most efficient one is involved in decision making.
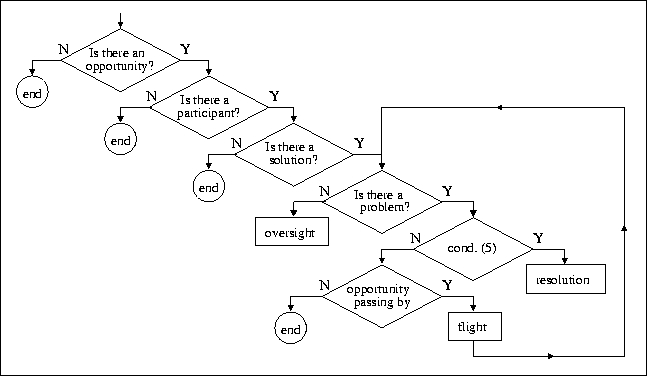
|
| Figure 9. The flow chart at a particular square. The program goes through the five rhombi along the diagonal during one single step. The sixth rhombus at the bottom requires one step by itself. If the loop on the right is entered, the two last rhombi on the diagonal require one simulation step |
|
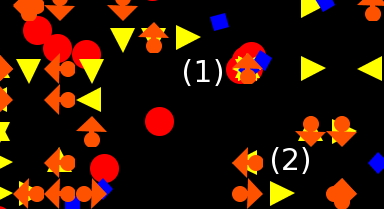
| Figure 10. A snapshot of the simulation screen. Blue squares are participants, orange arrows are opportunities, red circles are solutions and yellow triangles are problems |

|
| Figure 11. The monitors of the main indicators of the model, grouped by the agents on which they are based |
|
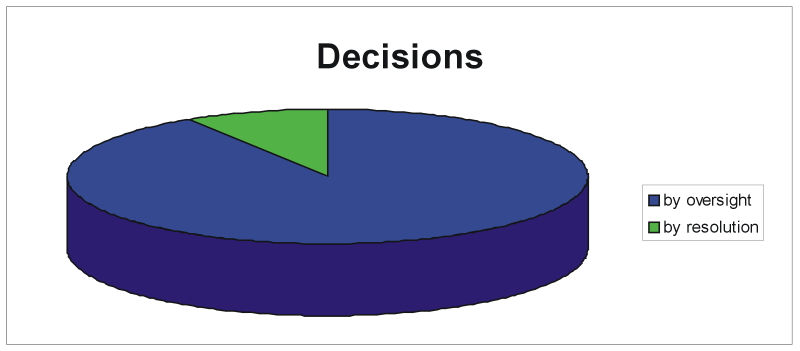
| Figure 12. The proportion of decisions by oversight and by resolution with respect to total decisions, with all parameters at base values. Outcomes have been averaged over 100 runs |
|
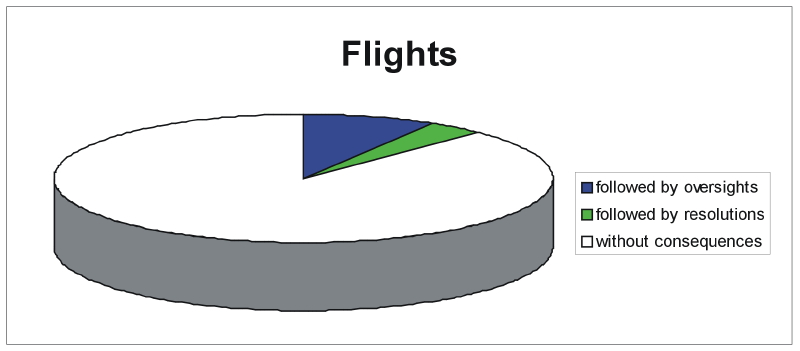
| Figure 13. The proportion of flights followed by decisions by oversights, flights followed by decisions by resolution and flights without immediate consequences when all parameters are at base values. Outcomes have been averaged over 100 runs |
|
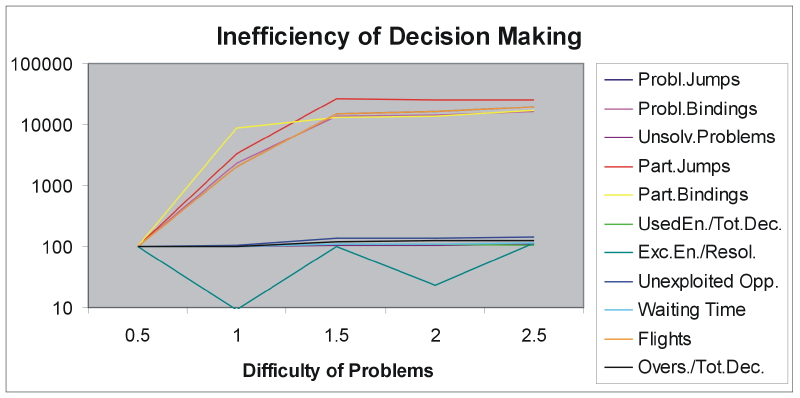
| Figure 14. The indicators proposed by Cohen, March and Olsen (1972) to represent the inefficiency of decision making, plotted as functions of the difficulty of problems. Logarithmic scale of percent values. Original values have been averaged over 100 runs |
|
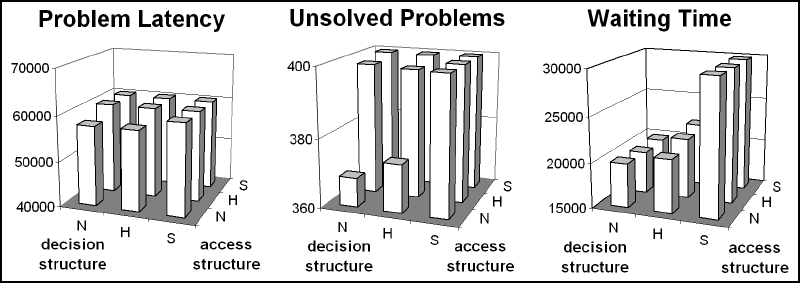
| Figure 15. Problem latency, number of unsolved problems and waiting time when problem difficulty is at 0.5. The labels N, H and S denote the non-segmented, hierarchical and specialized structure, respectively. All other parameters at base values. Outcomes have been averaged over 100 runs |
|
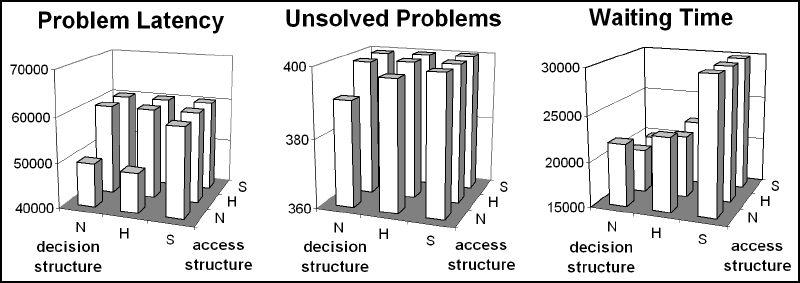
| Figure 16. Problem latency, number of unsolved problems and waiting time when problem difficulty is at 1.5. The labels N, H and S denote the non-segmented, hierarchical and specialized structure, respectively. All other parameters at base values. Outcomes have been averaged over 100 runs |
|
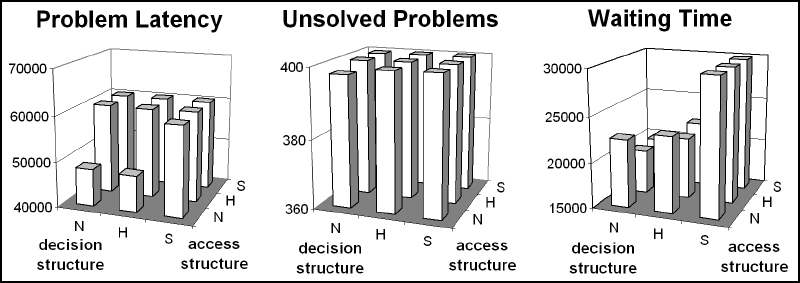
| Figure 17. Problem latency, number of unsolved problems and waiting time when problem difficulty is at 2.5. The labels N, H and S denote the non-segmented, hierarchical and specialized structure, respectively. All other parameters at base values. Outcomes have been averaged over 100 runs |
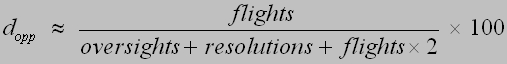
|
(6) |
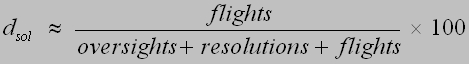
|
(7) |
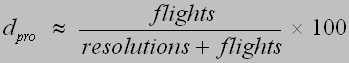
|
(8) |
|
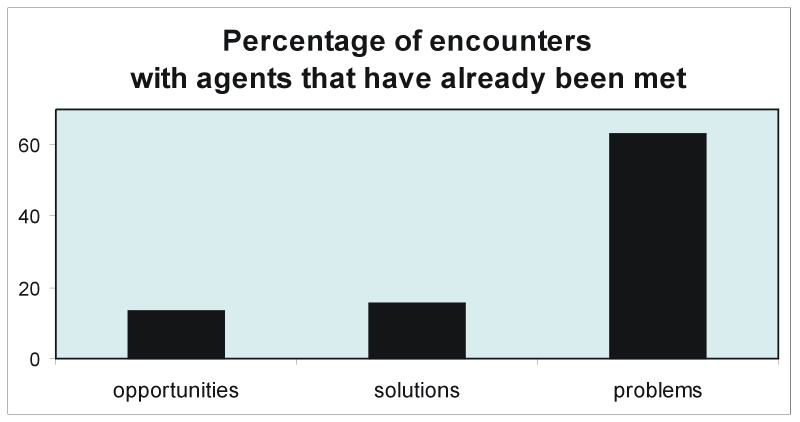
| Figure 18. Percentage of the total number of encounters with opportunities, solutions and problems, that occur with opportunities, solutions and problems that have already been met. In order to measure these quantities it has been stipulated that opportunities, solutions and problems exit the organization once a decision is made, and that no other in- or out-flows take place. All other parameters are at base values. Outcomes have been averaged over 100 runs |

|
| Figure 19. The percentage of decisions by resolution on the most important opportunities (white bars) and the least important opportunities (black bars), for various combinations of non-segmented (N) and hierarchical (H) structures. Outcomes have been averaged over 100 runs |
AXELROD R. and Tesfatsion L. (2006), "A Guide for Newcomers to Agent-Based Modeling in the Social Sciences", in L. Tesfatsion and K.L. Judd (eds.) Handbook of Computational Economics, Vol. 2: Agent-Based Computational Economics (Appendix A), Elsevier North-Holland, Amsterdam.
BAUM J.A.C. (1999), "Whole-Part Coevolutionary Competition in Organizations", in J.A.C. Baum and B. McKelvey (eds.) Variations in Organization Science: In Honor of Donald T. Campbell, Sage Publications, Thousand Oaks.
BENDOR J., Moe T.M. and Shotts K.W. (2001), "Recycling the Garbage Can: An Assessment of the Research Program", American Political Science Review, 95, 169-190.
BURTON R.M. and Obel B. (1995), "The Validity of Computational Models in Organization Science: From model realism to purpose of the model", Computational and Mathematical Organization Theory, 1: 57-72.
CARLEY K.M. (1986a), "Measuring Efficiency in a Garbage Can Hierarchy", in J.G. March and R. Weissinger-Baylon (eds.), Ambiguity and Command: Organizational Perspectives on Military Decision-Making, Pitman Publishing Inc., Marshfield.
CARLEY K.M. (1986b), "Efficiency in a Garbage Can: Implications for crisis management", in J.G. March and R. Weissinger-Baylon (eds.), Ambiguity and Command: Organizational Perspectives on Military Decision-Making, Pitman Publishing Inc., Marshfield.
CHERRY B. (2000), "The Irony of Telecommunications Deregulation: Assessing the Role Reversal in U.S. and EU Policy", in I. Vogelsang and B.M. Compaine (eds.), The Internet Upheaval: Raising Questions, Seeking Answers in Communication Policy, The MIT Press, Cambridge (MA).
COHEN M.D. and March J.G. (1974), Leadership and Ambiguity: The American college president, McGraw-Hill, New York.
COHEN M.D., March J.G. and Olsen J.P. (1972), "A Garbage Can Model of Organizational Choice", Administrative Science Quarterly, 17, 1-25. Reprinted (1986) in J.G. March and R. Weissinger-Baylon (eds.), Ambiguity and Command: Organizational Perspectives on Military Decision-Making, Pitman Publishing Inc., Marshfield. Reprinted (1988) in J.G. March (ed.), Decisions and Organizations, Basil Blackwell, Oxford.
COHEN M.D. and Sproull L.S., eds. (1996), Organizational Learning, Sage Publications, Thousand Oaks.
CYERT R.M. and March J.G. (1963), A Behavioural Theory of the Firm, Prentice-Hall, Englewood Cliffs.
DAFT R. (1982), "Bureaucratic vs non bureaucratic structures and the process of innovation and change", Researh in the Sociology of Organizations, 1, 129-166.
DI MAGGIO P.J. and Powell W.W. (1983), "The Iron Cage Revisited: Institutional isomorphism and collective rationality in organizational fields", American Sociological Review, 48, 147-160. Reprinted (1991) in W.W. Powell and P.J. DiMaggio (eds.), The New Institutionalism in Organizational Analysis, The University of Chicago Press, Chicago.
FIORETTI G. and Lomi A. (2008), "The garbage Can Model of Organizational Choice: An Agent-Based Reconstruction", Simulation Modelling Practice and Theory, forthcoming.
GAVETTI G. and Levinthal D. (2000), "Looking forward and looking backward: Cognitive and experiential search", Administrative Science Quarterly, 45, 113.
GIBBONS R. (2003), "Team Theory, Garbage Cans and Real Organizations: Some history and prospects of economic research on decision making in organizations", Industrial and Corporate Change, 12, 753-787.
GREVE H. (2003), Organization Learning From Performance Feedback. A Behavioural Perspective on Innovation and Change, Cambridge University Press, Cambridge.
HSU G. and Hannan M.T. (2005), "Identities, genres, and organizational forms", Organization Science, 16, 474 - 490.
KINGDON J.W. (1984), Agendas, Alternatives, and Public Policies, Little, Brown and Company, Boston.
LAI S.K. (1998), "From Organized Anarchy to Controlled Structure: Effects of Planning on the Garbage-Can Decision Processes", Environment and Planning B: Planning and Design, 25, 103-126.
LAI S.K. (2003), "Effects of Planning on the Garbage-Can Decision Processes: A Reformulation and Extension", Environment and Planning B: Planning and Design, 30, 379-389.
LANE D.A. and Maxfield R.R. (2005), "Ontological Uncertainty and Innovation", Journal of Evolutionary Economics, 15, 3-50.
LEACH S. (1997), "The Local Government Review: A 'Policy Process' Perspective", Local Government Studies, 23, 18-38.
LEVITT B. and Nass C. (1989), "The Lid on the Garbage Can: Institutional Constraints on Decision Making in the Technical Core of College-Text Publishers", Administrative Science Quarterly, 34, 190-207.
LIPSON M. (2007), "A Garbage Can Model of UN Peacekeeping", Global Governance, 13, 79-97.
LOMI A. and Cacciaguerra S. (2003), "Organizational Decision Chemistry Part I: Representation." Paper presented at the 2003 Conference of the North American Association for Computational Social and Organizational Science (NAACSOS), Pittsburgh.
LOMI A. and Larsen E., eds. (2001), Dynamics of organizations: Computational models and organization theories, The MIT Press, Cambridge (MA) / AAAI Press, Palo Alto.
LYNN L.H. (1982), How Japan innovates: A comparison with the U.S. in the case of oxygen steelmaking, Westview Press, Boulder.
MARCH J.G. (1978), "Bounded rationality, ambiguity, and the Engineering of Choice", The Bell Journal of Economics, 9, 587-608.
MARCH, J.G. (1994), A Primer on Decision Making, The Free Press, New York.
MARCH J.G. (2001), "Foreword", in A Lomi and E. Larsen, (eds), Dynamics of organizations: Computational models and organization theories, The MIT Press, Cambridge (MA) / AAAI Press, Palo Alto.
MARCH J.G. and Olsen J.P., eds. (1976a), Ambiguity and Choice in Organizations, Universitetsforlaget, Bergen.
MARCH J.G. and Olsen J.P. (1976b), "Organizational Choice Under Ambiguity", in J.G. March and J.P. Olsen (eds.), Ambiguity and Choice in Organizations, Universitetsforlaget, Bergen.
MARCH J.G. and Olsen J.P. (1976c), "Organizational Learning and the Ambiguity of the Past", in J.G. March and J.P. Olsen (eds.), Ambiguity and Choice in Organizations, Universitetsforlaget, Bergen.
MARCH J.G. and Olsen J.P. (1989), Rediscovering Institutions: The organizational Basis of Politics, The Free Press, New York.
MARCH J.G. and Weissinger-Baylon R. (1986), eds., Ambiguity and Command: Organizational Perspectives on Military Decision-Making, Pitman Publishing Inc., Marshfield.
MARTIN J. (1981), "A Garbage Can Model of the Psychological Research Process", American Behavioural Scientist, 25, 131-151.
MASUCH M. and LaPotin P. (1989), "Beyond Garbage Cans: An AI model of organizational choice", Administrative Science Quarterly, 34, 38-67.
MEZIAS S.J. and Scarselletta M. (1994), "Resolving Financial Reporting Problems: An Institutional Analysis of the Process", Administrative Science Quarterly, 39, 654-678.
MILLER J. (2001), "Evolving Information Processing Organizations", in A. Lomi and E. Larsen (eds.), Dynamics of organizations: Computational models and organization theories, The MIT Press, Cambridge (MA) / AAAI Press, Palo Alto.
NELSON R.R. and Winter S.G. (1982), An Evolutionary Theory of Economic Change, Harvard University Press, Cambridge (MA).
OLSEN J.P. (2001), "Garbage Cans, New Institutionalism, and the Study of Politics", American Political Science Review, 95, 191-198.
PADGETT J.F. (1980), "Managing Garbage Can Hierarchies", Administrative Science Quarterly, 25, 583-602.
PETERS B.G. (1996), "Political Institutions, Old and New", in R. Goodin and H.D. Klingemann (eds.), A New Handbook of Political Science, Oxford University Press, New York.
RICHARDSON J. (2001), "Policy-making in the EU: Interests, ideas and garbage cans of primeval soup", in J. Richardson (ed.), European Union: Power and policy-making, Routledge, London.
ROMELAER P. and Huault I. (2002), "International Career Management: The Relevance of the Garbage-Can Model", CREPA working paper 80.
SCHELLING T.C. (1971), "Dynamic Models of Segregation", Journal of Mathematical Sociology, 1, 143-186.
SPENDER J.C. (1996), "Making Knowledge the Basis of a Dynamic Theory of the Firm", Strategic Management Journal, 17, 45-62.
SPENDER J.C. and Grant R.M. (1996), "Knowledge and the Firm: Overview", Strategic Management Journal, 17, 5-9.
TAKAHASHI N. (1997), "A Single Garbage Can Model and the Degree of Anarchy in Japanese Firms", Human Relations, 50, 91-108.
WARGLIEN M. and Masuch M. (1996), eds., The Logic of Organizational Disorder, Walter De Gruyter, Berlin.
WEICK K.E. (1979), The Social Psychology of Organizing, Ch. VII, Random House, New York.
WEICK K.E. (1995), Sensemaking in Organizations, Sage Publications, Thousand Oaks.
ZAHARIADIS N. (2003), Ambiguity & Choice in Public Policy, Ch. VI, Georgetown University Press, Washington.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2008]