Phillip Stroud, Sara Del Valle, Stephen Sydoriak, Jane Riese and Susan Mniszewski (2007)
Spatial Dynamics of Pandemic Influenza in a Massive Artificial Society
Journal of Artificial Societies and Social Simulation
vol. 10, no. 4 9
<https://www.jasss.org/10/4/9.html>
For information about citing this article, click here
Received: 13-Apr-2007 Accepted: 14-Jun-2007 Published: 31-Oct-2007
 Abstract
Abstract| Table 1: Selected attributes that characterize the state of each individual (i.e. the members of the EPerson class) | |||
| Attribute | Sub-attribute | Type | Description |
| fID | long | Unique identifier for each individual | |
| fDemographics | EDemographics ::fHHSize ::hHHId ::fHomeLoc ::fAge ::fGender | int long long int int | Class that holds:: Household size Unique household id household's half-block id Person's age (years) male or female |
| fPersonStatus | EPersonStatus ::CurrentlyExposed ::HasBeenInfected ::HasBeenTreated ::HasBeenContagious ::IsRecovered ::HasBeenExposed ::IsDead | bool bool bool bool bool bool bool | A person's disease-related history and status. |
| fContacts | list of long | List of all other persons contacted by this person so far | |
| fSchedule | Linked list of scheduleComponents, each having: ::location ::arrivalTime ::activityDuration ::activityType | long time time int | sequence of person's daily activities building or block id activity start time activity duration enum of 8 activity types |
| fActivityEnum | EActivities ::fFracFound ::fFracMaskUsage | list of float list of float | for each activity, the fraction of a person's contacts that would be traced, and the fraction of time the person would wear a mask |
| fGeneration | int | one plus the fGeneration of the person that infected this person. | |
| fDiseaseState | EDiseaseAttributes ::prodromal ::symptomatic ::infectiousness ::susceptibility ::incapacitation | int int float float int | indicators of whether this person is prodromal, symptomatic, or incapacitated, and their infectiousness and susceptibility levels. |
| fTreatmentSet | list of int | the set of treatments that are currently in effect for this person | |
| fDeliveredTreatmentSet | list of int | the set of treatments that have ever been delivered to this person | |
| fTreatmentInfectivityFactor | float | an infectivity reduction factor that corresponds to the treatments currently in effect for this person | |
| fCurrentRoom | long | ID of room that person currently occupies | |
| fNextDepartTime | time | time of person's next disease state change | |
| fUsingMask | bool | True if person is currently wearing a mask | |
| fFamilyMemberSickAtHome | bool | True if person has sick household members | |
|
|
|
|
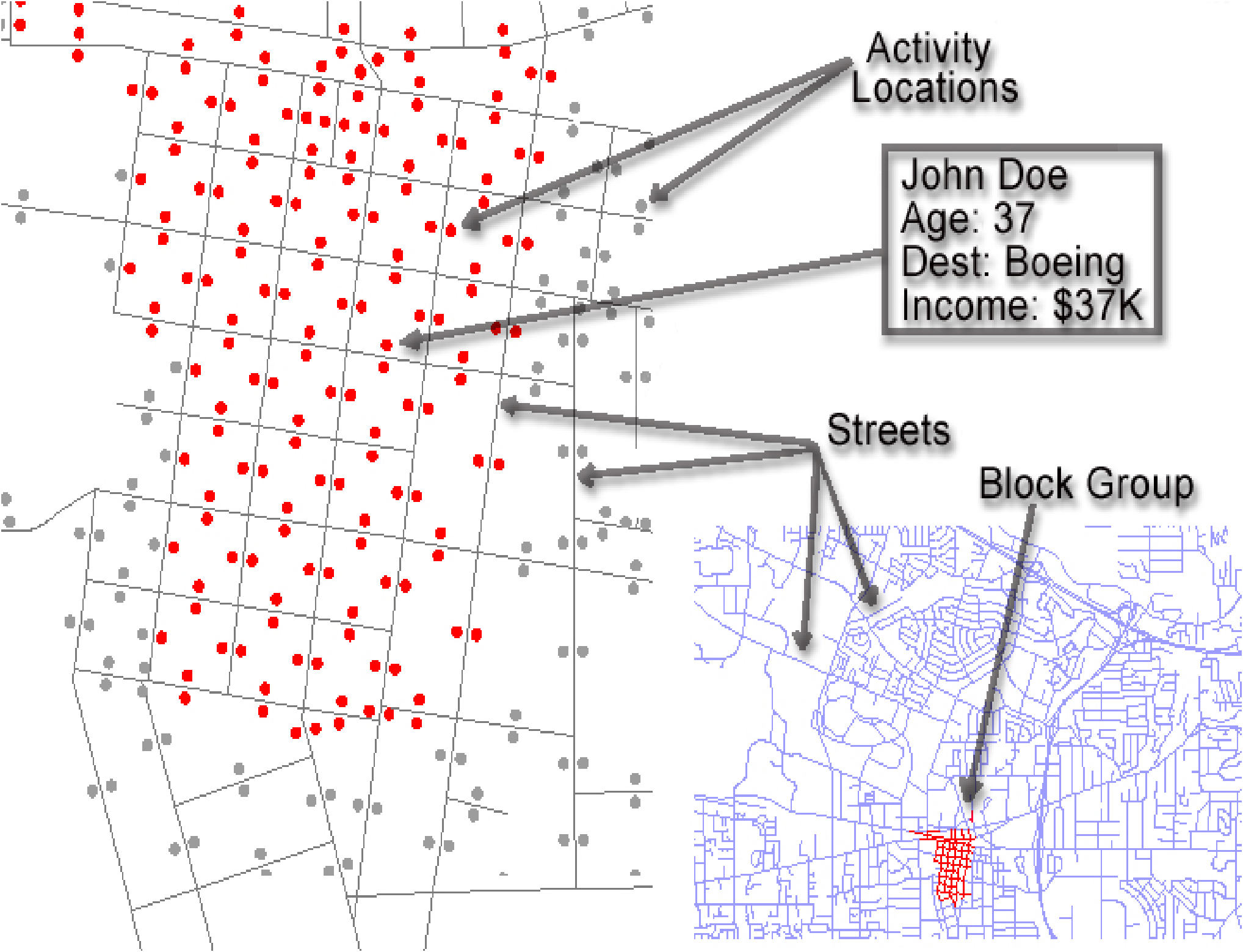
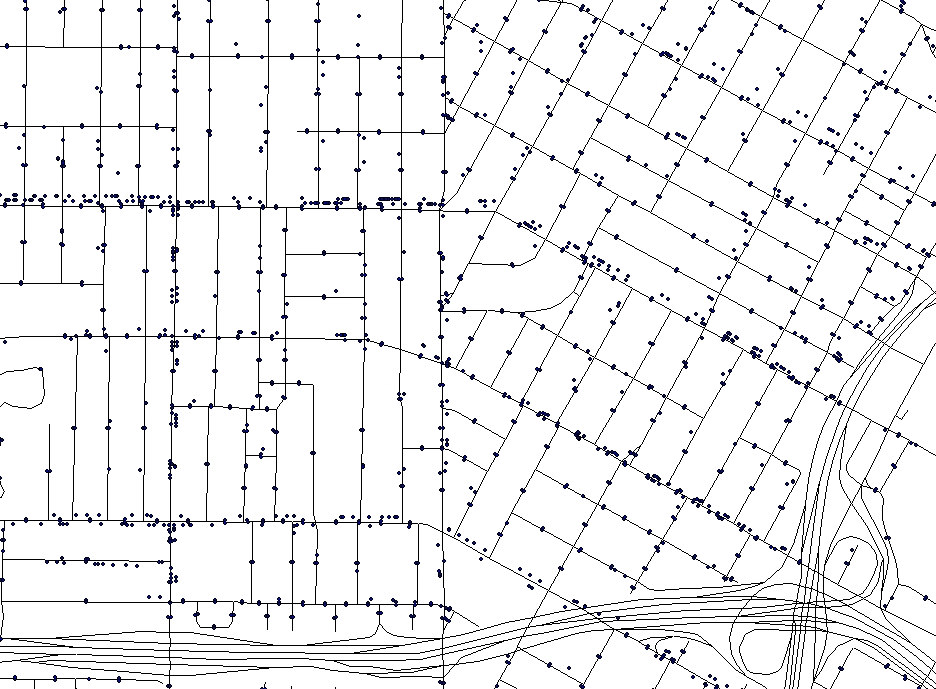
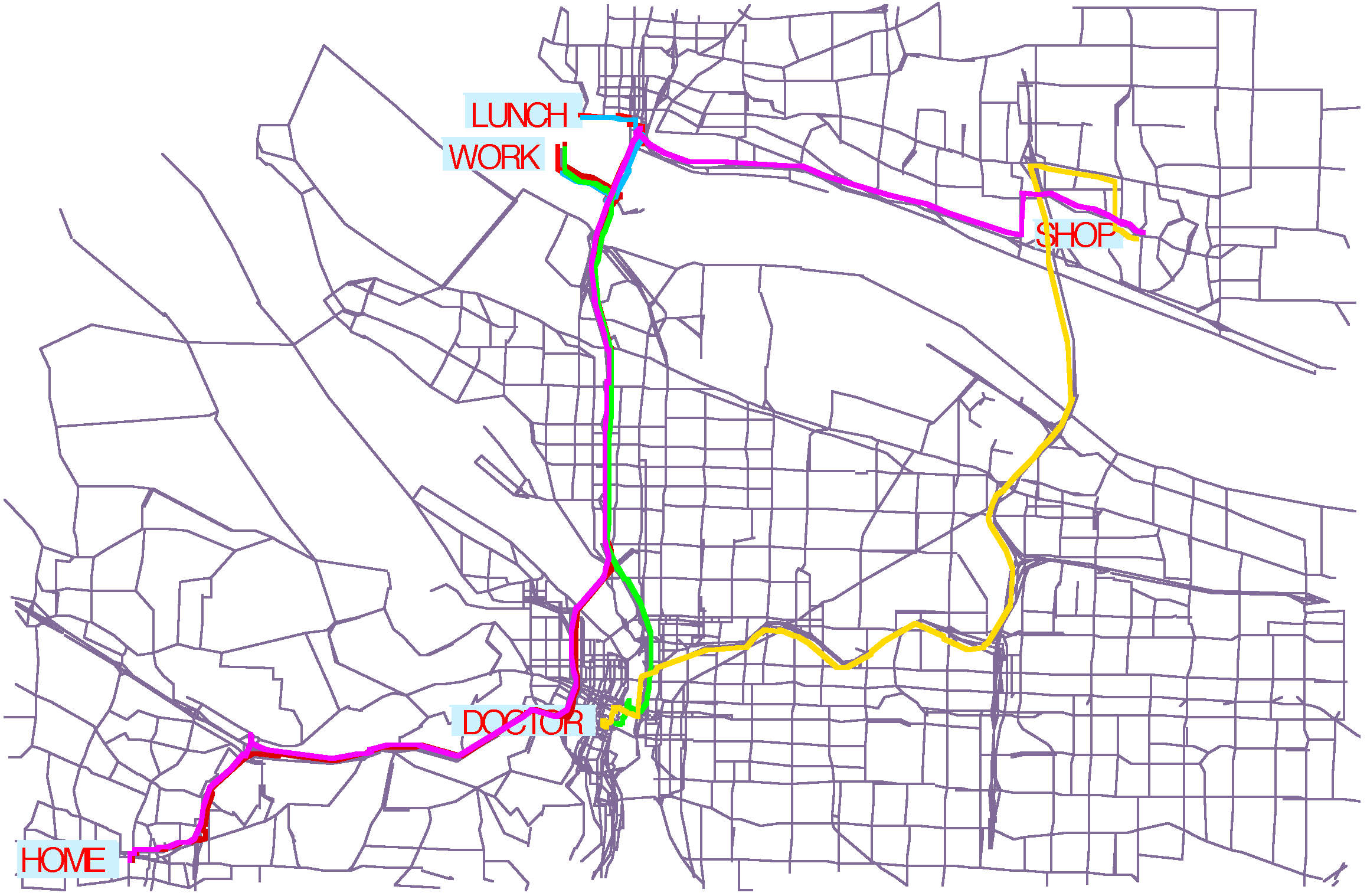
| Figure 1. Households are geo-located to city half-blocks to match relevant demographic statistics in each of 12,226 block groups (top left). Business locations are geo-located by their business address (top right). Each individual is assigned an activity schedule (bottom left). Activity patterns are drawn from actual household activity surveys (bottom right) | |
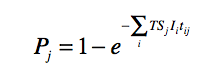
|
where tij is the time that susceptible person j was in the same sublocation as infectious person i, and the sum extends over all infectious persons that co-occupied the sublocation with individual j. EpiSimS computes the co-occupation times for all overlapping pairs of individuals as they enter and leave sublocations.
|
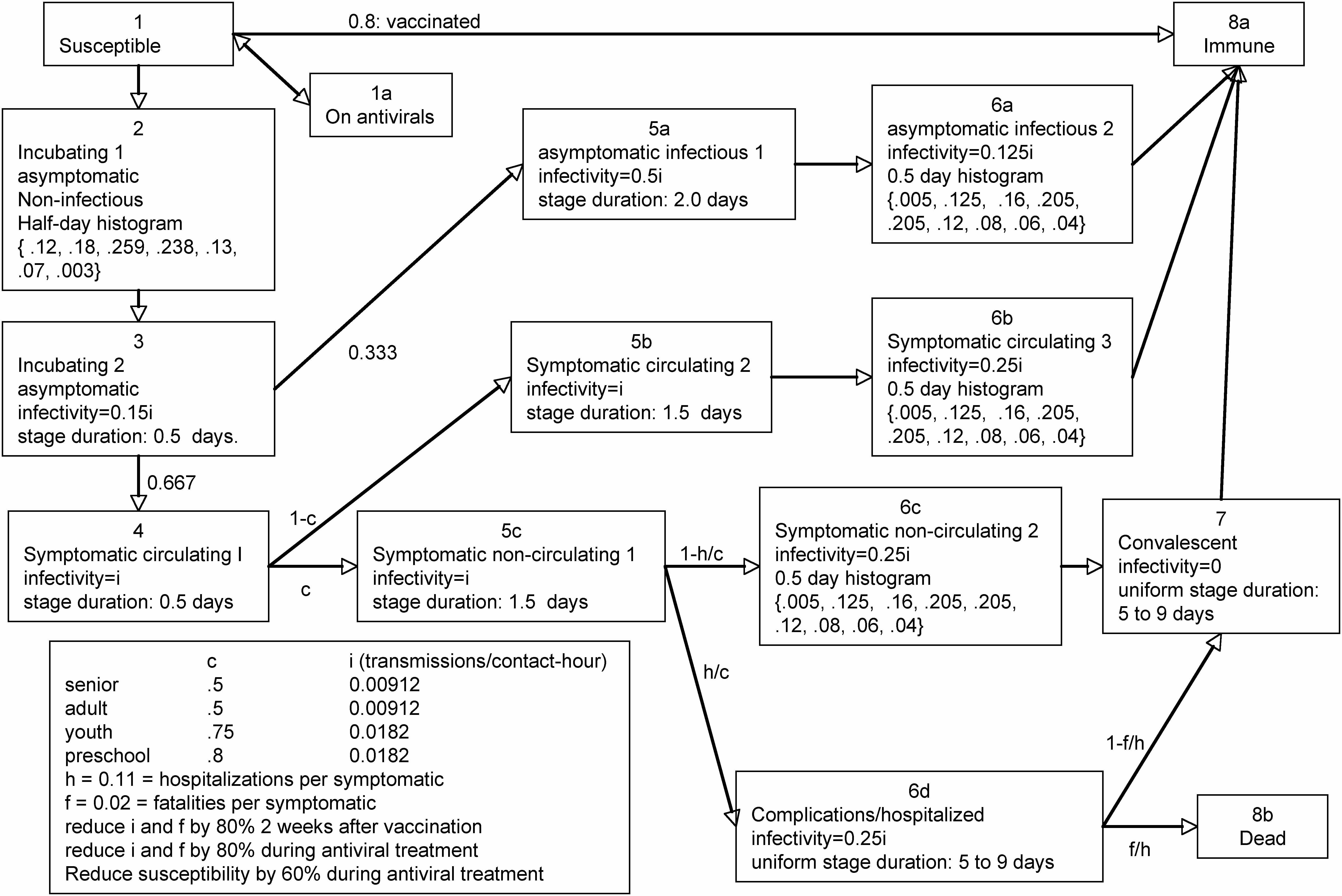
| Figure 2. The pandemic influenza disease progression model. Each individual is initially in the uninfected stage. Upon becoming infected, all untreated individuals transition to the incubating-1 stage (pre-symptomatic incubating) |
ESimulator::main
Initialize local parameters from the config file
Register to receive messages from other processors
Create and open a local event logger
Read in the disease manifestation (parameters giving fig. 2)
IF master
Read in the partition file (sublocations per location)
Read in disease states (initial health of each person)
Send each location to the appropriate processor.
Read in schedule file (activities for each person)
Send each individual to the appropriate processor.
Until endOfSimulation
receive and log results
ELSE
Receive locations
Receive individuals
Place scheduled events on event queue
Until endOfSimulation
Handle next event
101 1 52 1 1 603389 24177686 202000 24177686
This record parses as: Person 101 resides in household 1, is a 52 year old, male, worker. His household is located on city half-block 603389, which is on NAVTEQ road segment 24,177,686. His household income is $202,000. He begins the simulation at his home location.
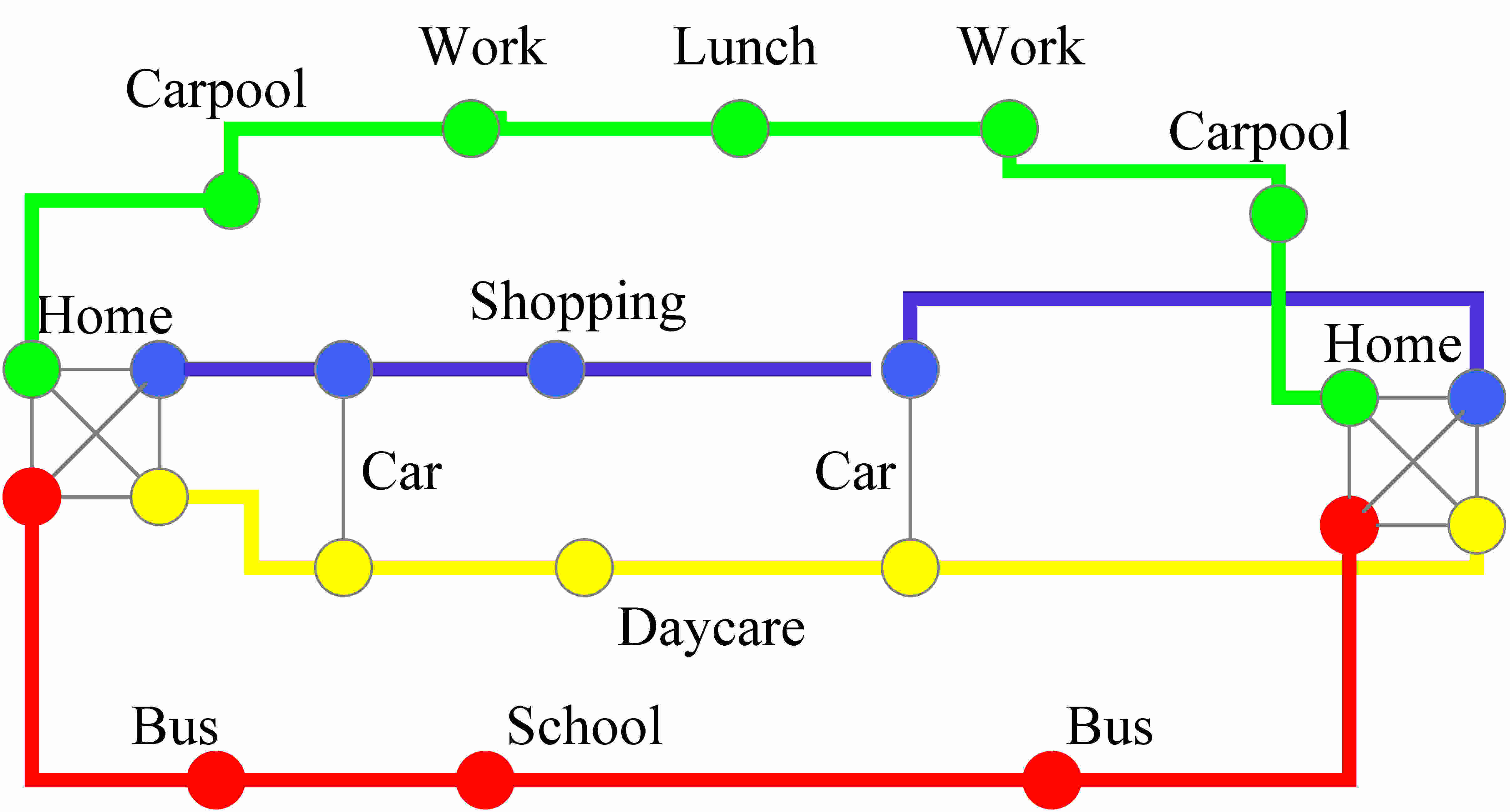
00:00:00 24177686 101 5 0 08:15:00 24177686 101 1 23914209 08:45:00 23914209 101 0 1 18:30:00 23914209 101 1 24177686 18:49:59 24177686 101 0 0 21:19:59 24177686 101 1 23937362 21:28:59 23937362 101 0 6 21:30:00 23937362 101 1 24177686 21:45:00 24177686 101 0 0The first field specifies the time (HH:MM:SS). The second field gives the road segment where the activity occurs. The third field specifies the person. Values for the 4th field specify the event type: 5-activity at start of simulation; 1- depart from activity; 0- arrive at activity. For departure events, the 5th field gives the location of the next event. For start-simulation and arrival events, the 5th field specifies the activity type: 0-home; 1-work; 2-shop; 3-visit; 4-social recreation; 5-other -an activity category allowed on the NHTS survey; 6-car pool; 7-school; 8-college.
EDiseaseTransmitter::SpreadDisease
GET list of room occupants and time since last update
Instantiate working variables
FOR each pair of room occupants
Increment their contact time
Make empty lists of infectious and susceptible people
FOR each person in list of room occupants
infectivity = GetInfectivity of person
IF (infectivity > 0) add person to list of infectiousPersons;
susceptibility = GetSusceptibility of person
IF (susceptibility > 0) add person to list of susceptiblePersons
IF (person is CurrentlyExposed) THEN
add person to list of exposedPersons
ELSE add person to list of unexposedPersons
END FOR
IF no one in room is infectious
MARK every person in room as unexposed
return
MARK every person in room as exposed
IF no one in room is susceptible THEN return
FOR each susceptible person in room
susceptibility = GetSusceptibility of susceptiblePerson
IF susceptiblePerson is wearing a mask, reduce susceptiblity
sumOfLogs = 0
FOR all infectious persons in room
infectivity = GetInfectivity of infectiousPerson
reduce infectivity if infectiousPerson is wearing mask
spreadability = susceptibility * infectivity
* seasonalVarFactor * TransmissionFactor
sumOfLogs += Math.log(1 - spreadability)
END FOR
prob=(1.-exp(deltaTMinutes * sumOfLogs))
rannum <- random uniform variate in (0,1)
if (rannum < prob) then susceptableperson becomes infected
end for
|
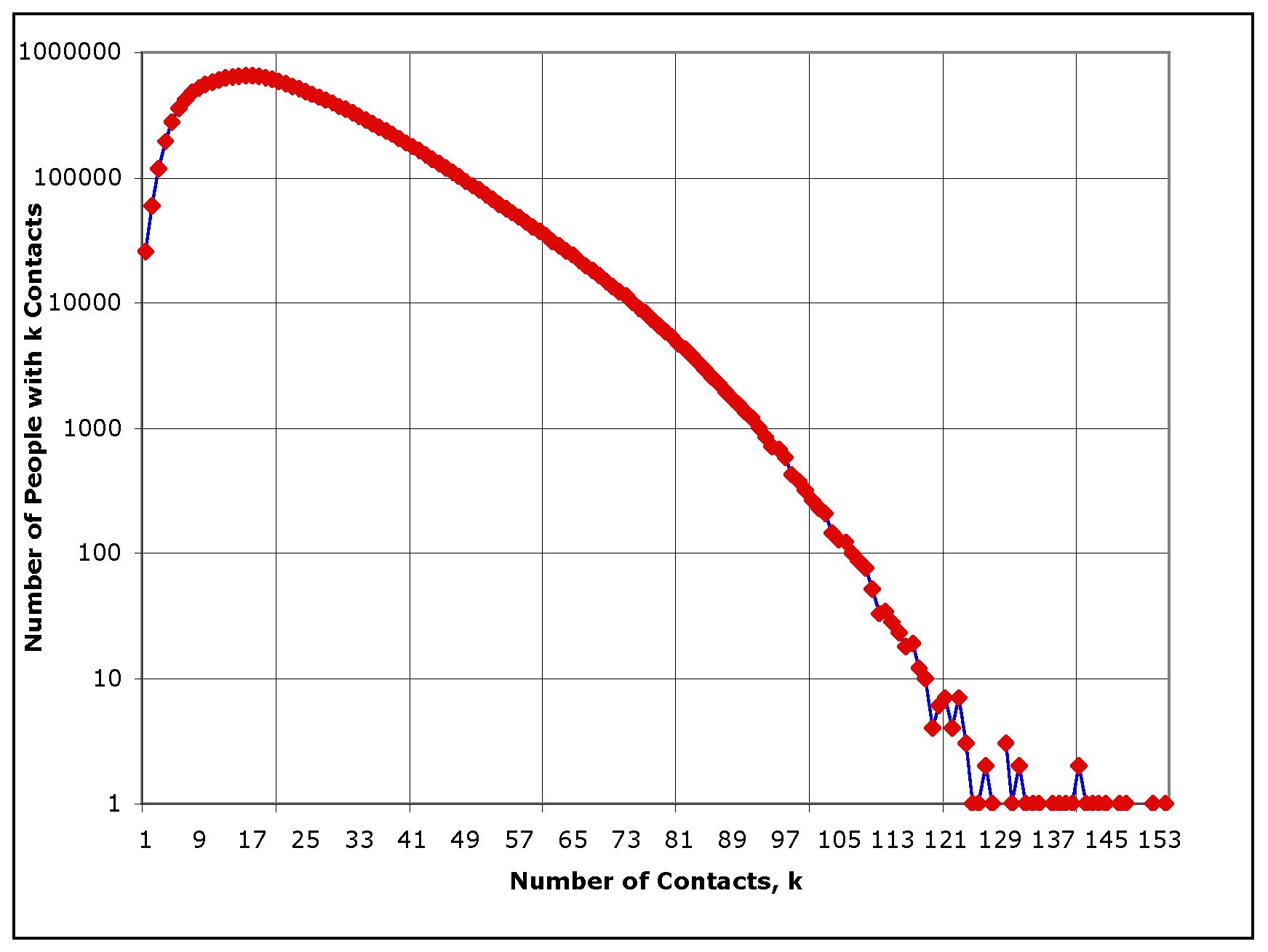
| Figure 3. The degree distribution, showing how many people have a given number of contacts per day, for the synthetic population of southern California |
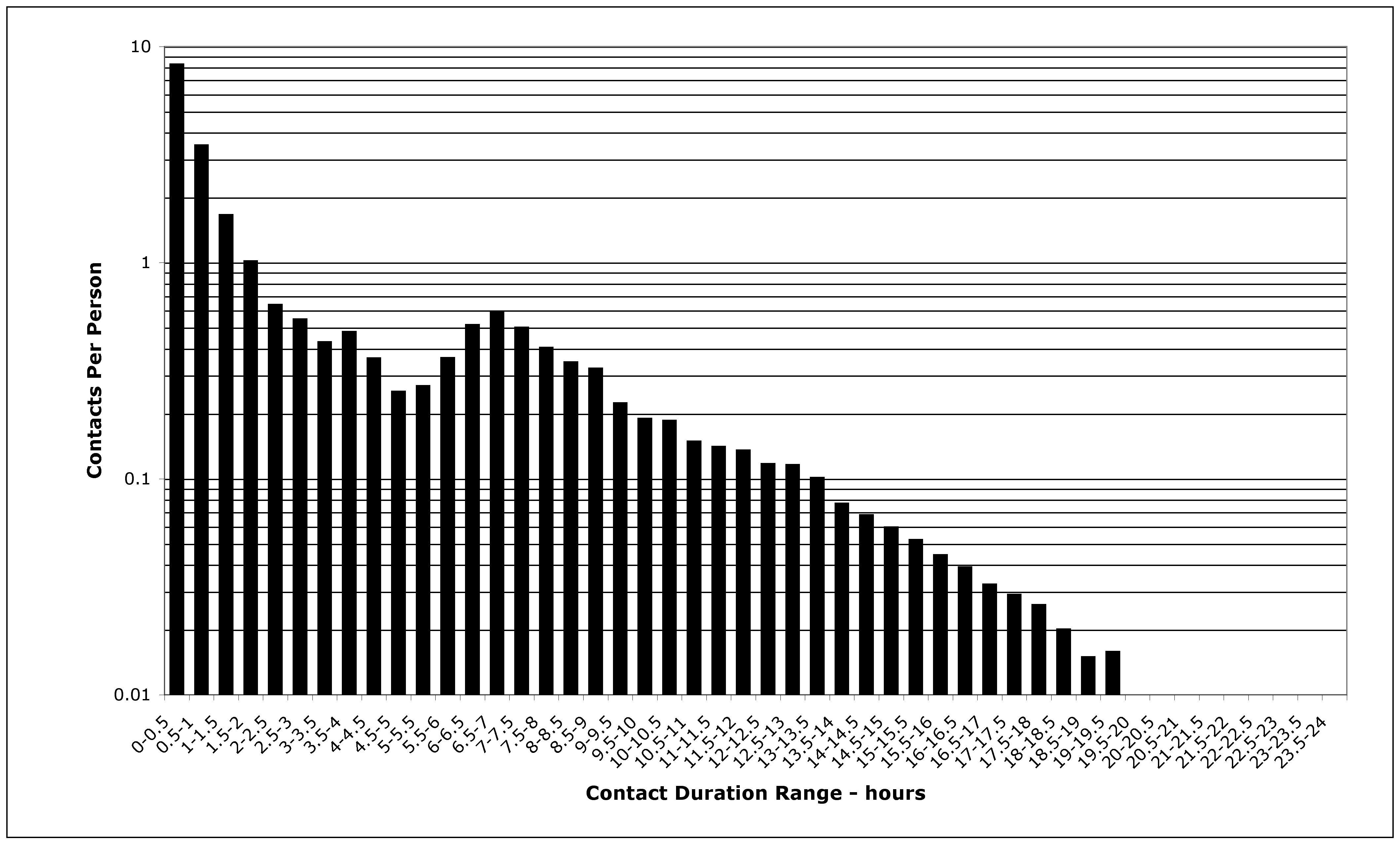
|
| Figure 4. The distribution of contact duration among people in southern California |
|
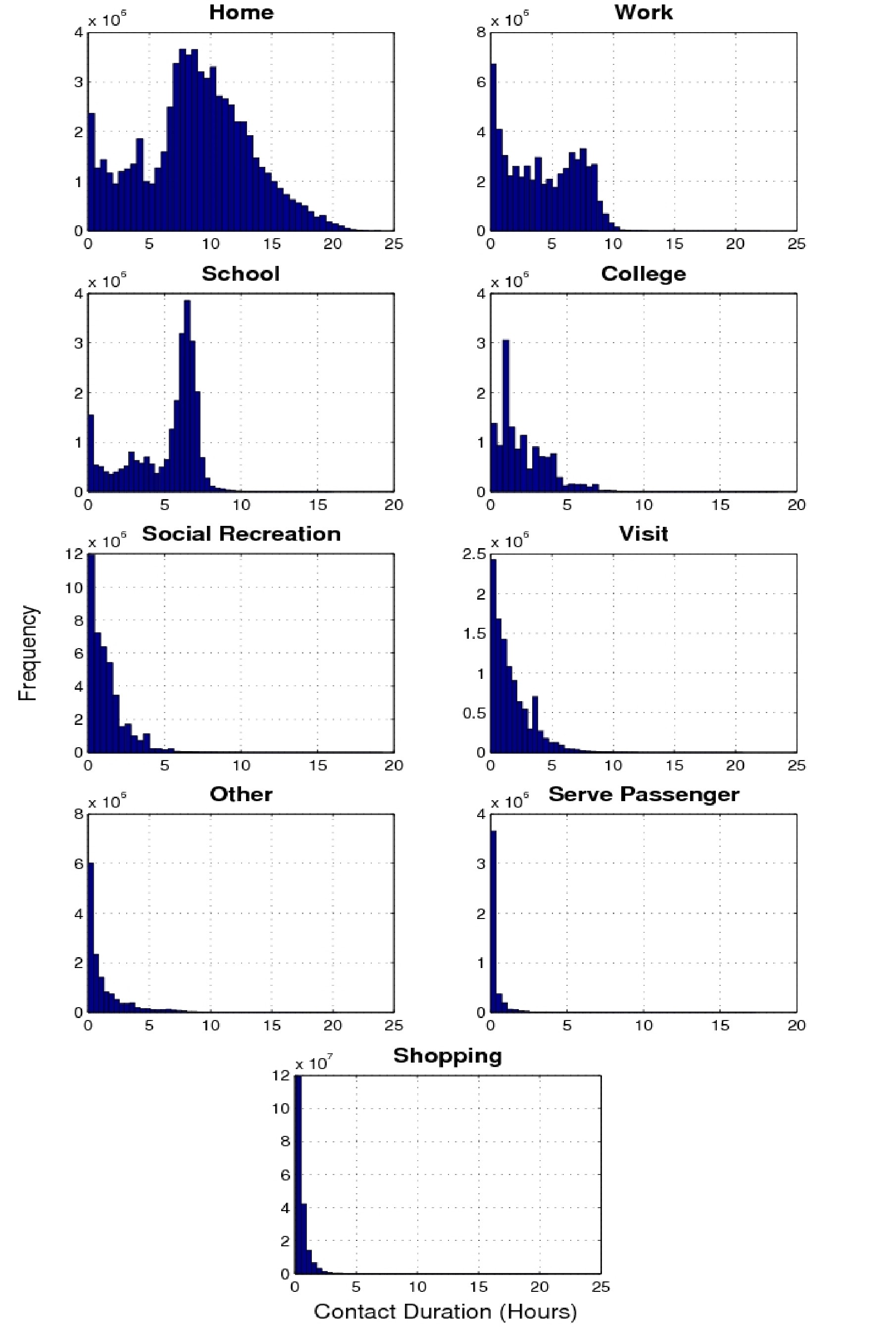
| Figure 5. The distribution of contact duration for each activity type |
| Table 2: Average duration per contact by activity category | ||
| Activity category | Average Duration | Standard Deviation |
| Home | 8 hrs 49 min | 4 hrs 28 min |
| School | 5 hrs 2 min | 2 hrs 14 min |
| Work | 4 hrs 13 min | 2 hrs 55 min |
| College | 2 hrs 6 min | 1 hr 40 min |
| Visit | 1 hr 43 min | 1 hr 39 min |
| Other | 1 hr 19 min | 1 hr 45 min |
| Social Recreation | 1 hr 12 min | 1 hr 14 min |
| Shop | 30 min | 55 min |
| Carpool | 18 min | 43 min |
|
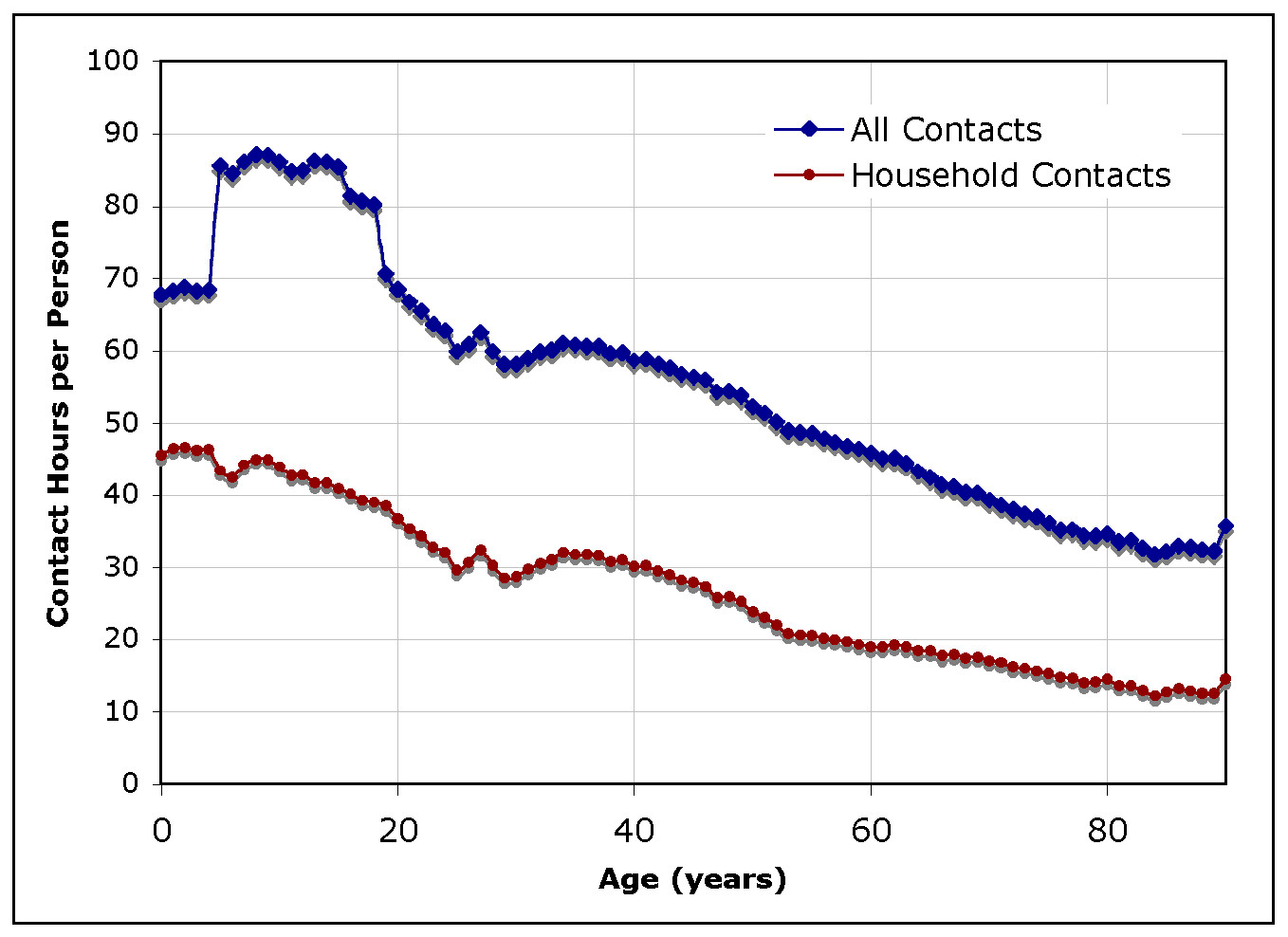
| Figure 6. Average number of total and household contacts hours per person per representative day, as a function of the age of the person |
| Table 3: Daily average number of contact hours by age group | ||||
| average contact hours per day with preschoolers | average contact hours per day with students | average contact hours per day with adults | average contact hours per day with seniors | |
| preschoolers (0-4) | 15.03 | 16.84 | 34.52 | 1.92 |
| students (5-18) | 5.84 | 46.02 | 30.86 | 1.97 |
| adults (19-65) | 4.27 | 10.89 | 36.99 | 3.56 |
| seniors (66+) | 1.61 | 4.63 | 21.62 | 7.78 |
| Table 4: Daily average number of home-related contact hours by age group | ||||
| average household contact hours per day with preschoolers | average household contact hours per day with students | average household contact hours per day with adults | average household contact hours per day with seniors | |
| preschoolers (0-4) | 7.21 | 12.45 | 25.68 | 0.69 |
| students (5-18) | 4.30 | 14.44 | 22.35 | 0.83 |
| adults (19-65) | 3.11 | 7.80 | 15.02 | 1.23 |
| seniors (66+) | 0.57 | 1.96 | 6.75 | 5.62 |
|
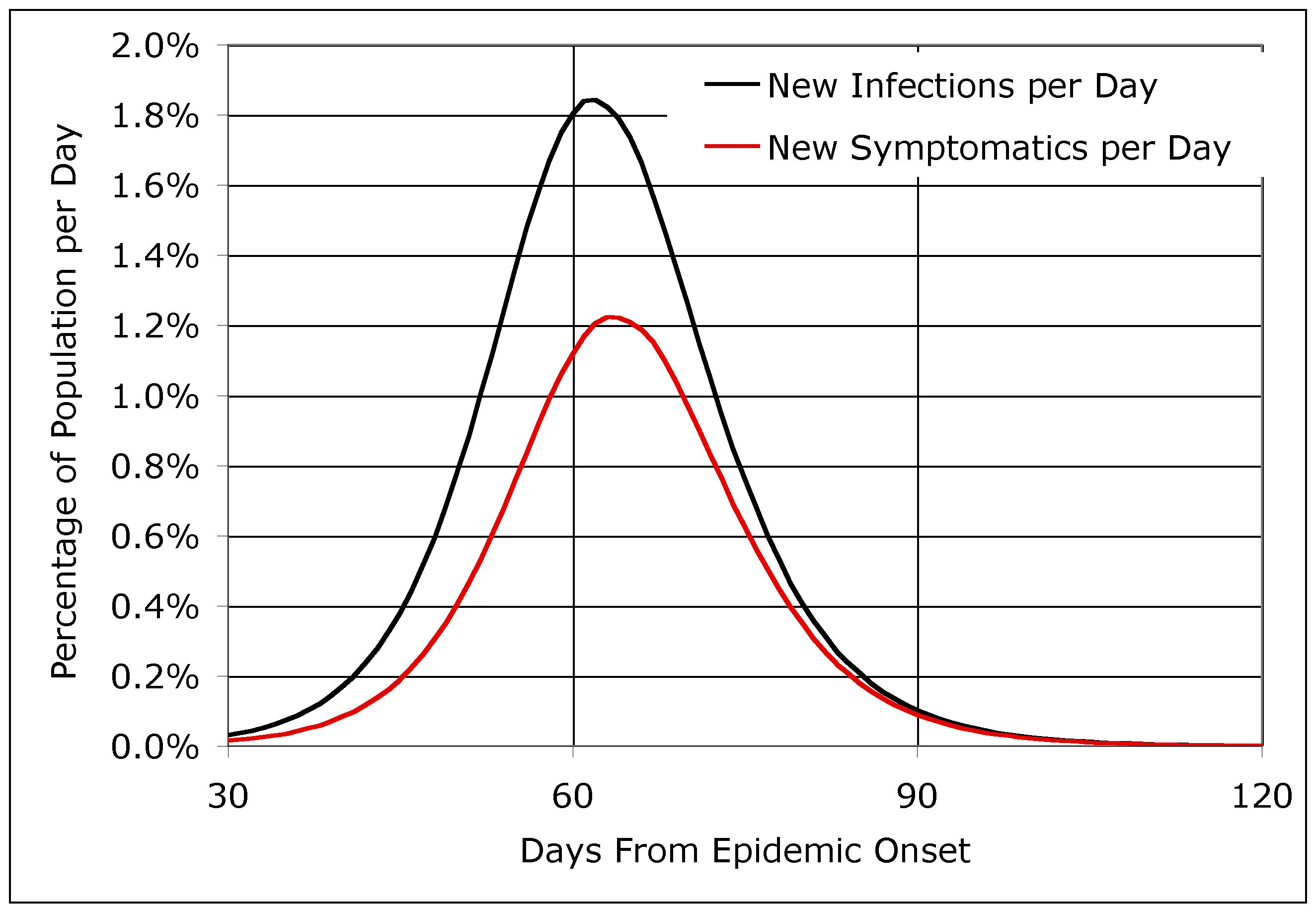
| Figure 7. The base case EpiSimS simulation run, showing the percentage of the population that becomes infected or symptomatic per day |
| Table 5: Breakout of infections by activity category | |
| Activity category | Fraction of cumulative infections |
| Home | 58.4% |
| School | 13.3% |
| Work | 13.0% |
| Shopping | 5.5% |
| Social Recreation | 3.6% |
| Visit | 3.0% |
| College | 1.8% |
| Other | 1.3% |
| Carpool | 0.1% |
|
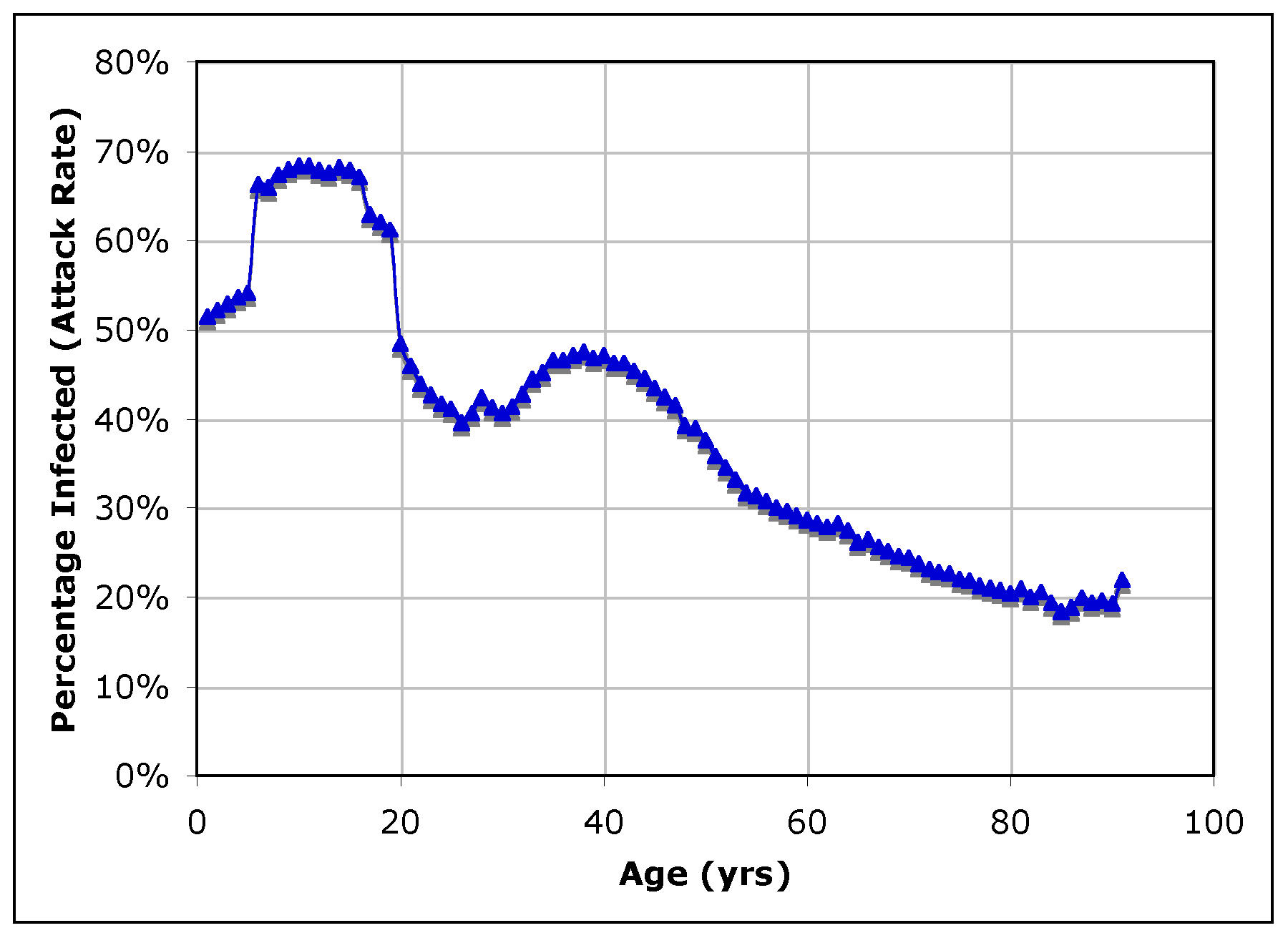
| Figure 8. Total attack rate (symptomatic and subclinical) by age cohort |
|
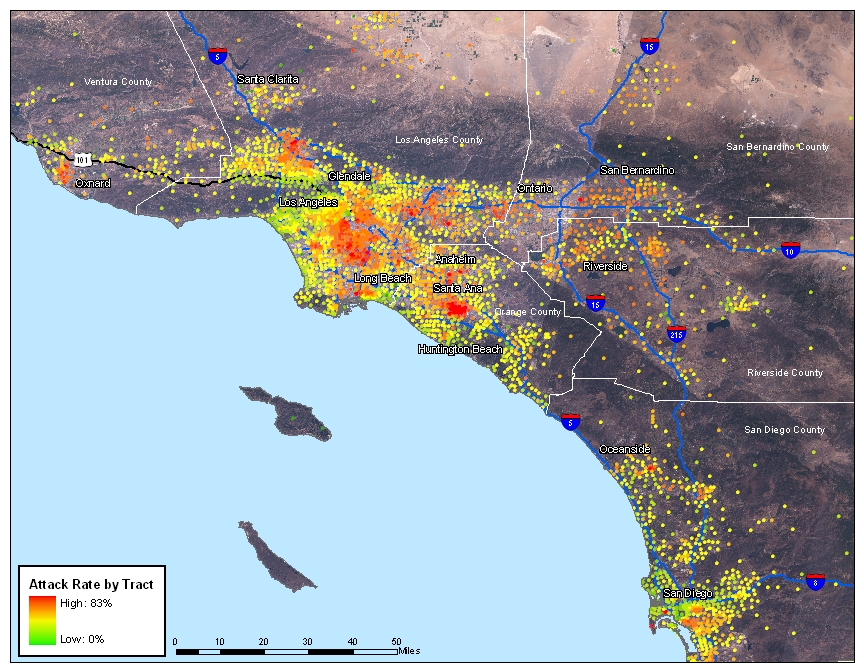
| Figure 9. Clinical attack rate by census tract, ranging from mild (green) to severe (red) |
|
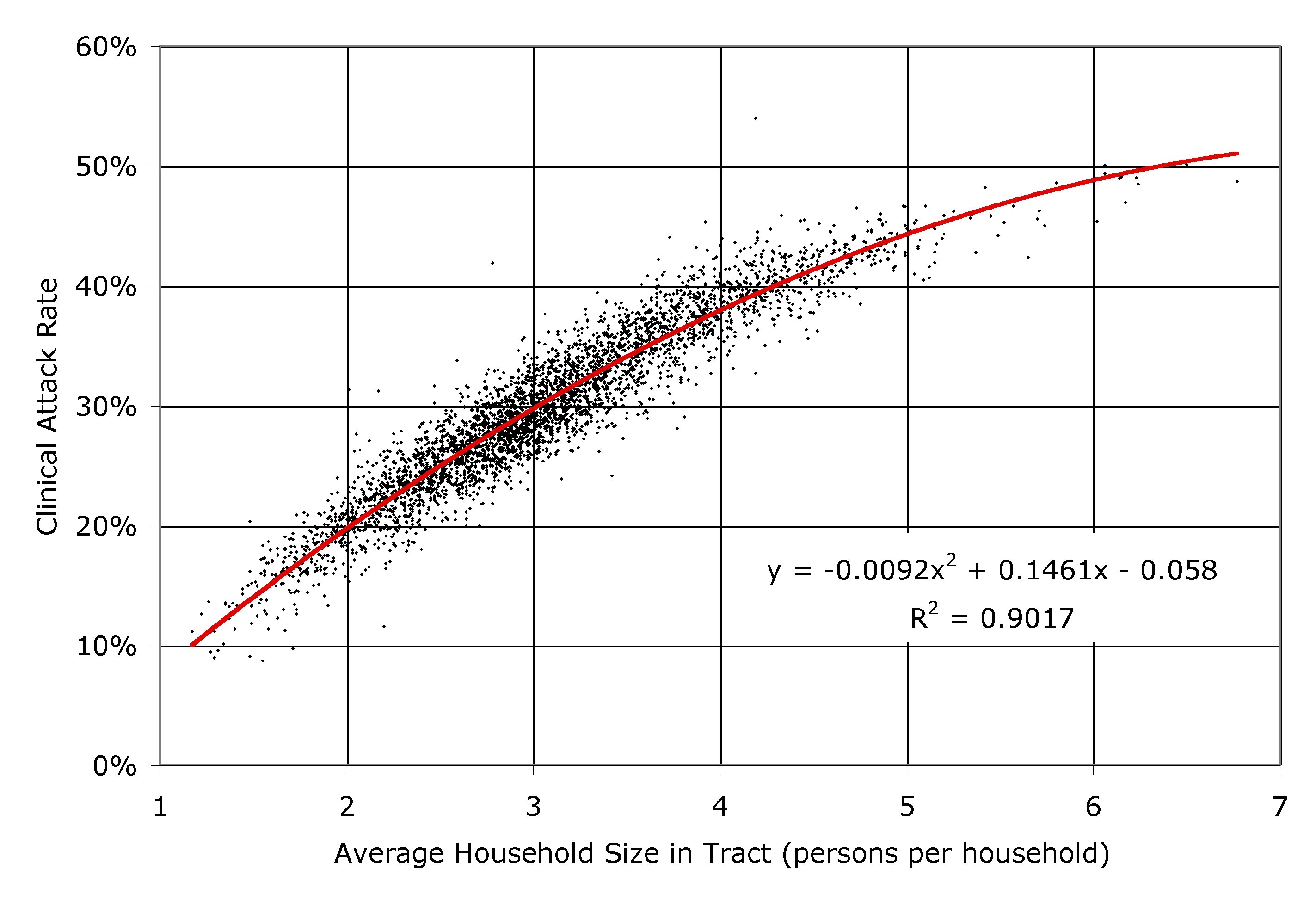
| Figure 10. The clinical attack rate plotted against the average household size (i.e. the residential population divided by the number of households) for each of the 3978 census tracts in southern California, as simulated by EpiSimS |
|
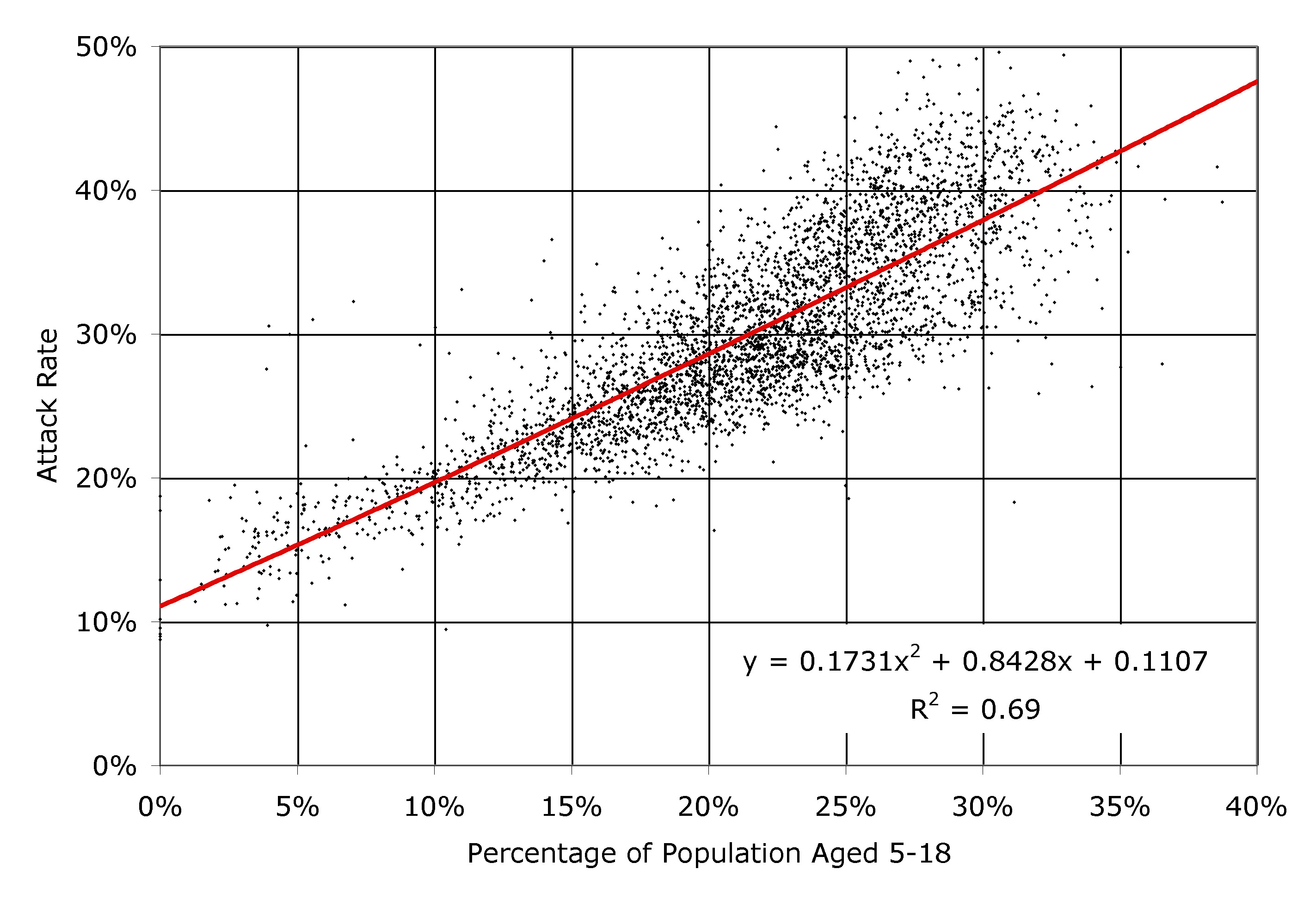
| Figure 11. The clinical attack rate plotted against the ratio of students to non-students, for each of the 3978 census tracts in southern California, as simulated by EpiSimS |
|
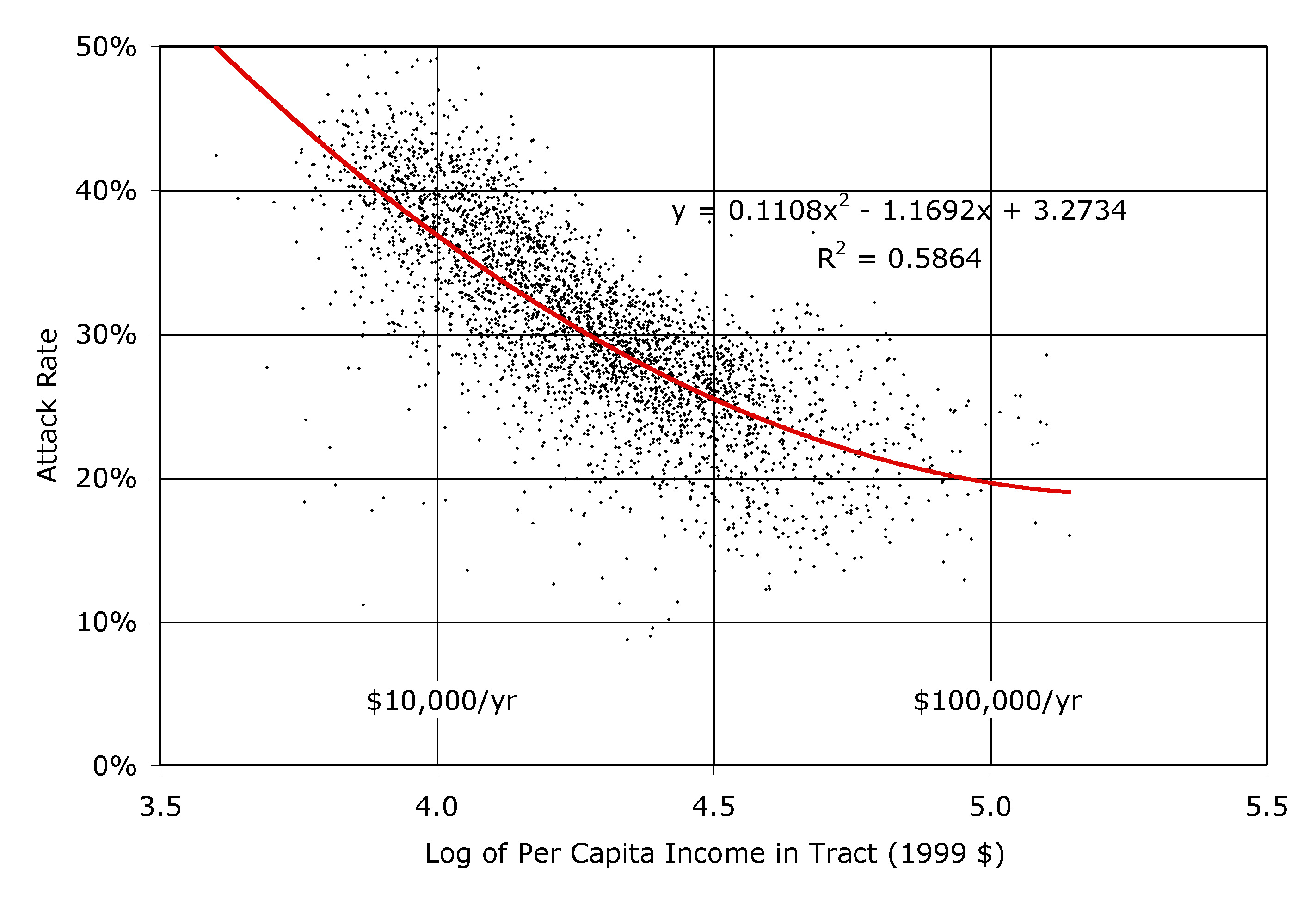
| Figure 12. The clinical attack rate plotted against the logarithm of the per capita income, for each of the 3978 census tracts in southern California, as simulated by EpiSimS |
|
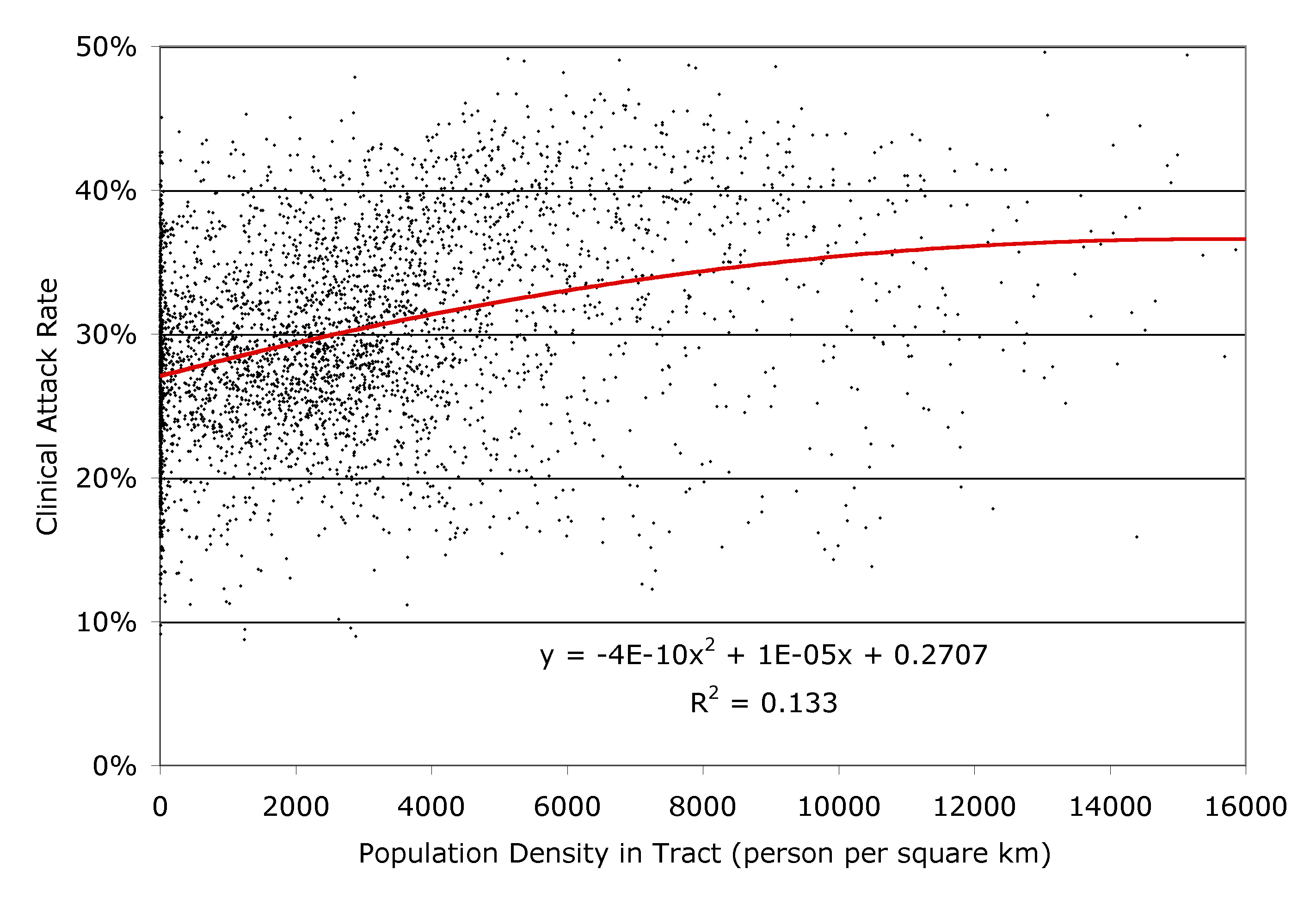
| Figure 13. The clinical attack rate plotted against the population density, for each of the 3978 census tracts in southern California, as simulated by EpiSimS |
BECKMAN R J, Baggerly K A, and McKay M D (1995) Creating Synthetic Baseline Populations, Transportation Research A 30A(64). pp. 415-429.
DUNHAM J B (2005) An Agent-based Spatially Explicit Epidemiological Model in MASON, Journal of Artificial Societies and Social Simulation 9(1)3, https://www.jasss.org/9/1/3.html.
EIDELSON B, Lustik I (2004) 'VIR-POX: An Agent-based Analysis of Smallpox Preparedness and Response Policy', Journal of Artificial Societies and Social Simulation, 7(3)6. https://www.jasss.org/7/3/6.html
EUBANK S, Goclu H, Kumar A, Marathe M, Srinivasan A, Totoczkal Z, Wang N (2004) Modelling disease outbreaks in realistic urban social networks, Nature 429, 13 May 2004. pp. 180-184.
FHWA (FEDERAL HIGHWAY ADMINISTRATION) (1978) Quick-response Urban Travel Estimation Techniques and Transferable Parameters, NCHRP Report 187. available from http://nationalacademies.org/trb/bookstore
FERGUSON N M, Cummings D A T, Fraser C, Cajka J C, Cooley P C, Burke D S (2006) Strategies for mitigating an influenza pandemic, Nature 442(7101), July 27, 2006. pp. 448-452.
GERMANN T C, Kadau K, Longini I M, Macken C M (2006) Mitigation strategies for pandemic influenza in the United States, Proc. Natl. Acad. Sci. U.S.A. 103, pp. 5935-5940.
GLASS R J, Glass L M, Beyeler W E, Min H J (2006) Targeted Social Distancing Design for Pandemic Influenza, Emerging Infectious Diseases 12, Nov 2006.
HALLORAN M E, Longini I M, Nizam A, Yang Y (2002) Containing Bioterrorist Smallpox, Science 298, 15 November 2002. pp. 1428-1432.
HSC (HOMELAND SECURITY COUNCIL) (2006) National Strategy for Pandemic Influenza - Implementation Plan, http://www.whitehouse.gov/homeland/nspi_implementation_briefing.pdf.
HUANG C-Y, Sun C-T, Hsieh J-L, and Lin H (2004) Simulating SARS: Small-World Epidemiological Modeling and Public Health Policy Assessments, Journal of Artificial Societies and Social Simulation 7(4)2, https://www.jasss.org/7/4/2.html.
KRETZSCHMAR M, van den Hof S, Wallinga J, van Wijngaarden J (2004) Ring vaccination and smallpox control, Emerging Infectious Diseases 10. pp. 832-841.
LONGINI I M, Halloran M E, Nizam A, Yang Y (2004) Containing Pandemic Influenza with Antiviral Agents, Am. J. of Epidemiology, 159(7) April 1, 2004, pp. 623-633.
MARTIN W A, McGuckin N A (1998) Travel estimation techniques for urban planning, NCHRP Report 365. available from http://nationalacademies.org/trb/bookstore
MICHAELS J (2003) Commercial Buildings Energy Consumption Survey, http://www.eia.doe.gov/emeu/cbecs/cbecs2003/detailed_tables_2003/detailed_tables_2003.html
NAVTEQ (2004) US Road Network Data, obtained in 2004, http://www.navteq.com
NCES (NATIONAL CENTER FOR EDUCATION STATISTICS) (2006) Common Core of Data public school data 2004-2005 school year, and Private School Universe Survey data for the 2003-2004 school year, http://nces.ed.gov/datatools/.
SIMONSEN L, Clarke M J, Schonberger L B, Arden N H, Cox N J, Fukuda K (1998) Pandemic versus Epidemic Influenza Mortality: A Pattern of Changing Age Distribution, J. Infectious Diseases 178. pp. 53-60.
SMITH L, Beckman R, Anson D, Nagel K, Williams M (1995) TRANSIMS: Transportation analysis and simulation system, Compendium of Papers of 5th Nat'l Conf on Transportation Planning Methods Applications-Volume II, Transportation Research Board, Seattle, Washington, April 1995.
STROUD P D, Sydoriak S J, Riese J M, Smith J P, Mniszewski S M, Romero P R (2006) Semi-empirical Power-law Scaling of New Infection Rate to Model Epidemic Dynamics with Inhomogeneous Mixing, Mathematical Bioscicences 203, pp. 301-318.
USCB (UNITED STATES CENSUS BUREAU) (2000) 2000 Decennial Census, database server at http://factfinder.census.gov.
USDHHS (UNITED STATES DEPARTMENT OF HEALTH AND HUMAN SERVICES) (2005) HHS Pandemic Influenza Plan, html://www.hhs.gov/pandemicflu/plan/pdf/HHSPandemicInfluenzaPlan.pdf.
USDOT (UNITED STATES DEPARTMENT OF TRANSPORTATION) (2003) NHTS 2001 Highlights Report BTS03-05, Washington, DC., http://www.bts.gov/publications/highlights_of_the_2001_national_household_travel_survey/html/executive_summary.html.
USINS (UNITED STATES IMMIGRATION AND NATURALIZATION SERVICE) (2003) Estimates of the Unauthorized Immigrant Population Residing in the United States: 1990 to 2000, http://www.dhs.gov/xlibrary/assets/statistics/publications/Ill_Report_1211.pdf.
VIBOUD C, Bjornstad O N, Smith D L, Simonsen L, Miller M A, Grenfell BT (2006) Synchrony, Waves, and Spatial Heirarchies in the Spread of Influenza. Science 312, pp. 447-451.
VOORHEES A M (1956) A general theory of traffic movement. 1955 Proceedings, Institute of Traffic Engineers, New Haven, CT.
YEE D and Bradford J (1999) Employment Density Study, Canadian METRO Council Technical Report, April 6 1999.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]