Shah Jamal Alam, Ruth Meyer, Gina Ziervogel and Scott Moss (2007)
The Impact of HIV/AIDS in the Context of Socioeconomic Stressors: an Evidence-Driven Approach
Journal of Artificial Societies and Social Simulation
vol. 10, no. 4 7
<https://www.jasss.org/10/4/7.html>
For information about citing this article, click here
Received: 01-Mar-2007 Accepted: 18-May-2007 Published: 31-Oct-2007
 Abstract
Abstract| Table 1: Agent's characteristics | |
| Attribute | Possible values |
| Gender | Female; male |
| Age Group | Child [0-16); adult [16-45); senior [45-onwards) years |
| Health Status | Well/ok; HIV/AIDS; old-age sickness; disabled |
| Life Expectancy | Sampled from Normal Distribution with values of mean expected age (56 years) and standard deviation (10 years), as abstracted from the demographic data. |
| Hunger Status | Fully-fed; half-fed; not-fed |
| HIV/AIDS Incidence (t: year) ← Gamma (alpha, beta) |
where the distribution parameter values for alpha and beta used in the reported simulation runs are 12 and 1.25 respectively. The values are taken from Salomon et al. (2000) based on their study in the region.
| Village-labour-income ← Normal (100, 25) |
The values have been found plausible from the anecdotal accounts only. Use of the normal distribution is an otherwise unvalidated model's assumption.
| Table 2: Available grants | |
| Grant Type | Specification |
| Child Support Grant | For children under the age of 7. |
| Disability Grant | For adults suffering from HIV/AIDS. Not all qualifying adults apply for this grant as there is a social stigma when an individual is known to be infected. |
| Old-age Pension | Seniors may receive this grant from the age of 55 for women and the age of 60 for men. |
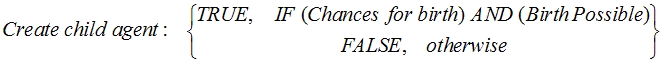
|
| Birth Possible ← If (mother is well or HIV+ and fertility exists) and at least one year passed since last birth) |
| Table 3: Outline of the main flow of a simulation run in the model. Pseudocode for the procedures which have not been discussed in this section are presented in the appendices B and C | |
Initialization:
1. Set a proportion {parameter} of adult male agents on migration
//Mostly, adult agents go on migration
2. Assign a proportion {parameter} of households to members of randomly chosen funeral clubs
Main Schedule: Runs for n time steps.
1. For each agent ∈ Agents
call agent.step (current_time) //agent's step function
//Introduce HIV incidence to uninfected agents in the population.
2. call HIV_Incidence (current_time)
3. purgeDeadAgents() //remove all dead agents
4. call allocate_grants_to_eligible_agents ()
5. For each household ∈ Households_with_no_Guardians
//accommodate dependents of dissolved household
call purgeHouseholds ()
6.i. If ((there exists a couple in a household)
and (can afford a new house))
call create_new_household (couple)
6.ii. For each household ∈ Households
For each couple ∈ household
If (couple.birth_Possible())
Call create_child_agent (current_time)
7. For each household ∈ Household
call household.step (current_time) //household's step function
8.i. For each stokvel ∈ Stokvels //(savings clubs)
call stokvel.step() //savings club rotation
8.ii. For each club ∈ Funeral_Clubs
call club.step() //give money to requesting households
9. If (Marriage_Probability)
//find random male and female from two different households
//and create new couple.
call marriage ()
10. End
|
|
|
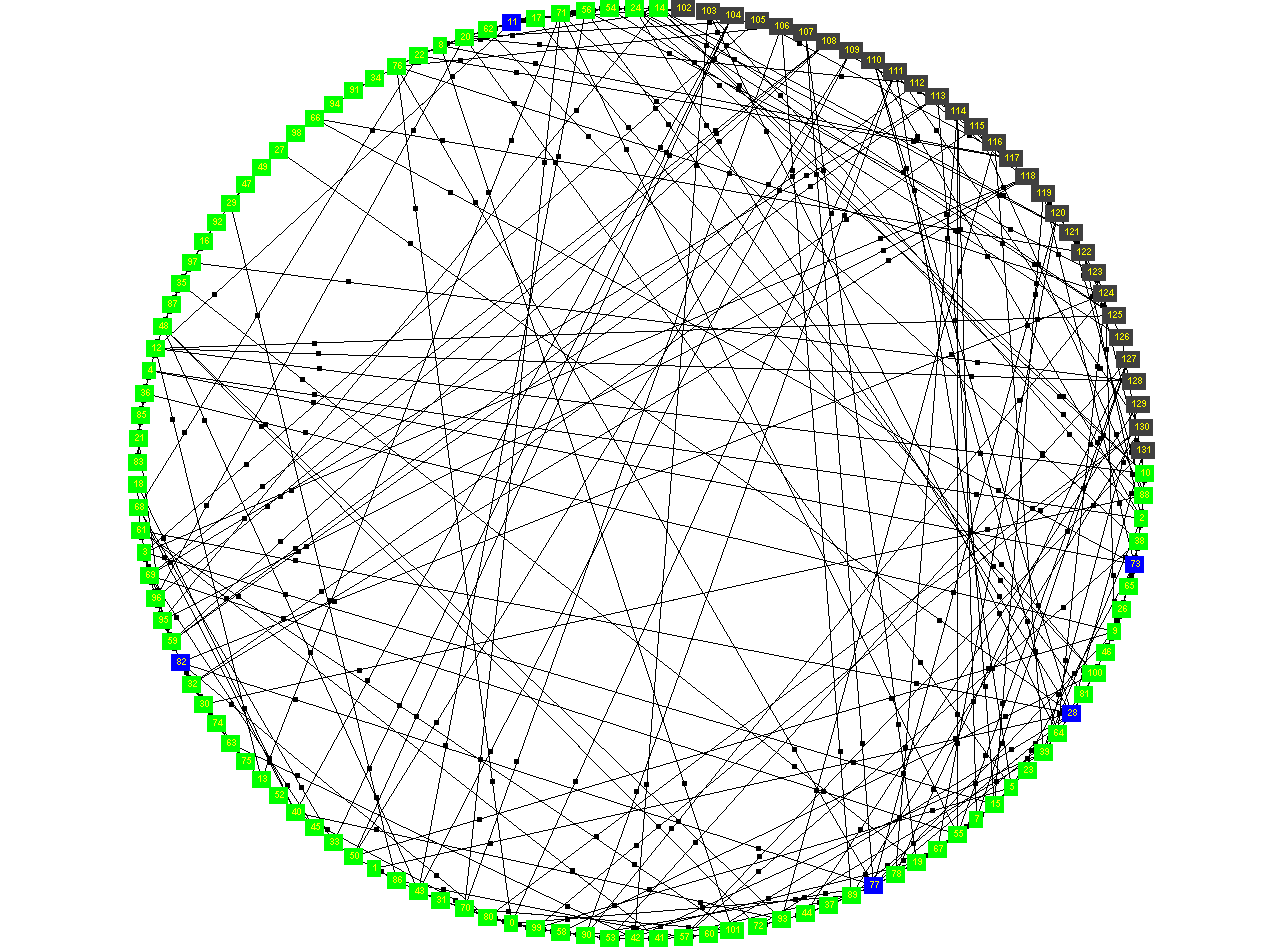
| Figure 1. Example of a social neighbourhood space of the village households in the model. The blue squares indicate households that have accommodated members of dissolved households |

|
| Figure 2. Example of the adult agents' friend network |
|
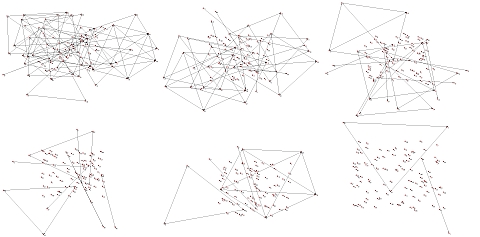
| Figure 3. Snapshots of the savings club memberships |
If (there are children in the household)
AND (household members are hungry)
AND (household can afford travel expenditure)
Then (decide to migrate)
|
|
| Figure 4. Two examples of an extended family network at the start of a simulation run: (left) when households build links purely on the basis of marriages during the simulation; (right) random initial assignment of households in moieties |
|
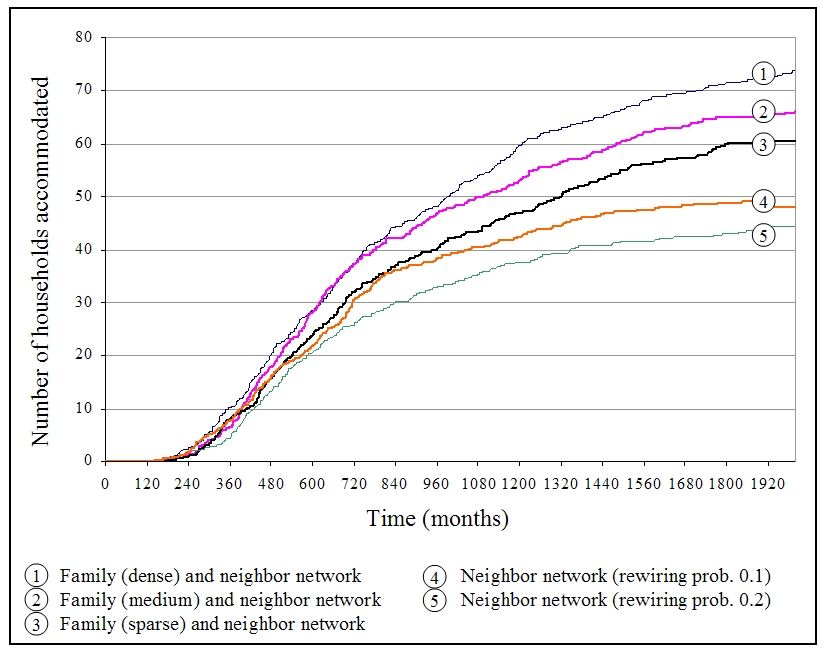
| Figure 5. Accommodation of dissolved households in five different settings |
|
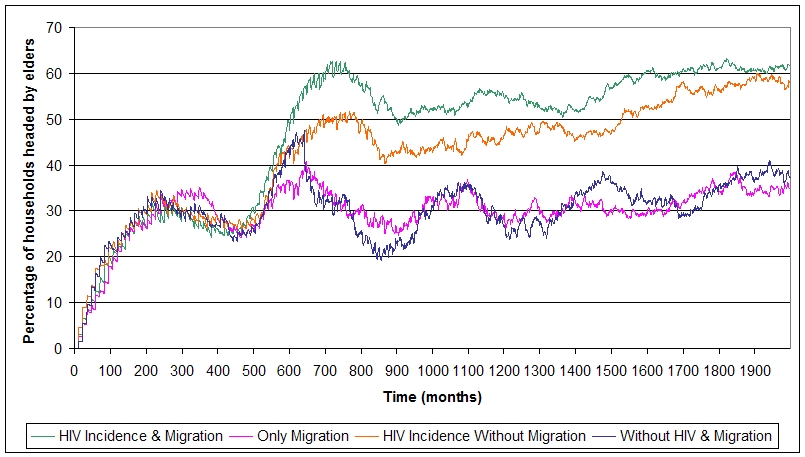
| Figure 6. Effect of HIV/AIDS incidence and migration on the age of household heads |
|
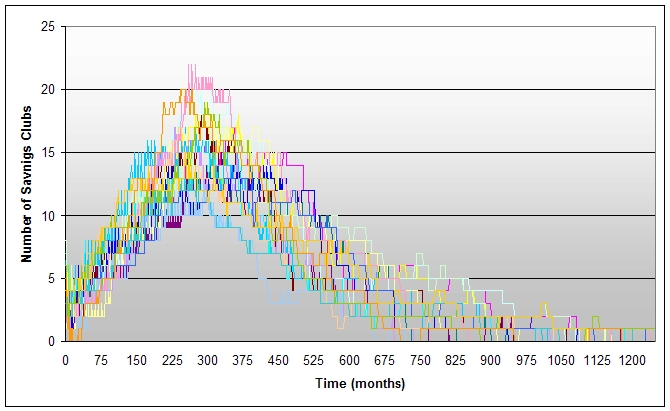
| Figure 7. Sample of the 20 simulation runs within the same scenario showing the variability in the number of savings clubs formed over time |
|
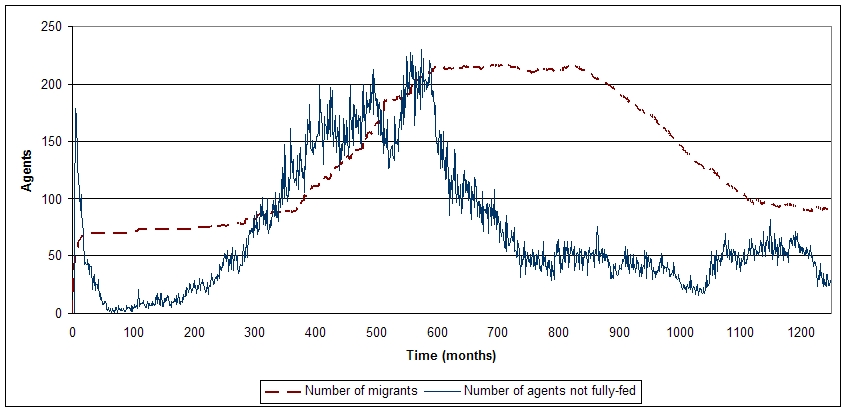
| Figure 8. Time series of agents migrating and agents going hungry during the simulated runs |
|
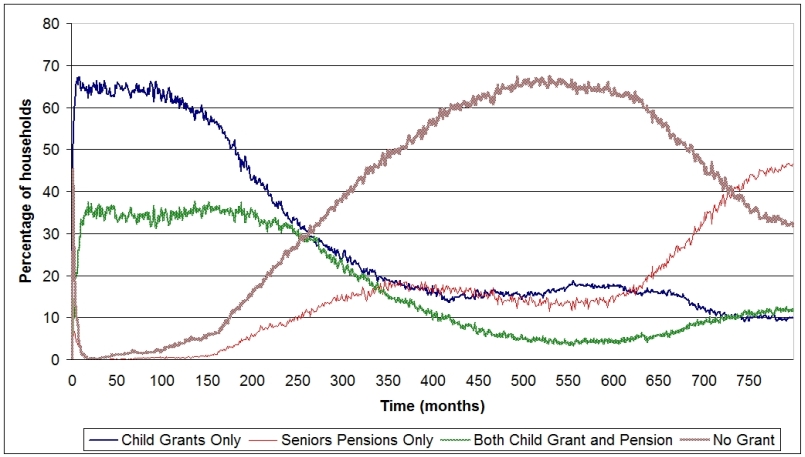
| Figure 9. Contributions of child grants and old-age pensions to the households' accumulated income, for 100 households. X-axis: time in months, y-axis: percentage of households |
|
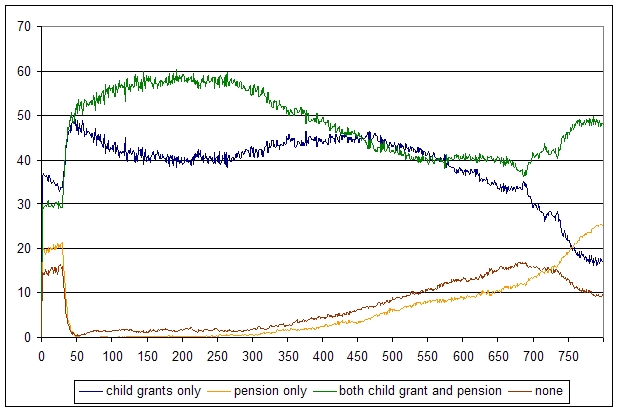
| Figure 10. Contributions of child grants and old-age pensions to the households' accumulated income, for 100 households. X-axis: time in months, y-axis: percentage of households |
|
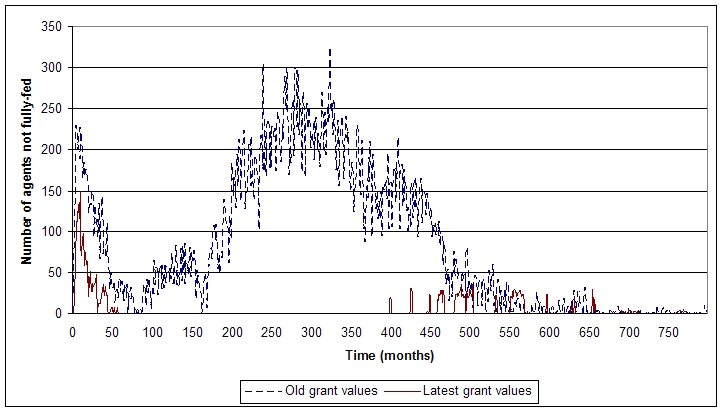
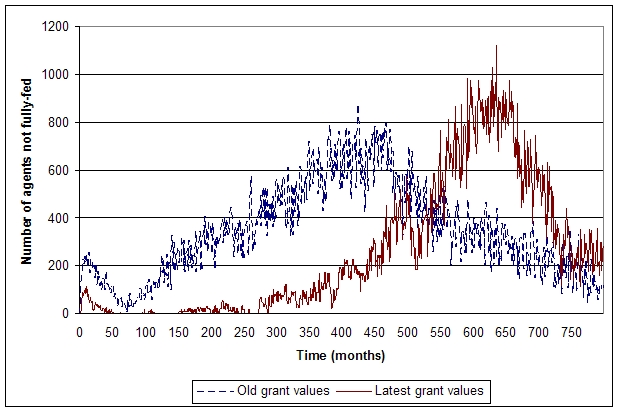
| Figure 11. Percentage of agents not fully-fed with prevalence of HIV/AIDS, for old state grant values and the latest grant values from the 2007 budget |
|
| Figure 12. Percentage of agents not fully-fed without HIV/AIDS, for old state grant values and the latest grant values from the 2007 budget |
2 CAVES (Complexity, Agents, Volatility, Evidence and Scale): http://caves.cfpm.org
3 RADAR: "Rural AIDS and Development Action Research programme comprises clinical and social intervention research on HIV/AIDS, with an emphasis on developing model approaches that are appropriate and relevant to the rural African context. It is founded on the premise that the HIV epidemic is rooted in biological, behavioural and social processes—reflecting complex and dynamic relationships within countries and between them. Generating an effective response will therefore require a similar diversity of strategies at the level of individuals and populations. RADAR is based in the Limpopo (formerly Northern) Province of South Africa at the Health Systems Development Unit. The programme is a collaboration between the School of Public Health at the University of the Witwatersrand and the London School of Hygiene and Tropical Medicine." http://www.wits.ac.za/radar/
4 Repast Agent Simulation Toolkit: http://repast.sourceforge.net/
5 Java Expert System Shell: http://www.jessrules.com/jess/
6 Pajek (Program for Large Network Analysis): http://vlado.fmf.uni-lj.si/pub/networks/pajek/
7 see e.g. AVERT (AIDS & HIV Charity) http://www.avert.org/pregnancy.htm
8 Food and Agriculture Organization (FAO) http://www.fao.org
9 The idea of 'facilitators' was introduced in the model in order to represent individuals who possess higher coordinating skills and thus play the role in kick-starting stokvels in the model.
10 Our choice of 100 households is because it approximates a village's population in the region.
11 A re-wiring probability of 0.2 results in a low clustering coefficient score and a low average path length. Thanks to the anonymous referee for pointing this out.
12 South Africa budget 2007: http://www.sars.gov.za/budget/documents/budget/2007/guide.pdf
ALAM, S.J., Meyer, R. and Ziervogel, G. (2006), Modelling the Socio-Economic Impact of HIV/AIDS in South Africa, in Proceedings of the First World Congress on Social Simulation (WCSS'06), vol. 2, pp. 281-288, Kyoto, Japan
AXTELL, R.L. (2002), Non-cooperative dynamics of multi-agent teams, in Proceedings of the First International Joint Conference on Autonomous Agents and Multiagent Systems, (AAMAS 2002), pp. 1082-1089, The ACM Press
BHARWANI, S., Bithell, M., Downing, T.E., New, M., Washington, R. and Ziervogel, G. (2005), Multi-agent modelling of climate outlooks and food security on a community garden scheme in Limpopo, South Africa, Philosophical Transactions of the Royal Society B., vol. 360. pp. 2183-2194.
BARRETEAU, O. and Bousquet, F. (1999). "Jeux de rôles et validation de systèmes multi-agents". In Gleizes M-P and Marcenac P (eds.) Ingénierie des systèmes multi-agents, actes des 7èmes JFIADSMA, Hermès.
BARTHELEMY, O.T. (2006), Untangling Scenario Components with Agent Based Modelling: an Example of Social Simulations of Water Demand Forecasts. Doctoral Thesis, Manchester Metropolitan University, Manchester, UK (available at: http://cfpm.org/cpmrep163.html)
BRUNNER, D. (2002), Labour Migration and HIV/AIDS in Southern Africa, International Organisation for Migration Regional Office for Southern Africa, South Africa
CARLEY, K. (2003), Dynamic Network Analysis, in Breiger, Carley, and Pattison, (eds.), Dynamic Social Network Modelling and Analysis: Workshop Summary and Papers, Committee on Human Factors, National Research Council, National Research Council, pp. 133-145.
CASE, A., Hosegood, V. and Lund, F. (2003), The reach of the South African Child Support Grant: Evidence from KwaZulu-Natal, CSDS Working Paper No. 38, October 2003, ISBN No. 1-86840-513-3, South African Regional Poverty Network (SARPN), http://www.sarpn.org.za/
CLARK, S.J., Collinson, M.A., Kahn, K., Drullinger, K. and Tollman, S.M. (2006), Returning Home to Die: Urban to Rural Migration and Mortality in Rural South Africa, Scandanavian Journal of Public Health, vol. 35, pp. 35 - 44.
DRIMIE, S. (2002), The Impact of HIV/AIDS on Rural Households and Land Issues in Southern and Eastern Africa, Food and Agricultural Organization, Sub-Regional Office for Southern and Eastern Africa August 2002, http://www.fao.org
DRIMIE, S. and Ziervogel, G. (2006), Food security in Sekhukhune, FIVIMS Food Security Brief, http://www.fivims.net
DOWNING, T.E., Moss, S. and Pahl-Wostl, C. (2000), Understanding Climate Policy Using Participatory Agent-based Social Simulation, in Moss, S. and Davidsson, P. (eds.), Multi Agent Based Simulation (MABS'00), Lecture Notes in Artificial Intelligence, vol. 1979, pp. 198-213, Berlin et al.: Springer-Verlag
EDMONDS, B. and Moss, S. (2005), From KISS to KIDS: an 'anti-simplistic' modelling approach, in Davidsson, P., et al. (eds.), Multi Agent Based Simulation (MABS'04), Lecture Notes in Artificial Intelligence, vol. 3415, pp. 130-144, Berlin et al.: Springer-Verlag
ERNST, A., Krebs, F. and Zehnpfund, C., 2006, Dynamics of task oriented agent behaviour in multiple layer social networks, in Proceedings of the First World Congress on Social Simulation (WCSS'06), Kyoto, Japan
FOSTER, G. (2005), Under the Radar—Community Safety Nets for Children Affected by HIV/AIDS in Poor Households in Sub-Saharan Africa, United Nations Research Institute for Social Development (UNRISD),
http://www.sarpn.org.za/documents/d0001830/Unrisd_children-HIV_Jan2005.pdf
GILBERT, N. and Troitzsch, K.G. (2005), Simulation for the social scientist (2nd ed.), Milton Keynes: Open University Press.
HANDCOCK, M.S., Jones, J.H., and Morris, M. (2003) On "Sexual contacts and epidemic thresholds," models and inference for sexual partnership distributions. Working Paper #31, Center for Statistics and the Social Sciences, University of Washington, USA http://www.csss.washington.edu/Papers/wp31.pdf
HEUVELINE, P. (2004), Impact of the HIV epidemic on population and household structure: the dynamics and evidence to date, AIDS, vol. 18 (suppl. 2), pp. 45-53
HEUVELINE, P., Sallach, D., and Howe, T. (2003), The Structure of an Epidemic: Modelling AIDS Transmission in Southern Africa', in Proceedings of Symposium on Agent-based Computational Modelling, Vienna, Austria
KALIPENI, E., Craddock, S., Oppong, J.R. and Ghosh, J. (eds.) (2004), HIV&AIDS in Africa: Beyond Epidemiology, Oxford: Blackwell Publishing.
MAHLOELE, M.A. (2005), Nutritional status of families in Sekhukhune District with or without a nutrition intervention, Master thesis, University of Pretoria
MOSS, S. (1998), Critical Incident Management: An Empirically Derived Computational Model, Journal of Artificial Societies and Social Simulation, 1(4)1 https://www.jasss.org/1/4/1.html
MOSS, S. and Edmonds, B. (2005a), Towards Good Social Science, Journal of Artificial Societies and Social Simulation, 8(4)13 https://www.jasss.org/8/4/13.html
MOSS, S. and Edmonds, B. (2005b), Sociology and Simulation: Statistical and Qualitative Cross-Validation, American Journal of Sociology, vol. 110, no.4, pp. 1095-1131, Chicago: The University of Chicago Press
POKU, N.K. and Whiteside, A. (eds.) (2004), The Political Economy of AIDS in Africa, UK: Ashgate Publishing.
POSEL, D. (2001), How Do Households Work? Migration, the Household and Remittance Behaviour in South Africa. Social Dynamics, vol. 27, no. 1, pp. 167-192, Centre for African Studies, The University of Cape Town
POSEL, D. and Casale, D. (2003), What has been happening to Internal Labour Migration in South Africa, 1993-1999? Development Policy Research Unit, Working Paper 03/74, ISBN 0-7992- 2173-2.
PRONYK, P. (2002), Social Capital and the HIV/AIDS epidemic in rural South Africa: The New Magic Bullet?, The Department of Infectious and Tropical Diseases, The London School of Hygiene & Tropical Medicine, London http://www.wits.ac.za/radar/PDF%20files/socialcapital_HIV.PDF
QUINLAN, T., Ziervogel, G., and O'Brien (2005), Assessing Vulnerability in the Context of Multiple Stressors: The Southern Africa Vulnerability Initiative (SAVI), in Proceedings of the IFPRI Conference, Durban, South Africa
RADAR (2005), The RADAR IMAGE study – intervention with microfinance for AIDS and gender equity. http://wits.ac.za/radar/IMAGEstudy.htm
SALOMON, J.A., Gakidou, E.E, Murray, C.J.L. (2000), Methods for Modelling the HIV/AIDS Epidemic in Sub-Saharan Africa. Geneva, World Health Organization, GPE Discussion Paper Series: No. 3, EIP/GPE/EBD, https://www.who.int/healthinfo/paper03.pdf
SEAGER, J., Ganyaza-Twalo, T. and Tsiliso, T. (2005), Development of a Conceptual Framework to Help Understand the Interactions Between Poverty and HIV/AIDS at the Household Level, International Union for the Scientific Study of Population (IUSSP) Seminar on "Interactions between Poverty and HIV/AIDS", 12-14 December 2005, Cape Town, South Africa
STEINBERG, M., Johnson, S., Schierhout, G. and Ndegwa, D. (2002), How Households Cope With The Impact Of The HIV/AIDS Epidemic: A Survey Of Households Affected by HIV/AIDS in South Africa, The H.J. Kaiser Family Foundation
TEWELDEMEDHIN, E., Marwala, T., and Mueller, C. (2004), Agent-Based Modelling—A Case Study in HIV Epidemic. Proc. of 4th Int'l Conference on Hybrid Intelligent Systems (HIS'04), IEEE Xplore, pp. 154-159, IEEE Press
DU TOIT, A. and Ziervogel, G. (2004), Vulnerability and Food Insecurity—Background concepts for informing the development of a national FIVIMS for South Africa. http://www.agis.agric.za/agisweb/FIVIMS_ZA
TRIEGAARDT, J.D. (2005), The Child Support Grant in South Africa: a social policy for poverty alleviation?, International Journal of Social Welfare, vol. 14, pp. 249-255, Oxford: Blackwell Publishing
UNAIDS (2005), Sub-Saharan African Fact Sheet, UNAIDS Epidemic Update 2005 http://data.unaids.org/Publications/Fact-Sheets04/FS_SubSaharanAfrica_Nov05_en.pdf
UNAIDS (2006), Report on the global AIDS epidemic. http://www.unaids.org
VERHOEF, G. (2001), Informal Financial Service Institutions for Survival—African Women and Stokvels in Urban South Africa, 1930-1998. Enterprise & Society 2, pp. 259-296.
VERMAAK, N. J. (2001), Rural financial schemes' contribution to community development, Community Development Journal, vol. 36, no. 1, pp. 42-52, Oxford: Oxford University Press
WALKER, J.R. (2006), Economic Perspectives on Family and Migration, http://www.ssc.wisc.edu/~walker/research/ma_conf_walker.pdf
WATTS, D.J. (2003), Six Degrees: The Science of a Connected Age, W. W. Norton & Company.
WERTH, B. and Moss, S. (2007), Modelling Migration in the Sahel: An alternative to cost-benefit analysis, in Terano, T., Takahashi, S., Sallach, D. and Rouchier, R. (eds.), Advancing Social Simulation, Berlin et al.: Springer-Verlag.
XIONG, L. and Ma, X. (2007), Forecasting China's Medical Insurance Policy for Urban Employees Using a Microsimulation Model, Journal of Artificial Societies and Social Simulation 10(1)8 https://www.jasss.org/10/1/8.html
YOUNGER, Y. (2005), Violence and revenge in egalitarian societies, Journal of Artificial Societies and Social Simulation, 8(4)11 https://www.jasss.org/8/4/11.html
ZIERVOGEL, G. (2005), Non Governmental Organisations in Vhembe, Limpopo Province, South Africa: Their emergence from and consequent changes to social networks, Briefing Note, CAVES Project available at http://cfpm.org/caves/CAVESWiki/KnowledgeBase
ZIERVOGEL, G. et al., (2005), UNRAVEL—Understanding resilient and vulnerable livelihoods in Malawi, South Africa and Zambia. Final Research Report, University of Cape Town, South Africa, September 2005.
ZIERVOGEL, G, Bharwani, S. and Downing, T.E. (2006a), Adapting to climate variability: pumpkins, people and policy. Natural Resource Forum, 30, 294-305.
ZIERVOGEL, G., Taylor, A., Thomalla, F., Takama, T. and Quinn, C. (2006b) Adapting to climate, water and health stresses: insights from Sekhukhune, South Africa, Stockholm Environmental Institute Report, Oxford, UK.
ZIERVOGEL, G. (forthcoming), Stresses, Shocks, Coping and Intervention Strategies affecting households (draft available on request).
//probability that an adult HIV/AID agent gets this grant DISABILITY_GRANT_PROBABILITY = 0.10 PENSION_AGE_FEMALE = 55 years PENSION_AGE_MALE = 60 years //the following is same for both female and male agents in the model MEAN_LIFE_EXPECTANCY = 75 years STANDARD_DEVIATION_LIFE_EXPECTANCY = 5 years //Households initialized with wealth chosen randomly from this range: MIN_STARTING_WEALTH = 500 Rand MAX_STARTING_WEALTH = 1500 Rand FUNERAL_CLUB_FEE = 250 Rand //this is for an adult agent MIN_MONEY_TO_FEED = 45 Rand MAX_MONEY_TO_FEED = 65 Rand //Grant values: DISABILITY = 300 Rand PENSION_GRANT = 560 Rand CHILD_GRANT = 125 Rand ORPHAN_GRANT = 175 Rand MARRIAGE_AGE_UPPER_LIMIT = 45 years //Remittance value of the migrant agents chosen from Normal distribution MEAN = 200 Rand; STD_DEV = 50 Rand //the 'grace period' for the number of months a household might benefit from a funeral club without being able to paying the dues FUNERALCLUB_GRACE = 6 months //HIV-infected agents' health starts to deteriorate only after some time //could be 6 months - 4 years depending upon the nature of the HIV variant //we have kept it fixed. INFECTED_LAG = 18 months //the birth rate is 0.3 per person-year in many of the most affected BIRTH_PROBABILITY = 0.25 //cost for funeral / burial ... can be as high as 5000 Rand FUNERAL_COST = 2500 Rand PROPORTION_OF_FACILITATORS_AT_START = 20% MINIMUM_MEMBERS_REQUIRED_FOR_SAVINGS_CLUB = 5 HEALTH_EXPENDITURE_FOR_SINGLE_AGENT = 100 Rand
| Table B1: Pseudocode for initiating and joining a savings club and the schedule | |
Assumptions:
1. Only women household heads join the savings club (stokvel).
2. Some agents are facilitators ≤ MAX_FACILITATORS: having, e.g. able to stimulate creating a club etc.
Savings Clubs (Stokvels) Creation Schedule:
1. For all facilitator ∈ Facilitators | isHouseholdHead (facilitator) ∧ joinClub (facilitator)
a. For each agent ∈ Agents | isHouseholdHead(agent) ∧ {facilitator.Friend(agent) ∨ facilitator.neighbor(agent)}
b. sendInvitation(facilitator, agent)
2. For each agent ∈ Agents | isHouseholdHead(agent)
a. handleInvitation(sender); where sender is the facilitator
b. If (invitation-accepted) sendAcceptance(agent, sender); else sendRejection(agent, sender)
3. For each facilitator ∈ Facilitators |isHouseholdHead(facilitator)
If (#acceptances ≥ MIN_CLUB_SIZE) create new savings club
handleInvitation: on receiving the invitation from an facilitator agent to join a new savings club
If {(joinClub(facilitator) ∧ !memberSavings) sendAcceptance; Else sendRejection
joinClub: a household head agent's decision to join a savings club or not;
If (household wealth ≥ SAVINGS_CLUB_FEE) join club
Savings Club Rotation Schedule:
1. For each member ∈ Members of the club
a. If {isDead(member) ∨ isPulledOut(member) remove member
b. If { not (|Members| ≥ MIN_CLUB_SIZE) } finish club
c. amount ← amount + member's contribution
2. next candidate gets the lump sum amount
|
|
| Table B2: Pseudocode for the funeral club methods | |
Joining and paying the contributions at a funeral club:
1. A Household joins when there is an adult bereavement due to HIV/AIDS; membership is permanent.
2. Dues (set fixed) are paid monthly. In case of consecutive default for 'n' months, aid is not given.
Funeral Club Schedule:
1. Receive request for payment from members.
2. If possible, pay all requesting members the funeral cost
Else distribute the available funds equally.
|
|
| Table C1: Estimated energy requirements expressed as a percent of Adult Male. Calculated based on a Tsimane' body weight data, and the FAO/WHO/UNU (1985) equations for estimating energy needs | |||||||
| Sex/: Value | Adults (18-59 yr) | 0-2 yr | 3-5yr | 6-9 yr | 10-13 yr | 14-17 yr | Elderly (60+ yr) |
| Males/% of adult male | 100 | 33 | 48 | 64 | 74 | 87 | 62 |
| Females: % of adult female | 75 | 35 | 53 | 53 | 66 | 70 | 57 |
Process: Agent's step function (Agent: agent)
If (agent is a year older at current tick)
Then update agent's age
call update_health_status(agent)
If (agent is not dead)
If (fit_for_labour(agent))
If (should_migrate) Then set_migrated(agent)
Else If (gets_village_labour) Then set_onLabour(agent)
If (last_try_to_join_stokval > 6 months) Then try_join_stokvel
End
Process: Updating agent's health status (Agent: agent)
If (health_status is HIV) AND (time_since_infected ≥ infected_lag)
Then fast-decay (health); using sigmoid curve
Else If (agent is old)
If (health-count is Weak) Then set health_status ← old-age-sickness
else set health_status ← disabled
else if (agent is adult) or (agent is child)
if (health-count is weak) then set health_status ← illness
end
Process: feeding household agents (agent: household head)
for all agents on labour or migration
set feed-status ← full-fed
;now for the rest of the household
for all agents currently in the household
;maize price is set to be 3rand/kg; 10kg assumed for adult male/month
food-requirement ← add (agent(food-requirement * maize-price))
if ((can_afford (food-requirement)
and (not member-funeral-club)
or ((member-funeral-club) and (can_afford (food-requirement and funeral-club-fee)))
set feed-status ← full-fed
else if ((member-funeral-club)
and (food-requirement + funeral-club-fee ≥ household-wealth))
for all child agents in the household
set feed-status ← full-fed
for all other agents in the household
if (can_afford 'half-feeding' for all)
set feed-status ← half-fed
else
to agents as possible: set feed-status ← half-fed
to the rest: set feed-status ← not-fed
end
Process: borrow food (agent: adult hungry agent)
for all agents in the friendship-network
if (ask (friend) and friend.can_feed(agent)
set feed-status ← half-fed
;procedure: can_feed (agent: borrower)
if house.haswealth
;lend money to half-feed the borrower agent
then feed (borrower, half-fed)
end
Process: fertility criteria (agent: adult female; current_tick)
; this is an abstract implementation
pre-condition: got infected from hiv at time: infected_tick
time-difference ← current_tick - infected_tick
if (time-difference less than 2.5 years)
then return (chance for fertility: 100%)
else if (time-difference less than 5 years and greater than 2.5 years)
then return (chance for fertility: 75%)
else if (time-difference less than 7.5 years and greater than 5 years)
then return (chance for fertility: 55%)
else return (chance for fertility: 40%)
end
Process: fit_for_labour (agent: agent; current_tick: return boolean)
;this rule is based on an arbitrary assumption
if ((agent is old and health_status is not hiv)
or ((health_status is hiv) and (time since hiv infection less than infected_lag))
then return true
else return false
end
Process: household step function (household: household)
for all agents in the household
update_cash_in_hand(receive_income(agent))
; deduct household's wealth for food expenditure
call feed_members
call deduct_health_expenditure
; for funeral clubs and stokvels if it is a member
call deduct clubs_fees
end
Process: deduct health expenditure (household: household; current_tick)
for all agents in the household
if ((health_staus: hiv and time since hiv infection greater than infected_lag)
or (health_status is illness or old-age-sickness))
call deduct_wealth(health_expenditure)
end
Process: Deduct funeral cost (Household: household; is_Bereaved: true)
; This is an arbitrary assumption
If (cash_in_hand is twice the funeral_cost)
; I am wealthy so I will have a full-fledged funeral arrangement
Then call deduct_wealth(funeral_cost)
Else
; cost to be born by the household and the extended family network collectively
cost ← call calculate_lesser_cost
call borrow_funeral_cost(cost)
end
Process: Borrow funeral cost (Household: household; cost)
If (cannot bear cost)
Then for all relative_household in the extended_family_network
call ask_contribution_for_funeral (relative_household)
End
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]