Roy Wilson (2007)
Simulating the Effect of Social Influence on Decision-Making in Small, Task-Oriented, Groups
Journal of Artificial Societies and Social Simulation
vol. 10, no. 4 4
<https://www.jasss.org/10/4/4.html>
For information about citing this article, click here
Received: 24-Mar-2007 Accepted: 15-Jul-2007 Published: 31-Oct-2007
 Abstract
Abstract|
Observable |
|
Unobservable (inferred) |
|
Unobservable (inferred) |
|
Communicative acts |
→ |
Social relations |
→ |
Expectation states |
|
↑ |
|
|
|
↓ |
|
|
← |
|
← |
|
| Figure 1. The social system | ||||
these groups have a set of beliefs about 'human nature' and the organization of work and family that allow the participants to interpret the 'facts' in the human relations case. (Meeker 1994)Of course, not all such groups exhibit consensus regarding goals and values: EST is not applicable to these groups.
|
a |
→ |
X(+) |
→ |
Y(+) |
→ |
Z(+) |
→ |
T(+) |
|
|
|
- |
|
|
|
|
|
|
|
d |
→ |
X(-) |
→ |
Y(-) |
→ |
Z(-) |
→ |
Z(-) |
| Figure 2. A social-psychological definition of the situation | ||||||||
| f(p(1) ∪ … ∪ p(n)) = 1 - [(1 - f(p(1))) × … × (1 - f(p(n)))] | (1.1) |
The value of e(x) is computed as the sign of the paths in the combination times the strength of combination of paths from x to the task outcomes. e(a) > 0, so (via equation (1.2)) the simple expectation state associated with a is (collective) task success. Similarly, because e(d) < 0, d is linked by the simple expectation state to (collective) task failure. Note that the prefixed sign in equations (1.2) and (1.3) is determined by the sign of the paths leading from the actor to the task outcome.
| e(a) = +1 × (1 - [(1 - f(4) × (1 - f(5))]) = +0.1826 | (1.2) |
| e(d) = -1 × (1 - [(1 -f(4)) × (1 - f(5))]) = -0.1826 | (1.3) |
| ae(x) = 1 – 0.8174k | (1.4) |
| ae(x-) = -(1 - 0.8174j) | (1.5) |
| ae(x) = 0.8174j - 0.8174k | (1.6) |
|
a ↓ d → z ↑ w | |
| Figure 3. Sample precedence graph | |
| ae(d) = 0.81742 - 0.81741 = -0.1493 | (1.7) |
| Table 1: Initial aggregate expectation states derived from Figure 3 | |||
|
|
k pairs of positive paths |
j pairs of negative paths |
ae(x) |
|
|
(In degree of actor node) |
(Out degree of actor node) |
|
|
a |
1 |
0 |
+0.1826 |
|
w |
1 |
0 |
+0.1826 |
|
z |
0 |
1 |
-0.1826 |
|
d |
1 |
2 |
-0.1493 |
| if ΣB(i, a, c)/5 < 0.5 then O(i, c) = 0 else O(i, c) = 1 | (1.8) |
| δ = Δ(ae(x), ae(y)) | (1.9) |
| num = e(0.472 + 0.632 × δ) | (1.10) |
| p(y, S) = num / (num + 1) | (1.11) |
| r = p(d, S) × B(i, d, c) | (1.12) |
| s = [1 - p(d, S)] × B(i, a, c) | (1.13) |
| B(u, d, c) = r + s | (1.14) |
| if ΣB(f, a, c) / 5 < 0.5, then O(f, c) = 0 else O(f, c) = 1 | (1.15) |
/**
* Each object of this class represents a Person. A Person is conceived as a
* semi-autonomous entity and is represented by a CSProcess. CSProcesses
* communicate over channels.
*
*/
public class Person extends CommNode implements ISocialStructure {
private SocialStructure _socialStructure;
private Crew _socialStructureCrew;
private TurnCrew _turnCrew;
final CSTimer timer = new CSTimer();
/**
* @param nodeId
* @param simParameters
* @param chanParameters
* @param belief
*/
public Person(
int nodeId,
SimParameters simParameters,
ChanParameters chanParameters,
Belief belief) {
super(nodeId, simParameters, chanParameters, belief);
_socialStructure = _simParameters.get_socialStructure();
_socialStructureCrew = _simParameters.get_socialStructureCrew();
_turnCrew = _simParameters.get_turnCrew();
}
// Each actor competes for a conversational turn
private synchronized boolean is_my_turn() {
boolean retval = false;
_socialStructureCrew.startRead();
int current_x = _socialStructure.get_current_x();
int current_y = _socialStructure.get_current_y();
_socialStructureCrew.endRead();
if (current_x == _my_nodeId) {
_tgt_nodeId = current_y;
retval = _turnCrew.claim(_my_nodeId);
}
return retval;
}
// simulate processing of incoming message
public void simulate_reader(int other_actor) {
_turnCrew.release();
timer.sleep(_simParameters.get_worktime(_my_nodeId));
_socialStructureCrew.startRead();
double ps_focal = _socialStructure.compute_PS(other_actor, _my_nodeId);
_socialStructureCrew.endRead();
_belief.update(_my_nodeId, other_actor, ps_focal);
}
// simulate formulation of outgoing message
public void simulate_writer(String msg) {
timer.sleep(_simParameters.get_worktime(_my_nodeId));
write_msg(update_msg(_normal_msg_out));
}
// Each actor is modeled as a computational process
public void run() {
Message msg_in = null, msg_out = null;
// Once initiated, run until 'poison' received from upstream
while (!_poison_rcvd) {
// If there is a message, read it and handle it
if (_chanParameters.get_medium2person(_my_nodeId).pending()) {
msg_in = read_msg(_simParameters.get_pkt_src_type());
_poison_rcvd = false;
if (msg_in.is_Poison()) {
// Forward the poison downstream
msg_out = construct_msg_out(ICommNode.SEND_POISON);
msg_out.set_content(_belief.get_datum_my_nodeId());
write_msg(msg_out);
_poison_rcvd = true;
}
simulate_reader(msg_in.get_src_nodeId());
}
if (!_poison_rcvd && is_my_turn()) {
simulate_writer("Writer Cognition");
}
}
}
}
|
| Figure 4. The Person class |
| Table 2: Control variables and their values | |
|
Variable |
Value |
|
interactions |
375 per meeting |
|
lifeThinkTime |
6.4 seconds |
| Table 3: Input variables and their values | |
|
Variable |
Value(s) |
|
η |
{0.625, 0.75} |
|
π |
{0.50} |
|
θ |
{0.25} |
|
B(i, x, c) |
For each x and each c, a fixed value in [0.0, 1.0] |
|
|
|
|
B(i, c) |
Vector of initial beliefs of group members regarding A(c) |
|
status |
{(H, M, M, L, M), (H, M, M, M), (M, M, M, L, M), (H, M, M, H, M)} |
| Table 4: Correlations among the initial beliefs of actor types | |||||
|
|
Principal |
Social |
Nurse |
Teacher |
Counselor |
|
|
|
Worker |
|
|
|
|
Principal |
+1 |
|
|
|
|
|
Social Worker |
+0.124 |
+1 |
|
|
|
|
Nurse |
-0.153 |
-0.336 |
+1 |
|
|
|
Teacher |
-0.011 |
+0.082 |
-0.346 |
+1 |
|
|
Counselor |
+0.013 |
-0.012 |
-0.314 |
-0.389 |
+1 |
| Table 5: Output variables | |
|
Variable |
Description |
|
B(f, c) |
Final belief of group members regarding A(c) |
|
O(i, c) |
A(c) under static model: 1 (true); 0 (false) |
|
O(f, c) |
A(c) under process model: 1 (true); 0 (false) |
|
steps2equilibrium |
# of interactions till the social network is complete |
|
participation(x) |
# of interactions in which x addresses some y |
| Table 6: The static and process models on A(c) (over all c) | |||
|
Agree |
Disagree |
Total |
Proportion Agree |
|
2464 |
1087 |
3551 |
0.694 |
| Table 7: The static and process models on A(c): More detail | |||
|
Decision |
Runs |
Runs |
Proportion |
|
model |
yielding 1 |
yielding 0 |
yielding 1 |
|
Static |
1760 |
1791 |
0.4956 |
|
Process |
2015 |
1536 |
0.5675 |
| Table 8: Disagreement of the static and process decision models | |||
|
|
O(f, c) = 0 |
O(f, c) = 1 |
Static Total |
|
O(i, c) = 0 |
1120 |
671 |
1791 |
|
O(i, c) = 1 |
416 |
1344 |
1760 |
|
Process Total |
1536 |
2015 |
3551 |
| Table 9: Static versus process outcomes (by status) | |||||
|
|
O(i, c) |
O(f, c) = 0 |
O(f, c) = 1 |
χ2 |
% |
|
|
|
|
|
for 2 × 2 |
0 → 1 |
|
(a) (H,M,M,L,M) |
0 |
296 |
152 |
|
60.3 |
|
|
1 |
100 |
340 |
|
|
|
|
|
|
|
0.0011 |
|
|
(b) (H,M,M,M,M) |
0 |
256 |
192 |
|
61.5 |
|
|
1 |
120 |
320 |
|
|
|
|
|
|
|
4.588e–05 |
|
|
(c) (M,M,M,L,M) |
0 |
264 |
183 |
|
67.5 |
|
|
1 |
88 |
352 |
|
|
|
|
|
|
|
7.888e–09 |
|
|
(d) (H,M,M,H,M) |
0 |
304 |
144 |
|
57.1 |
|
|
1 |
108 |
332 |
|
|
|
|
|
|
|
0.0234 |
|
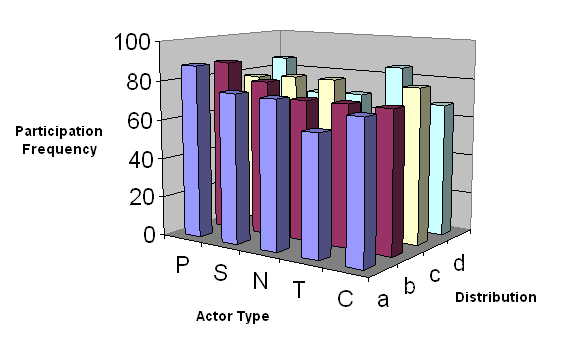
|
| Figure 5. Variation in mean participation frequency |
ABBOTT A (1988) The System of Professions. Chicago, IL: University of Chicago Press.
BALKWELL J W (1991) From expectations to behavior: An improved postulate for expectation-states theory. American Sociological Review, 56, pp. 355-369.
BALKWELL J W (1994) "Status". In Foschi, M and Lawler, E J (Eds.) Group Processes: Sociological Analyses, Chicago, IL: Nelson-Hall.
BERGER J and Cohen, B P and Zelditch Jr, M (1966) "Status characteristics and expectation states". In Berger, J and Zelditch Jr, M and Anderson B (Eds.) Sociological Theories in Progress, Boston, MA: Houghton Mifflin.
BERGER J and Norman, R Z and Zelditch Jr, M (1977) Status Characteristics and Social Interaction. New York, NY: Elsevier.
BERGER J and Wagner, D and Zelditch Jr, M (1985) "Introduction: Expectation states theory. Review and assessment". In Berger, J and Zelditch Jr, M (Eds.) Status, Rewards, and Influence, San Francisco, CA: Jossey-Bass.
BRUINS J and Ellemers, N and De Gilder, D (1999) Power use and differential competence as determinants of subordinates' evaluative and behavioural responses in simulated organizations. European Journal of Social Psychology, 29, pp. 843-870.
BRUINS J and Wilke, H A M (1992) Cognitions and behavior in a hierarchy: Mulder's power theory revisited. European Journal of Social Psychology, 22, pp. 21-40.
COLLINS R (1988) Theoretical Sociology. San Diego, CA: Harcourt Brace Jovanovich.
DAVID N and Sichman, J and Coelho, H (2005) The logic of the method of agent-based simulation in the social sciences: Empirical and intentional adequacy of computer programs. Journal of Artificial Societies and Social Simulation, 8(4).
DENNIS M L and Lenox, R D and Foss, M A (1997) "Practical power analysis for planning substance abuse prevention and services research". In Bryant, K M and Windle, M and West, S G Recent Advances in Prevention Research Methodology: Lessons from Alcohol and Substance Abuse Research, American Psychological Association, Washington, DC.
EAST I (1995) Parallel Processing with Communicating Process Architecture. London, UK: UCL Press Limited.
FARARO T J (1989) The Meaning of General Theoretical Sociology. Cambridge, UK: Cambridge University Press.
FARARO T J and Skvoretz, J and Kosaka, K (1994) Advances in E-state Structuralism: Further studies in dominance structure formation. Social Networks, 16, pp. 233-265.
FARARO T J and Butts, C (1999) Advances in generative structuralism: Structured agency and multilevel dynamics. Journal of Mathematical Sociology, 24(1), pp. 1-65.
FISEK M H and Berger, J and Norman, R Z (1991) Participation in heterogeneous groups: A theoretical integration. American Journal of Sociology, 97, pp. 114-42.
FRIEDKIN N E and Johnsen, E C (2003) Attitude change, affect control, and expectation states in the formation of influence networks. Advances in Group Processes, 20, pp. 1-29.
GLASS E V and Hopkins, K D (1996) Statistical Methods: In Education and Psychology. Needham Heights, MA: Allyn and Bacon.
GOLDBERG R R (1976) Methods of Real Analysis. New York, NY: John Wiley and Sons.
HOARE C A R (1985) Communicating Sequential Processes. Englewood Cliffs, NJ: Prentice Hall.
HUMMON N P (2000) Utility and dynamic social networks. Social Networks, 22(3), pp. 221-249.
HUMMON N P and Fararo, T J (1995) Actors and networks as objects. Social Networks, 17, pp. 1-26.
KEESING R (1981) "Theories of culture". In Casson, R (Ed.) Language, Culture and Cognition: Anthropological Perspectives, New York, NY: Macmillan.
LAWLER E J (1993) Review of The Daily Power Game by Mauk Mulder. Administrative Science Quarterly, 24(1), pp. 145-148.
LAWLER E J and Markovsky, B (1993) "Sociological social psychology: A preface". In Lawler, E J and Markovsky, B (Eds.) Social Psychology of Groups: A Reader, Greenwich, CT: JAI Press.
LEVIN J R and Serlin, R C (2000) Changing students' perspectives of McNemar's test of change. Journal of Statistics Education, 8(2).
MAYER T (1994) Analytical Marxism. Thousand Oaks, CA: Sage Publications.
MEEKER B F (1994) "Performance evaluation". In Foschi, M and Lawler, E J (Eds.) Group Processes: Sociological Analyses, Chicago, IL: Nelson-Hall Inc.
MOLM L D (1994) Dependence and risk: Transforming the structure of social exchange. Social Psychology Quarterly, 57(3), pp. 163-176.
MOLM L D (2001) "Theories of Social Exchange and Exchange Networks". In Ritzer, G and Smart, B (Eds.) Handbook of Social Theory, London, UK: Sage Publications.
SKVORETZ J and Fararo, T J (1996) Status and participation in task groups: A dynamic network model. American Journal of Sociology, 101(5), pp. 1366-1414.
SMITH-LOVIN L J and Skvoretz, J and Hudson, C G (1986) Status and participation in six-person groups: A test of Skvoretz's comparative status model. Social Forces, 64(4), pp. 992-1005.
SOWA J F (1984) Conceptual Structures: Information Processing in Mind and Machine. Reading, MA: Addison-Wesley.
WELCH P H and Austin, P D (2003) Java Communicating Sequential Processes (JCSP) Library (Release Candidate 4), Kent, UK.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]