Uri Wilensky and William Rand (2007)
Making Models Match: Replicating an Agent-Based Model
Journal of Artificial Societies and Social Simulation
vol. 10, no. 4 2
<https://www.jasss.org/10/4/2.html>
For information about citing this article, click here
Received: 12-Jan-2007 Accepted: 06-May-2007 Published: 31-Oct-2007
 Abstract
AbstractOnly when certain events recur in accordance with rules or regularities, as in the case of repeatable experiments, can our observations be tested—in principle—by anyone. We do not take even our own observations seriously, or accept them as scientific observations, until we have repeated and tested them. Only by such repetitions can we convince ourselves that we are not dealing with a mere isolated 'coincidence', but with events which, on account of their regularity and reproducibility, are in principle inter-subjectively testable. (Popper 1959)
The model makes three assumptions. First, each interaction is a Prisoner's Dilemma of a single move, thereby eliminating the possibility of direct reciprocity. Second, interaction is local, and so is the competition for scarce resources including space for offspring. Third, the traits for group membership and behavioral strategy are typically passed on to offspring, by means of genetics, culture, or (most plausibly) both.
The model is very simple. An individual agent has three traits. The first trait is a tag that specifies its group membership as one of four colors. The second and third traits specify the agent's strategy. The second trait specifies whether the agent cooperates or defects when meeting someone of its own color. The third trait specifies whether the agent cooperates or defects when meeting an agent of a different color. In this model, an ethnocentric strategy is one that cooperates with an agent of ones own color, and defects with others. Thus only one of the four possible strategies is ethnocentric. The other strategies are cooperate with everyone, defect with everyone, and cooperate only with agents of a different color. Since the tags and strategies are not linked, the model allows for the possibility of "cheaters" who can be free riders in the group whose tag they carry.
The simulation begins with an empty space of 50x50 sites. The space has wrap around borders so that each site has exactly four neighboring sites. Each time period consists of four stages: immigration, interaction, reproduction, and death.
The results of the original implementation of this model as well as the replicated version are discussed below.
- An immigrant with random traits enters at a random empty site.
- Each agent receives a initial value of 12% as its Potential To Reproduce (PTR). Each pair of adjacent agents interacts in a one-move Prisoner's Dilemma in which each chooses whether or not to help the other. Giving help has a cost, namely a decrease in the agent's PTR by 1%. Receiving help has a benefit, namely an increase in the agent's PTR by 3%.
- Each agent is chosen in a random order and given a chance to reproduce with probability equal to its PTR. Reproduction is asexual and consists of creating an offspring in an adjacent empty site, if there is one. An offspring receives the traits of its parent, with a mutation rate of 0.5% per trait.
- Each agent has a 10% chance of dying, making room for future offspring.
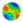
|
| Figure 1. Screenshot of the original Axelrod-Hammond model |
| Table 1: A comparison of the original model results with the first replication results (averaged over 10 runs) | |||||
| Axelrod/Hammond | Wilensky | t-values | |||
| Avg. | Std. Dev. | Avg. | Std. Dev. | ||
| Ethnocentric Consistent Actions | 88.47% | 1.64% | 88.09% | 1.10% | 0.609 |
| Cooperative Actions | 74.15% | 1.55% | 79.65% | 2.22% | -6.424 |
| Ethnocentric Genotypes | 76.31% | 3.02% | 69.14% | 4.59% | 4.127 |
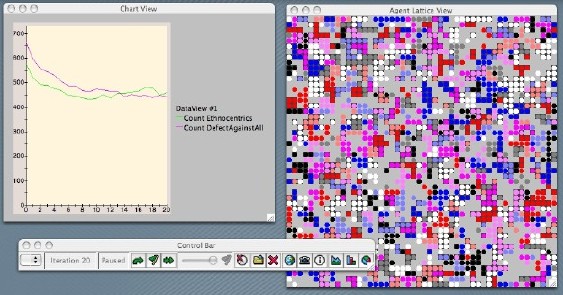
|
| Figure 2. Three agents in the ethnocentrism model |
| Table 2: Corrected Replication Results averaged over 10 runs (Model online at: http://ccl.northwestern.edu/ethnocentrism/corrected/) | |||||
| Axelrod-Hammond | Wilensky-Rand (Corrected) | t-values | |||
| Avg. | Std. Dev. | Avg. | Std. Dev. | ||
| Ethnocentric Consistent Actions | 88.47% | 1.64% | 86.97% | 2.38% | 6.017 |
| Cooperative Actions | 74.15% | 1.55% | 80.01% | 0.83% | -10.540 |
| Ethnocentric Genotypes | 76.31% | 3.02% | 67.78% | 5.81% | 4.119 |
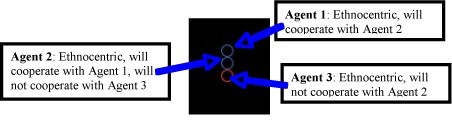
|
| Figure 3. The final model |
| Table 3: Final Replication Results averaged over 10 runs (Model online at http://ccl.northwestern.edu/ethnocentrism/final/) | |||||
| Axelrod-Hammond | Wilensky-Rand (Final) | t-values | |||
| Avg. | Std. Dev. | Avg. | Std. Dev. | ||
| Ethnocentric Consistent Actions | 88.47% | 1.64% | 88.71% | 1.97% | -0.296 |
| Cooperative Actions | 74.15% | 1.55% | 76.77% | 2.50% | -2.817 |
| Ethnocentric Genotypes | 76.31% | 3.02% | 74.73% | 4.03% | 0.992 |
| Table 4: Details To Be Included In Published Replications | |
| Categories of Replication Standards: | |
| Numerical Identity, Distributional Equivalence, Relational Alignment | |
| Distributional Equivalence | |
| Focal Measures: | |
| Identify Particular measures used to meet goal | |
| COOP, CD_GENO, CONSIS_E | |
| Level of Communication: | |
| None, Brief Email Contact, Rich Discussion and Personal Meetings | |
| Personal Meetings between replicaters and authors | |
| Familiarity with Language / Toolkit of Original Model: | |
| None, Surface Understanding, Have Built Other Models in this language / toolkit | |
| Surface familiarity with Ascape, deep familiarity with Java | |
| Examination of Source Code: | |
| None, Referred to for particular questions, Studied in-depth | |
| Mainly examined when particular questions existed about implementation details | |
| Exposure to Original Implemented Model: | |
| None, Run, Re-ran original experiments, Ran experiments other than original ones | |
| Ran the model a few times but just to get a feel for the interface | |
| Exploration of Parameter Space: | |
| Only examined results from original paper, Examined other areas of the parameter space | |
| Only examined results from original paper | |
| Table 5: Details To Be Included In Published Models | |
| Level of Detail of Conceptual Model: | |
| Textual Description, Pseudo-code | |
| Textual Description | |
| Specification of Details of the Model: | |
| Order of events, Random vs. Non-random Activation | |
| Order of events was specified in the paper form, method of activation was not clear | |
| Model Authorship / Implementation: | |
| Who designed the model, who implemented the model, and how to contact them | |
| Axelrod designed the original model, Hammond implemented the Ascape version | |
| The model was further refined by both, Email addresses for both were provided | |
| Availability of Model: | |
| Results beyond that in the paper available, Binary available, Source Code available | |
| Results beyond paper and source code available on website | |
| Sensitivity Analysis: | |
| None, Few key parameters varied, All parameters varied, Design of Experiment Analysis | |
| In the paper a few parameters were varied, but many were varied on the website | |
2 This particular Popper quotation is also used as a definition of replication in Collins (1985).
3 In response to these cautions and to the sociological work by Collins, Medawar, and Latour, we chose to write this paper in a narrative style. In a paper specifically about the process of doing science we believe it is important to describe our process as accurately as possible.
4 The choice of how to simplify, what to foreground and what to background, is at the heart of the modeling process.
5 Though conceptual models usually take the form of written descriptions, they can take other forms. For instance, they could be diagrams, images, aural descriptions, or even pseudo-code. It should be noted that our definition of conceptual models includes both informal models, as well as non-executable formal models like UML diagrams or flowcharts.
6 It should be noted that it might be impossible to conclusively prove that two models are distributionally equivalent due to the problem of induction and the stochastic nature of these models.
7 The philosophical problems concerning the validity of replication mentioned above are not just theoretical, but are ubiquitous in the practice of replication.
8 This term comes from experimental social science. Another related term from measurement theory is reliability. A necessary condition for a model to be verified is that it is reliable. A reliable model is one the produces the same results over time. However, there are many dimensions to reliability, for a more complete discussion see Carmines and Zeller (1979).
9 Many distinct definitions of validation have been proposed by philosophers of science (seeKleindorfer et al. 1998), but the one given here should suffice for our discussions.
10 For additional examples of validation of agent-based models with real world data see Grimm et al.'s (2005) paper on pattern-oriented modeling.
11 A full discussion of validation is beyond the scope of this paper, but validation can occur either at the level of macro-results or micro-rules (Wilensky and Reisman 2006). In this case Wilensky was asking Rand to consider the validity of the micro-rules by comparing the models' micro-rules to those observed in reality.
12 By shuffled, we mean that the order of the list was rearranged randomly each time the list was iterated. By unshuffled, we mean that the order of the list was the same each time it was iterated.
13 We had a limited number of data points (10) for the Axelrod-Hammond model. The Wilensky-Rand model results bear out even when averaged over 100 runs.
14 This is a strategy that may have limited applicability. However, as ABM is still relatively young, the majority of original model implementers are still alive and accessible.
15 Grimm et al. (2006) have recently explored this issue with respect to ecological modeling.
16 As described in Table 4, Axelrod and Hammond made available a large amount of data on their website, including the full source code of the model and detailed accounts of experiments that they had run but not published. This far exceeds the average amount of information made publicly available by agent-based model authors. However, despite these efforts it still required a considerable amount of effort to perform this replication.
ARTHUR, W B (1994). Inductive Reasoning and Bounded Rationality. The American Economic Review 84(2): 406-411.
AXELROD, R (1986). An evolutionary approach to norms. The American Political Science Review, 80(4), 1095-1111.
AXELROD, R (1997a). "Advancing the Art of Simulation in the Social Sciences". In Conte R, Hegelsmann R and Terna P (Eds.) Simulating Social Phenomena, Berlin, Springer-Verlag: 21-40.
AXELROD, R (1997b). The Dissemination of Culture: A Model with Local Convergence and Global Polarization. The Journal of Conflict Resolution 41(2): 203-26.
AXELROD, R and Hammond, R A (2003). The Evolution of Ethnocentric Behavior. Paper presented at the Midwest Political Science Convention, Chicago, IL.
AXTELL, R, Axelrod, R, Epstein, J M and Cohen, M D (1996). Aligning Simulation Models: A Case Study and Results. Computational and Mathematical Organization Theory 1 123-141.
BELDING, T C (2000). Numerical Replication of Computer Simulations: Some Pitfalls and How To Avoid them, University of Michigan's Center for the Study of Complex Systems, Technical Report.
BIGBEE, G, Cioffi-Revilla, C and Luke, S (2005). Replication of Sugarscape using MASON. Paper presented at the European Social Simulation Association, Koblenz, Germany.
CARMINES, E G and Zeller, R A (1979). Reliability and Validity Assessment. London, Sage Publications.
CIOFFI-REVILLA, C and N Gotts (2003). Comparative analysis of agent-based social simulations: GeoSim and FEARLUS models. Journal of Artificial Societies and Social Simulation, 6(4)10 https://www.jasss.org/6/4/10.html.
COHEN, M, Axelrod, R and Riolo, R (1998). CAR Project: Replication of Eight "Social Science" Simulation Models, http://www.cscs.umich.edu/Software/CAR-replications.html.
COHEN, M D, March, J G and Olsen, J P (1972). A garbage can model of organizational choice. Administrative Science Quarterly, 17(1), 1-25.
COLLIER, N, Howe, T and North, M (2003). Onward and Upward: The Transition to Repast 2.0. Paper presented at the First Annual North American Association for Computational Social and Organizational Science Conference, Pittsburgh, PA.
COLLINS, H M (1985). Changing Order: Replication and Induction in Scientific Practice. London, SAGE Publications.
DENSMORE, O. (2004). Open Source Research, A Quiet Revolution. http://backspaces.net/research/opensource/OpenSourceResearch.html.
EDMONDS, B and Hales, D (2003). Replication, Replication and Replication: Some Hard Lessons from Model Alignment. Journal of Artificial Societies and Social Simulation 6(4)11 https://www.jasss.org/6/4/11.html.
EDMONDS, B and Hales, D (2005). Computational simulation as theoretical experiment. Journal of Mathematical Sociology, 29, 1-24.
EDWARDS, M, Huet, S, Goreaud, F and Deffuant, G (2003). Comparing an individual-based model of behaviour diffusion with its mean field aggregate approximation. Journal of Artificial Societies and Social Simulation, 6(4)9 https://www.jasss.org/6/4/9.html.
EPSTEIN, J and Axtell, R (1996). Growing Artificial Societies: Social Science from the Bottom Up. Cambridge, MA, MIT Press.
EPSTEIN, J (1999). Agent-based computational models and generative social science, Complexity 4(5): 41-60.
FOGEL, D B, Chellapilla, K and Angeline, P J (1999). Inductive Reasoning and Bounded Rationality Reconsidered. IEEE Transactions on Evolutionary Computation 3(2): 142-146.
FORRESTER, J W (1961). Industrial Dynamics. Cambridge, MA: MIT Press
GALAN, J M and Izquierdo, L R (2005). Appearances Can Be Deceiving: Lessons Learned Re-Implementing Axelrod's 'Evolutionary Approach to Norms'. Journal of Artificial Societies and Social Simulation 8(3)2 https://www.jasss.org/8/3/2.html.
GILES, J (2006). The trouble with replication. Nature 442(7101): 344-7.
GRIMM, V, Revilla, E et al. (2005). Pattern-Oriented Modeling of Agent-Based Complex Systems: Lessons from Ecology. Science 310: 987-991.
GRIMM, V, Berger, U, et al. (2006). A standard protocol for describing individual-based and agent-based models. Ecological Modelling 198: 115-126.
HALES, D, Rouchier, J and Edmonds, B (2003). Model-to-Model Analysis. Journal of Artificial Societies and Social Simulation 6(4)5 https://www.jasss.org/6/4/5.html.
HAMMOND, R A and Axelrod, R (2005a). Evolution of Contingent Altruism When Cooperation is Expensive. Theoretical Population Biology: In Press.
HAMMOND,, R A and Axelrod, R (2005b). The evolution of ethnocentrism, University of Michigan, Technical Report.
IZQUIERDO, L R, and Polhill, J G (2006). Is your model susceptible to floating point errors? Journal of Artificial Societies and Social Simulation, 9(4)4 https://www.jasss.org/9/4/4.html.
JANIS, I L (1982). Groupthink: psychological studies of policy decisions and fiascoes. Boston, Houghton Mifflin.
JONES, C (2000). Software assessments, benchmarks, and best practices. Boston, MA, Addison-Wesley Longman Publishing Co., Inc.
KLEINDORFER, G B, O'Neill, L and Ganeshan, R (1998). Validation in simulation: Various positions in the philosophy of science. Management Science, 44(8), 1087-1099.
LATOUR, B and Woolgar, S (1979). Laboratory Life: The Social Construction of Scientific Facts. Beverly Hills, Sage Publications.
LUKE, S, Cioffi-Revilla, C et al. (2004). MASON: A Multi-Agent Simulation Environment. Paper presented at the 2004 SwarmFest Workshop, Ann Arbor, MI.
MEDAWAR, P B (1991). The Threat and the Glory: Reflections on Science and Scientists. Oxford, Oxford University Press.
MOSS, S (2000). Canonical tasks, environments and models for social simulation. Computational and Mathematical Organization Theory, 6(3), 249-275.
NORTH, M J and Macal, C M (2002). The Beer Dock: Three and a Half Implementations of the Beer Distribution Game. Paper presented at Swarmfest.
PAPERT, S (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.
PARKER, M (2000). Ascape [computer software], The Brookings Institution.
POLHILL, J G, and Izquierdo, L R (2005). Lessons learned from converting the artificial stock market to interval arithmetic. Journal of Artificial Societies and Social Simulation, 8(2)2 https://www.jasss.org/8/2/2.html.
POLHILL, J G, Izquierdo, L R, and Gotts, N M (2005). The ghost in the model (and other effects of floating point arithmetic). Journal of Artificial Societies and Social Simulation, 8(1)5 https://www.jasss.org/8/1/5.html.
POLHILL, J G, Izquierdo, L R, & Gotts, N M (2006). What every agent-based modeller should know about floating point arithmetic. Environmental Modelling and Software, 21(3), 283-209.
POPPER, K R (1959). The Logic of Scientific Discovery. New York, Harper & Row.
ROUCHIER, J (2003). Re-implementation of a multi-agent model aimed at sustaining experimental economic research: The case of simulations with emerging speculation. Journal of Artificial Societies and Social Simulation 6(4)7 https://www.jasss.org/6/4/7.html.
TAYLOR, C A (1996). Defining Science: A Rhetoric of Demarcation. Madison, Wisconsin, The University of Wisconsin Press.
TISUE, S and Wilensky, U (2004). NetLogo: A simple environment for modeling complexity. Paper presented at the International Conference on Complex Systems (ICCS 2004), Boston, MA, May 16-21, 2004.
TONER, J, Yuhai, T and Sriram, R (2005) Hydrodynamics and phases of flocks, Annals of Physics 318(1):170-244.
WILENSKY, U (1999). NetLogo [computer software]. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
WILENSKY, U and Reisman, K (2006). Thinking like a wolf, a sheep or a firefly: Learning biology through constructing and testing computational theories. Cognition & Instruction, 24(2), 171-209.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]