Oswaldo Terán, Johanna Alvarez, Magdiel Ablan and Manuel Jaimes (2007)
Characterising Emergence of Landowners in a Forest Reserve
Journal of Artificial Societies and Social Simulation
vol. 10, no. 3 6
<https://www.jasss.org/10/3/6.html>
For information about citing this article, click here
Received: 15-Nov-2006 Accepted: 29-Mar-2007 Published: 30-Jun-2007
 Abstract
Abstract
|
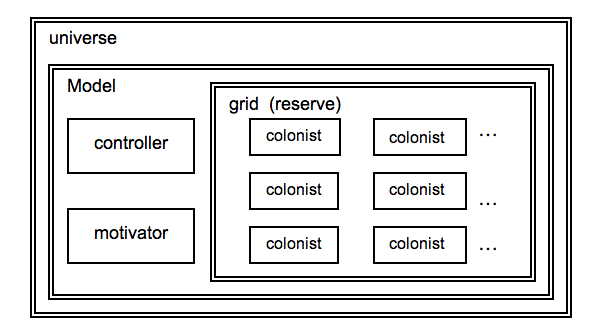
| Figure 1. Scheme of the Model (Agents and Landscape (grid)) |
[[imitateNeighbour 4] [selfReasoning 3] [followController 2] [followMotivator 1]],
(weight for imitating a neighbour)/(total sum of the weights) = 4/(4+3+2+1).The probabilities for the other alternatives are calculated in the same manner.
E(b, VectorLabels) = ∑val(labeli) ≥ 0 bval(labeli) - ∑ val(labeli) < 0 b|val(labeli)| (1)where:
vectorLabels = (imitateNeighbour, selfReasoning);and, the values of these labels are:
val(imitateNeighbour) = 4, val(selfReasoning) = 3.
E(1.2, (imitateNeighbour, selfReasoning)) = 1.24 + 1.23 = 3.8016Similarly, the other option: notToOccupy land would be evaluated. Then the choice is made, in accordance with the resulting endorsement values. In the present model, the option with the highest endorsement value is chosen by the agent. After each choice, the colonist adds a new label to the option taken; i.e., if the agent chooses toOccupy land through self-reasoning, then it adds the label selfReasoning to the option toOcuppy land.
1. Set up the simulation parameters (e.g., variables and instances of agents)
1.1 Model initialises the overall simulation model, the parameters and variables, e.g., initial number of colonists of each type; agent grid; agent colons; agent motivator; and agent controller. It also asks the user for parameters such as: size of a colonist's neighbourhood, percentage of colonists removed from the reserve each iteration time (year), total number of colonists at the beginning of the simulation, percentage of colonists of each type to set up initially, number of "new" colonists coming into the reserve each iteration time, number of simulation time steps (n) (years), etc. Colonists are located randomly in the grid (several runs were carried out for each parameter settings, showing consistent outputs). 1.2 Colonist sets up his endorsement scheme, according to his type. 1.3 Controller defines its policy (it always suggests not to occupy land).
1.4 Motivator defines its policy (it always suggests to occupy land). 1.5 Grid defines parameters for graphical output (e.g., size of each cell at the graphical output).
2. For year i (i = 1,2...n)
2.1 Model
2.1.1 It changes the status of land (after five years of occupation a piece of land (a cell) changes its status from "Agriculture" to "Cattle rising", indicating the loss of fertility over time).
2.1.2 If several colonists intend to occupy the same cell, Model selects randomly the colonist that finally will occupy such a cell.
2.1.3 New colonists are introduced into the reserve (according to the parameter given by the user).
2.1.4 A percentage of colonists are removed from the reserve. Colonists to be removed are chosen from those with low size of land holding — this resembles a bias observed in real life.
2.2 Colonist i (i = 1,2, ... , k)
2.2.1 Creates: a) a list of neighbour colonists, who are candidate to be imitated; and b) a list of non-occupied cells that are candidate to be taken over.
2.2.2 Selects a way for deciding about occupying land in accordance to his preferences (e.g., either imitating a neighbour, self-reasoning, listening to the controller, or listening to the motivator). In case of choosing self-reasoning, the colonist will make a choice in 2.2.3 using the endorsements scheme. In the other case, he will make a choice (in 2.2.3) following the suggestion of either a neighbour, the controller, or the motivator.
2.2.3. Using the selected way for deciding in 2.2.2., it chooses between the actions of "to occupy" or "not to occupy" land. If it chooses "to occupy" land, then it randomly selects one cell available from the region of land it holds, if there is a non-occupied available cell. If a cell has been chosen, the colonist sets a clause in Model indicating it intends to occupy such a cell — this is so because, in where case of more than one colonist intends to occupy the same cell, Model will randomly settle whoever takes over the cell. After choosing, the selected action (either toOccupy or notToOccupy) is endorsed with a label following the selected way for deciding (imitating a neighbour, self-reasoning, etc.) in 2.2.2. This label will determine a weight for the decision following the colonist's preference.
2.2.4 In the case the colonist decides to occupy land without available free land, it makes a bid to a neighbour directly accessible from the continuous region of land it holds, with a size of land holding smaller than its own, if any. The colonist prefers cells occupied for less than five years (or in the state "Agriculture").
2.2.5 If the colonist has land biddings, then it chooses to sell to that buyer with the largest size of land holding[3]. 2.2.6 If the colonist's size of land holding is zero, the colonist leaves the reserve in the case in which he has decided not to occupy land (see 2.2.3); otherwise, he will continue in the forest reserve trying to occupy the land next iteration time (year).
2.3 Controller
2.3.1 No action is performed (he keeps his suggestion continuously: notToOccupy land). One of his actions, to remove colonists, has been efficiently implemented in agent Model
2.4 Motivator
2.4.1 No action is performed (he keeps his suggestion continuously: toOccupy land)
2.5. Grid
2.5.1 Updates occupied points (i.e., relation: (cell point, occupying colonist))
2.5.2 Pictures the grid on the monitor (by sending a graphical output).
| Table 1: Simulation scenarios. Scenario 1 has two sub-scenarios: scenario 1(15) and scenario 1(30) representing scenario 1 observed at years 15 and 30, respectively. | |||||
| Variable Scenario | % colonists type 1 | % colonists type 2 | % colonists type 3 | % colonists removed / year | Year |
| 1(15) | 0.5 | 0.5 | 0.3 | 0.02 | 15 |
| 1(30) | 0.5 | 0.2 | 0.3 | 0.02 | 30 |
| 1 | 0.5 | 0.5 | 0.3 | 0.02 | 50 |
| 2 | 0.5 | 0.2 | 0.3 | 0.01 | 50 |
| 1 | 0.5 | 0.2 | 0.3 | 0.02 | 50 |
| 3 | 0.5 | 0.2 | 0.3 | 0.02 | 50 |
| 4 | 0.8 | 0.1 | 0.1 | 0.02 | 50 |
| 5 | 0.1 | 0.8 | 0.1 | 0.02 | 50 |
| 6 | 0.1 | 0.1 | 0.8 | 0.02 | 50 |
| (exponential:) Rank(SHL) = (Constant1) e-SHL | (2) |
| (power-law:) Rank(SHL)= (Constant2) * SHL-τ | (3) |
Taking the natural logarithm (Ln) at both sides of 1) and 2), we have the following linear relations:
| (exponential:) Ln(Rank(SHL)) = - SHL + Constant3 | (4) |
| (power-law:) Ln(Rank(SHL)) = -τ* Ln(SHL) + Constant4 | (5) |
These relations are analysed, for all simulation scenarios, by using regression analysis discussed in the following subsections. Although for each scenario several runs were performed, with consistent results, only one of them is shown below.
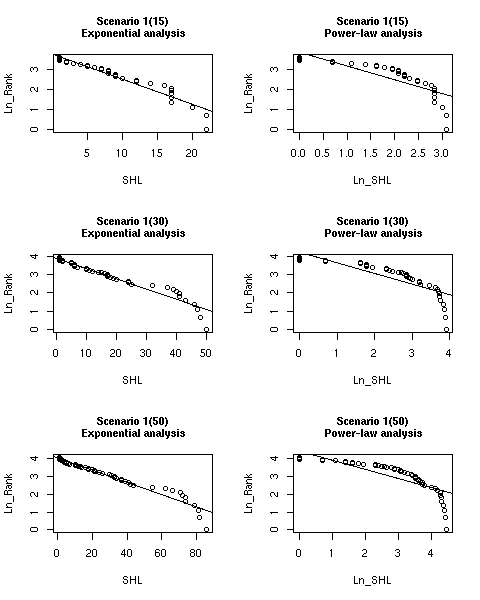
| Scenario 1(15), exponential-analysis Multiple R-Squared: 0.9237, p-value: < 2.2e-16 Slope: -0.12647 | Scenario 1(15), power-law-analysis Multiple R-Squared: 0.6913 p-value: 1.018e-10 Slope: -0.68672 |
| Scenario 1(30), exponential-analysis Multiple R-Squared: 0.937 p-value: < 2.2e-16 Slope: -0.055878 | Scenario 1(30), power-law-analysis Multiple R-Squared: 0.7191 p-value: 2.154e-15 Slope: -0.57752 |
| Scenario 1(50), exponential-analysis Multiple R-Squared: 0.9473 p-value: < 2.2e-16 Slope: -0.03386 | Scenario 1(50), power-law-analysis Multiple R-Squared: 0.683 p-value: 4.261e-16 Slope: -0.50766 |
| Figure 2. Statistics from the regression analysis for scenario 1 at different simulation times | |
|
| Figure 3. Regression lines vs. simulated data for scenario 1 at different times |
|
|
| Figure 4. Example of the Landscape at time t = 50 years |
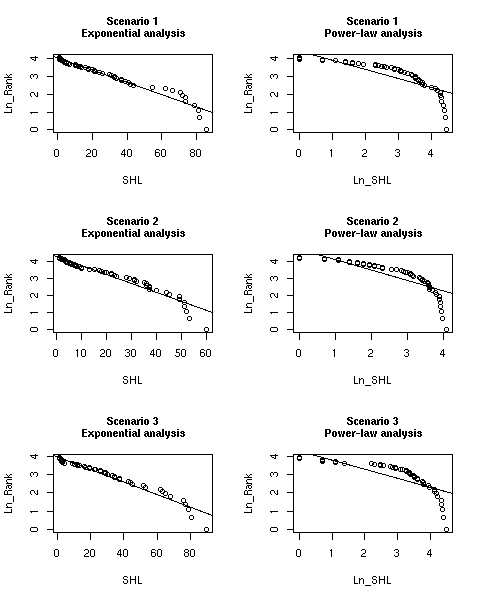
| Scenario 1, exponential-analysis Multiple R-Squared: 0.9473 p-value: < 2.2e-16 Slope: -0.03386 | Scenario 1, power-law-analysis Multiple R-Squared: 0.683 p-value: 4.261e-16 Slope: -0.50766 |
| Scenario 2, exponential-analysis Multiple R-Squared: 0.9419 p-value: < 2.2e-16 Slope: -0.052885 | Scenario 2, power-law-analysis Multiple R-Squared: 0.7061 p-value: < 2.2e-16 Slope: -0.6191 |
| Scenario 3, exponential-analysis Multiple R-Squared: 0.9535 p-value: < 2.2e-16 Slope: -0.033557 | Scenario 3, power-law-analysis Multiple R-Squared: 0.6549 p-value: 3.862e-13 Slope: -0.48432 |
| Figure 5. Statistics from the regression analysis for scenarios 1, 2, 3 | |
|
| Figure 6. Regression lines vs. simulated data for scenarios 1, 2, 3 |
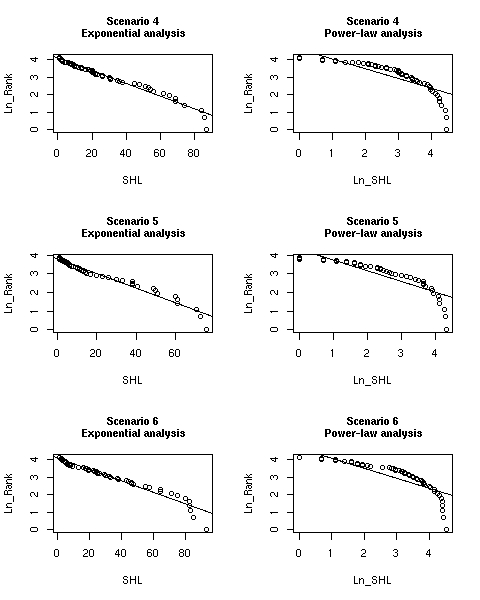
| Scenario 4, exponential-analysis Multiple R-Squared: 0.9709 p-value: < 2.2e-16 Slope: -0.0363740 | Scenario 4, power-law-analysis Multiple R-Squared: 0.72 p-value: < 2.2e-16 Slope: -0.55924 |
| Scenario 5, exponential-analysis Multiple R-Squared: 0.9578 p-value: < 2.2e-16 Slope: -0.038644 | Scenario 5, power-law-analysis Multiple R-Squared: 0.7604 p-value: 3.465e-16 Slope: -0.56933 |
| Scenario 6, exponential-analysis Multiple R-Squared: 0.9515 p-value: < 2.2e-16 Slope: -0.0324927 | Scenario 6, power-law-analysis Multiple R-Squared: 0.733 p-value: < 2.2e-16 Slope: -0.57004 |
| Figure 7. Statistics from the regression analysis for scenarios 4, 5, and 6. | |
|
| Figure 8. Regression lines vs. simulated data for scenarios 4, 5 and 6 |
| Table 2: Scenarios are based on scenario 1 as defined above. Factors f1-f3 are incrementally removed. | |||||
| Variable Scenario | Factors removed from the model | % colonists type 1 | % colonists type 2 | % colonists type 3 | Year |
| 1-NoF1 | f1 | 0,5 | 0,2 | 0,3 | 50 |
| 1-NoF1-2 | f1, f2 | 0,5 | 0,2 | 0,3 | 50 |
| 1-NoF1-2-3 | f1, f2, f3 | 0,5 | 0,2 | 0,3 | 50 |
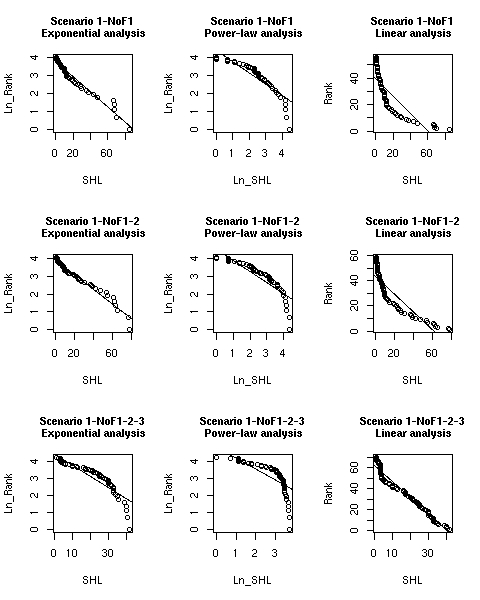
| Scenario 1-NoF1, exponential-analysis Multiple R-Squared: 0.9527 p-value: < 2.2e-16 Slope: -0.042346 | Scenario 1-NoF1, power-law-analysis Multiple R-Squared: 0.8239 p-value: < 2.2e-16 Slope: -0.63037 | Scenario 1-NoF1, linear-analysis Multiple R-Squared: 0.6862 p-value: 3.328e-15 Slope: -0.65379 |
| Scenario 1-NoF1-2, exponential-analysis Multiple R-Squared: 0.9649 p-value: < 2.2e-16 Slope: -0.040941 | Scenario 1-NoF1-2, power-law-analysis Multiple R-Squared: 0.7985 p-value: < 2.2e-16 Slope: -0.61396 | Scenario 1-NoF1-2, linear-analysis Multiple R-Squared: 0.7849 p-value: < 2.2e-16 Slope: -0.70489 |
| Scenario 1-NoF1-2-3, exponential-analysis Multiple R-Squared: 0.8466 p-value: < 2.2e-16 Slope: -0.063773 | Scenario 1-NoF1-2-3, power-law-analysis Multiple R-Squared: 0.6193 p-value: 6.659e-16 Slope: -0.63247 | Scenario 1-NoF1-2-3, linear-analysis Multiple R-Squared: 0.9676 p-value: < 2.2e-16 Slope: -1.52501 |
| Figure 9. Statistics from the regression analysis for scenarios 1-NoF1-2-3, 1-NoF1-2, 1-NoF1 | ||
| |
| Figure 10. Regression lines vs. simulated data for scenarios 1-NoF, 1-NoF1-2, 11-NoF1-2-3 | |
| Scenario 1-NoF1-3, exponential-analysis Multiple R-Squared: 0.9477 p-value: < 2.2e-16 | Scenario 1-NoF1-3, power-law-analysis Multiple R-Squared: 0.7048 p-value: < 2.2e-16 | Scenario 1-NoF1-3, linear-analysis Multiple R-Squared: 0.9092 p-value: < 2.2e-16 |
| Scenario 1-NoF2-3, exponential-analysis Multiple R-Squared: 0.7145 p-value: < 2.2e-16 | Scenario 1-NoF2-3, power-law-analysis Multiple R-Squared: 0.4383 p-value: 3.239e-10 | Scenario 1-NoF2-3, linear-analysis Multiple R-Squared: 0.973 p-value: < 2.2e-16 |
| Figure 11. Statistics from the regression analysis for scenarios 1-NoF1-3, 1-NoF2-3. | ||
| Table 3: Number of colonists within a given category of size of land holding. Source: Rojas, 1993 | |
| Land holding size (Ha) | Number of colonists |
| < 50 | 10 |
| 51 — 500 | 62 |
| 501 — 950 | 7 |
| 951 — 1400 | 2 |
| 1401 -1850 | 1 |
| > 1850 | 1 |
| Table 4: Summary of results of 5 runs of the validation procedure applied of real data. All the values are statistically highly significant (p < 0.001) | ||||
| Exponential | Power law | |||
| min | max | min | max | |
| R2 | 0.8206 | 0.9539 | 0.5615 | 0.7836 |
| slope | -2.66 x 10-3 | -2.06 x 10-3 | -0.56 | -0.77 |
2 At the CFR this process is somewhat different at present, as the forest has been almost totally removed. However, this process is taking place in other Venezuelan forest reserves.
3 Prospective sellers only have a choice: to sell land. In the future, in more detailed experiments, a seller will be able to choose whether or not to sell land. In the present model there is not price manipulation - we might say that the buyer with the highest amount of land, among the buyers, makes the highest bidding.
4 Latin-American culture is obviously different from European (Western) culture, being a sort of "marginal-western" culture. This is a consequence, in part, of the fact that "modern progress" has been more a "tale" and an excuse for exploiting natural resources (and people), while the conditions for a real Modern Progress have historically been neglected.
BERGER, T. 2001. Agent-based spatial models applied to agriculture: A simulation tool for technology diffusion, resource use changes, and policy analysis. Agricultural Economics 25 (2-3): 245-260
CENTENO J., C., 1997. Deforestation Out of Control in Venezuela. http://www.ciens.ula.ve/~jcenteno/DEFOR-EN.html (Spanish version available at:http://www.ciens.ula.ve/~jcenteno/DEFOR-ES.html)
CESIMO, Gaia, 1998, Caso Venezuela: Deforestación y Políticas de la Propiedad de la Tierra en la Reserva Forestal de Caparo (A Multi-Media Tool for Natural Resources Management and Environment Education). Centro de Simulación y Modelos de la Universidad de los Andes, Mérida, Venezuela. http://cesimo.ing.ula.ve/GAIA/CASES/VEN
COHEN P., 1985, Heuristic Reasoning: An Artificial Intelligence Approach, Pitman Advanced Publishing Program, Boston.
CONTE Rosaria, and Paolucci Mario (2001), Intelligent Social Learning, Journal of Artificial Societies and Social Simulation, 4(1)3, https://www.jasss.org/4/1/3.html (Spanish version available at: http://www.universidad-de-la-calle.com/Aprendizaje_social.html)
CYERT R., and March J., 1992 [1963], A behavioral Theory of the Firm, 2nd edition. Blackwell Publishers, Cambridge, MA.
EDMONDS B. and Hales D., 2004, When and Why Does Haggling Occur? -Some suggestions from a qualitative but computational simulation of negotiation, Journal of Artificial Societies and Social Simulation vol. 7, no. 2, https://www.jasss.org/7/2/9.html.
GOTTS Nicholas, and Dawn Parker, 2004a, Modelling Size Distributions of Rural Land Holding in Scotland, Proceeding of the Second International Conference of the European Social Simulation Association ESSA' 04 and Model to Model Workshop, September 16-19, Valladolid, Spain.
GOTTS Nicholas, and Dawn Parker, 2004b, Size Distributions of Land Holding in an Agent-Based Model of Rural Land Use, Proceedings of The Agent 2004 Conference on Social Dynamics, Reflexivity and Emergence, Oct. 7-9, Chicago, IL.,USA. http://agent2004.anl.gov/agenda2004.html.
HAPPE, K., K. Kellermann, and A. Balmann. 2006. Agent-based Analysis of Agricultural Policies: an Illustration of the Agricultural Policy Simulator AgriPoliS, its Adaptation and Behavior. Ecology and Society 11(1): 49. http://www.ecologyandsociety.org/vol11/iss1/art49
JAIMES M., 2004, Una representación del proceso de ocupación y uso de la tierra de la Reserva Forestal de Caparo, Undergraduate Thesis, Universidad de los Andes. Venezuela.
NEWELL A., 1990, Unified Theories of Cognition, Harvard University Press, Cambridge, MA, USA.
MORENO N., Quintero R., Ablan M., Barros R., Dávila J., Ramírez H., Tonella G. and Acevedo M. 2007. Biocomplexity of deforestation in the Caparo tropical forest reserve in Venezuela: An integrated multi-agent and cellular automata model. Environmental Modelling and Software, 22(5) pp. 664-673
MOSS S., 1995, Control Metaphors in the Modelling of Decision-Making Behaviour, Computational Economics, v.8, pp. 283-301
MOSS S, Gaylard H, Wallis S, and Edmonds B, 1998, SDML: A Multi-Agent Language for Organizational Modelling, Computational Mathematical Organization Theory, 4(1), pp. 43-69.
MOSS, S, Edmonds B, and Wallis S, 1997, Validation and Verification of Computational Models with Multiple Cognitive Agents, CPM-97-25 http://www.cpm.mmu.ac.uk/cpmrep25.html.
MOSS S., Edmonds B. and Wallis S., 2000, The Power Law and Critical Density in Large Multi-Agent Systems, CPM Report Number 00-71, Manchester Metropolitan University, UK http://www.cpm.mmu.ac.uk/cpmrep71.html.
MOSS S., 2001, Game Theory: Limitations and an Alternative, Centre for Policy Modelling Report No. 01-80 http://cfpm.org/cpmrep80.html.
POLHILL, J. G., D. C. Parker, and N. M. Gotts. 2005. Introducing Land Markets to an Agent Based Model of Land Use Change: A Design. Third ESSA Conference, Koblenz, Germany, September 5-9, 2005
ROJAS López, J., 1993. La colonización agraria de las Reservas Forestales: ¿un proceso sin solución? Universidad de los Andes, Instituto de Geografía, Mérida, Venezuela. Cuadernos Geográficos No. 10, Junio de 1993.
SÁNCHEZ M., 1989, Situación Actual del Proceso de Ocupación de la Reserva Forestal en Caparo, Universidad de los Andes, Instituto de Geografía y Conservación de Recursos Naturales, Mérida, Venezuela.
SIMON H., 1946, The Proverbs of Administration, Reproduced in Shafritz et al., 1997.
SIMON H., 1984, The Sciences of the Artificial, MIT Press, Cambridge, Mass., USA.
TERÁN O, Alvarez J., Jaimes M. and Ablan M., 2005, "Land Occupation and Land Use Change in a Forest Reserve: A MABS Approach", Proceeding of the CABM-HEMA-SMAGET Joint International Conference on Multi-Agent Modelling for Environment Management, Bourg Saint Maurice-Les Arcs, France, March 21-25.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]