Jean-Philippe Cointet and Camille Roth (2007)

How Realistic Should Knowledge Diffusion Models Be?

Journal of Artificial Societies and Social Simulation vol. 10, no. 3 5
<https://www.jasss.org/10/3/5.html>

For information about citing this article, click here

Received: 13-Nov-2006    Accepted: 21-Apr-2007    Published: 30-Jun-2007

Abstract

Knowledge diffusion models typically involve two main features: an underlying social network topology on one side, and a particular design of interaction rules driving knowledge transmission on the other side. Acknowledging the need for realistic topologies and adoption behaviors backed by empirical measurements, it becomes unclear how accurately existing models render real-world phenomena: if indeed both topology and transmission mechanisms have a key impact on these phenomena, to which extent does the use of more or less stylized assumptions affect modeling results? In order to evaluate various classical topologies and mechanisms, we push the comparison to more empirical benchmarks: real-world network structures and empirically measured mechanisms. Special attention is paid to appraising the discrepancy between diffusion phenomena (i) on some real network topologies vs. various kinds of scale-free networks, and (ii) using an empirically-measured transmission mechanism, compared with canonical appropriate models such as threshold models. We find very sensible differences between the more realistic settings and their traditional stylized counterparts. On the whole, our point is thus also epistemological by insisting that models should be tested against simulation-based empirical benchmarks.

Keywords:

Agent-Based Simulation, Complex Systems, Empirical Calibration and Validation, Knowledge Diffusion, Model Comparison, Social Networks

Outline

1.1

Although the issue of knowledge diffusion has usually been appraised from a theoretical viewpoint, it stands, above all, for an empirical challenge. Real-world features, yet, are often represented by stylized hypotheses, while it is unclear how much diffusion dynamics may be affected by such assumptions. After first recalling the context and literature on knowledge diffusion models in Section 2, we thus introduce a simulation framework in Section 3 in order to evaluate the accuracy of various classical topologies and mechanisms. In other words, we push the comparison to more empirical benchmarks: real-world network structures and empirically measured mechanisms. We therefore carry a two-step analysis: in Section 4, we contrast diffusion dynamics between two real networks and several traditional topologies, notably scale-free graphs; in Section 5, we address interaction rules and compare an empirically-backed transmission mechanism with its stylized counterparts, such as threshold or cascade models.

Context and rationale

2.1

Models of knowledge diffusion within social networks have known an increased interest in the recent years, together with various kinds of studies on interaction networks. Initially, research on knowledge diffusion had been principally addressed by social scientists, both in sociology as well as, to a lesser extent, economics and organization & management sciences (Coleman et al. 1957; Rogers 2003). Authors in these fields have long had a qualitative approach, supported by ethnographic studies endeavoring at exhibiting mechanisms determinant of knowledge transmission and adoption behaviors (Robertson 1967; Rogers 1976; Granovetter 1987; Burt 1987; Valente 1995). In this area, quantitative models are eventually qualitative in their interpretation, as they are essentially featuring normative models within formerly acknowledged theoretical frameworks (Ellison and Fudenberg 1995; Abrahamson and Rosenkopf 1997; Deroian 2002).

2.2

As knowledge diffusion phenomena are conditioned by the intricate combination of agent behavior and structural effects, it progressively became apparent that it is crucial to correctly design and understand the effect of underlying network structures. This happened initially, still, on normative grounds, i.e. with stylized network structures (Morris 2000; Cowan and Jonard 2004; Keeling and Eames 2005), while an earlier emphasis by Rogers (1976) on empirical data had remained a longer term aim:

For network analysis to fulfill its potential, however, I feel we must improve the methods of data gathering and measurement (…). Longitudinal panel designs for networks analysis of diffusion process are also needed; along with field experiments, they help secure the necessary data to illuminate the over-time process of diffusion. (Rogers 1976)

2.3

Such empirical insight was additionally encouraged by recent findings from formal and natural sciences (particularly statistical physics and computer science) concerning several kinds of real-world networks, including social networks, and highlighting a series of notable topological features, such as power-law ("scale-free") degree distributions, high clustering, short network diameter (Watts and Strogatz 1998; Barabasi and Albert 1999, inter alia). Authors from these fields in turn started to investigate diffusion phenomena from a rather formal viewpoint: adopting a biological perspective first, building upon the epidemiological literature (Anderson and May 1979; Pastor-Satorras and Vespignani 2001; Lloyd and May 2001; Keeling and Eames 2005); then addressing topics increasingly related to social science, for instance rumor and behavior diffusion models (Newman 2002), thereby shedding light on both traditional issues, such as the extent of knowledge diffusion, and on more novel issues, such as, inter alia, effects of extremist fractions (Deffuant et al. 2002) or spread maximization (Kempe et al. 2003).

2.4

However, even if some authors insisted on the need for realistic topologies and diffusion behaviors backed by empirical measurements (Valente 1996; Wu et al. 2004; Leskovec et al. 2006), it is unclear how accurately present models and corresponding analytic solutions or simulations render real-world phenomena. If indeed both topology and transmission mechanisms have a key impact on these phenomena, to which extent does the use of more or less stylized assumptions affect modeling results?

2.5

First, network topology is often based on common social network morphogenesis models. Erdös and Rényi (1959) random graphs (ER) have long been a convincing reference (Barbour and Mollison 1990; Wasserman and Faust 1994; Zegura et al. 1996), while simpler settings use complete graphs or grid-based networks (Ellison and Fudenberg 1995; Deroian 2002). Small-world models (Watts and Strogatz 1998) have also occasionally been considered (Cowan and Jonard 2004), as well as less typical models, for instance featuring a central core everyone is connected to (Bala and Goyal 1998), or algebraically-constrained networks (Morris 2000). These models seemed rather less realistic when, as mentioned above, social networks among others were discovered to be "scale-free" — i.e. their connectivity distribution follows a power-law, which earlier models could not render. In the wake of a key result by Pastor-Satorras and Vespignani (2001) suggesting that such networks have radically distinct epidemiologic properties from those of ER networks^[1], in more recent diffusion models, scale-free networks are hence often considered (Delgado 2002; Amblard and Deffuant 2004; Ganesh et al. 2005; Crépey et al. 2006). On the other hand, to our knowledge, cultural diffusion models has scarcely been effectively simulated on real social networks^[2], while such approach obviously guarantees that all structural features of a real-world social network are present^[3]. Such networks, additionally, are already widely available (Barabási and Albert 1999 ; Robins and Alexander 2004; Wu et al. 2004; Kossinets and Watts 2006).

2.6

Second, knowledge diffusion mechanisms, even if plausible, are often lacking empirical support; as Leskovec, Adamic and Huberman (2006) put it, "[while former] models address the question of maximizing the spread of influence in a network, they are based on assumed rather than measured influence effects." A wide variety of behaviors can be postulated, from pay-off based models, common in economics (Ellison and Fudenberg 1995; Morris 2000), to explicitly knowledge-based models, based in particular on opinions vectors, continuous or discrete, one-dimensional (Axelrod 1997; Deroian 2002; Deffuant et al. 2002) or n-dimensional (Gilbert et al. 2001; Cowan and Jonard 2004; Klemm et al. 2005), revised and updated according to diverse mechanisms. Yet, while such hypotheses yield enlightening models and stylized facts, it is unclear to what extent realistic classes of knowledge diffusion mechanisms could yield different classes of models and model behaviors. In this respect, projects such as that of Valente (1996) seem to be isolated.

2.7

In line with recent efforts at appraising the role of various topologies (Amblard and Deffuant 2004; Ganesh et al. 2005; Crépey et al. 2006) and distinct mechanisms (Deffuant 2006), the aim of this paper is thus to push the comparison to more realistic benchmarks: real-world network structures and empirically measured propagation mechanisms. As we lack empirical data appraising at the same time knowledge transmission behaviors and underlying social network topology, we have to restrain our analysis to issues pertaining to topology on one side and, separately, to transmission rules on the other side. More precisely, we will appraise the discrepancy between stylized (in particular scale-free) networks and real-world networks (Section 4) and between stylized (in particular threshold) knowledge transmission models and realistic mechanisms (Section 5).

Simulation framework

Agents and information

3.1

We consider a set of N agents and a single piece of information which each agent may know of, or not. In other words, at any time t, the cultural state of the system can be described by a vector c(t) ∈ {0,1}^N, such that c_i(t)=1 if the i-th agent knows the piece of information at t, otherwise c_i(t)=0.

3.2

We assume knowledge acquisition to be strictly growing: agents acquiring the piece of information cannot lose it afterwards. In epidemiological terms, this is close to a "SI" model (Hethcote 2000). Formally, this means that c is a growing function of time: t ≤ t2 ⇒ c(t) ≤ c(t2).

Simulations

3.3

The initial setting is such that a given proportion λ of agents are initially "informed" (i.e. λN agents), while others are "ignorant" (i.e. (1 – λ)N).

3.4

Our discrete time simulation features knowledge exchange between agents interacting with each other. At each time step one interaction occurs, possibly leading to transmission of knowledge:

• Interaction occurring between pairs of agents chosen in the following way: a target agent i is chosen randomly among the population, then one of his neighbors j is randomly selected.
• Transmission if the chosen neighbor j is informed (i.e. c_j(t)=1), target agent knowledge is updated according to an information adoption rule to be specified below.

The algorithm is shown below in pseudo-code.

SET number_of_nodes := number of agents SET neighbor := ARRAY OF LISTS of size number_of_nodes SET state := ARRAY OF BOOLEANS ("INFORMED"/"NOT_INFORMED") of size number_of_nodes SET number_of_interactions := ARRAY OF INTEGERS of size number_of_nodes INITIALIZE neighbor[i] with the neighbor list for node i INITIALIZE state WITH "INFORMED" on a random selection of elements of size Integer_Part_Of(number_of_nodes*lambda) INTIIALIZE number_of_interactions WITH 0 on the whole array FOR each step of the simulation CHOOSE RANDOMLY an agent i IF state[i] IS "NOT_INFORMED" THEN CHOOSE RANDOMLY an agent j among neighbor[i] IF state[j] IS "INFORMED" THEN IF a uniform random variable in [[0, 1]] IS BELOW Probability_Of_Adoption_After_N_Interactions(number_of_interactions[i]) THEN state(i) := "INFORMED" END IF INCREMENT number_of_interactions(i) END IF END IF END FOR

Algorithm

3.5

This kind of simple protocol belongs to the wider family of gossip-based models (see Kempe and Kleinberg (2002), for instance). In a descriptive rather than normative perspective, we therefore consider that the social network represents past acquaintances which potentially induce future interactions, rather than being a permanent interaction network, where individuals are concurrently subject to the influence of all their neighbors. While this later approach is indeed more plausible for computer or neuron networks, epidemiology in the broad sense calls for more asynchronous models, where interactions between agents are the basic unit of study. As such, we take the social network as a static framework wherein social interactions take place in a dynamic setting: for any given period, actual dyadic interactions are chosen within the set of links composing the wider social network.

3.6

We measure the ratio of informed agents ρ among the whole population over time, ρ(t)=[1/N] ∑_i=1^N c_i(t), while using a totally random initial spread of informed agents (only ρ(0) = λ). Even if richer patterns could be thought of (such as e.g. infection time as a function of the distance, density of infected nodes) and richer initial conditions could also affect results (a particular choice of informed nodes consisting of, e.g., so-called superspreaders) (Crépey et al. 2006; Deffuant 2006), this part of the protocol remains extremely simple so that effects are both easily comparable across other conditions as well as already yielding very contrasted results.

Effect of the topology

4.1

We first discuss dynamics of information acquisition by focusing on topology. We use several network topologies produced by a gradual impoverishment of two original real networks as explained below.

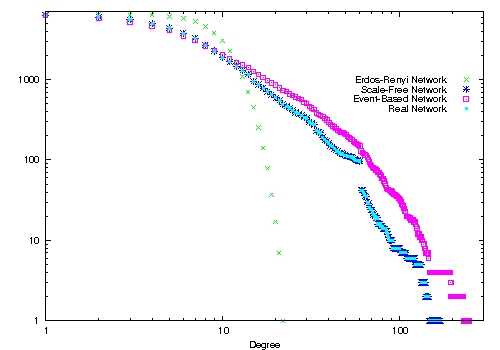
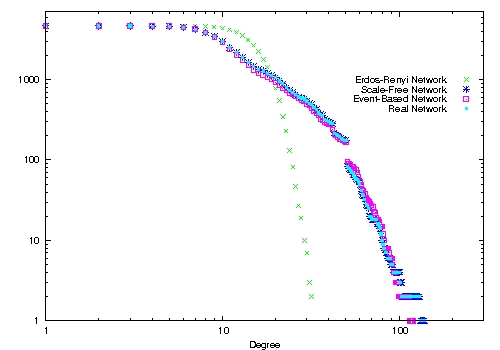
Figure 1. Cumulated degree distributions for the various network structures, using the Medline-base collaboration network (left) and the board interlock network (right). x-axis: degree k, y-axis: N(k)=∑ k' ≥ kN(k').

Empirical real networks

4.2

We use two real networks. The first one comes from a scientific collaboration network: nodes are authors and links represent coauthorship. We use data from the "Medline" bibliographical database^[4] for embryologists working on the model-animal zebrafish and consider articles mentioning "zebrafish" in their title or abstract (the field is such that authors working on this topic are unlikely not to mention it at least in the abstract) over years 2000-2004. We consider only the largest connected component. It is made of 6453 agents and 67392 undirected links, from a database of 2476 publications. The second network features directors jointly attending boards of major US firms or public institutions: nodes are directors and links are co-attendance relationships. This board interlock data comes from the website "Theyrule"^[5]. The largest connect component of this network is made of 4656 nodes and 76600 undirected links from a database of 510 corporate boards. Their degree distributions, shown on Figure 1, exhibit a power-law tail with a flatter head, typical of collaboration networks (Barabási and Albert 1999; Newman and Park 2003; Guimera et al. 2005) and several other social networks (Boguna et al. 2004; Holme et al. 2004; Kossinets and Watts 2006). While this kind of connectivity is often called "scale-free" or "power-law" in the literature, it may also accurately be fitted and described as "broad scale", "stretched-exponential", "log-normal" or "q-exponential" (Amaral et al. 2000; Redner 2005; White et al. 2006) on finite networks.

Topologies

4.3

Starting from the original empirical network, we investigate several network topologies created by progressively degenerating the original structure, i.e. by keeping less and less topogical features:

• Real Network (RN) The real network is either the original scientific collaboration network or board interlock network (respectively RN1 and RN2).
• Scale-Free (SF) The so-called "scale-free" networks (SF1 and SF2) are built from the original real networks (RN1 and RN2) by reshuffling links while preserving the original degree distribution (Molloy and Reed 1995). Total numbers of agents N and links M are also identical to those of the corresponding real networks, so original density d=M/N(N – 1) is also preserved for both networks.
• Erdös-Rényi (ER) These are ER random graphs (Erdös and Rényi 1959) (ER1 and ER2) that only preserve the original RN densities, using the same number of nodes N. Contrarily to SF and RN, the resulting degree distribution can be approximated by a Poisson law (Bollobás 1985), as shown on Figure 1.
• Complete Network (CN) The complete networks (CN1 and CN2) only share the number of agents N with the respective real networks (respectively RN1 and RN2). In contrast to other topologies, each agent is connected to all other agents, the total number of links is thus N(N – 1)/2.

Clustering structure

4.4

Apart from degree distributions, the clustering structure is of particular interest; some authors suggest it might significantly alter information diffusion (Bala and Goyal 1998). The usual definition of "clustering" relies on the proportion of transitive triples, or "friends who are also friends of friends." It may be defined by averaging the proportion of neighbors of node i who are also connected together:

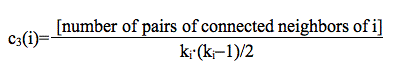
(1)

with k_i the degree of node i. Empirical social networks are known to exhibit an abnormally high average clustering coefficient ‹c₃›, compared to those found in SF and ER random networks (Newman and Park 2003); many models traditionally try to rebuild this statistical parameter as well. Our real networks do not derogate from this rule. RN1 exhibits a high ‹c₃› of .827, while SF1 only has a ‹c₃› of .00539. We observe the same discrepancy in the second network: clustering in RN2 is high (‹c₃› = .889) while it is two orders of magnitude smaller in SF2 (‹c₃› = .00395).

4.5

In an attempt to reconstruct a network topology that preserves both degree distribution and high ‹c₃›, we consider a last network model mimicking the original event-based structure (i.e. its collaboration or co-appearance structure):

• Event-Based We introduce a bipartite graph featuring agents on one side, events on the other side, and first assign to each agent and respectively to each event a "degree" drawn from empirical degree distributions. Put differently, the bipartite graph preserves the empirical distributions of agents per event and of events per agent — it maintains the original number of events featuring a certain number of agents, and reciprocally. Then, we link agents to events randomly, respecting their respective degrees. Finally, we compute the projection of this graph onto agents to build the collaboration network: two agents are linked when they participate in the same event.

4.6

The EB model yields networks which are closer to RN than SF in the sense that they keep more topological features:

1. We conserve the degree distribution, like in the SF case: the projection of a bipartite graph, whose distribution from agents to events exhibits a given power-law tail (as it does here) exhibits the same power-law tail (same exponent of the power law) (Guillaume and Latapy 2004).
2. We also conserve the clustering structure, unlike in the SF case: indeed, the clustering coefficient of the projection is high because of the clique-addition process precisely due to the projection; put simply, it is due to the joint involvement in common events — the empirical networks come from collaborations or participations in a common board, which implies cliques and thus more triangles (Newman et al. 2001; Guillaume and Latapy 2004).

Empirically, EB rebuilds fairly well both the degree distribution and the ‹c₃‹ clustering structure, with the same number of nodes and thus roughly the same number of links — see Figure 1 and Table 1.

4.7

A finer clustering structure has more recently been introduced, which relies on the proportion of transitive diamonds, or "friends of friends who are also friends of other friends." This "diamond coefficient" may be defined as the average proportion of common neighbors among the neighbors of a node i (Lind et al. 2005):

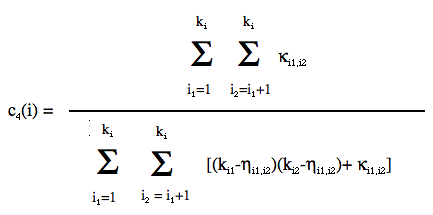
(2)

where κ_j1,j2 is the number of nodes which the j₁-th & j₂-th neighbors of i have in common (leaving out i) and η_j1,j2 = 1 + κ_j1,j2 + θ_j1,j2 where θ_j1,j2 = 1 if j₁ and j₂ are connected, 0 otherwise. EB1 acceptably approaches the ‹c₃› of RN1, but falls short of one order of magnitude for c₄ , suggesting that even an event-based reconstruction still misses part of the community structure of RN1. On the other hand, EB2 yields a ‹c₄› of .268 which is closer to the ‹c₄› of .398 for RN2. Values for these statistical parameters are gathered on Table 1.

4.8

Other topological features could also have been explored -such as path lengths (Zegura et al. 1996), mutuality (Newman 2003), cycles (White et al. 2006), inter alia — yet this selection of basic features will already provide significant discrepancies in the results between realistic settings and traditional models, acting as a convincing counter-example of the adequacy of the latter to mimick the former, even for our selection of statistical parameters.

4.9

To summarize, for each of our two real networks, we considered five distinct topologies: (i) real network RN, (ii) event-based network EB, (iii) scale-free network SF, (iv) Erdös-Rényi random graph ER, (v) complete network CN.

Table 1: Main characteristics of the various network structures derived from the real networks RN1 and RN2 in terms of: number of agents N, number links M, density d, degree distribution shape and clustering coefficients ‹c3› & ‹c4‹ (averaged quantities over 1000 networks for SF, ER & EB).
	RN1	SF1	ER1	CN1	EB1
N	6453
M	6.74104			2.08107	7.62104
d	.00162			1	.00183
degree dist.	power-law tail	Poisson	-	power-law tail
‹c3›	.827	.00539	.00199	1	.753
‹c4›	.400	.000260	.000158	1	.0694

	RN2	SF2	ER2	CN2	EB2
N	4656
M	7.66·104			2.17·107	7.68·104
d	.0035			1	.0035
degree dist.	power-law tail	Poisson	-	power-law tail
‹c3›	.889	.00395	.00403	1	.897
‹c4›	.398	.000261	.000217	1	.268

Simulation

4.10

As we focus on topology, we consider here the simplest interaction rule possible: the target agent automatically acquires the piece of information when his interlocutor already has it. A set of one thousand random instances of each kind of network is created (excepted for real and complete networks which are naturally unique). For each instance, we only work with the largest connected component, which is never made of less than 99.9% of the nodes (i.e. in the worst case, a negligible number of nodes is disconnected and left out). We then cast randomly the fraction λ of initially informed nodes over this giant component, and start the simulation. With connected networks, as is the case, the final asymptotic state of the system is obviously ρ(∞)=1. We are thus essentially interested in the shape and speed of convergence to that final state.

4.11

On Figure 2 is plotted the temporal evolution of ρ for each network topology (averaged over simulations on 1000 random instances). We observe that the dynamics are pretty similar when comparing the two original networks. The closer we are from the real network, the slower the dynamics — CN performs the fastest, RN the slowest. More precisely and most surprisingly, ER and SF networks seem to behave identically by showing extremely similar convergence shapes. On the contrary, the behavior of EB is slower than other topologies, even being the best approximation of RN, although with contrasted results: while EB2 provides a satisfactory reconstruction of the diffusion dynamics on RN2, the reconstruction offered by EB1 still diverges significantly from the behavior of RN1.

4.12

Our results are qualitatively only marginally sensitive to the initial proportion of informed nodes λ even if, the smaller λ, the slower the dynamics (see Figure 2-inset for λ = .002 vs. λ = .02). Hierarchy in convergence speed is independent of λ: CN always performs fastest, followed by ER and SF, then EB, and finally RN. Asymptotically, when λ goes to 1 all dynamics become similar.

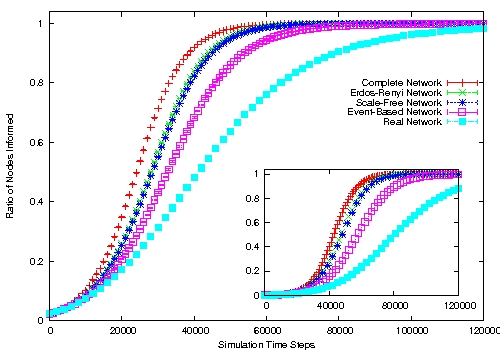
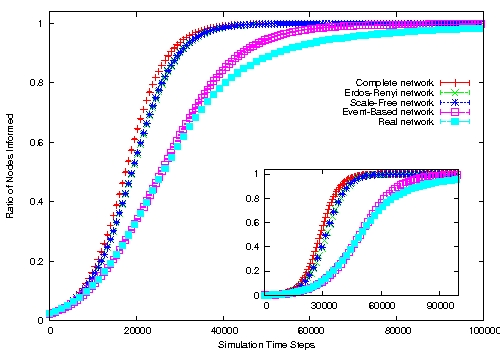
Figure 2. Simulation results for complete, Erdös-Rényi, Scale-Free, Event-Based and real networks, using λ = 0.02 (outset) and λ = 0.002 (inset), along with associated 99% confidence intervals. Topologies built from the scientific collaboration network (left) and the board interlock network (right).

Degree distribution, clustering structure, and real networks

4.13

As such, diffusion on RN is slower than on any other topology studied here. This may be due to its complex underlying community structure, consistently with common claim in innovation studies that when agents are likely to interact more with agents they know and less with "remote" agents, it is less beneficial to knowledge propagation (Granovetter 1973 ; Bala and Goyal 1998) — denser clusters arguably provide more redundancies in the distribution of information among neighbors. More to the point, as Granovetter (1973) puts it, "if one tells a rumor to all his close friends, and they do likewise, many will hear the rumor a second and third time, since those linked by strong ties tend to share friends." A previous study by Bala and Goyal (1998) argued that overlapping neighborhoods tend to make the diffusion of innovation slower, Eguiluz and Klemm (2002) later noted that epidemic threshold in highly clustered scale-free networks exhibited differences with the result for randomly wired networks.

4.14

This might explain why we get slower diffusion with EB than with SF, and even slower diffusion with RN in general, whose alleged community structure — plausibly constrained by paradigmatic fields, communities of practice, etc. — could not be perfectly reproduced. However, ‹c₄› values seem to provide a good assessment of the quality of this community structure reconstruction: when ‹c₄› is one order of magnitude smaller in EB1 than in RN1, diffusion speed is indeed significantly different; whereas when ‹c₄› is comparable, like in EB2 and RN2, diffusion speed too is comparable.

4.15

While it is likely that "the SF nature cannot be neglected in the practical estimates of epidemic and immunization thresholds in real networks" (Pastor-Satorras and Vespignani 2002), it may well be far from sufficient: not all SF networks are equal (May and Lloyd 2001; Boguna and Pastor-Satorras 2002; Eguiluz and Klemm 2002) and, here, the most random SF network actually displays a behavior more similar to ER than to RN — even if, for some other models, there may be a more or less sensible behavioral difference between SF and ER (Dorogovtsev and Mendes 2003; Barthélémy et al. 2005), under our protocol they are negligible compared to RN. In contrast and in particular, EB results suggest a special influence of community structure in general (Szendröi and Csányi 2004).

Concluding remarks

4.16

The jury may thus be still out as to indicate which topological features should absolutely be reconstructed for an artificial network to behave realistically with respect to some phenomena. Meanwhile, when possible, it could be safer to make an extensive usage of real network topologies when developing diffusion models. This attitude implies a pre-eminent role for simulations: if one needs analytical results on a given diffusion phenomenon, thereby requiring a theoretical social network model, one should check first that simulations provide matching behaviors on a real social network — or several ones, as it may also be interesting to compare how different diffusion dynamics behave on various empirical networks.

Effect of transmission rules

5.1

The protocol we presented in the previous section, where any interaction entails information transmission, is simple yet wholly arbitrary. In this section, we investigate transmission rules: as mentioned in the introduction, many varied knowledge transmission processes have been proposed in the literature. In the case of discrete information propagation, in particular, the "threshold model" — agents adopt knowledge if a given number or fraction of their neighbors already have — is a widespread reference (Granovetter 1987; Valente 1995; Valente 1996; Abrahamson and Rosenkopf 1997; Lew 2000; Gruhl et al. 2004), while the "cascade model" is also commonly used — agents have a given probability of adopting after interacting with already-informed neighbors (Goldenberg et al. 2001; Kempe et al. 2003).

5.2

Thus, and more broadly, we wish to appraise the success of some of these traditional models in approaching empirically-measured behavior — as we have seen, real networks may behave quite differently than classical scale-free networks: now, how much canonical models may now deviate from empirical phenomena? How realistic, then, should diffusion mechanisms be? In a fashion similar to what we did for the topology, we start with real-world data and consider various "degenerate" knowledge adoption behaviors which rely on canonical models. The model parameters will be chosen as best approximations of empirically observed behavior. We use RN as the underlying social structure.

Empirical influence mechanism

5.3

To design our original "empirical-based" transmission mechanism, we use empirical data extracted from a case study by (Leskovec et al. 2006), in which the propagation of a buying behavior is described — recommendations for acquiring DVDs are transmitted over an e-mail-based social network, and could be followed or not. Rather than focusing on this precise case study and its particular context, we use this data as an empirical illustration of the shape of one adoption behavior, among others.

5.4

This empirical data features the probability of adopting a recommendation after a certain number of received recommendations, that is, it is a final observation. More precisely, we know the probability P(n) of having bought some item given that n recommending interactions for this item have occurred (see Figure 3). Assuming that this process is the final outcome of a series of interactions where adoption was possible and probable after each interaction, we may deduce the adoption probability for each particular interaction. In other words, we can deduce the probability of adoption exactly at the n-th recommending interaction, given that there have already been n – 1 recommending interactions. We call this probability p(n), which is precisely of interest for interaction-by-interaction models such as those we are working with here.

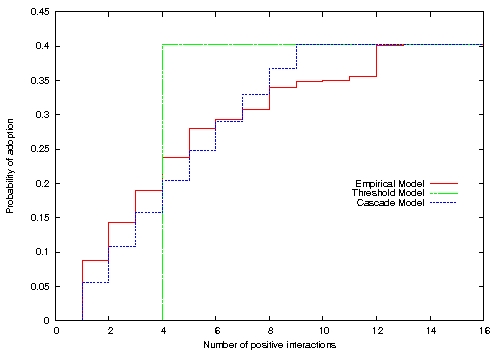
Figure 3. Final probability of adoption P(n) after n recommending interactions (Pmax=0.4). Empirical data adapted from (Leskovec et al. 2006), where Pmax=0.04 (see Figure 4 for a discussion on Pmax values).

5.5

We have:

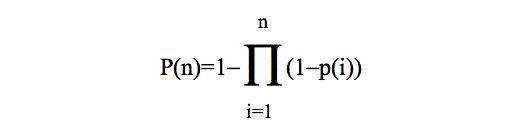
(3)

from which it is straightforward to deduce that:

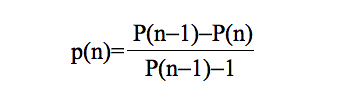
(4)

as we assume that p(i) are independent one each other. Thus, the probability of adopting at each n-th interaction with an informed neighbor is p(n).

5.6

It might be noted that empirical data used here is slightly mismatching — we eventually examine recommendation behavior over a scientific collaboration network. We acknowledge this, while it should also be irrelevant to our point, as we aim at investigating discrepancies between reality-inspired hypotheses and their traditional stylization. Anyhow, empirical data in this area is still scarce^[6], and it is likely that the continuation of this kind of study would rather involve a comparative study between various real-world behaviors (and topologies). Indeed, even in this case, a great variance should be encountered — for instance when scientists from distinct fields do not behave similarly in forming their network (e.g. mathematicians and neuroscientists (Barabási et al. 2002)), or when adoption behaviors in a similar area are to be rather dissimilar (e.g. DVDs and books (Leskovec et al. 2006)).

Models

5.7

We focus on classical threshold and cascade models. The classical models have no reason a priori to be consistent with empirical data in the general case, nonetheless one could design a stylized mechanism such that it is the closest possible to the observed behavior, fitting model parameters in this regard.

5.8

It is also noteworthy that individuals should not be necessarily eventually convinced. Some pieces of information might be less convincing than others. Adoption mechanisms should consequently be "capped" by a maximal final probability of adoption P_max, as is observed empirically ∀n, P(n) ≤ P_max and ∃ n₀, P(n₀)=P_max — after a certain number of interactions, no persuasion is possible anymore. In the original case study, P_max ≈ 0.04.

5.9

We investigate three kinds of knowledge transmission behaviors: an empirical data-based model, and corresponding best-approximation threshold and cascade models for different value of P_max. In the general case we have:

• Realistic Model (RM) P_RM(n)=P_empirical(n) corresponds to the empirical observation. p_RM(n) is computed using Eq. 3.
• Threshold Model (TM) In this model, before a given number of interactions n (the threshold), agents have no chance to adopt; past n, they adopt with probability P_max. That is, for n interactions with n ≠ ν, p(n)=0, if n=ν, p(n)=P_max. The final adoption probability is thus:

  P_TM(n)=P_maxH_ν(n)

  where H_ν is a threshold function: H_ν(n)=1 if n ≥ ν, 0 otherwise.
• Cascade Model (CM) We suggest a "capped" cascade model, that is, a cascade mechanism where the final adoption probability is bounded by P_max; thereby providing a simple way to model saturation, as decreasing cascade models do in a similar manner (Kempe et al. 2005). Thus, p(n)=p is the (fixed) probability of adopting at each interaction, but after a given number of interactions ν, p(n)=0, for n ≥ ν. The final adoption probability is thus:

  P_CM(n)=1-(1-p)^min(n,ν)

  Clearly, p=1-(1-P_max)^1/ν; thus, once P_max is chosen, CM depends on only one parameter, say ν, as TM does.

Note that in terms of the simple model (SM) presented in Section 4.10 for the study of the topology, we would have P_max =1 and, trivially, ∀n ≥ 1, both p_SM(n)=1 and P_SM(n)=1. Actually, SM is equivalently a TM with ν = 1 or a CM with p=1, ν > 0.

Simulation results

5.10

We simulated these different interaction rules on the real network 50 times, for different values of P_max. Indeed, to study the influence of P_max we use several values P_max ∈ {0.04, 0.4, 0.7, 0.99}. To design the corresponding best-approximation TM and CM for each P_max, we consider a simple homothetic transformation of the original empirical results. Then, we fit p and/or the threshold ν for both CM and TM by minimizing squared distance between the original empirical model RM and CM or TM; respectively ∑_n(P_CM(n) – P_RM(n))² and ∑_n(P_TM(n) – P_RM(n))². A graphical representation of fitted P_TM and P_CM is given on Figure 3 for P_max=0.4.

5.11

For every given P_max, we plot the average value of ρ over the 50 simulations — see Figure 4. All models converge towards an identical final state ρ(∞) ≤ P_max.

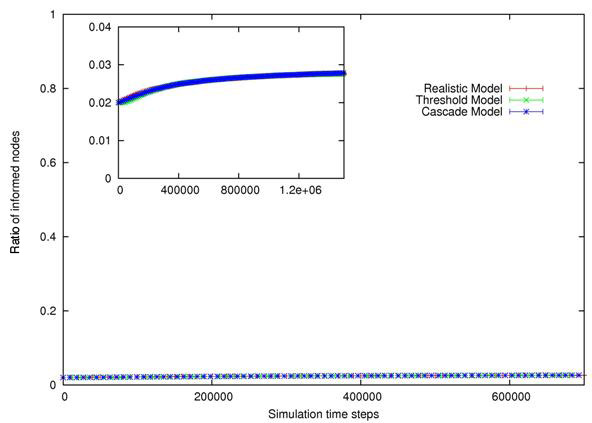
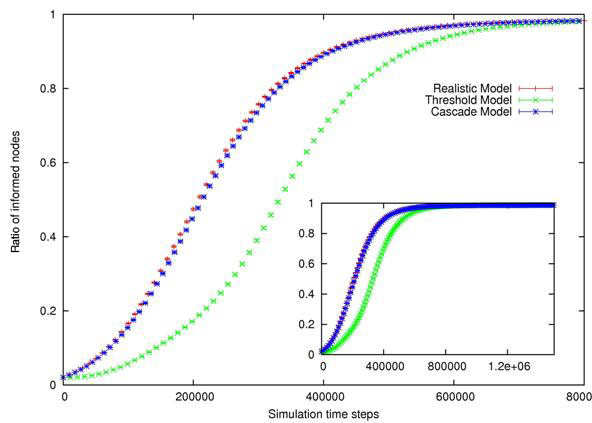
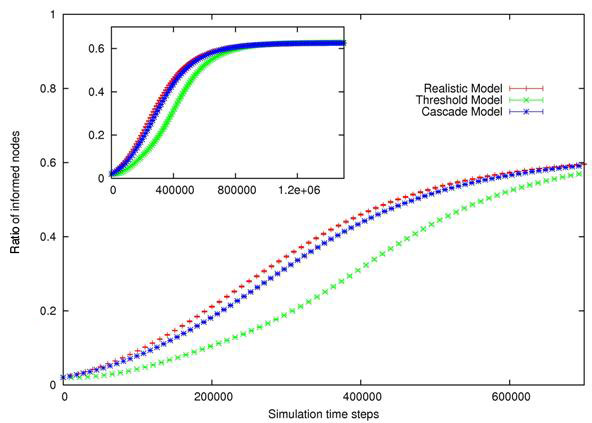
Figure 4. Evolution of ρ for RM, TM and CM, given four distinct Pmax, from left to right and from top to bottom : Pmax =0.99, Pmax =0.7, Pmax =0.4, Pmax =0.04. Confidence intervals (99%) are also shown. Insets exhibit asymptotic behavior for large time steps.

5.12

We also observe that ρ(∞) decreases with smaller values of P_max. Theoretically indeed, the expectancy of ρ(∞) is less or equal to (λ+(1 – λ)P_max), because each initially ignorant node has at most probability P_max to be convinced over the whole simulation; yet, some agents may never meet informed neighbors, especially if P_max is low, hence having no chance at all to adopt the information. As P_max decreases, the set of such isolated nodes grows, while ρ(∞)=1 for P_max =1.

5.13

Convergence is also faster when P_max increases, independently of the chosen model. Yet, as P_max increases, both RM and CM are distinct from TM. For larger P_max, TM does not provide a satisfactory model to retrieve real convergence dynamics. As plotted on Figure 5, the relative error between RM dynamics and TM or CM (computed as ||ρ_RM-ρ_TM||/||ρ_RM|| and ||ρ_RM-ρ_CM||/||ρ_RM|| respectively) invalidates TM for large P_max while it appears to approximate better RM for lower P_max. Still, CM is a better yet not perfect approximation of RM, even if the discrepancy between CM and RM seems small (Figure 3).

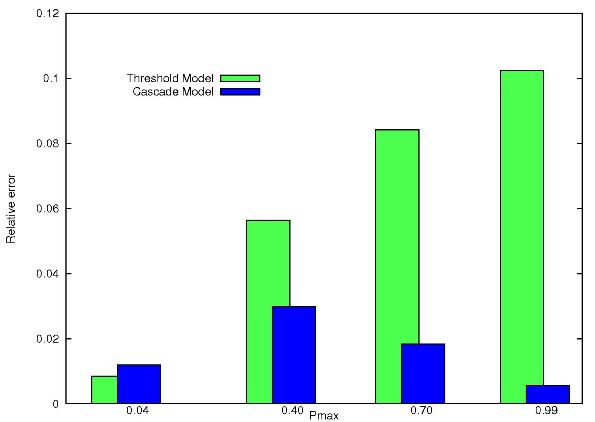
Figure 5. Relative error between Threshold and Cascade model compared to Realistic Model

5.14

Certainly, the classical TM could be improved within this kind of protocol by distinguishing various classes of agent with distinct thresholds, as in Valente's study, thus plausibly yielding better results. Many other improvements of diffusion models could be thought of: for instance for the cascade model, a decreasing probability of persuasion with the number of interactions, such as p(n)=p/αⁿ with α > 1 — see also (Kempe et al. 2003) for a generalized framework. Our aim is however not to extensively review and compare the behaviors of various classes of models, venturing into the vast collection of adoption mechanisms. Rather, we wish to show how classical assumptions like Cascade and Threshold Models may yield contrasted results; as it was with the topology: classical assumptions that scale-free features are sufficiently valid easily prove to be surprisingly erroneous with respect to realistic settings.

5.15

On the other hand, new studies may uncover radically distinct behaviors for which both TM and CM models may altogether be invalidated: Leskovec et al's data on book recommendation (2006), in particular, exhibit a decrease in the final adoption probability, indicating indeed that a higher number of interactions makes buying behavior less probable, which is thus inconsistent with the assumption that there exists an adoption probability at each step p(n)^[7]. On the whole, we suggest that future investigations of diffusion mechanisms should begin with adequate empirical protocols, then propose adapted modeling frameworks.

Conclusion

6.1

Even for the simplest transmission mechanisms, results on our two real-world social networks cast strong doubt, as counter-examples, on the efficiency of classical stylized network models. Secondly, even very basic yet credible variations between usual knowledge transmission mechanisms and realistic ones may yield sensibly distinct outputs.

6.2

More to the point,

• SF topology is usually seen as crucial improvement over ER, but actually for simple protocols, SF is like ER and still very different from RN. Community structure seems to affect results even more than degree distributions, as partially suggests EB.
• On the whole, a social network morphogenesis model successful in reproducing some real-world topological features could be deemed succesful for appraising a knowledge diffusion phenomenon only if its behavior is appraised against a real network RN. If identical, it can be taken as a valid model for the given knowledge diffusion model, and analytical solutions could follow.
• CM/TM are canonical & credible diffusion models, but actually when fitted against a realistic mechanism, they are not as accurate, even on a RN. This is particularly true for the traditional TM, even if this does certainly not mean that there may not be other situations where TM would be accurate. On the other hand, all such models may be found to be inappropriate in some settings. In contrast, relying on the empirical model may be safer than adopting prima facie any canonical model.

6.3

Beyond these conclusions, our point is also strongly epistemological, by insisting that, when it matters, empirical knowledge diffusion mechanisms should be appraised before any modeling attempt and, similarly, underlying social network topologies should, if possible, constitute an empirical benchmark. Obviously it is way beyond the scope of this paper to carry such study even on the partial typology of topologies and knowledge transmission mechanisms we sketched out in the introduction, yet, in front of the great variability in diffusion phenomena between even the most canonical and standard ones, it could be suggested that extreme care should be foremost given to empirical measurements towards realistic assumptions.

6.4

Eventually, theoretical frameworks (scale-free networks or threshold models) for which parameters are empirically fitted (exponent of the power law or the threshold itself) could be driven a priori by real-data-based mechanisms and topologies, and the subsequent simulation-based comparisons and validations.

Acknowledgements

We warmly thank Clémence Magnien and three anonymous referees for thoughtful advices. Research for this paper has been partly funded by CNRS and the University of Modena.

Notes

¹ More precisely, there is no epidemic threshold for a particular disease epidemic model (SIS, susceptible-infected-susceptible) on infinite scale-free networks. Note that this result does not hold for finite networks, nor for SIR (susceptible-infected-removed) models (May and Lloyd 2001; Eguiluz and Klemm 2002).

² This is especially relevant if the timescale of diffusion is smaller than that of social network evolution (e.g. in the case of rumors, hypes, etc.), then the social network can be considered static.

³ Wang et al. (2003) show that their model of virus diffusion is more efficient than that of Pastor-Satorras and Vespignani (2001) on various topologies, including a real computer network, while actually not directly comparing how diversely their model performs between real-world and modeled topologies. Similarly, Wu et al. (2004) simulate information propagation on a real e-mail network; yet not estimating how different the behavior would be in other kinds of (scale-free) networks.

⁴ Freely available from http://www.pubmed.com. Additionally, the particular network data used in this paper is here.

⁵ Data freely available from http://www.theyrule.net, Additionaly, the particular network data used in this paper is here.

⁶ Similarly to Leskovec et al. (2006), Backstrom et al. (2006) have measured the propension to join a "LiveJournal" community as a function of the number of friends already present in the community.

⁷ It is unclear whether such feature may or may not be accounted for by the aggregation of different categories of products and/or agents.

References

ABRAHAMSON, E. and Rosenkopf, L. (1997). Social Network Effects on the Extent of Innovation Diffusion: A Computer Simulation. Organization Science, 8(3), pp. 289-309.

AMARAL, L. A. N., Scala, A., Barthélémy, M. and Stanley, H. E. (2000). Classes of small-world networks. PNAS, 97(21), pp. 11149-11152.

AMBLARD, F. and Deffuant, G. (2004). The role of network topology on extremism propagation with the relative agreement opinion dynamics. Physica A, 343, pp. 725-738.

ANDERSON, R. M. and May, R. M. (1979). Population biology of infectious diseases. Nature, 280, pp. 361-367 & 455-461. Part I & II.

AXELROD, R. (1997). The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration. Princeton, N.J.: Princeton University Press.

BACKSTROM, L., Huttenlocher, D., Kleinberg, J. and Lan, X. (2006). Group formation in large social networks: membership, growth, and evolution. In KDD '06: Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining. New York, NY, USA: ACM Press, pp. 44-54.

BALA, V. and Goyal, S. (1998). Learning from Neighbours. Review of Economic Studies, 65(3), pp. 595-621.

BARABSI, A.-L. and Albert, R. (1999). Emergence of Scaling in Random Networks. Science, 286, pp. 509-512.

BARABASI, A.-L., Jeong, H., Ravasz, R., Neda, Z., Vicsek, T. and Schubert, T. (2002). Evolution of the social network of scientific collaborations. Physica A, 311, pp. 590-614.

BARBOUR, A. and Mollison, D. (1990). Epidemics and random graphs. In J.-P. Gabriel, C. Lefevre and P. Picard (Eds.) Stochastic Processes in Epidemic Theory, Lecture Notes in Biomaths, 86. Springer, pp. 86-89.

BARTHELEMY, M., Barrat, A., Pastor-Satorras, R. and Vespignani, A. (2005). Dynamical patterns of epidemic outbreaks in complex heterogeneous networks. Journal of Theoretical Biology, 235, p. 275.

BOGUNA, M. and Pastor-Satorras, R. (2002). Epidemic spreading in correlated complex networks. Physical Review E, 66, p. 047104.

BOGUNA, M., Pastor-Satorras, R., Diaz-Guilera, A. and Arenas, A. (2004). Models of social networks based on social distance attachment. Physical Review E, 70, p. 056122.

BOLLOBAS, B. (1985). Random Graphs. London: Academic Press.

BURT, R. S. (1987). Social Contagion and Innovation: Cohesion Versus Structural Equivalence. American Journal of Sociology, 92(6), pp. 1287-1335.

COLEMAN, J., Katz, E. and Menzel, H. (1957). The Diffusion of an Innovation Among Physicians. Sociometry, 20(4), pp. 253-270.

COWAN, R. and Jonard, N. (2004). Network structure and the diffusion of knowledge. Journal of Economic Dynamics and Control, 28, pp. 1557-1575.

CREPEY, P., Alvarez, F. P. and BarthÈlemy, M. (2006). Epidemic variability in complex networks. Physical Review E, 73(4), p. 046131.

DEFFUANT, G. (2006). Comparing Extremism Propagation Patterns in Continuous Opinion Models. Journal of Artificial Societies and Social Simulation, 9(3), p. 8.

DEFFUANT, G., Amblard, F., Weisbuch, G. and Faure, T. (2002). How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5(4), p. 1.

DELGADO, J. (2002). Emergence of social conventions in complex networks. Artificial Intelligence, 141, pp. 171-185.

DEROIAN, F. (2002). Formation of social networks and diffusion of innovations. Research Policy, 31, pp. 835-846.

DOROGOVTSEV, S. N. and Mendes, J. F. F. (2003). Evolution of Networks: From Biological Nets to the Internet and WWW. Oxford University Press, Oxford.

EGUILUZ, V. M. and Klemm, K. (2002). Epidemic threshold in structured scale-free networks. Physical Review Letters, 89, p. 108701.

ELLISON, G. and Fudenberg, D. (1995). Word-of-Mouth Communication and Social Learning. Quarterly Journal of Economics, 110(1), pp. 93-125.

ERDÖS, P. and Rényi, A. (1959). On random graphs. Publicationes Mathematicae, 6, pp. 290-297.

GANESH, A., Massoulié, L. and Towsley, D. (2005). The effect of network topology on the spread of epidemics. In IEEE Infocom, vol. 2. pp. 1455-1466.

GILBERT, N., Pyka, A. and Ahrweiler, P. (2001). Innovation Networks — A Simulation Approach. Journal of Artificial Societies and Social Simulation, 4(3), p. 8.

GOLDENBERG, J., Libai, B. and Muller, E. (2001). Talk of the network: A complex systems look at the underlying process of word-of-mouth. Marketing Letters, 12(3), pp. 211-223.

GRANOVETTER, M. (1987). Threshold models of collective behavior. American Journal of Sociology, 83(6), pp. 1420-1443.

GRANOVETTER, M. S. (1973). The Strength of Weak Ties. The American Journal of Sociology, 78(6), pp. 1360-1380.

GRUHL, D., Guha, R., Liben-Nowell, D. and Tomkins, A. (2004). Information Diffusion Through Blogspace. In WWW2004: Proceedings of the 13th Intl Conf on World Wide Web. NYC, NY, USA, pp. 491-501.

GUILLAUME, J.-L. and Latapy, M. (2004). Bipartite structure of all complex networks. Information Processing Letters, 90(5), pp. 215-221.

GUIMERA, R., Uzzi, B., Spiro, J. and Amaral, L. A. N. (2005). Team Assembly Mechanisms Determine Collaboration Network Structure and Team Performance. Science, 308, pp. 697-702.

HETHCOTE, H. W. (2000). The Mathematics of Infectious Diseases. SIAM Review, 42(4), pp. 599-653.

HOLME, P., Edling, C. R. and Liljeros, F. (2004). Structure and time evolution of an Internet dating community. Social Networks, 26, pp. 155-174.

KEELING, M. J. and Eames, K. T. D. (2005). Networks and epidemics models. Journal of the Royal Society Interface, 2, pp. 295-307.

KEMPE, D., Kleinberg, J. and Tardos, E. (2003). Maximizing the spread of influence through a social network. In KDD '03: Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining. New York, NY, USA: ACM Press, pp. 137-146.

KEMPE, D., Kleinberg, J. and Tardos, E. (2005). Influential Nodes in a Diffusion Model for Social Networks. In ICALP, vol. 3580 of Lecture Notes in Computer Science. Springer, pp. 1127-1138.

KEMPE, D. and Kleinberg, J. M. (2002). Protocols and Impossibility Results for Gossip-Based Communication Mechanisms. In I. C. Society (Ed.) FOCS '02: Proceedings of the 43rd Symposium on Foundations of Computer Science. Washington, DC, USA, pp. 471-480.

KLEMM, K., Eguiluz, V. M., Toral, R. and Miguel, M. S. (2005). Globalization, polarization and cultural drift. Journal of Economic Dynamics and Control, 29, pp. 321-334.

KOSSINETS, G. and Watts, D. J. (2006). Empirical Analysis of an Evolving Social Network. Science, 311, pp. 88-90.

LESKOVEC, J., Adamic, L. A. and Huberman, B. A. (2006). The Dynamics of Viral Marketing. In ACM Conference on Electronic Commerce. pp. 228-237.

LEW, B. (2000). The Diffusion of Tractors on the Canadian Prairies: The Threshold Model and the Problem of Uncertainty. Explorations in Economic History, 37(2), pp. 189-216.

LIND, P. G., Gonzalez, M. C. and Herrmann, H. J. (2005). Cycles and clustering in bipartite networks. Physical Review E, 72, p. 056127.

LLOYD, A. L. and May, R. M. (2001). How Viruses Spread Among Computers and People. Science, 292(5520), pp. 1316-1317.

MAY, R. M. and Lloyd, A. L. (2001). Infection dynamics on scale-free networks. Physical Review E, 64(6), p. 066112.

MOLLOY, M. and Reed, B. (1995). A critical point for random graphs with a given degree sequence. Random Structures and Algorithms, 161(6), pp. 161-179.

MORRIS, S. (2000). Contagion. Review of Economic Studies, 67(1), pp. 57-78.

NEWMAN, M. E. J. (2002). Spread of Epidemic Disease on Networks. Physical Review E, 66(016128).

NEWMAN, M. E. J. (2003). Ego-centered networks and the ripple effect — or — Why all your friends are weird. Social Networks, 25, pp. 83-95.

NEWMAN, M. E. J. and Park, J. (2003). Why social networks are different from other types of networks. Physical Review E, 68(036122).

NEWMAN, M. E. J., Strogatz, S. and Watts, D. (2001). Random graphs with arbitrary degree distributions and their applications. Physical Review E, 64(026118).

PASTOR-SATORRAS, R. and Vespignani, A. (2001). Epidemic Spreading in Scale-Free Networks. Physical Review Letters, 86(14), pp. 3200-3203.

PASTOR-SATORRAS, R. and Vespignani, A. (2002). Epidemic dynamics in finite size scale-free networks. Physical Review E, 65, p. 035108.

REDNER, S. (2005). Citation Statistics from 110 Years of Physical Review. Physics Today, 58, pp. 49-54.

ROBERTSON, T. S. (1967). The Process of Innovation and the Diffusion of Innovation. Journal of Marketing, 31(1), pp. 14-19.

ROBINS, G. and Alexander, M. (2004). Small Worlds Among Interlocking Directors: Network Structure and Distance in Bipartite Graphs. Computational and Mathematical Organization Theory, 10, pp. 69-94.

ROGERS, E. M. (1976). New Product Adoption and Diffusion. The Journal of Consumer Research, 2(4), pp. 290-301.

ROGERS, E. M. (2003). Diffusion of Innovations, 5th Edition. Free Press.

SZENDRÖI, B. and Csányi, G. (2004). Polynomial epidemics and clustering in contact networks. Proceedings of the Royal Society London, B Biological sciences, 271, pp. S364-S366.

VALENTE, T. W. (1995). Network Models of the Diffusion of Innovations. Hampton Press.

VALENTE, T. W. (1996). Social network thresholds in the diffusion of innovations. Social Networks, 18, pp. 69-89.

WANG, Y., Chakrabarti, D., Wang, C. and Faloutsos, C. (2003). Epidemic Spreading in Real Networks: An Eigenvalue Viewpoint. In Proceedings of the 22nd Symposium on Reliable Distributed Systems (SRDS 2003). IEEE Computer Society, pp. 25-34.

WASSERMAN, S. and Faust, K. (1994). Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.

WATTS, D. J. and Strogatz, S. H. (1998). Collective dynamics of "small-world" networks. Nature, 393, pp. 440-442.

WHITE, D. R., Kejzar, N., Tsallis, C., Farmer, D. and White, S. D. (2006). A generative model for feedback networks. Physical Review E, 73, p. 016119.

WU, F., Huberman, B. A., Adamic, L. A. and Tyler, J. R. (2004). Information Flow in Social Groups. Physica A, 337, pp. 327-335.

ZEGURA, E. W., Calvert, K. L. and Bhattacharjee, S. (1996). How to Model an Internetwork. In IEEE Infocom, vol. 2. San Francisco, CA: IEEE, pp. 594-602.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2007]