András Németh and Károly Takács (2007)
The Evolution of Altruism in Spatially Structured Populations
Journal of Artificial Societies and Social Simulation
vol. 10, no. 3 4
<https://www.jasss.org/10/3/4.html>
For information about citing this article, click here
Received: 30-Oct-2006 Accepted: 21-May-2007 Published: 30-Jun-2007
 Abstract
Abstract
|
|
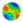
Figure 1. Dyadic Interaction of Teaching K implies increased survival chances. |

|
|
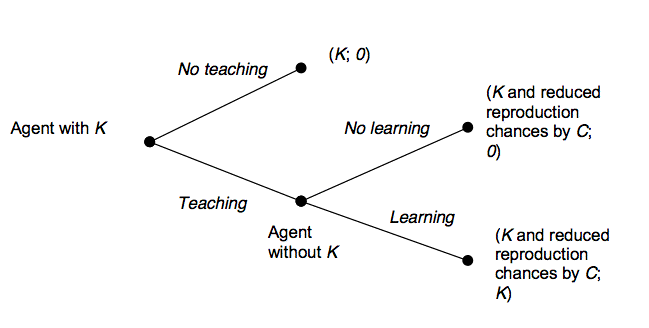
Figure 2. 10000 years of Business as Usual: Success of Altruistic Teachers Scenario 2, the four genotypes (TL: yellow, L: green, T: red, and 0: black) are approximately equally represented in the initial population of 100 agents. 0-types (black) are invaded by T-types (red) in times without knowledge. This is followed by an invasion of TL-types (yellow) and accumulation of knowledge, with the invasion of L-types(green) before year 10000. Meanwhile there are a lot of unsuccessful bids for power. Altruistic teachers have an overwhelming majority significantly longer than others. In this example: mutation rate: 0.1%; innovation rate: 0.1%; breeding range: 20 pixels; teaching range: 32 pixels; a T-gene calls for teaching with a probability of 0.5 and teaching decreases breeding chances by 10%. The domination of yellows (TL) is robust for changes in the auxiliary parameter values. |
|
|
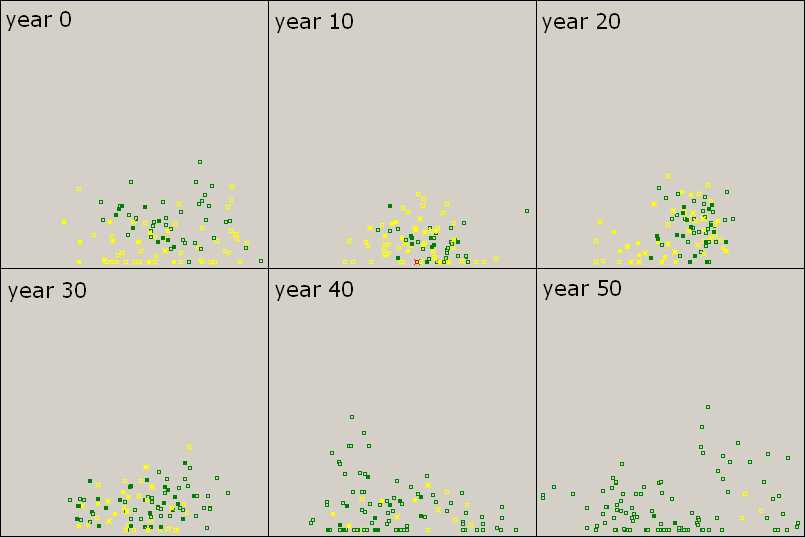
Figure 3. Triumph of Free Riders Filled squares represent agents with knowledge. Green agents (L) exploit yellows (TL) gradually (years 0-30). As TL-types diminish, knowledge among greens becomes scarce (year 40). By the end, L-types attain an overwhelming success, but have no knowledge (year 50). Scenario 2, the initial population consists of approximately the same number of TL-types and L-types. Parameter values are the same as before. |
|
|
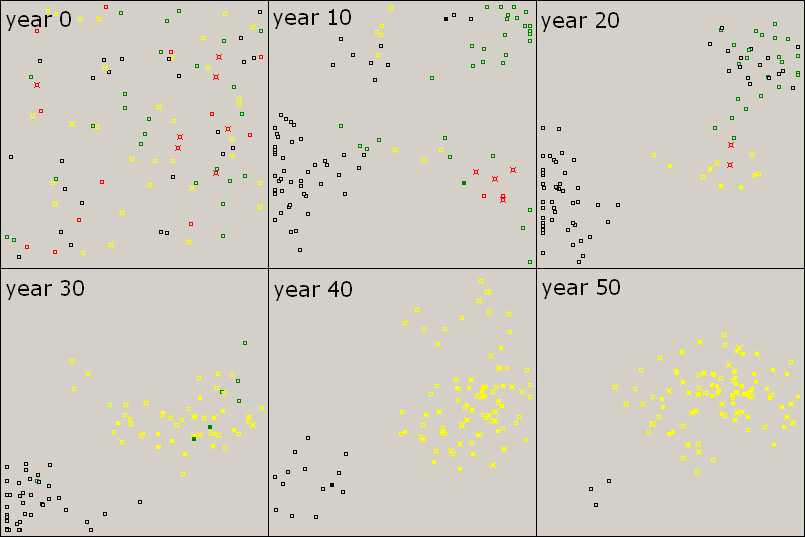
Figure 4. Knowledge is Power Starting from a random mix of agents (year 0), genotypes become segregated, since new agents are born close to their parents (year 10). Knowledge appears among yellows (TL) due to innovation and teaching, while greens (L) are mixed with blacks (0) (year 20). Although some greens acquire knowledge in year 30, they die out (year 40) and yellows prevail (year 50). Parameter values are the same as before. |
|
|
|
Figure 5. The Effect of Population Size Proximity based interaction, starting from a random mix of agents (year 0). Parameter values are the same as before with varying population size. |
|
|
|
Figure 6. Probabilities of Different Proportional Distributions of Agents by Population Size Number of agents are on the horizontal axis ranging from 0 to population size and probabilities (frequencies) are on the vertical axis. Proximity based interaction, starting from a random mix of agents (year 0), for the same runs as in Figure 5. Parameter values are the same as before with varying population size. |
|
|
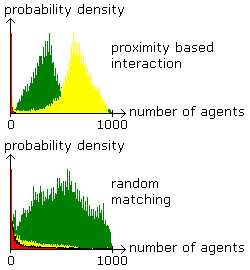
Figure 7. Mixed Equilibrium in a Large Population Proximity based interaction in a spatially structured population (above) is a key for success of the TL-types (yellow) also in a large population. They have to share the space with L-types (green). L-types gain success among the population in case of random matching (below). Parameter values are the same as before except that there are 1000 agents. |
|
|
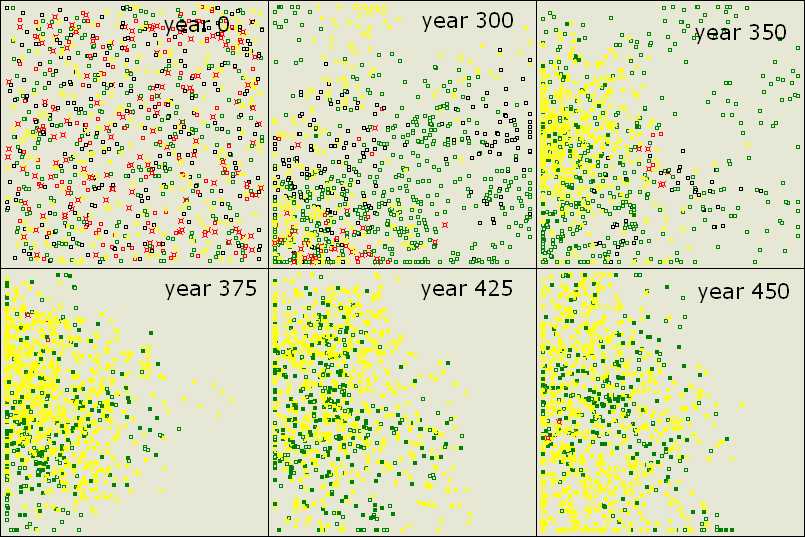
Figure 8. Exploitation and Recovery of Altruistic Teachers After a random start (year 0) and random processes, yellows (TL) attain success and accumulate knowledge (year 350-375). Greens (L) are efficient in free riding (year 425), but altruistic teachers recover by establishing centers of knowledge at new locations (year 450). Parameter values are the same as before except population size (1000). |

|
|
Figure 9. Genotypes Live Side by Side in Large Populations Increasing population size results in the coexistence of yellows (TL) and greens (L). This example is for the simulation run represented in Figure 8. |
|
|
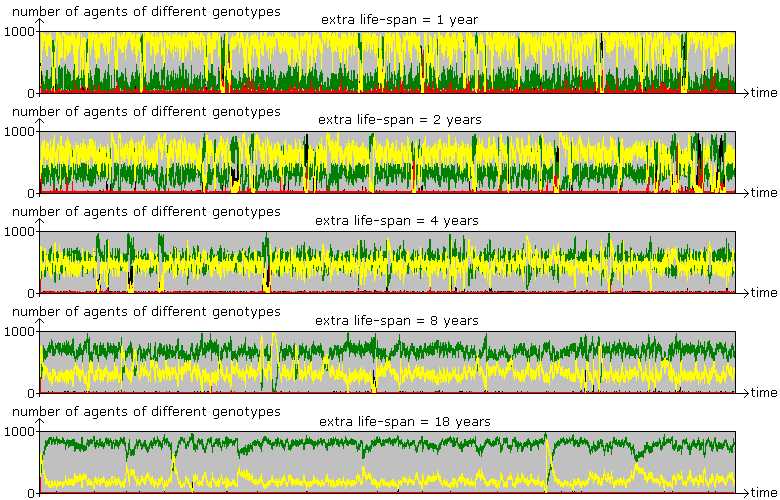
Figure 10. The Paradox of Knowledge By increasing the value of knowledge in terms of extra life-span, the proportion of greens (L) increases in the mixed equilibrium. Parameter values are the same as before with the population size of 1000. |
|
|
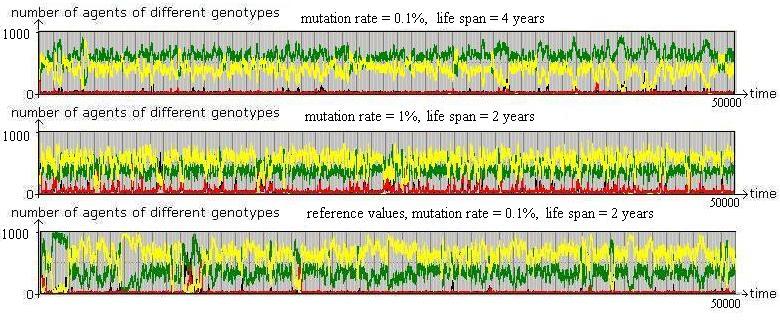
Figure 11. Illustrative tests of robustness Proximity based interaction, starting from a random mix of agents (year 0) with a population size of 1000. The lower part shows results for the reference parameter values. In the middle, the mutation rate is changed from 0.1% to 1%. In the upper part, lifetimes of agents are doubled. All other parameter values are fixed as before. |
for (every living_agent x): if (random(1000) < innovation_rate) x.knowledge:=1; if ((x.teacher) && (x.knowledge=1)): repeat // search for an agent without knowledge if (proximity_based) y := random_agent_in_proximity else y := random_agent; until (y.knowledge = 0) if (y.learning) y.knowledge := 1; x.breeading_chance := x.breeading_chance - costs; end if end for
2 For parameter values as in Figure 3, without knowledge at the start and with random matching, the total length of regimes of the TL, L, and 0 genotypes are approximately the same.
3 The analysis has been replicated by omitting variation on the L-gene, thus “switching off” genotypes T and 0. In small populations, L-types are relatively more successful with switching off than without switching off variation in the learning gene, but their chances to attain dominance lags behind the chances of TL-types in a spatially structured population. Results about the evolution of altruistic teaching in large populations do not differ from the presented results when genotypes T and 0 are excluded.
4 For the assumed parameter values in a small population, regimes of the TL-types last four times longer than regimes of the L or 0 genotypes and more than six times longer than T-regimes. Results confirm that learning from others (expressed by the L-gene) is successful, but the gain from the capacity of learning is negligible if there is no knowledge around.
AXELROD, R. & Hamilton, W. D. (1981). The evolution of cooperation. Science, 211, 1390-1396.
AXELROD, R., Hammond, R. A., & Grafen, A. (2004). Altruism via Kin-Selection Strategies that Rely on Arbitrary Tags with which They Coelvolve. Evolution, 58(8): 1833-1838.
BACK, I. & Flache, A. (2006). The Evolution of Cooperation Based on Interpersonal Commitment. Journal of Artificial Societies and Social Simulation, 9(1), https://www.jasss.org/9/1/12.html.
BEARMAN, P. (1997). Generalized exchange. American Journal of Sociology 102, 1383-1415.
BECKER, G. S. (1976). Altruism, egoism, and genetic fitness: Economics and sociobiology. Journal of Economic Literature, 14, 817-826.
BOWLES, S. & Gintis, H. (1998). The moral economy of communities: Structured populations and the evolution of pro-social norms. Evolution and Human Behavior, 19, 3-25.
BOWLES, S. & Gintis, H. (2003). The origins of human cooperation. In P. Hammerstein (Ed.), The Genetic and Cultural Origins of Cooperation. Cambridge, MA: MIT Press.
BOYD, R. & Richerson, P. J. (1985). Culture and the Evolutionary Process. Chicago: Chicago University Press.
BOYD, R. & Richerson, P. J. (1989). The evolution of indirect reciprocity. Social Networks, 11: 213-236.
CASTRO, L. & Toro, M. A. (2004). The evolution of culture: From primate social learning to human culture. Proceedings of the National Academy of Sciences of the U.S.A.,101, 10235-10240.
CAVALLI-SFORZA, L. L. & Feldman, M. (1981). Cultural Transmission and Evolution: A Quantitative Approach, Princeton: Princeton University Press.
CONTE, R. (2002). Agent-based modeling for understanding social intelligence. Proceedings of the National Academy of Sciences of the U.S.A.,99, 7189-7190.
CONTE, R. & Paolucci, M. (2001). Intelligent social learning. Journal of Artificial Societies and Social Simulation, 4(1), https://www.jasss.org/4/1/3.html
DAWKINS, R. (1976). The Selfish Gene. Oxford: Oxford University Press.
DE VOS, H. & Zeggelink, E. (1997). Reciprocal altruism in human social evolution: The viability of reciprocal altruism with a preference for "old-helping-partners". Evolution and Human Behavior, 18, 261-278.
DE VOS, H., Smaniotto, R. C., & Elsas, D. (2001). Reciprocal altruism under conditions of partner selection. Rationality & Society, 13, 139-183.
DOEBELI, M. & Hauert, C. (2005). Models of cooperation based on the Prisoner's Dilemma and the Snowdrift game. Ecology Letters, 8 (7): 748-766.
FLACHE, A. (2004). Stylized solutions for environmental dilemmas in a cellular world. In R. Suleiman, D. Budescu, D. Messick, & Fischer, I. (Eds.): Contemporary Psychological Research on Social Dilemmas. Cambridge: Cambridge University Press.
FLACHE, A. & Hegselmann, R. (1999). Rationality vs. learning in the evolution of solidarity networks: A theoretical comparison. Computational and Mathematical Organization Theory, 5, 97-127.
FRANK, R. (2003). Microeconomics and Behaviour. 5th edition. New York: McGraw-Hill.
GINTIS, H. (2000). Strong reciprocity and human sociality. Journal of Theoretical Biology, 206, 169-179.
GRAFEN, A. (1985). A Geometric View of Relatedness. Oxford Surveys in Evolutionary Biology, 2:28-90.
HAMILTON, W. D. (1964a). The genetical evolution of social behavior: I. Journal of Theoretical Biology, 7, 1-16.
HAMILTON, W. D. (1964b). The genetical evolution of social behavior: II. Journal of Theoretical Biology, 7, 17-52.
HEGSELMANN, R. (1996). Social dilemmas in Lineland and Flatland. In W. B. G. Liebrand, & D. M. Messick, (Eds.): Frontiers in Social Dilemma Research. Berlin: Springer.
HENRICH, J. (2004). Cultural group selection, coevolutionary processes and large-scale cooperation. Journal of Economic Behavior and Organization, 53,3-35.
HENRICH, J. & Gil-White, F. (2001). The evolution of prestige: freely conferred status as a mechanism for enhancing the benefits of cultural transmission. Evolution and Human Behavior, 22, 1-32.
HEYES, C. (2001). Causes and consequences of imitation. Trends in Cognitive Sciences, 5, 253-261.
HUBERMANN, B.A. & Glance, N.S. (1993). Evolutionary games and computer simulations. Proceedings of the National Academy of Sciences of the U.S.A., 90, 7712-7715.
KAPLAN, H. & Hill, K. (1985). Food sharing among Ache foragers: Tests of explanatory hypotheses. Current Anthropology, 26, 223-246.
MACY, M. W. & Skvoretz, J. (1998). The evolution of trust and cooperation between strangers: a computational model. American Sociological Review, 63, 638-660.
MAYNARD Smith, J. & Price, G. R. (1973). The logic of animal conflict. Nature, 246, 15-18.
NOWAK, M. & May, R. (1992). Evolutionary games and spatial chaos. Nature, 359, 826-829.
NOWAK, M. & May, R. (1993). The spatial dilemmas of evolution. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering, 3, 35-78.
NOWAK, M. & Sigmund, K. (1998). Evolution of indirect reciprocity by image scoring. Nature, 393, 573-576.
NOWAK, M.A., Bonhoeffer, S. & May, M. (1994). Spatial games and the maintenance of cooperation. Proceedings of the National Academy of Sciences of the U.S.A., 91, 4877-4881.
RAPOPORT, A., Diekmann, A., & Franzen, A. (1995). Experiments with social traps IV. Reputation effects in the evolution of cooperation. Rationality & Society, 7, 431-441.
RAUB, W. & Weesie, J. (1990). Reputation and efficiency in social interaction: an example of network effects. American Journal of Sociology, 96, 626-654.
SIMON, H. A. (1990). A mechanism for social selection and successful altruism. Science, 250 (4988): 1665-1668.
TOMASELLO, M., Kruger, A. C., & Ratner, H. H. (1993). Cultural learning. Behavioral and Brain Sciences, 16, 495-552.
TRIVERS, R. L. (1971). The evolution of reciprocal altruism. Quarterly Review of Biology, 46, 35-57.
WEDEKIND, C. & Milinski, M. (2000). Cooperation through image scoring in humans. Science, 288, 850-852.
YAMAGISHI, T. & Cook, K. S. (1993). Generalized exchange and social dilemmas. Social Psychology Quarterly, 56, 235-248.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]