Jijun Zhao, Ferenc Szidarovszky and Miklos N. Szilagyi (2007)
Finite Neighborhood Binary Games: a Structural Study
Journal of Artificial Societies and Social Simulation
vol. 10, no. 3 3
<https://www.jasss.org/10/3/3.html>
For information about citing this article, click here
Received: 22-Jun-2006 Accepted: 11-Feb-2007 Published: 30-Jun-2007
 Abstract
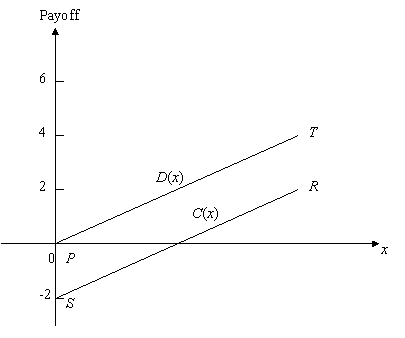
Abstract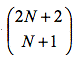 possibilities for mixing the two sequences. If we assume furthermore that both functions are linear, then this number can be reduced. Merlone et al. (2007) discuss this case and give a tight upper bound for this number. Similar situations occur if the payoffs of each agent depend on the ratio of cooperators in a defined neighborhood about the agent. In this case N has to be replaced by the number of agents located in the neighborhood. If both functions C and D are linear (see Figure 1, where C(x)=(R-S)x+S and D(x)=(T-P)x+P), then the games are well defined by the numbers P=D(0), T=D(1), S=C(0) and R=C(1).
possibilities for mixing the two sequences. If we assume furthermore that both functions are linear, then this number can be reduced. Merlone et al. (2007) discuss this case and give a tight upper bound for this number. Similar situations occur if the payoffs of each agent depend on the ratio of cooperators in a defined neighborhood about the agent. In this case N has to be replaced by the number of agents located in the neighborhood. If both functions C and D are linear (see Figure 1, where C(x)=(R-S)x+S and D(x)=(T-P)x+P), then the games are well defined by the numbers P=D(0), T=D(1), S=C(0) and R=C(1).
|
| Figure 1. Payoff functions |
|
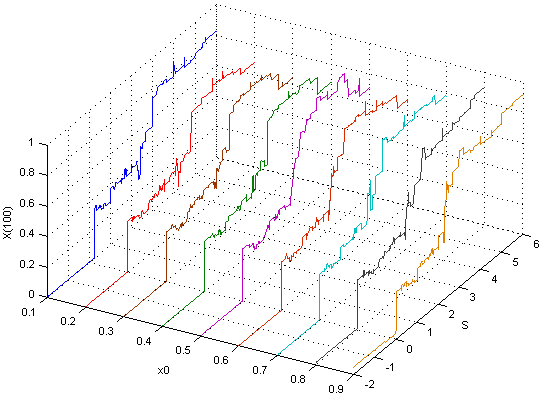
| Figure 2. x(100) as a function of S with varying value of x(0) |
| Table 1: The trajectory center of the last 20 iterations for different values of S and x(0) | ||||||||
| S | average of x | std | ||||||
| x0=0.2031 | x0=0.2999 | x0=0.4 | x0=0.5898 | x0=0.7017 | x0=0.7969 | x0=0.8991 | ||
| 0.01 | 0.3309 | 0.305 | 0.3171 | 0.3142 | 0.3137 | 0.3183 | 0.3097 | 0.008128 |
| 0.1 | 0.3309 | 0.305 | 0.3171 | 0.3142 | 0.3137 | 0.3183 | 0.3097 | 0.008128 |
| 0.2 | 0.3309 | 0.305 | 0.3171 | 0.3142 | 0.3137 | 0.3183 | 0.3097 | 0.008128 |
| 0.3 | 0.3151 | 0.3195 | 0.3311 | 0.3189 | 0.3215 | 0.3226 | 0.3282 | 0.00554 |
| 0.4 | 0.3193 | 0.3073 | 0.3205 | 0.3063 | 0.3188 | 0.3119 | 0.3158 | 0.005841 |
| 0.5 | 0.2993 | 0.3001 | 0.2931 | 0.3116 | 0.2928 | 0.3011 | 0.2918 | 0.006929 |
| 0.6 | 0.2838 | 0.2846 | 0.2923 | 0.2919 | 0.2791 | 0.3023 | 0.2927 | 0.007663 |
| 0.7 | 0.3009 | 0.3064 | 0.3064 | 0.293 | 0.2988 | 0.2927 | 0.3013 | 0.005599 |
| 0.8 | 0.2929 | 0.2905 | 0.2941 | 0.2985 | 0.2905 | 0.2905 | 0.2897 | 0.003122 |
| 0.9 | 0.293 | 0.2905 | 0.2917 | 0.2985 | 0.294 | 0.2905 | 0.2877 | 0.003411 |
| 1 | 0.3157 | 0.3147 | 0.3152 | 0.3209 | 0.3137 | 0.3158 | 0.3216 | 0.003126 |
| 1.1 | 0.3468 | 0.347 | 0.3411 | 0.3457 | 0.3491 | 0.3448 | 0.3438 | 0.002571 |
| 1.2 | 0.3651 | 0.3531 | 0.3542 | 0.342 | 0.3548 | 0.3497 | 0.3618 | 0.007605 |
| 1.3 | 0.3612 | 0.3544 | 0.3592 | 0.3597 | 0.3577 | 0.3578 | 0.36 | 0.002213 |
| 1.4 | 0.3565 | 0.3594 | 0.364 | 0.3602 | 0.3565 | 0.3646 | 0.3626 | 0.003336 |
| 1.5 | 0.369 | 0.3695 | 0.3741 | 0.3723 | 0.3664 | 0.3697 | 0.3701 | 0.002458 |
| 1.6 | 0.3575 | 0.3571 | 0.3594 | 0.3609 | 0.3542 | 0.3593 | 0.3624 | 0.002697 |
| 1.7 | 0.384 | 0.3786 | 0.3867 | 0.3911 | 0.3834 | 0.3826 | 0.3782 | 0.004494 |
| 1.8 | 0.3909 | 0.3922 | 0.3889 | 0.3818 | 0.3852 | 0.3836 | 0.3899 | 0.003966 |
| 1.9 | 0.3909 | 0.3922 | 0.3889 | 0.3818 | 0.3852 | 0.3836 | 0.3899 | 0.003966 |
| 1.99 | 0.3909 | 0.3922 | 0.3889 | 0.3818 | 0.3852 | 0.3836 | 0.3899 | 0.003966 |
| std | 0.035286 | 0.037074 | 0.035114 | 0.033596 | 0.035327 | 0.033676 | 0.036484 | |
|
|
|
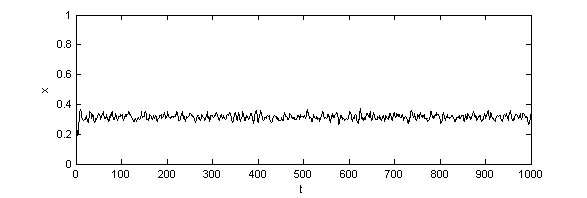
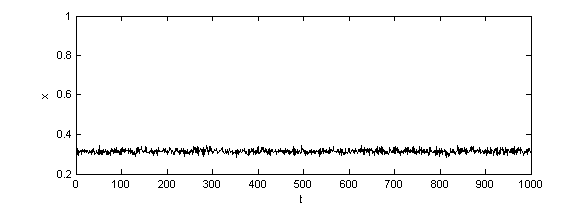
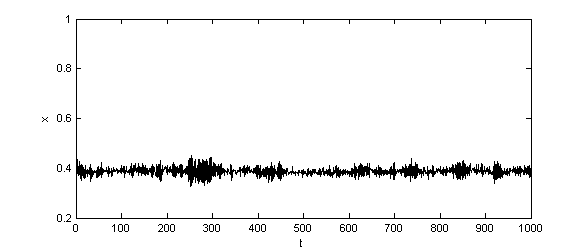
| Figure 3. Time series of x with different values of S (a)S=0.01 (b)S=1 (c)S=1.99 |
|
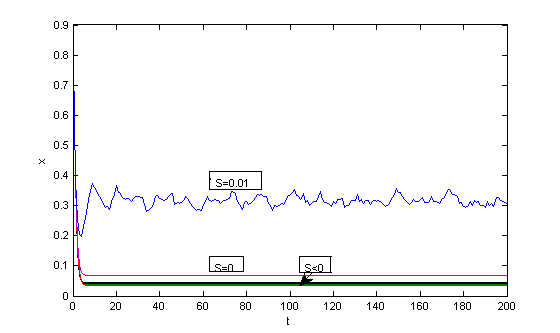
| Figure 4. Time series of the ratios of cooperators when S<0, S=0 and S=0.01 |
|
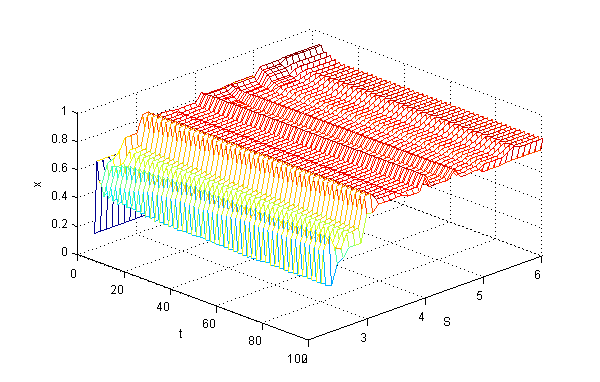
| Figure 5. 3D plot of x as function of t and S, 2.3≤S≤6, x(0)=0.1 |

|
| Figure 6. 3D plot of x as function of t and S, 2.3≤S≤6, x(0)=0.5 |
|
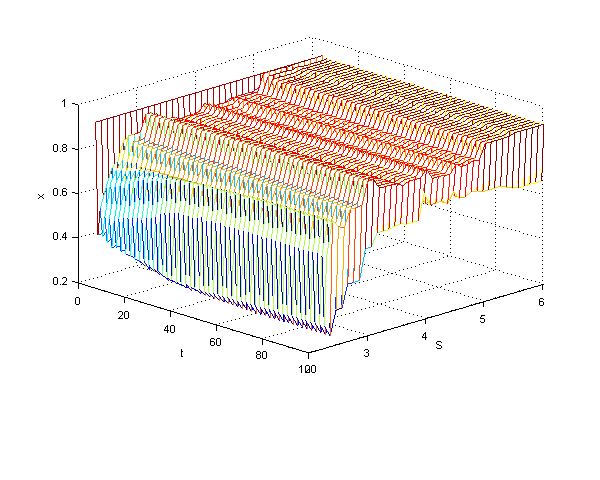
| Figure 7. 3D plot of x as function of t and S, 2.3≤S≤6, x(0)=0.9 |
|
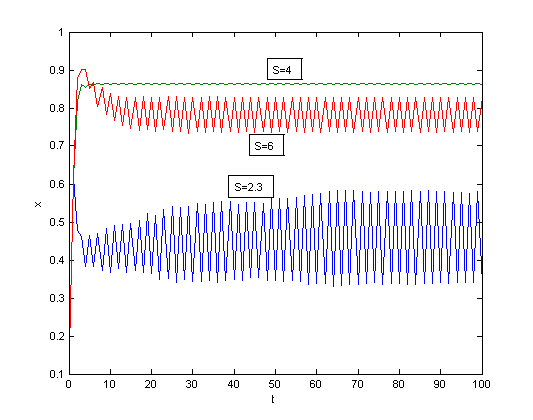
| Figure 8. Comparison of time series patterns of x with different S values, x(0)=0.1 |
.png)
|
(1) |
While in the case of greedy agents all trajectories are deterministic, in the case of Pavlovian agents they are random, since the behavior of the agents is determined by the probability values (1). Each simulation can produce different trajectory, therefore we made 16 runs with identical P(0)=0.5 for all agents and computed the average values of the x(t) ratios for all t. If x*(t) denotes the "true" expectation and xaverage(t) the average value computed from NS simulation runs, then from the Chebyshev inequality we know that with any ε>0,
.png)
|
(2) |
where σ2(t) is the variance of the x(t) values. In our case σ2(t) was approximated by the sample variance, which was very small, less than 10-6, since the different simulation runs were very similar. Notice that we had 10,000 agents, therefore, the relative frequencies were calculated from a very large sample size. The values of x(t) are then accurate for at least 2 decimal figures with 99.9% probability.
|
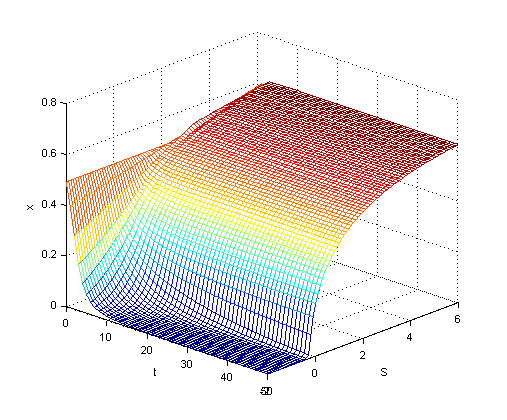
| Figure 9. 3D plot of x as function of t and S, agents are Pavlovian |
HELBING D, Farkas I and Vicsek T (2000) Simulating Dynamical Features of Escape Panic. Nature, 407. pp. 487-490.
KITTS J A (1999) Structural Learning: Attraction and Conformity in Task-Oriented Groups. Computational & Mathematical Organization Theory, 5(2). pp. 129-145.
MERLONE U, Szidarovszky F and Szilagyi M N (2007) Finite Neighborhood Games with Binary Choices. Submitted to Mathematica Pannonica.
PANZARASA P, Jennings N R and Norman T J (2001) Social Mental Shaping: Modeling the Impact of Sociality on the Mental States of Autonomous Agents. Computational Intelligence, 17(4). pp. 738-782.
PANZARASA P and Jennings N R (2001) Social Influence and the Generation of Joint Mental Attitudes in Multi-agent Systems. Proceeding of the Eurosim Workshop on Simulating Organisational Processes, Delft, The Netherlands.
RAPOPORT A and Guyer M (1966) A Taxonomy of 2*2 Games. General Systems, 11. pp. 203-214.
SZILAGYI M N and Szilagyi Z C (2000) A Tool for Simulated Social Experiments. Simulation, 74. pp. 4-10.
SZILAGYI M N (2003) An Investigation of N-person Prisoners' Dilemmas. Complex Systems, 14. pp. 155-174.
SZILAGYI M N (2005) From Two-Person Games to Multi-Player Social Phenomena (in Hungarian). Beszelo, 10(6-7). pp. 88-98.
SZILAGYI M N (2007) Agent Based Simulation of the N-person Chicken Dilemma Game. In Jorgensen S, Quincampoix M and Vincent T L (Eds.) Advances in Dynamic Game Theory, Birkhauser: Boston. pp. 695-703.
ZHAO J, Szilagyi M N and Szidarovszky F (2007) A Continuous Model of N-Person Prisoners' Dilemma. Game Theory and Applications (in press).
ZIZZO D J (2006) You Are Not in My Boat: Common Fate and Discrimination Against Outgroup Members. Working Paper, School of Economics, University of East Anglia, Norwich, U.K.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]