Gilbert Peffer and Bàrbara Llacay (2007)
Higher-Order Simulations: Strategic Investment Under Model-Induced Price Patterns
Journal of Artificial Societies and Social Simulation
vol. 10, no. 2, 6
<https://www.jasss.org/10/2/6.html>
For information about citing this article, click here
Received: 24-Feb-2006 Accepted: 03-Mar-2007 Published: 31-Mar-2007
 Abstract
Abstract|
|
(1) |
where the prices Bt(1) and Bt(2) for both bonds are set by a market maker in accordance to a linear price formation rule. Although other formulations are possible (see e.g. Madhavan 2000 for a survey), we use the simplest one, which states that prices have to rise (fall) in the presence of over-demand (over-supply) by an amount that is inversely proportional to the liquidity of the traded security. Here, we do not take into account the inventory of the market maker nor the presence of information asymmetries in the market, and thus assume bid-ask spreads to be zero. Bond prices are updated according to:
|
|
(2) |
where Θt+1(i) is the total time-t+ excess order — the sum of all orders emitted in the time interval (t, t+1) — of bond i and λ(i) is a constant liquidity factor that accounts for the depth of the market in bond i. One disadvantage of this linear formulation is that prices can become negative, which could be avoided by using a log-price formulation for the price formation rule. Outstanding orders in any given trading interval are always filled at the quoted prices and the market maker absorbs the excess or covers the shortfall, adjusting the prices according to the impact function (2).
|
|
(3) |
where the ε(i,f) are drawn from the normal distribution N(μ(i,f),σ(i,f)) with constant but agent-specific drift and variance. Investment funds derive their next-period orders from a value measure based on the moving average
|
|
(4) |
|
|
(5) |
|
|
(6) |
In 2.21, we will introduce VaR risk limits for the portfolios, which allow us to restrict the total exposure of investment funds to price movements in bond i.
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
where the 'tilde' denotes a random variable. Taking expectations on both sides of expression (10) then leads to the MA(m) estimate used by the SRVT to calculate the orders issued by the investment funds
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
and, after applying an error correction, we obtain the final price estimate for both bonds
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
|
|
(19) |
where μt+1 is the mean of total accumulated profits, e is a scaling factor, ηt+1 is the confidence level for the chosen strategy — see equation (22) — and b is a measure for the investor's risk aversion. In the following, we take the constant capital factor to represent the total capital available to the investor. At each trading interval the expected regret measure r allows traders to determine the amount of capital they are prepared to invest into the trading opportunity
|
|
(20) |
|
|
(21) |
and then determines the confidence level of the strategy by
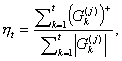
|
(22) |
where (G)+ = max(0, G).
|
|
(23) |
such that Prob{ΔV(th) < VaRη} > ηVaR. After calculating the orders θt(i,j), the time-t change of the portfolio value for agent Aj is equal to
|
|
(24) |
with ΔVt = Vt — Vt-1. Given a maximum loss limit L(j) for agent Aj, the upper bound on the time-t value of the portfolio is then
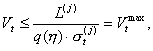
|
(25) |
where a confidence level of 99% or, equivalently, q(η) = 2.33, is used. In case condition (25) is not met, the trader will reduce the time-t orders to a level where the VaR risk limit condition is satisfied and the proportion of the bonds in the portfolio remains unchanged. Suppose now that Vt exceeds the maximum permitted portfolio value and that the difference between both values is given by δVt. Furthermore assume that time-t orders are reduced proportionally with the factor d = q(2)/q(1). It follows then that orders need to be reduced by
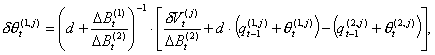
|
(26) |
|
|
(27) |
so that the portfolio satisfies the VaR risk limit. To calculate the volatility of the two-bond portfolio σ t, the historical correlation between both bonds has to be taken into account
|
|
(28) |
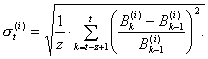
|
(29) |
The correlations are calculated using a window of the same size.
| Table 1: Parameter settings for Case 1 | |||
| Experiment | λ(1), λ(2) | NRRVT | VaR |
| E1.1 | 1.1 | 1 | no |
| E1.2 | 4 | 1 | no |
| E1.3 | 1.1 | 20 | no |
| E1.4 | 1.1 | 20 | L(j) = 0.5 |
| Table 2: Parameter settings for Case 2 | ||||
| Experiment | NRRVT | m | VaR | SRVT knows about VaR? |
| E2.1 | 1 | 1 | no | N/A |
| E2.2 | 20 | 15 | no | N/A |
| E2.3 | 20 | 15 | L(j) = 0.5 | no |
| E2.4 | 20 | 1 | L(j) = 0.5 | yes |
| E2.5 | 20 | 1 | no, L(j) = 0.5 | yes |
In each trading interval, bond prices are again set by the market maker according to the price impact function (2). Each experiment[6] consists of 200 trading intervals, except for E2.5, where profits of the SRVT are compared with those of the RRVTs over a sample of 10,000 trading rounds, each consisting again of 200 trading intervals. The initial price for both bonds is (as in Case 1) B0(i) = 10, i = 1,2, the size of the volatility window for VaR calculations is z = 25, the drifts of the exogenous value processes are drawn from the uniform distribution U(-0.03,0.03), and the volatility is equal to 0.2. All experiments have been carried out with the liquidity factors λ(1) = λ (2) = 1.1. Simulation runs have been conducted with both a constant capital factor of 1 and with a regret-dependent factor as discussed in 2.19. The scaling factor e used in the expression for the expected regret has again been set to ln(0.001)/21/2 in all experiments.
|
|
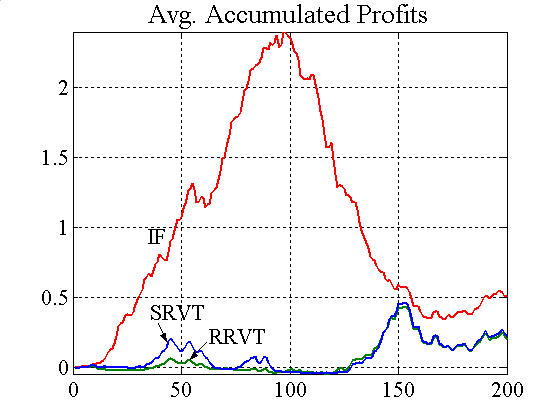
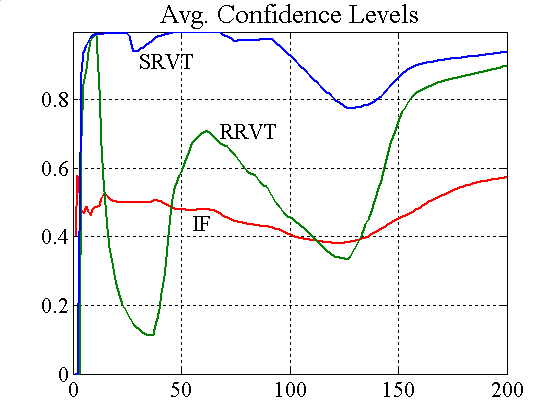
| Figure 1. Accumulated profits and confidence levels (variable capital factor)[7] |
In a market environment where investment funds outnumber RRVTs, the relative value trading strategy of either the RRVT or the SRVT shows very poor performance levels, not unlike those seen in Case 1. Since the prices follow closely the random walk of the fundamental values, there is not much room for manoeuvre for relative value traders to exploit the direction of spread movements. Figure 1 shows that the SRVT nevertheless has a slight advantage over the RRVT and that confidence levels in the higher-order strategy are well above 0.8. Hence, despite the average accumulated profits of the relative value strategy being lower than of the investment strategy, the small profit made by the SRVT is more certain. As noted above, accumulated profit graphs only show average values, and profits do change considerably from one investment fund to another. Since confidence levels of IFs are only slightly higher than 0.5, the fundamental strategy is equivalent to a zero-sum game.
|
|
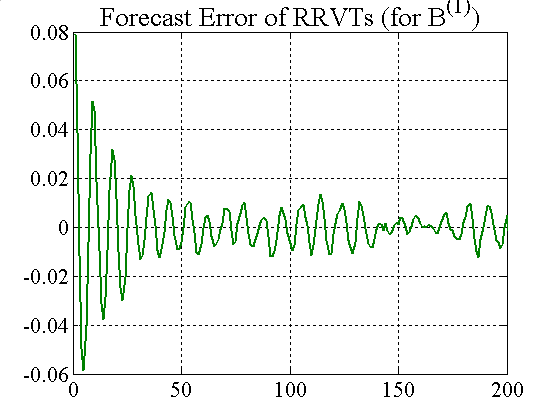
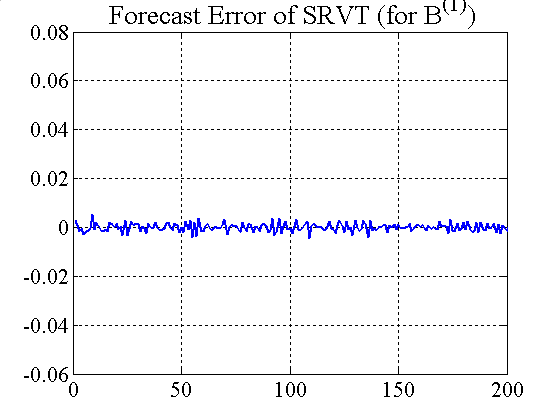
| Figure 2. Forecast error for RRVTs and SRVT (constant capital factor) |
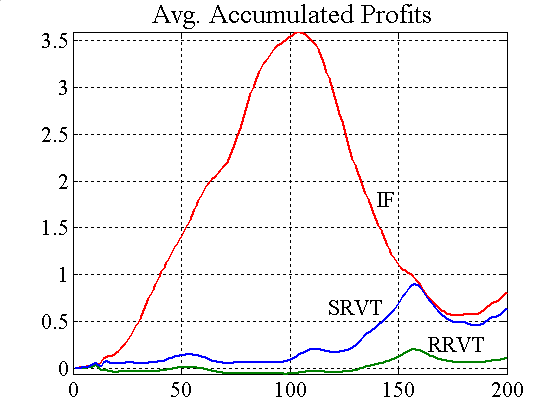
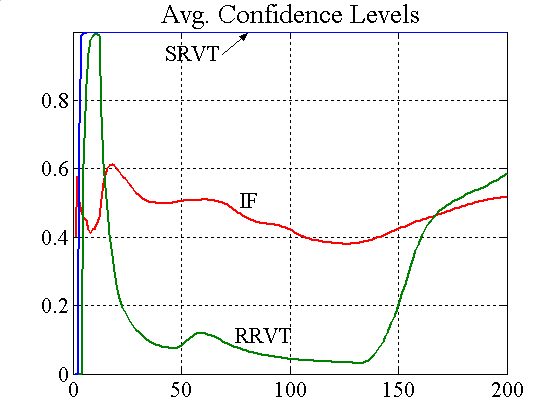
While the RRVTs do not make any substantial profit, the strategic trader does very well for both constant and variable capital factors, and the low prediction error results in steady gains, which in turn push confidence levels quickly to 1 (see figure 3). In this second case, where agents adjust their investment capital in accordance with the regret measure (19), the price behaviour becomes much less oscillatory, which is beneficial for the relative value traders, and in particular for the SRVT.
|
|
| Figure 3. Accumulated profits and confidence levels (variable capital factor) |
|
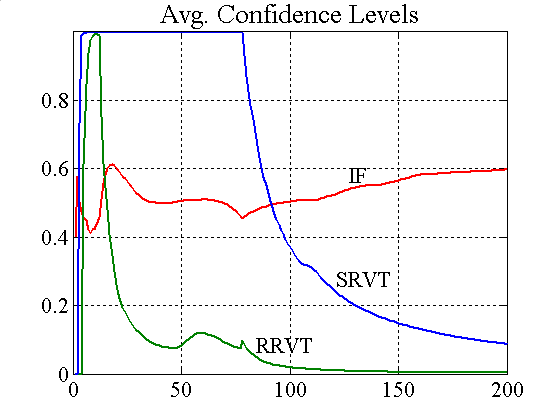
|
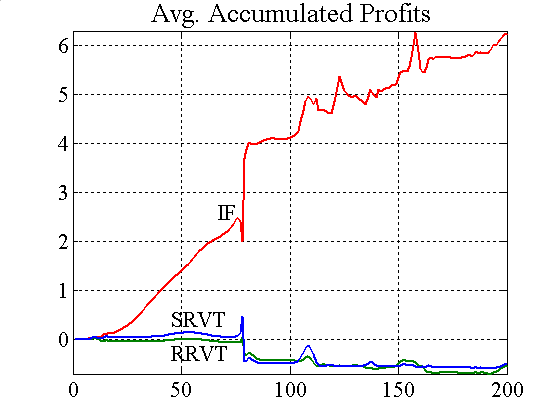
| Figure 4. Accumulated profits and confidence levels for variable capital factor (incl. VaR) |
Figure 4 shows that the SRVT strategy results in persistent losses because of the abrupt price changes caused by the investment funds' VaR position limits, even though the IFs determine the bonds' fundamental value based on a moving average (note that when the IFs used a moving average with a window of m = 15 in experiment E2.2, this had a clear benefit for the profitability of the higher-order strategy of the SRVT).
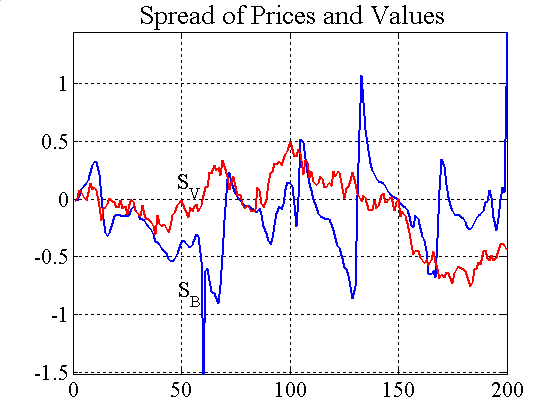
|
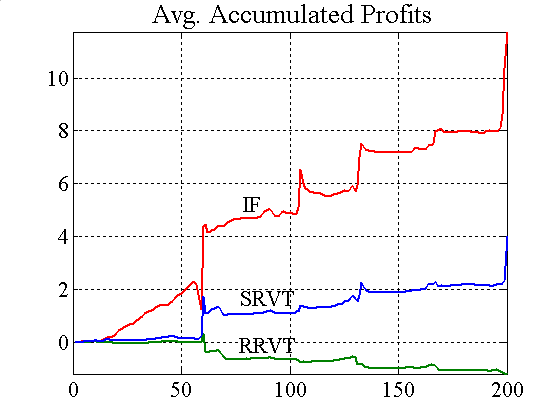
|
| Figure 5. Price spread and accumulated profits (variable capital factor) |
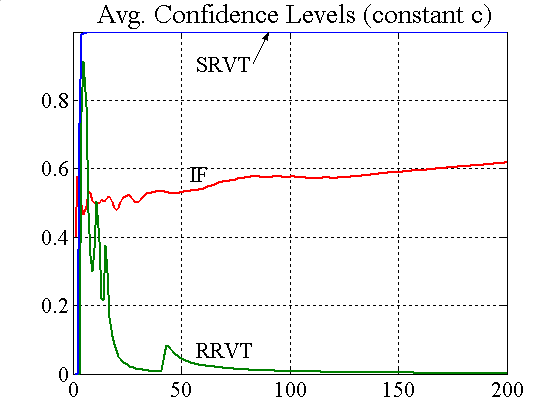
|
|
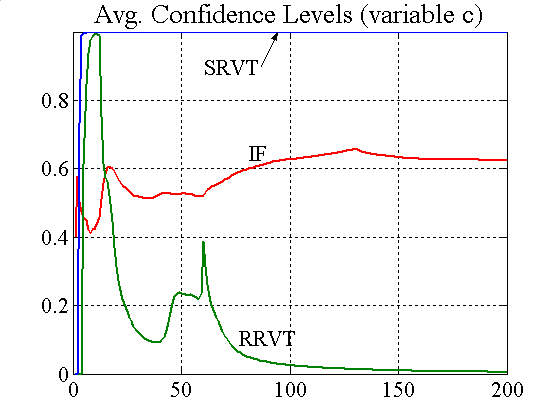
| Figure 6. Confidence levels for constant and variable capital factor |
|
|
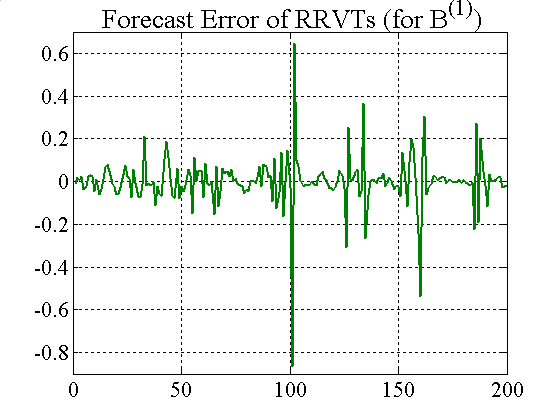
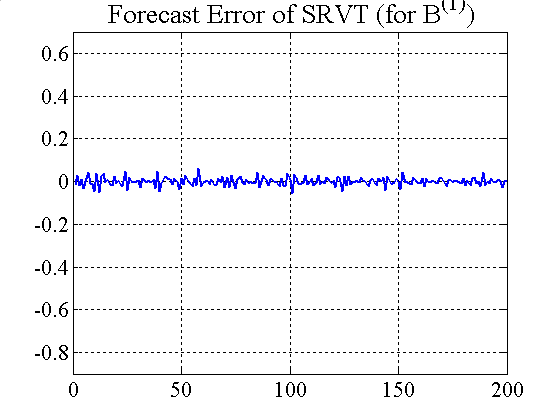
| Figure 7. Forecast error for RRVTs and SRVT (constant capital factor) |
|
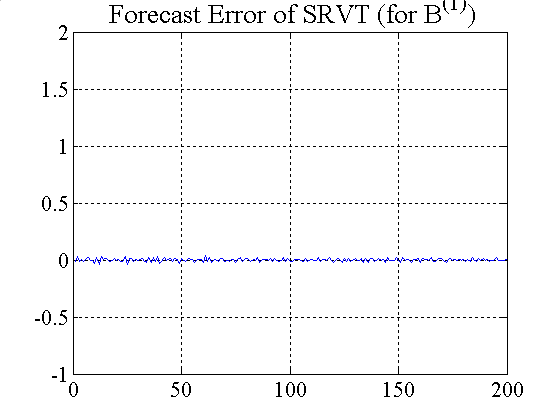
|
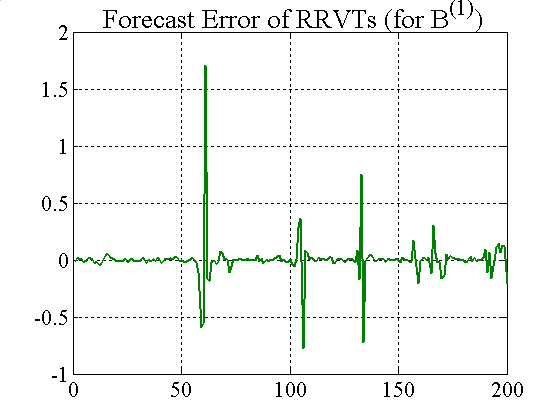
| Figure 8. Forecast error for RRVTs and SRVT (variable capital factor) |
Although the forecast errors of the RRVT are generally small when using a variable capital factor (figure 8), they become very large when the investment funds adjust their holdings according to their VaR position limits (see figure 5).
|
|
|
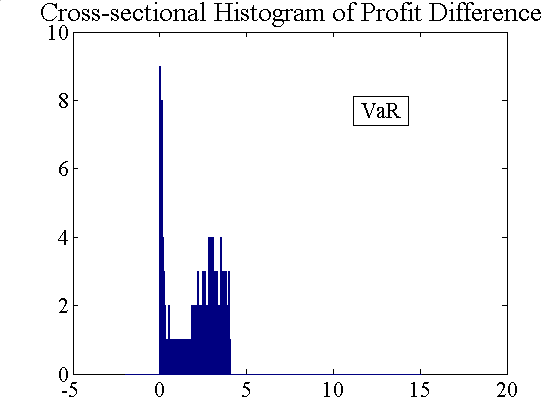
|
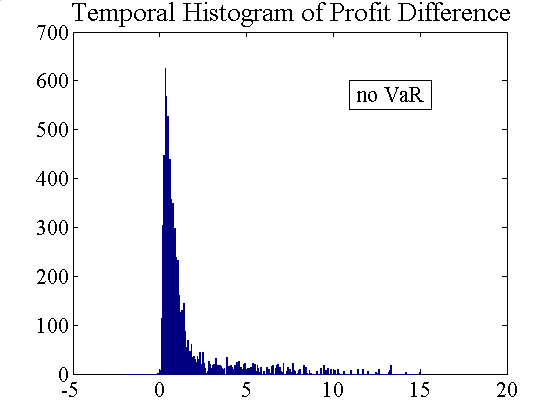
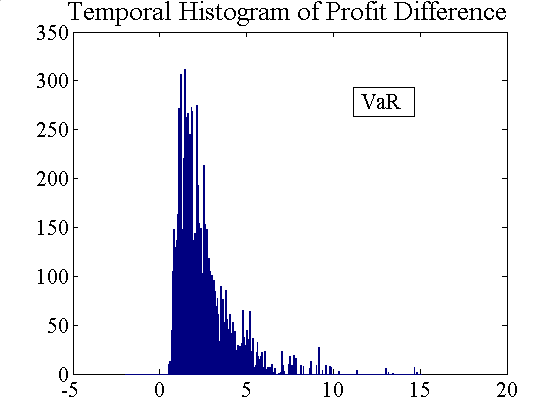
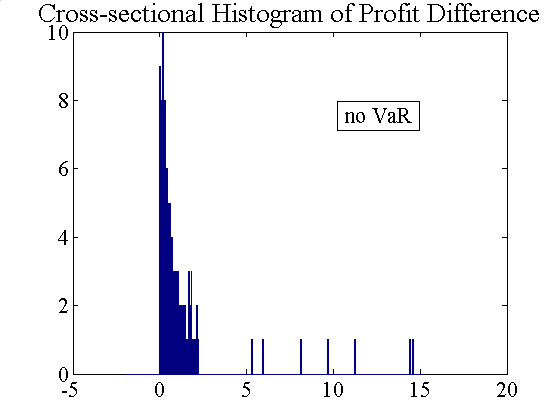
| Figure 9. Temporal and cross-sectional histograms of accumulated profit differences (left: without VaR, right: with VaR) |
2 The analogy with roulette wheels is not complete, however, since even in a perfectly competitive financial market the actions of market participants are constitutive of the outcome — the price in this case — unlike in the case of a roulette game.
3 Profit and loss
4 although the number of investment funds is equal to 20 in all experiments, we have verified that the results are robust in the range of 10-100 IFs
5 the order excess or shortfall is the sum of all orders in any given trade interval
6 Experiments E2.1 - E2.4 use the same underlying random number sequences to ensure that the results are comparable
7 the parameter values used for all figures are specified in Appendix B
8 We use the same number of investment funds throughout the cases, so as to compare the simulation results. However, we have verified that the results are robust for different numbers of IFs — from 10 to 100
9 the order excess or shortfall is the sum of all orders placed by traders at a given time
10 the parameter values used for all figures are specified in Appendix B
BIS (1999) A Review of Financial Market Events in Autumn 1998. Basel: Bank for International Settlements.
BROCK W A and Hommes C H (1998) Heterogeneous beliefs and routes to chaos in a simple asset pricing model. Journal of Economic Dynamics and Control, Vol. 22, pp. 1235-1274.
CHIARELLA C (1992) The dynamics of speculative behaviour. Annals of Operations Research, Vol. 37, pp. 101-123.
DIAMOND D W and Dybvig P H (1983) Bank runs, deposit insurance, and liquidity. Journal of Political Economy, Vol. 91 (June), pp. 401-419. Reprinted in Federal Reserve Bank of Minneapolis Quarterly Review, Vol. 24, no. 1, Winter 2000, pp. 3-13.
FARMER J D (1998) Market Force, Ecology and Evolution. Santa Fe Institute Working Paper no. 08-12-117.
HIRSHLEIFER D (2001) Investor Psychology and Asset Pricing. Journal of Finance, Vol. 56, pp.1533-1597.
HOMMES C H (2006) "Heterogeneous Agent Models in Economics and Finance." In: Tesfatsion L, and Judd K L (Eds.) Handbook of Computational Economics, Volume 2: Agent-Based Computational Economics, Amsterdam: Elsevier Science B.V.
IMF (1998) World Economic Outlook and International Capital Markets. Interim Assessment - December 1998, Washington D.C., International Monetary Fund.
KAHNEMAN D and Tversky A (2000) Choices, Values, and Frames. Cambridge: Cambridge University Press.
KIRMAN A and Teyssière G (2002) Microeconomic models for long memory in the volatility of nancial time series. Studies in Nonlinear Dynamics and Econometrics, Vol. 5, pp. 281-302.
LLACAY B and Peffer G (2004) Modelo evolutivo del impacto de técnicas VaR en los mercados financieros. Proceedings of the 7th Spanish-Italian Meeting on Financial Mathematics, Cuenca (Spain), July.
LEBARON B (2006) "Agent Based Computational Finance". In: Tesfatsion L, and Judd K L (Eds.) Handbook of Computational Economics, Volume 2: Agent-Based Computational Economics, Amsterdam: Elsevier Science B.V.
LUX T and Marchesi M (1999) Scaling and criticality in a stochastic multi-agent model of a nancial market. Nature, Vol. 397, pp. 498-500.
MACKENZIE D (2006) An Engine, not a Camera: How Financial Models shape Markets. Cambridge: MIT Press.
MACKENZIE D (2003) Long-Term Capital Management and the Sociology of Arbitrage. Economy and Society, Vol. 32, no. 3, pp. 349-380.
MADHAVAN A (2000) Market Microstructure: A Survey. Journal of Financial Markets, Vol. 3, pp. 205-258.
MANTEGNA R and Stanley H E (2000) An Introduction to Econophysics. Cambridge: Cambridge University Press.
MAYER M (1999) Risk Reduction in the New Financial Architecture. Public Policy Brief no. 56, The Jerome Levy Economics Institute of Bard College.
MORRIS S and Shin H S (2000) Market Risk with Interdependent Choice. Paper presented to the Conference on Liquidity Risk, Frankfurt (Germany), June.
MORRIS S and Shin H S (2003) "Global Games: Theory and Applications". In Dewatripont M, Hansen L and Turnovsky S (Eds.), Advances in Economics and Econometrics (Proceedings of the Eighth World Congress of the Econometric Society). Cambridge: Cambridge University Press.
SAWYER R K (2003) Artificial Societies: Multiagent Systems and the Micro-Macro Link in Sociological Theory. Sociological Methods and Research, Vol. 31, no. 3, pp. 325-363.
SHLEIFER A (2000) Inefficient Markets. Oxford: Clarendon Press.
TAKAHASHI and H Terano T (2003) Agent-Based Approach to Investors' Behavior and Asset Price Fluctuation in Financial Markets. Journal of Artificial Societies and Social Simulation, Vol. 6, no. 3. Available online on https://www.jasss.org/6/3/3.html.
| Table A1: Parameter settings for Case 1 | |||
| Experiment | λ(1), λ(2) | NRRVT | VaR |
| E1.1 | 1.1 | 1 | no |
| E1.2 | 4 | 1 | no |
| E1.3 | 1.1 | 20 | no |
| E1.4 | 1.1 | 20 | L(j) = 0.5 |
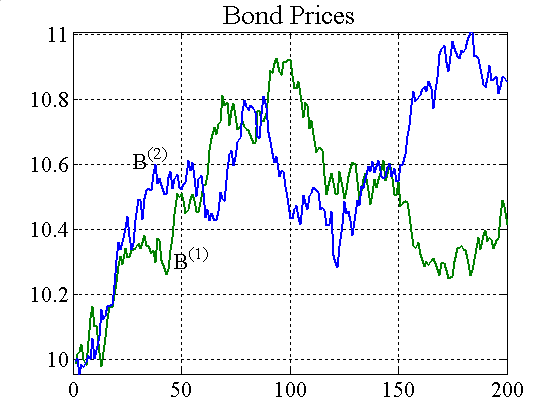
|
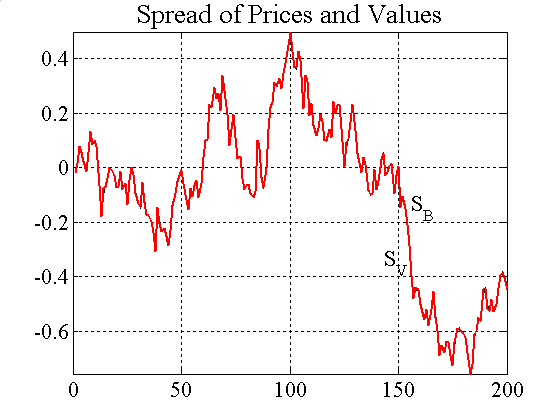
|
| Figure A1. Bond prices and price spreads for IFs and RRVTs[10] |
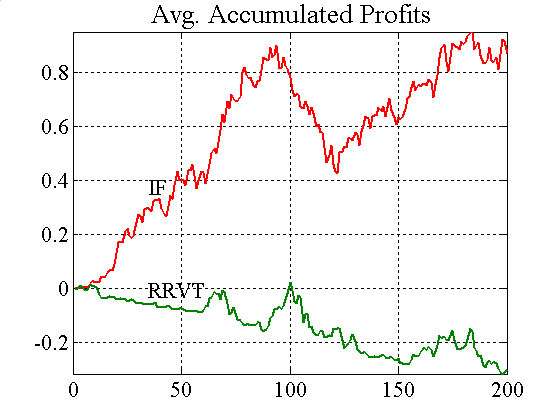
|
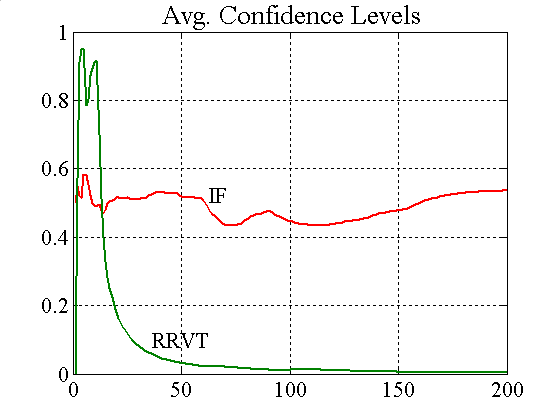
|
| Figure A2. Accumulated profits and confidence levels for IFs and RRVTs |
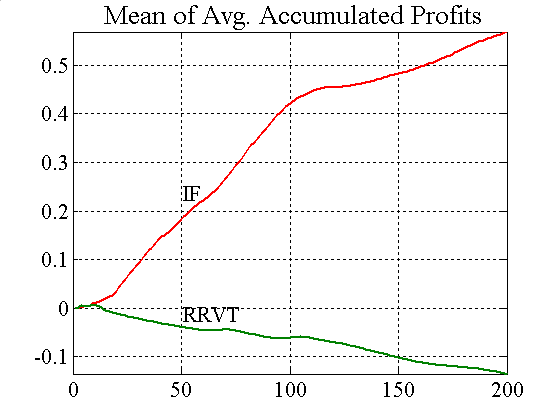
|
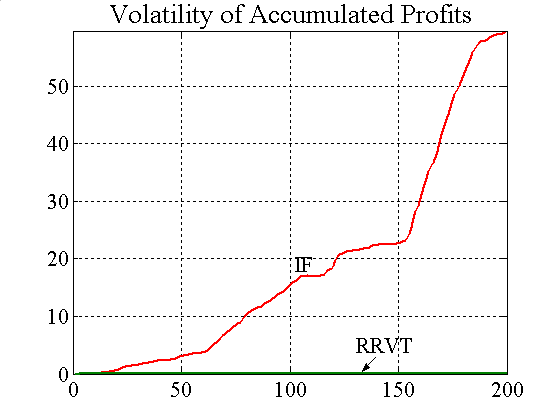
|
| Figure A3. Mean and standard deviation of accumulated profits for IFs and RRVTs |
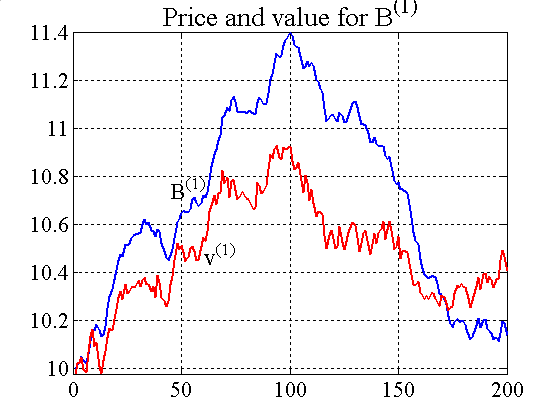
|
|
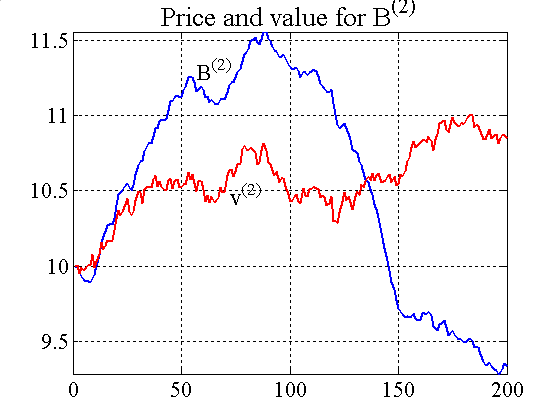
| Figure A4. Price and value process for both bonds |
|
|
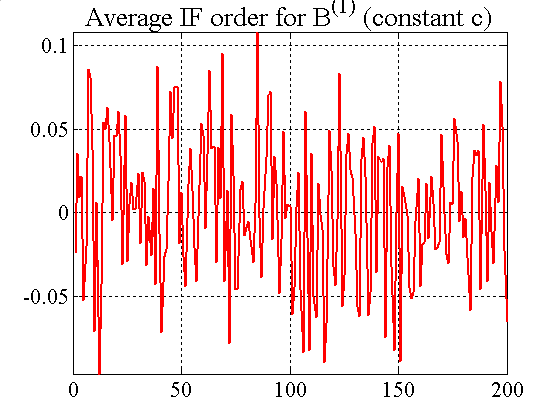
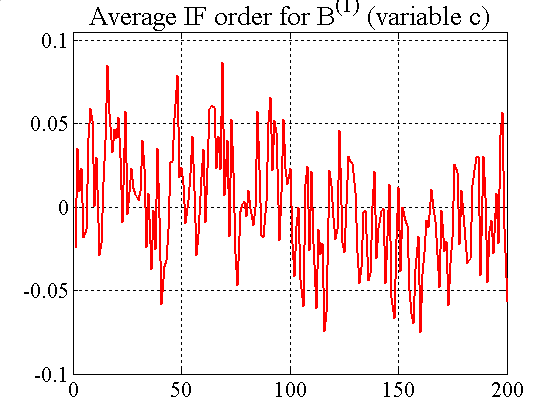
| Figure A5. Shortfall and excess order clustering for IFs |
|
|
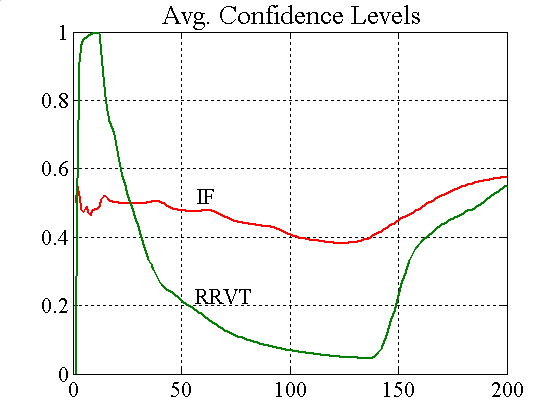
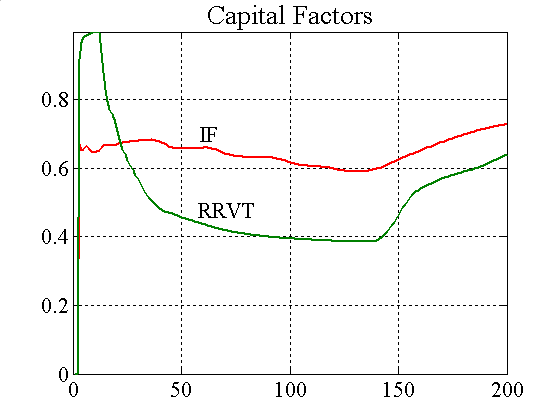
| Figure A6. Average confidence levels and capital factors for IFs and RRVTs |
|
|
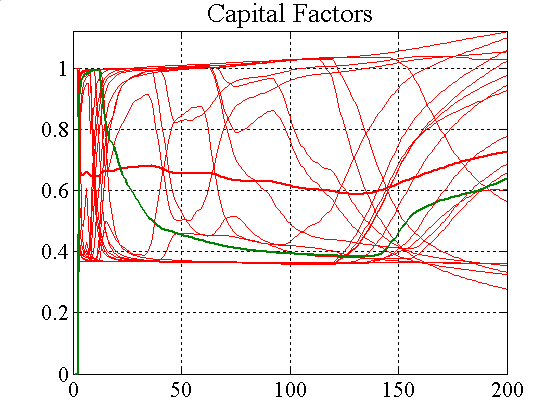
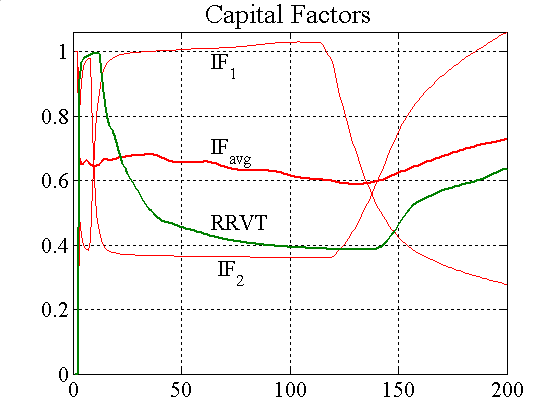
| Figure A7. IFs and RRVT capital factors and two individual paths |
|
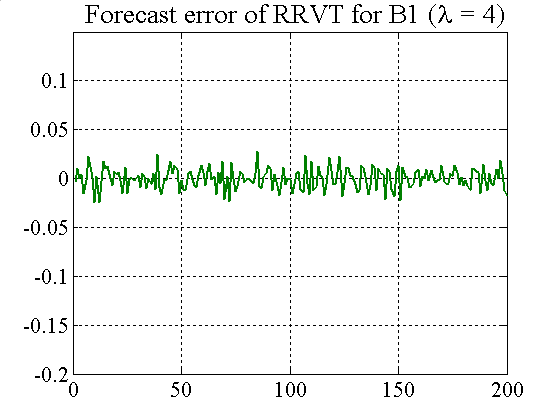
|
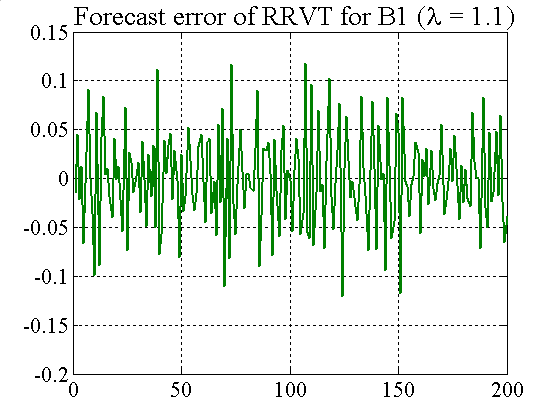
| Figure A8. Comparing forecast errors of RRVT for the two cases of λ = 1.1 and λ= 4 (constant c) |
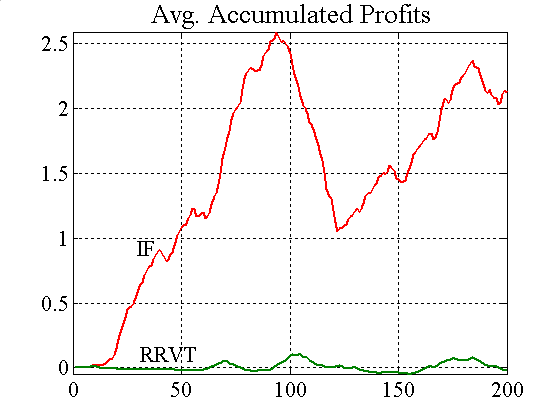
|
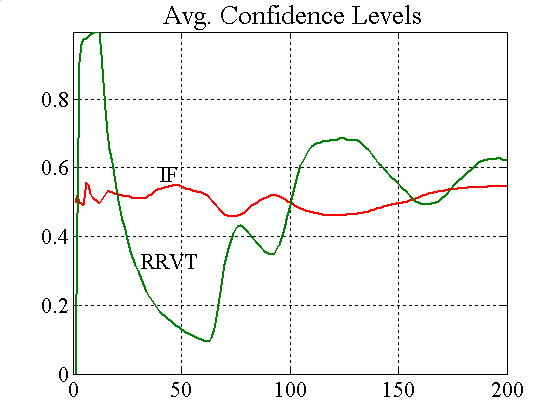
|
| Figure A9. Accumulated profits and confidence level for λ = 4 and constant capital factor |
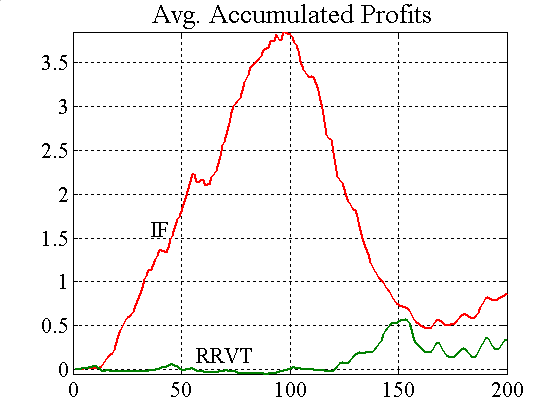
|
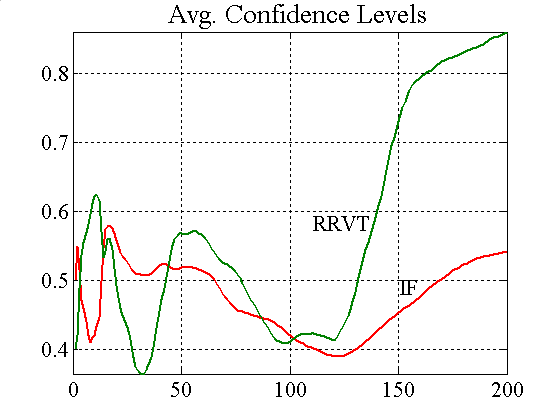
|
| Figure A10. Accumulated profits and confidence levels for variable capital factor and NRRVT =20 |
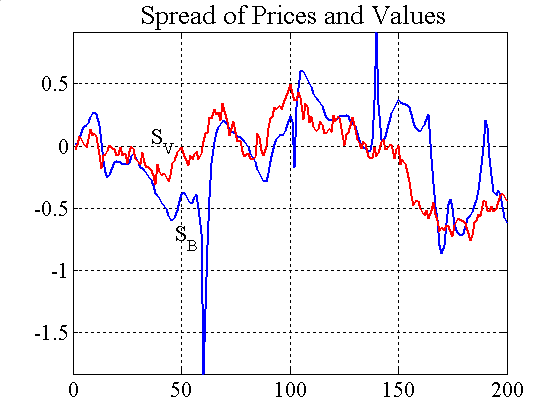
|
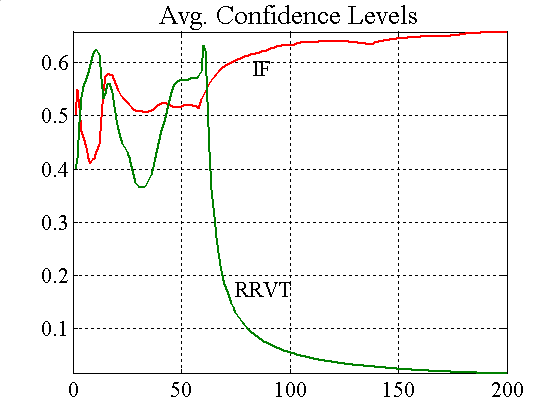
|
| Figure A11. Price spread and confidence levels when IFs use VaR |
| Table A2: Parameter Values Employed in the Figures | |||||||||||||
| Parameters | |||||||||||||
| Seed | n | B0(1), B0(2) | λ(1), λ (2) | z | m | NIF | NRRVT | NSRVT | μ(1,f), μ(2,f) | σ (1,f), σ (2,f) | c? | VaR? | |
| Fig. 1 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 1 | 1 | ~U(-0.03, 0.03) | 0.2 | variable | no |
| Fig. 2 | 21151 | 200 | 10 | 1.1 | 25 | 15 | 20 | 20 | 1 | ~U(-0.03, 0.03) | 0.2 | const. | no |
| Fig. 3 | 21151 | 200 | 10 | 1.1 | 25 | 15 | 20 | 20 | 1 | ~U(-0.03, 0.03) | 0.2 | variable | no |
| Fig. 4 | 21151 | 200 | 10 | 1.1 | 25 | 15 | 20 | 20 | 1 | ~U(-0.03, 0.03) | 0.2 | variable | L(f) = 0.5 |
| Fig. 5 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 20 | 1 | ~U(-0.03, 0.03) | 0.2 | variable | L(f) = 0.5 |
| Fig. 6 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 20 | 1 | ~U(-0.03, 0.03) | 0.2 | const. / var. | L(f) = 0.5 |
| Fig. 7 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 20 | 1 | ~U(-0.03, 0.03) | 0.2 | const. | L(f) = 0.5 |
| Fig. 8 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 20 | 1 | ~U(-0.03, 0.03) | 0.2 | variable | L(f) = 0.5 |
| Fig. 9 | N/A | 200 | 10 | 1.1 | 25 | 1 | 20 | 20 | 1 | ~U(-0.03, 0.03) | 0.2 | variable | no / L(f) = 0.5 |
| Fig. A1 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | const. | no |
| Fig. A2 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | const. | no |
| Fig. A3 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | const. | no |
| Fig. A4 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | variable | no |
| Fig. A5 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | const. / var. | no |
| Fig. A6 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | variable | no |
| Fig. A7 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | variable | no |
| Fig. A8 | 21151 | 200 | 10 | 1.1, 4 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | const. | no |
| Fig. A9 | 21151 | 200 | 10 | 4 | 25 | 1 | 20 | 1 | 0 | ~U(-0.03, 0.03) | 0.2 | const. | no |
| Fig. A10 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 20 | 0 | ~U(-0.03, 0.03) | 0.2 | variable | no |
| Fig. A11 | 21151 | 200 | 10 | 1.1 | 25 | 1 | 20 | 20 | 0 | ~U(-0.03, 0.03) | 0.2 | variable | L(f) = 0.5 |
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2007]