David Hales (1998)
Journal of Artificial Societies and Social Simulation vol. 1, no. 4, <https://www.jasss.org/1/4/2.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 27-Aug-98 Accepted: 24-Sep-98 Published: 15-Oct-98
 Abstract
Abstract
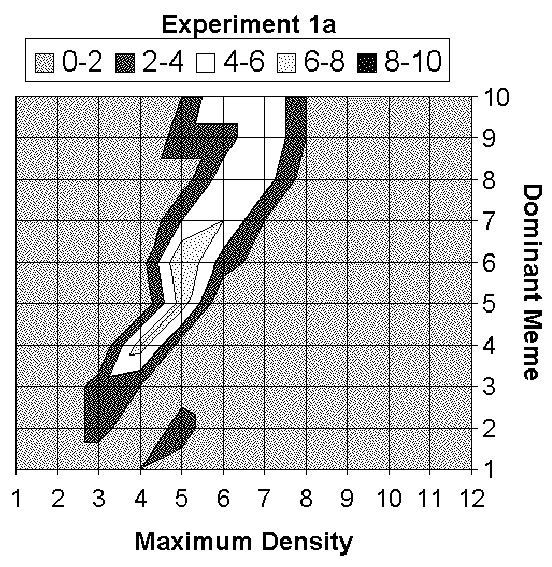 |
| Figure 1. Dominant meme / Maximum density synthesis |
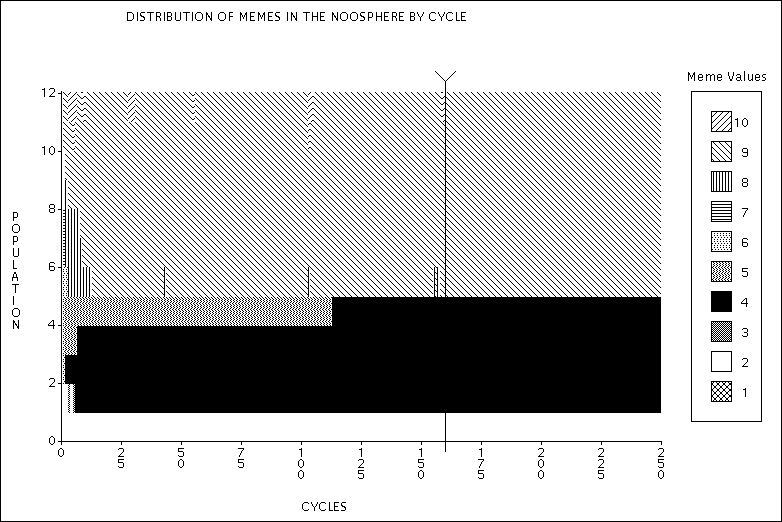 |
| Figure 2. Distribution of memes in the noosphere. Experiment 1a - Just enough food. |
| Equilibrium is reached at cycle 160. The single black line through the graph indicates this point (just after the elimination of the single "10" meme). At the start of the run the "9" meme quickly takes over the whole of a territory. The "5" meme manages to hold out for over 100 cycles before it is replaced by the "4" meme (dominant in its territory). |
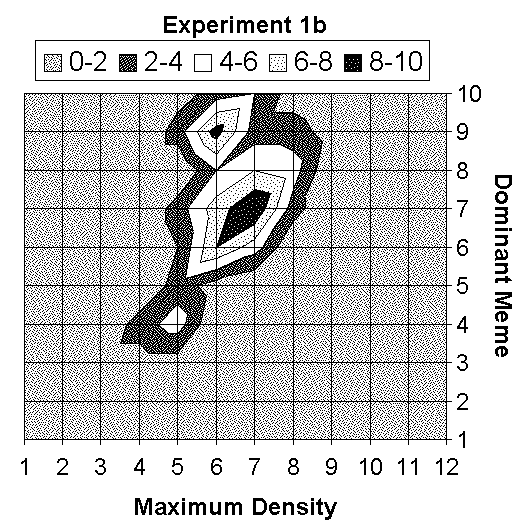 |
| Figure 3. Dominant meme / Maximum density synthesis |
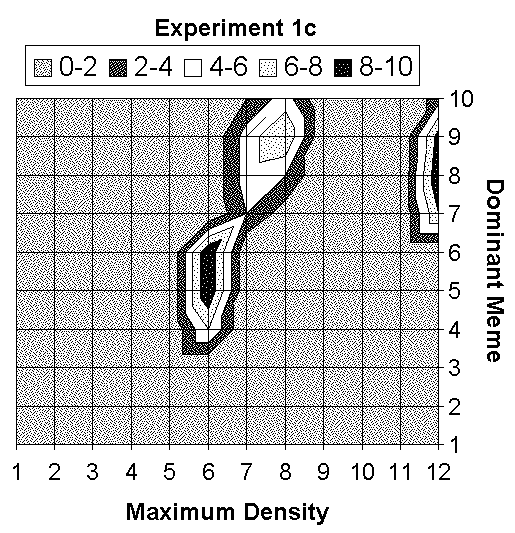 |
| Figure 4. Dominant meme / Maximum density synthesis |
The instinct for survival is important to culture because a meme, in order to be invented or acquired must pass a severe test: If it in any way endangers the lives of the animals concerned, it will automatically be rejected. (Bonner 1980, p197)
| Table 1. Meta-meme values and biases | ||||||||||
| Meta-meme | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Bias value | -1.0 | -0.8 | -0.6 | -0.4 | -0.2 | 0.0 | +0.2 | +0.4 | +0.6 | +0.8 |
| Each meta-meme value is shown along with the bias it produces. This value is added to the change parameter of each meme held by the agent when an attempted infection is taking place. Note that meta-meme value "6" has a zero bias. This means that a grazer possessing a "6" meta-meme will behave in exactly the same way as a grazer with no meta-meme at all. | ||||||||||
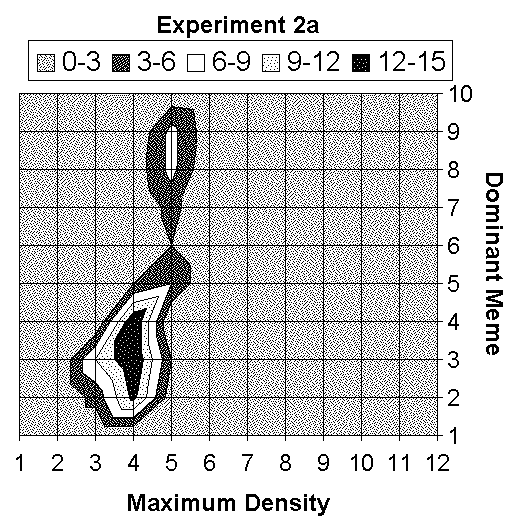 |
| Figure 5. Dominant meme / Maximum density synthesis |
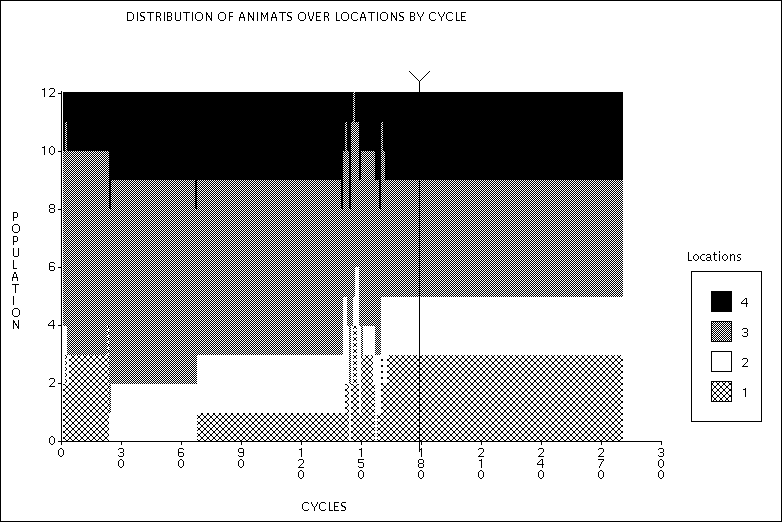 |
| Figure 6. Distribution of the population over the four territories. Experiment 2a - Just enough food. |
| Notice the redistribution of the population between cycles 140 and 160. |
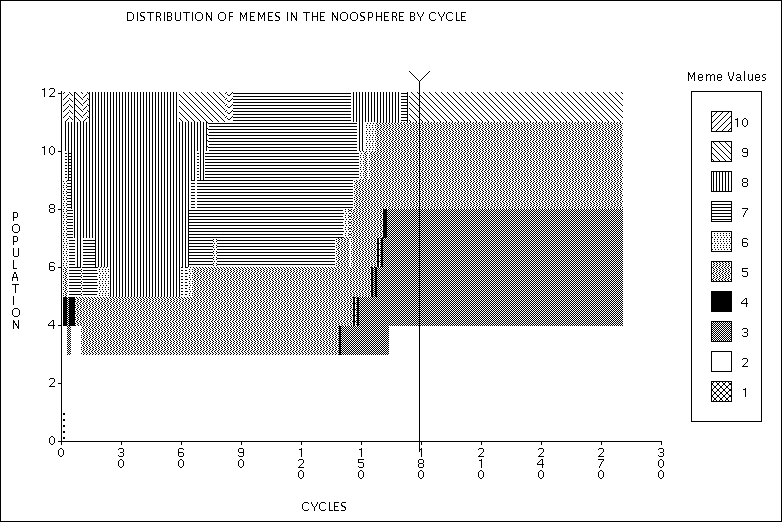 |
| Figure 7. Distribution of memes in the noosphere. Experiment 2a - Just enough food. |
| Notice the self-catalytic process and when it breaks down. |
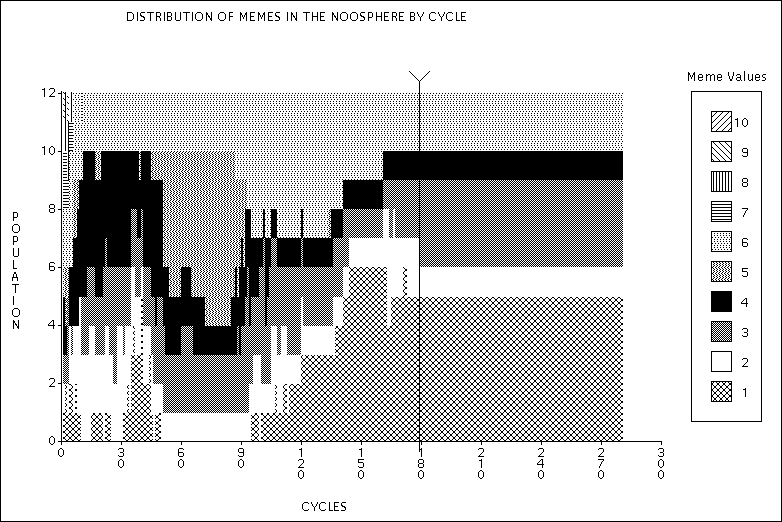 |
| Figure 8. Distribution of memes in the noosphere. Experiment 2a - Just enough food. |
| Notice the oscillations and then the minor stability between cycles 140 and 160. |
 |
| Figure 9. Dominant meme / Maximum density synthesis |
 |
| Figure 10. Dominant meme / Maximum density synthesis |
| Table 2. A summary of results | ||||||||||
| Simulation Description | 0.3 | 1 | 3 | 5 | 10 | CBE | CAE | |||
| ......Experiments without meta-memes | ||||||||||
| 1a) Just enough food | 49 | 76 | 97 | 100 | 100 | 296 | 18 | |||
| 1b) Too much food | 92 | 100 | 100 | 100 | 100 | 22 | 9 | |||
| 1c) Too much food & predators | 67 | 92 | 100 | 100 | 100 | 349 | 41 | |||
| Averages | 69 | 89 | 99 | 100 | 100 | 222 | 23 | |||
| ......Experiments with meta-memes | ||||||||||
| 2a) Just enough food | 26 | 76 | 99 | 99 | 100 | 173 | 2 | |||
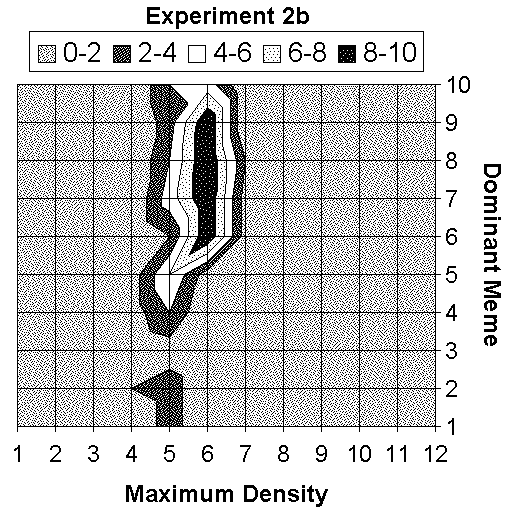
| 2b) Too much food | 62 | 97 | 100 | 100 | 100 | 32 | 2 | |||
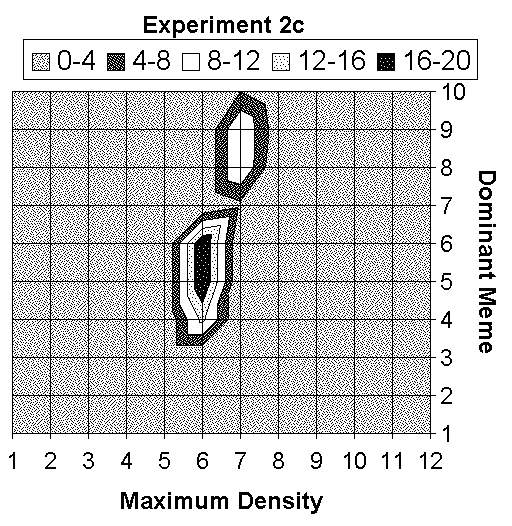
| 2c) Too much food & predators | 19 | 49 | 85 | 95 | 100 | 690 | 7 | |||
| Averages | 33 | 73 | 95 | 98 | 100 | 298 | 4 | |||
| The numbered columns represent cycles (in thousands). The numbers in those columns represent the percentage of simulation runs that had reached an equilibrium by the given number of cycles. The CBE column shows the average Cumulative deaths Before Equilibrium. The CAE column shows the average Cumulative deaths After Equilibrium. After each set of three experiments the average of the columns is given. | ||||||||||
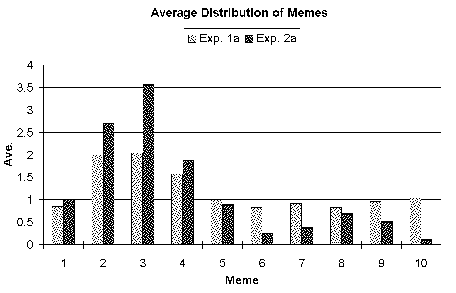 |
| Figure 11a. Distribution of memes averaged over all the simulation runs for scenario A: "Just enough food". |
| The darker bars show the results of the meta-meme experiments. After the introduction of meta-memes, meme "3" representing the actual carrying capacity is favoured. Consequently the average accuracy of the memes is improved. |
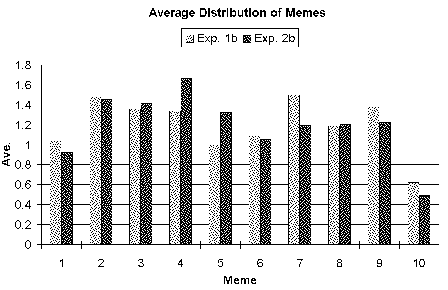 |
| Figure 11b. Distribution of memes averaged over all the simulation runs for scenario B: "Too much food". |
| The darker bars show the results of the meta-meme experiments. After the introduction of meta-memes, meme "4" representing the actual carrying capacity is favoured. Consequently the average accuracy of the memes is improved. |
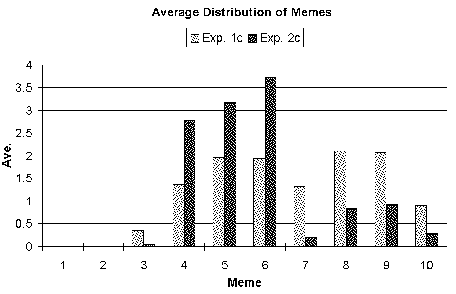 |
| Figure 11c. Distribution of memes averaged over all the simulation runs for scenario C: "Too much food with predators". |
| The darker bars show the results of the meta-meme experiments. After the introduction of meta-memes, lower value memes are favoured. Consequently the average accuracy of the memes is improved. |
bias = (m - 6) * 0.2
This formula was used because it delivers uniform increments, a neutral bias (meta-meme "6" = zero bias) and a fully closed minded meta-meme (meta-meme "1" = -1 bias).
AXELROD, R. (1997). Advancing the Art of Simulation in the Social Sciences. In Conte, R., Hegselmann, R. & Terna P. (Eds.) Simulating Social Phenomena. Berlin: Springer.
BONNER, J.T. (1980). The Evolution of Culture in Animals. New Jersey: Princeton University Press.
BOYD, R. & Richerson P. (1985). Culture and the Evolutionary Process. Chicago: University of Chicago Press.
BULLOCK, A. (ed.) (1988). Fontana Dictionary of Modern Thought. London: Fontana Press.
BURA, S. (1994). Minimeme: Of Life and Death in the Noosphere. In J. Mayer & S. Wilson (eds.) From Animals to Animats 3: Proceedings of the 3rd International Conference on the Simulation of Adaptive Behaviour (SAB94). London: MIT Press.
CONTE, R. & Gilbert, N. (1995). Introduction: Computer Simulation for Social Theory. In Gilbert, N. & Conte, R. (Eds.) Artificial Societes: the Computer Simulation of Social Life. London: UCL Press.
CONTE, R. et al (1997). Social Simulation - A New Disciplinary Synthesis. In Conte, R., Hegselmann, R. & Terna P. (Eds.) Simulating Social Phenomena. Berlin: Springer.
DAWKINS, R. (1976). The Selfish Gene. New York: Oxford University Press.
DAWKINS, R. (1982). The Extended Phenotype. Oxford: Freeman. pp97 - 117.
DAWKINS, R. (1993). Viruses of the Mind. In B. Dahlbom. (ed.) Dennett and His Critics. Cambridge: Blackwell.
DENNETT, D. (1995). Darwin's Dangerous Idea. New York: Simon & Schuster.
DORAN, J. (1994), Modelling Collective Belief and Misbelief. In M. Keane, P. Cunningham, M. Brady, & R. Byrne, (eds.) Proceedings of the Seventh Annual Conference on AI and Cognitive Science (AICS94). Dublin: Dublin University Press.
DORAN, J. (1998), Simulating Collective Belief and Misbelief. In the Journal of Artificial Societes and Social Simulation vol. 1, no.1, https://www.jasss.org/1/1/3.html
DORAN, J. & Gilbert, N. (1994), Simulating Societies: an Introduction In Gilbert, N. & Doran, J. (Eds.) Simulating Societes: The Computer Simulation of Social Phenomena. London: UCL Press.
EPSTEIN, J.M. and Axtell, R. (1996). Growing Artificial Societies: Social Science From The Bottom Up. London: MIT Press.
GABORA, L.M. (1995) Meme and Variation: A Computational Model of Cultural Evolution. In Nadel, L. & Stein, D. (Eds.) 1993 Lectures in Complex Systems. New York: Addison-Wessley.
GABORA, L.M. (1997) The Origin and Evolution of Culture and Creativity. In Journal of Memetics - Evolutionary Models of Information Transmmission vol.1, no.1, http://www.cpm.mmu.ac.uk/jom-emit/1997/vol1/gabora_l.html
HALES, D. (1995). Modelling Meta-Memes. Unpublished MSc Dissertation. Department Of Computer Science, University Of Essex, UK.
HALES, D. (1997). Modelling Meta-Memes. In Conte, R., Hegselmann, R. & Terna P. (Eds.) Simulating Social Phenomena. Berlin: Springer.
HALES, D. (1998a). Artificial Societies, Theory Building and "Ceduction". Unpublished paper, Presented at the CRESS workshop "The Potential of Computer Simulation in the Social Sciences", January 1988, University of Surrey, UK.
HALES, D. (1998b). Selfish Memes and Selfless Agents: Altruism in the Swap Shop. In The Proceedings of ICMAS 1998 (ICMAS'98). California: IEEE Computer Society.
HALES, D. (1998c). Stereotyping, Groups and Cultural Evolution. In Proceedings of the Multi-Agent Based Simulation Workshop 1998 (MABS'98) To be published by Springer in the LNAI series late 1998.
HALES, D. (1998d). Artificial Societies, Theory Building and Memetics. In Proceedings of the 15th International Congress on Cybernetics. Namur: Int. Association for Cybernetics.
HEGSELMANN, R. (1996). Cellular Automata in the Social Sciences: Perspectives, Restrictions and Artefacts. In R. Hegselmann, U. Mueller & K.G. Troitzsch (eds.) Modelling and simulation in the social sciences from a philosophy of science point of view [Theory and Decision Library]. Dordrecht: Kluver.
MATHEWS, R. (1995). It's a Lottery. New Scientist 1987, 38-42.
PRESS, H., Flannery, B., Teukolsky, S., Vetterling, W. (1992). Numerical Recipes in C : The Art Of Scientific Computing. Cambridge: Cambridge University Press.
REYNOLDS, R. (1994). Learning to Co-operate using Cultural Algorithms. In Gilbert, N. & Doran, J. (Eds.) Simulating Societies: The Computer Simulation of Social Phenomena. London: UCL Press.
SIMON, H. (1990). A Mechanism for Social Selection and Successful Altruism. Science 250: 1665-1668
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1998