Rainer Hegselmann and Andreas Flache (1998)
Journal of Artificial Societies and Social Simulation vol. 1, no. 3, <https://www.jasss.org/1/3/1.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 28-May-98 Accepted: 11-Jun-98 Published: 30-Jun-98
 Abstract
Abstract
 |
 |
|
Figure 1: Two-dimensional CA. Left: without edges pasted. Right: with edges pasted. |
|
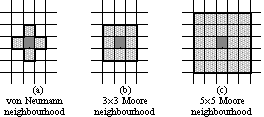 |
| Figure 2: Different neighbourhood templates. |
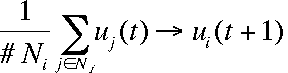 . . |
[1] |
 |
|
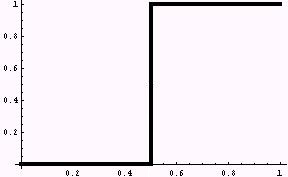
if x < 1/2, then y = 0 if x >= 1/2, then y = 1 |
 |
|
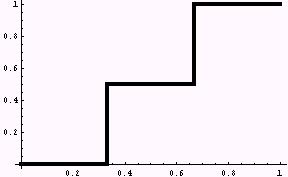
if x < 1/3, then y = 0 if x >= 1/3 and x < 2/3, then y = 0.5 if x >= 2/3, then y = 1 |
|
Figure 3. Top: two possible opinions (0 and 1). Bottom: three possible opinions (0, 0.5, and 1). |
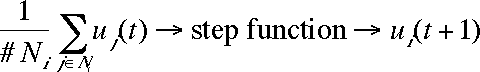 . . |
[2] |
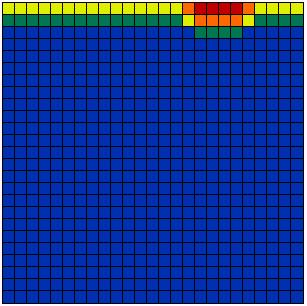
[2] is the universal transition rule. It is applied sequentially to randomly selected cells, which is to say that the updating procedure used is sequential updating. (Simultaneous updating involves simultaneously applying [2] to all cells.) Figure 4 shows the typical results of simulation runs with 2, 5, 10, 15, and 30 different opinions. At the beginning all possible opinions have the same frequency in the population. Obviously in all cases, opinion patterns and clusters emerge. The structures shown are stable for ever. In the continuous case shown in Figure 4(f), no step function is applied and the dynamics are driven by [1] instead of [2]. It can be proved analytically that these dynamics always lead to ubiquitous agreement when t tends to infinity (Hegselmann et al. 1998).

|
|
| (a) 2 possible opinions | (b) 5 possible opinions |
|
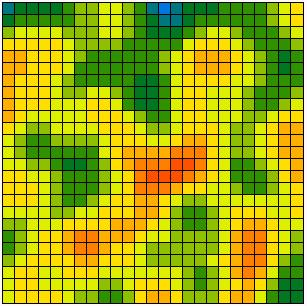
|
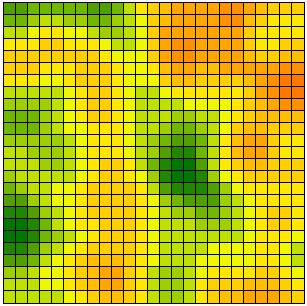
| (c) 10 possible opinions | (d) 15 possible opinions |
|

|
| (e) 30 possible opinions | (f) continuous opinions |
|
|
|
| color coding of opinions | |
| Figure 4: Results of simulation runs with 2, 5, 10, 15 or 30 discrete opinions and with continuous opinions. | |
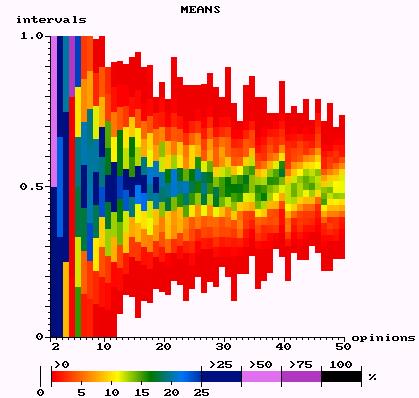 |
| Figure 5: Discrete opinion dynamics with up to 50 possible opinions: Mean frequencies of opinions after convergence. |
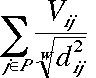 . . |
[4] |
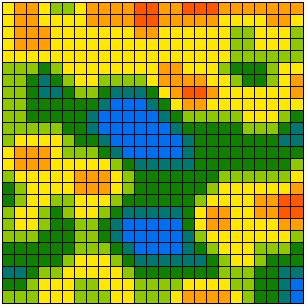
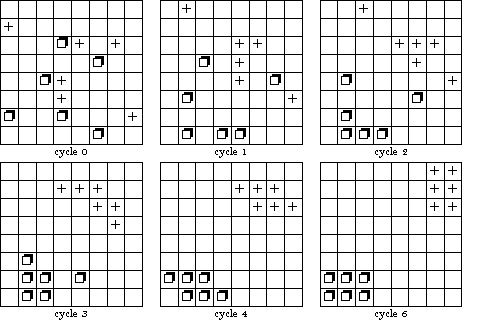
is maximised. d is the Euclidean distance between i and j. w determines how strongly valences are discounted by distance. The greater w, the less the valences are discounted by distance. Sakoda's world is an 8 × 8 checkerboard occupied by two groups, each with 6 members. The members of one group are represented as squares and members of the other as crosses. Sakoda analyses different combinations of attitudes. One of these is called segregation, another is called suspicion. These attitudes are shown in Figure 6.
 |
| Figure 6: The attitude combinations segregation and suspicion. |
 |
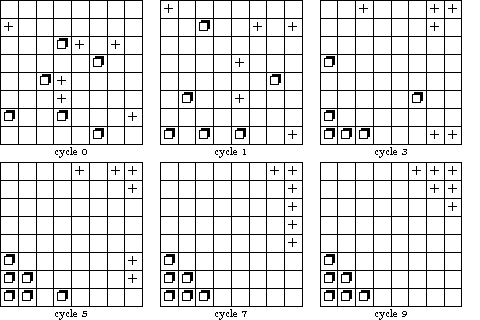
| Figure 7: The dynamics of segregation (Sakoda 1971, p. 127). |
 |
| Figure 8: The dynamics of suspicion (Sakoda 1971, p. 126). |
 |
 |
| Figure 9. Left: segregation
Right: suspicion. Both dynamics were started with the same random distribution of cells. |
|
| Figure 10. Left: random distribution (Schelling 1971, p. 155). Right: segregation (Schelling 1971, p. 157). | |
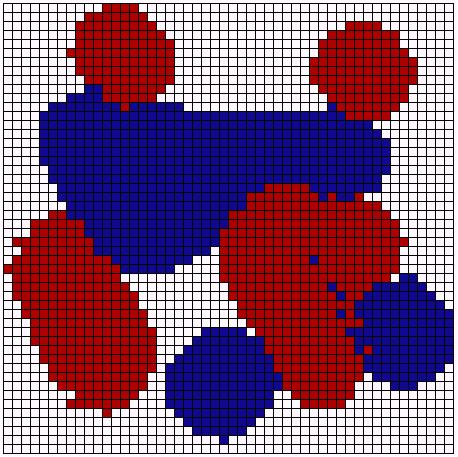 |
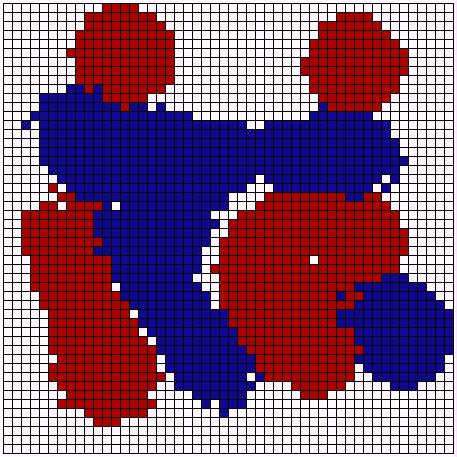 |
| Preference: <= 90% | Preference: <= 50% |
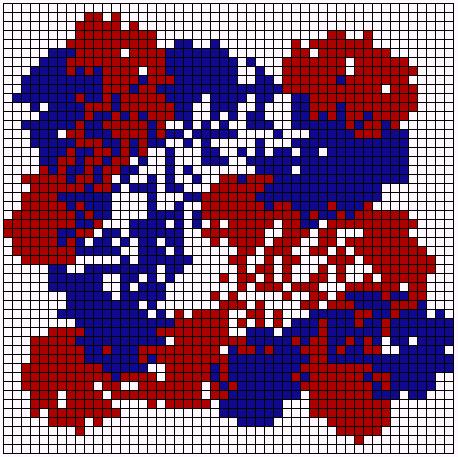 |
 |
| Preference: <= 30% | Preference: <= 20% |
| Figure 11: Experiments with different neighborhood preferences. | |
Nevertheless, it is only within the last decade that CA based models have been used more frequently in the behavioural and social sciences.[9] In social psychology, Nowak et al. (1990) have developed a two-dimensional CA model of evolution in attitudes. In economics, Keenan and O'Brien (1993) use a one-dimensional CA to model and analyse pricing in a spatial setting. Axelrod (1984, pp. 158ff.) made the first steps in analysing the dynamics of cooperation within a CA framework, although he did not refer to his model as a CA. Nowak and May (1992, 1993) developed the idea and studied the dynamics of cooperation using a two-dimensional CA with two-person games as building blocks. Bruch (1993) and Kirchkamp (1994) follow the same line, but use different and more sophisticated learning rules. The same framework is used in Messick and Liebrand (1995), who analyse the dynamics of three different decision principles.[10] A substantial number of the artificial societies described in Epstein and Axtell (1996) are based on CA modes. Gaylord and D'Andra (1998) describe a toolkit for CA based modelling of social dynamics using MATHEMATICA.
 | |||
| S : | Saved | D: Drowned | S > D |
| M: | Move on | H: Help | M > H |
| p1 : | probability that player 1 will become needy | ||
| p2: | probability that player 2 will become needy | ||
| 0 < p1, p2 < 1 | |||
| Figure 12: Support game[12] | |||
| [5] |
Provided that the condition in [5] is fulfilled the expected payoff for mutual support is greater than the expected payoff for not giving support to each other. Therefore [5] describes a condition under which the solution of the support game becomes inefficient. If characterised as a matrix game one can easily verify that [5] describes a condition under which the support game turns into a 2-person Prisoner's Dilemma. We will refer to [5] as the PD-condition.
An iterated support game has a cooperative solution if and only if, for both players, it holds that:
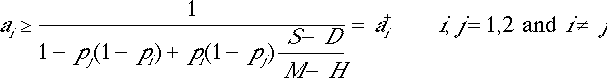 . . |
[6] |
[6] is based on the assumption that it is only in cases of unilateral emergency that one player can infer whether the other is cooperating or defecting. I will refer to [6] as the COOP-condition.[14]
Support Networks
Basics| interaction window: | von Neumann neighbourhood. |
| migration window: | 11 × 11 with the given position in the centre. |
| world: | 21 × 21 (torus). |
Class structure
individuals per risk class: 35, giving a total of 315 individuals and 136 empty sites.
Payoffs and minimum level
Saved = 5, Drowned = 1, Move on = 7 and Help = 6 so (S - D) / (M -H) = 4 and the minimum level is 50%.
Probabilities for getting migration options
| 0.05 | => | a = 0.903 (first experiment) |
| 0.10 | => | a = 0.810 (second experiment) |
| 0.15 | => | a = 0.723 (third experiment) |
Use of migration options
Figure 13: Initial conditions
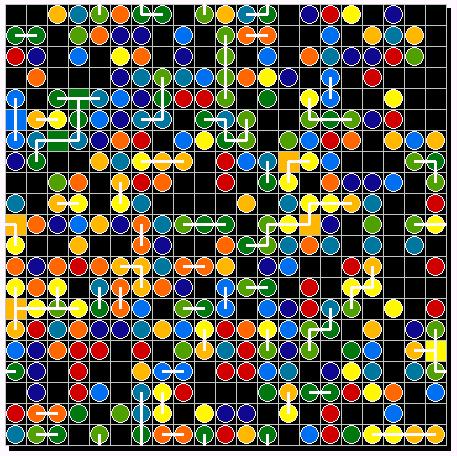
|
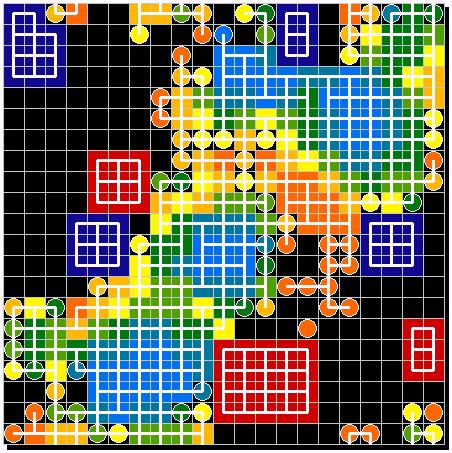
| |
| Figure 13: primordial soup | Figure 14. First experiment: chance for migration 5% | |
|
|
|
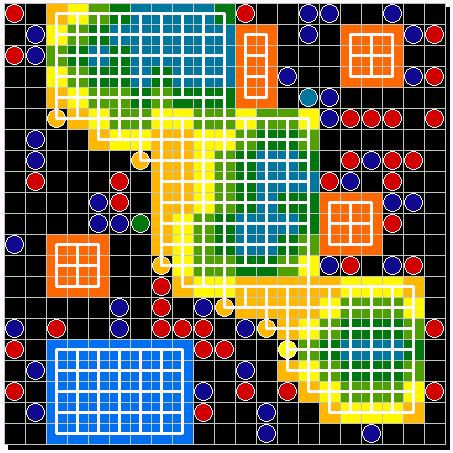
| Figure 15. Second experiment: chance for migration 10% | Figure 16. Third experiment: chance for migration 15% |
 |
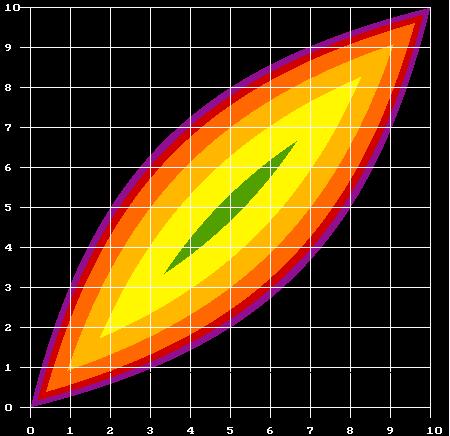
| Figure 17: PD and COOP-condition for (S-D)/(M-H) = 4. |
The last point - a direct consequence of [6] - may seem surprising at first glance. The explanation is that two individuals of extreme risk classes are facing a problem which members of intermediate classes only experience to a much lesser degree. It is very likely that two members of the least needy risk class will not need help. Two members of the most needy risk class will probably be in need of help simultaneously and thus neither of them will be in a position to help the other. In both cases, unilateral emergencies become rare events. For this reason, the expected utility of mutual support decreases at the extremes. At the same time, it becomes more difficult to find out whether other individuals are cooperating or defecting. Therefore, probabilities of stability which makes support relations effective for intermediate risk classes may not be sufficient for the extreme risk classes.
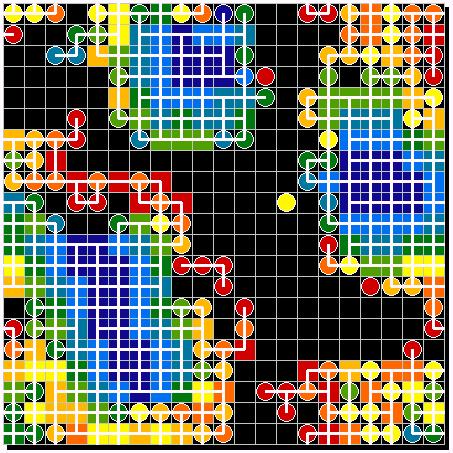
 |
 |
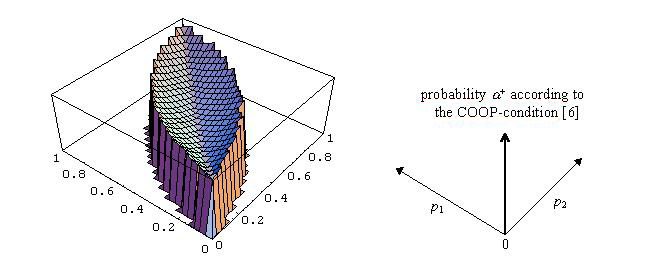
| Figure 18: The colours indicate the probability (a+) that has to be exceeded to meet the COOP-condition [6] for a given pairing of risk classes. Black indicates that the PD-condition [5] is not met for that pair of risk classes. As before (S-D)/(M-H) = 4. | |
| RISK CLASS | quite bad | middle risk | quite good |
| quite bad | COOP-condition tends not to be fulfilled. | COOP and PD-condition tend not to be fulfilled. | |
| middle risk | COOP and PD-condition can comparatively easy be fulfilled. | ||
| quite good | COOP and PD-condition tends not to be fulfilled. | COOP-condition tends not to be fulfilled. | |
| Figure 19: Problems of pairing. | |||
| [7] |
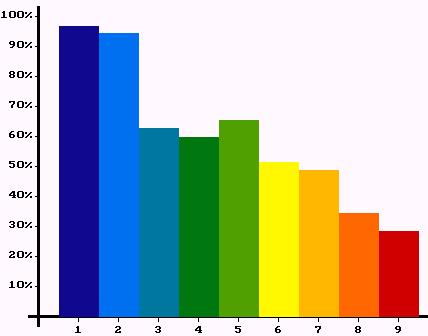 |
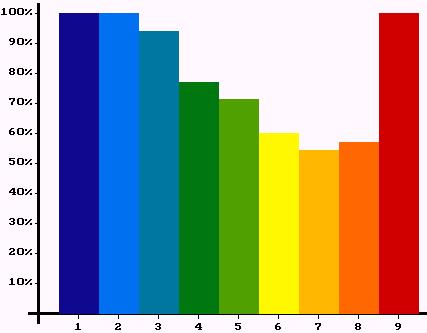 |
| Figure 20: Percentages of satisfied agents in different classes. Left: first experiment. Right: second experiment. | |
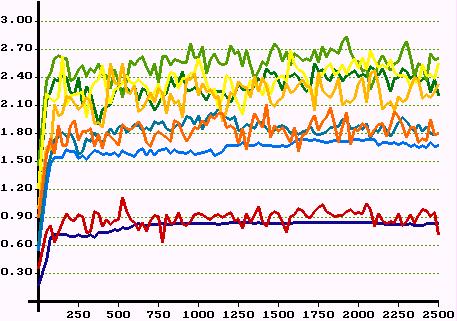 |
|
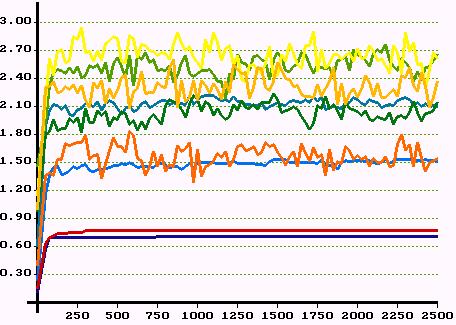 |
|
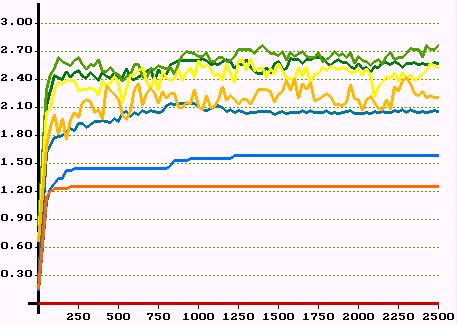 |
|
| Figure 21. Average network dividend in all classes over 2500 periods. Top: first experiment. Middle: second experiment. Bottom: third experiment. Colours indicate classes. | |
| [8] |
Obviously, the lower pi, the higher ![]() . Let
. Let ![]() be the total payoff for a member of class i in period t. Then:
be the total payoff for a member of class i in period t. Then:
| [9] |
is what a member of class i gets in period t due to successfully established support relations. Let's call ![]() the network dividend. Figure 21 shows the development of the average network dividend for all 9 classes over 2500 periods for the three experiments.
the network dividend. Figure 21 shows the development of the average network dividend for all 9 classes over 2500 periods for the three experiments.
2 The model is basically a special case of French (1956), Harary (1959) and Abelson (1964). See also Nowak et al. (1990) and Hegselmann et al. (1998).
3As states we use a finite number (n) of real valued opinions. It would be just as easy to represent opinions by integer values but this would not affect any of the arguments presented in the paper.
4Obvously, the step functions in Figure 3 are not the only method for obtaining a finite number of possible opinions from an infinite set of real valued opinions. For example, it might be more realistic to assume that a particular opinion is adopted with a probability that declines with the distance between that opinion and ui*(t+1). However, we do not investigate this possibility, because this paper focuses on illustrating the CA framework rather than demonstrating the empirical adequacy of a particular model.
5That includes the possibility of modelling and understanding micro/macro feedback loops within the CA framework.
6For a discussion of artefacts related to updating procedures see Huberman and Glance (1993) and Hegselmann (1996).
7This model plays an important role in Lehman (1977), an early introduction to computer simulations for social scientists.
8 Another early application of checker board modelling is Hägerstrand (1965) where it is used to analyse the diffusion of new agricultural techniques.
9This is due to the fact that those models ask for a great deal of iterated computation even if very simple assumptions are used. It has become progressively easier since user-friendly programming languages and powerful debugging tools have been created. Nowadays corresponding hardware and software is also available to social scientists.
10 For recent overviews of research on social dilemmas see Schulz et al. (1994) and Liebrand and Messick (1996).
11 The model was originally developed in Hegselmann (1994a, 1994b).
12 In what follows, it is always assumed that D < M. When D > M we get support games in which those in need of help are those with favourable opportunities which they cannot take advantage of without support from another actor.
13 But notice that there are also many other equilibria.
14 The proof of [6] only exists as a manuscript available from the author.
15 This implies that we can assume that the equilibrium selection problem has been solved!
16 Details will be demonstrated in another article.
17 For an analysis of different types of simulations see Hartmann (1996), Kliemt (1996) and Troitzsch (1998).
ABELSON, R P (1964) Mathematical Models of the distribution of attitudes under controversy. In: N. Frederiksen and H. Gulliken (eds.) Contributions to mathematical psychology. Holt, Rinehart and Winston: New York, NY. pp. 142-160.
ALBIN, P S (1975) The Analysis of Complex Socioeconomic Systems. Lexington Books: London.
ALBIN, P S (1998) Barriers and Bounds to Rationality: Essays on Economic Complexity and Dynamics in Interactive Systems. Princeton University Press: Princeton, NJ.
AXELROD, R (1984) The evolution of cooperation. Basic Books: New York, NY.
BRUCH, E (1993) The evolution of cooperation in neighbourhood structures. Manuscript, Bonn University.
BURKS, A W (1970) Essays on cellular automata. University of Illinois Press: Urbana, IL.
CASTI, J L (1992) Reality rules: Picturing the world in mathematics , Volume I: The Fundamentals, Volume II: The Frontier. John Wiley and Sons: New York, NY.
DEMONGEOT, J, GOLES, E and TCHUENTE, M (eds.) (1985) Dynamical systems and cellular automata. Academic Press: London.
EPSTEIN, J M and AXTELL, R (1996) Growing Artificial Societies: Social Science from the Bottom Up. MIT Press: Cambridge, MA.
FRENCH, J R P (1956) A Formal Theory of Social Power. Psychological Review 63. pp. 181-194.
FLACHE, A and HEGSELMANN, R (1997) Rational vs. adaptive egoism in support networks - How different micro foundations shape different macro hypotheses. In: Leinfellner, W and Köhler, E (eds.) Game Theory, Experience, Rationality. Kluwer: Dordrecht. pp. 261-275.
FRIEDMAN, J W (1986) Game theory with applications to economics, second edition 1991. Oxford University Press: Oxford.
GAYLORD, R J and D'ANDRA, L (1998), Simulating Society: A MATHEMATICA Toolkit for Modelling Socioeconomic Behavior. Springer: New York, NY.
GUENTHER, O, HOGG, T and HUBERMAN, B A (1997) Market organizations for Controlling Smart Matter. In: R. Conte, R. Hegselmann and P. Terna (eds.) Simulating Social Phenomena. Springer: Berlin. pp. 241-257.
GUTOWITZ, H (ed.) (1991) Cellular automata: theory and experiment. MIT Press: Cambridge, MA.
HÄGERSTRAND, T (1965) A Monte Carlo approach to diffusion. European Journal of Sociology 63. pp. 43-67.
HARARY, F (1959) A Criterion for Unanimity in French's Theory of Social Power. In: D. Cartwright (ed.) Studies in Social Power. Institute of Social Research, University of Michigan: Ann Arbor, MI. pp. 168-182.
HARTMANN, S (1996) The world as a process: Simulations in the natural and social sciences. In: R. Hegselmann, U. Mueller and K. G. Troitzsch (eds.) Modelling and simulation in the social sciences from a philosophy of science point of view . Kluwer: Dordrecht. pp. 77-100.
HEGSELMANN, R (1994a) Zur Selbstorganisation von Solidarnetzwerken unter Ungleichen - Ein Simulationsmodell. In: K. Homann (ed.) Wirtschaftsethische Perspektiven I - Theorie, Ordnungsfragen, Internationale Institutuionen. Duncker and Humblot: Berlin. pp. 105-129.
HEGSELMANN, R (1994b) Solidarität in einer egoistischen Welt - Eine Simulation. In: J. Nida-Rümelin (ed.) Praktische Rationalität - Grundlagen und ethische Anwendungen des rational choice-Paradigmas. Walter de Gruyter: Berlin. pp. 349-390.
HEGSELMANN, R (1996) Cellular automata in the social sciences: Perspectives, restrictions and artefacts. In: R. Hegselmann, U. Mueller and K. G. Troitzsch (eds.) Modelling and simulation in the social sciences from a philosophy of science point of view . Kluwer: Dordrecht. pp. 209-234.
HEGSELMANN, R, FLACHE, A and MÖLLER, V (1998) Solidarity and Social Impact in Cellular Worlds - Results and Sensitivity Analyses. In: R. Suleiman, K. G. Troitzsch and N. Gilbert (eds.) Social Science Microsimulation: Tools for Modeling, Parameter Optimization and Sensitivity Analysis. Springer: Berlin 1998, to appear.
HUBERMAN, B A and GLANCE, N S (1993) Evolutionary Games and Computer Simulations. Proceedings of the National Academy of Science 90. pp. 7716-7718.
KEENAN, D C and O'BRIEN, M J (1993) Competition, Collusion, and Chaos. Journal of Economic Dynamics and Control 17. pp. 327-353.
KIRCHKAMP, O (1994) Spatial evolution of automata in the prisoners' dilemma. Manuscript, Bonn University.
KLIEMT, H (1996) Simulation and rational practice. In: R. Hegselmann, U. Mueller and K. G. Troitzsch (eds.) Modelling and simulation in the social sciences from a philosophy of science point of view . Kluwer: Dordrecht. pp. 13-28.
LEHMAN, R S (1977) Computer simulation and modeling: An introduction. Lawrence Erlbaum Associations: Hillsdale, NJ.
LIEBRAND, W B G and MESSICK, D (eds.) (1996) Frontiers in Social Dilemmas Research. Springer: New York, NY.
MESSICK, D M and LIEBRAND, W B G (1995) Individual heuristics and the dynamics of cooperation in large groups. Psychological Review 102. pp. 131-145.
NEUMANN, J von (1966) Theory of self-reproducing automata , edited and completed by Arthur W. Burks. University of Illinois Press: Urbana, IL.
NOWAK, A, SZAMREZ, J and LATANÉ, B (1990) From private attitude to public opinion - Dynamic theory of social impact.Psychological Review 97. pp. 362-376.
NOWAK, M A and MAY, R M (1992) Evolutionary games and spatial chaos. Nature 359. pp. 826-829.
NOWAK, M A and MAY, R M (1993) The spatial dilemmas of evolution. International Journal of Bifurcation and Chaos 3. pp. 35-78.
SAKODA, J M (1949) Minidoka: An analysis of changing patterns of social interaction. Unpublished doctoral dissertation, University of California: Berkeley.
SAKODA, J M (1971) The checkerboard model of social interaction. Journal of Mathematical Sociology 1. pp. 119-132.
SCHELLING, T (1969) Models of segregation. American Economic Review 59. pp. 488-493.
SCHELLING, T (1971) Dynamic models of segregation. Journal of Mathematical Sociology 1. pp. 143-186.
SCHULZ, U, ALBERS, W and MUELLER, U (eds.) (1994) Social Dilemmas and Cooperation. Springer: Berlin.
TAYLOR, M (1987) The possibility of cooperation . John Wiley and Sons, London.
TOFFOLI, T and MARGOLUS, N (1987) Cellular automata machines: A new environment for modeling. MIT Press: Cambridge, MA.
TROITZSCH, K G (1998) Multilevel modeling in the social sciences - Mathematical analysis and computer simulation. In: W. B. G. Liebrand, A. Nowak and R. Hegselmann (eds.) Computer Modeling of Social Processes. Sage: London.
WOLFRAM, S (1984) Universality and complexity in cellular automata. Physica D. 10. pp. 1-35.
WOLFRAM, S (ed.) (1986) Theory and applications of cellular automata. World Scientific: Singapore.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1998