István Back and Andreas Flache (2006)
The Viability of Cooperation Based on Interpersonal Commitment
Journal of Artificial Societies and Social Simulation
vol. 9, no. 1
<https://www.jasss.org/9/1/12.html>
For information about citing this article, click here
Received: 20-Jul-2005 Accepted: 25-Sep-2005 Published: 31-Jan-2006
 Abstract
AbstractA prominent explanation of cooperation in repeated exchange is reciprocity (e.g. Axelrod 1984). However, empirical studies indicate that exchange partners are often much less intent on keeping the books balanced than Axelrod suggested. In particular, there is evidence for commitment behavior, indicating that people tend to build long-term cooperative relationships characterised by largely unconditional cooperation, and are inclined to hold on to them even when this appears to contradict self-interest.
Using an agent-based computational model, we examine whether in a competitive environment commitment can be a more successful strategy than reciprocity. We move beyond previous computational models by proposing a method that allows to systematically explore an infinite space of possible exchange strategies. We use this method to carry out two sets of simulation experiments designed to assess the viability of commitment against a large set of potential competitors. In the first experiment, we find that although unconditional cooperation makes strategies vulnerable to exploitation, a strategy of commitment benefits more from being more unconditionally cooperative. The second experiment shows that tolerance improves the performance of reciprocity strategies but does not make them more successful than commitment.
To explicate the underlying mechanism, we also study the spontaneous formation of exchange network structures in the simulated populations. It turns out that commitment strategies benefit from efficient networking: they spontaneously create a structure of exchange relations that ensures efficient division of labor. The problem with stricter reciprocity strategies is that they tend to spread interaction requests randomly across the population, to keep relations in balance. During times of great scarcity of exchange partners this structure is inefficient because it generates overlapping personal networks so that often too many people try to interact with the same partner at the same time.
Perhaps the strongest evidence that friendships are based on commitment and not reciprocity is the revulsion people feel on discovering that an apparent friend is calculating the benefits of acting in one way or another. People intuitively recognize that such calculators are not friends at all, but exchangers of favors at best, and devious exploiters at worst. Abundant evidence confirms this observation. Mills has shown that when friends engage in prompt reciprocation, this does not strengthen but rather weakens the relationship (Mills and Clark, 1982). Similarly, favors between friends do not create obligations for reciprocation because friends are expected to help each other for emotional, not instrumental reasons (Mills and Clark, 1994). Other researchers have found that people comply more with a request from a friend than from a stranger, but doing a favor prior to the request increases cooperation more in a stranger than a friend (Boster et al., 1995).Moreover, there is solid empirical evidence indicating that people have a tendency to build long-term cooperative relationships based on largely unconditional cooperation, and are inclined to hold on to them even in situations where this does not appear to be in line with their narrow self-interest (see e.g. Wieselquist et al., 1999). Experiments with exchange situations (Lawler and Yoon, 1996,1993; Kollock, 1994) point to ongoing exchanges with the same partner even if more valuable (or less costly) alternatives are available. This commitment also implies forgiveness and gift-giving without any explicit demand for reciprocation (Lawler, 2001; Lawler and Yoon, 1993). One example is that people help friends and acquaintances in trouble, apparently without calculating present costs and future benefits. Another, extreme example is the battered woman who stays with her husband (Rusbult et al., 1998; Rusbult and Martz, 1995).
This is why de Vos and collaborators (de Vos and Zeggelink, 1997; de Vos et al., 2001; Zeggelink et al., 2000) extended theoretical models with assumptions from evolutionary psychology (Cosmides, 1989; Cosmides and Tooby, 1993). According to evolutionary psychologists, the way our mind functions today is the result of an extremely long evolutionary process during which our ancestors were subject to a relatively stable (social) environment. Individual preferences for various outcomes in typical social dilemmas stabilized in this ancestral environment and still influence the way we decide and behave in similar dilemma situations today.
Our most important addition to these models is that we integrate them into a utility-based framework and provide in this way an efficient method to cover a large range of different strategies. In our model, when an agent has to make a decision, it calculates utilities based on some or all of the information available to it without the ability to objectively assess the consequences of the decision on its overall fitness3. Moreover, we assume that actors are boundedly rational in the sense of being myopic, they evaluate the utility of an action only in terms of consequences in the very near future, i.e. the state of the world that obtains right after they have have taken the action. This exludes the strategic anticipation of future behavior of other agents. Since different agents calculate utility differently, there is variation in behavior. Some of the behaviors lead to better fitness consequences than others. In turn, more successful agents have better chances to stay in the game and to propagate their way of utility calculus to other agents, while unsuccessful ones disappear.
where ![]() expresses materialistic costs of the interaction;
expresses materialistic costs of the interaction;
![]() are agent-specific parameters (or traits) for donation of agent
are agent-specific parameters (or traits) for donation of agent ![]() that determine the weight of the situation-specific parameters in the total utility. In the actual implementation, every time an agent has to make a decision, there is also a probability
that determine the weight of the situation-specific parameters in the total utility. In the actual implementation, every time an agent has to make a decision, there is also a probability ![]() that the agent will make a completely random decision. This random error models noise in communication, misperception of the situation or simply miscalculation of the utility by the agent. Taking this random error into account increases the robustness of our results to noise in general4.
that the agent will make a completely random decision. This random error models noise in communication, misperception of the situation or simply miscalculation of the utility by the agent. Taking this random error into account increases the robustness of our results to noise in general4.
The utility of seeking is defined in the same way, the only difference is that agents may put different weights on the situation-specific decision parameters than in the utility of donation:
Before agents make a decision, be it help seeking or help giving, they calculate the corresponding one of these two utilities for each possible help donor or help seeker. In case of help giving, they choose a partner with the highest utility, if that utility is above an agent-specific threshold ![]() . If the utility of all possible decisions falls below the threshold utility, no help is given to anyone. Otherwise, if there is more than one other agent with highest utility, the agent chooses randomly.
. If the utility of all possible decisions falls below the threshold utility, no help is given to anyone. Otherwise, if there is more than one other agent with highest utility, the agent chooses randomly.
This means that an agent ![]() of the Commitment-type derives more utility from choosing an agent
of the Commitment-type derives more utility from choosing an agent ![]() as an interaction partner, the more times
as an interaction partner, the more times ![]() has helped
has helped ![]() in the past. This is true for choosing from both a group of help seekers and from possible help givers. This also means that the cooperativeness of a Commitment type is unaffected by the fact whether their help was previously refused by an interaction partner.
in the past. This is true for choosing from both a group of help seekers and from possible help givers. This also means that the cooperativeness of a Commitment type is unaffected by the fact whether their help was previously refused by an interaction partner.
If the utility threshold ![]() is positive and
is positive and ![]() the strategy always starts by defecting. Otherwise, it only starts defecting after some initial rounds of cooperation.
the strategy always starts by defecting. Otherwise, it only starts defecting after some initial rounds of cooperation.
A much discussed strategy (type), especially in the experimental economics literature (see e.g. Fehr and Schmidt, 1999; Fehr et al., 2002) is Fairness.7 It is based on the observation that people may be willing to invest in cooperation initially but will require reciprocation of these investments before they are willing to cooperate further. On the other hand people following the fairness principle are also sensitive to becoming indebted, therefore they will be inclined to reciprocate if they are in debt. In other words, their most important aim is to have balanced relationships. Again, translating this strategy class into our framework is straightforward.
Obviously, our approach allows to generate a much larger range of strategies than we discussed above. For our present analysis, it suffices to use these strategy templates but we will explore a larger variety of possible behavioral rules in future work.
We used this result to adjust the most important initial parameters of the model. In other words, we always varied the probability of distress, the cost of help and the cost of not getting help in a way that the above inequality remained true. The actual parameters that we used to draw figures below are:
![]() .
For the entire set of parameter ranges that we tested in the experiments refer to Appendix B.
.
For the entire set of parameter ranges that we tested in the experiments refer to Appendix B.
To assess the relative importance of the ![]() and the
and the ![]() trait, we examined two ``mixed'' versions of Commitment:
trait, we examined two ``mixed'' versions of Commitment:
![]() and
and
![]() . The former version represents a strategy that derives more utility from receiving help than from giving help to a particular partner, whereas the latter version derives more utility from giving than from receiving. Both had high survival statistics. The proportion of replications in which the corresponding Commitment strategy became universal in the simulated group was 64.2% and 72.4%, respectively. The results also hint at a stable positive effect of
. The former version represents a strategy that derives more utility from receiving help than from giving help to a particular partner, whereas the latter version derives more utility from giving than from receiving. Both had high survival statistics. The proportion of replications in which the corresponding Commitment strategy became universal in the simulated group was 64.2% and 72.4%, respectively. The results also hint at a stable positive effect of ![]() on survival success.
on survival success.
The main weakness of AllC compared to Commitment is its lack of an explicit partner selection strategy. Both versions of Commitment are more likely to help those others who have helped them before. Accordingly, a player who tries to exploit Commitment will always be less likely to get help than somebody else who cooperated with AllC, all other conditions being equal. Due to its random partner selection method, AllC is the upper end of not only cooperativeness but of unconditionality as well.
Objective Fairness can be straightforwardly modified in such a way that it becomes more tolerant against temporary fluctuations in the frequency of needing help. For our simulation, we define a corresponding strategy of Tolerant Fairness as
![]() .
.
where ![]() is the probability that another distressed agent also asked and got help from alter, and
is the probability that another distressed agent also asked and got help from alter, and ![]() is the probability that alter is also distressed. Let us assume now that
is the probability that alter is also distressed. Let us assume now that ![]() for all agents. If an agent
for all agents. If an agent ![]() who was not distressed and helped in the previous round becomes distressed now, that agent
who was not distressed and helped in the previous round becomes distressed now, that agent ![]() will face a population of equally preferred others to ask for help. Therefore,
will face a population of equally preferred others to ask for help. Therefore, ![]() will have to choose randomly, facing the same probability
will have to choose randomly, facing the same probability ![]() that the other unlucky ones faced in the previous round. Now, if
that the other unlucky ones faced in the previous round. Now, if ![]() , all agents who gave help before will have a preference for those they helped, and thus
, all agents who gave help before will have a preference for those they helped, and thus ![]() will be reduced in the second round.
will be reduced in the second round.
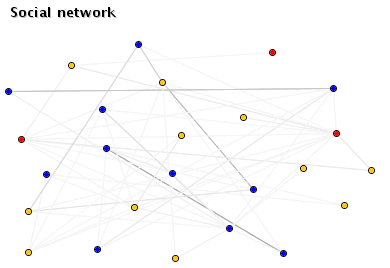
Examining the network structure of all agents (Figure 8) we see again the characteristic strong friendships between Commitment players. Defectors, on the other extreme, clearly attempt to interact with as many others as possible, in search of partners to be exploited. Moreover, we also see some strong ties between Commitment and Fairness agents. What happens in these relationships is that the Commitment player becomes attached to the Fairness player after some initial rounds of helping. The problem for the Commitment agent arises if the relationships becomes unbalanced - Commitment will keep asking its Fairness ``friend'' for help even in the face of repeated refusals. This clearly points to a weakness of Commitment.
|
The general result of Commitment being more successful than Fairness when playing against defectors remained constant throughout this test as well.
A first objection to our study might be that we excluded influences of reputation mechanisms on the relative success of strategies.
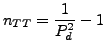
Let
where
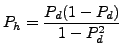
The conditional probability
where
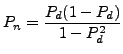
Here ![]() is obtained in the same way than
is obtained in the same way than ![]() above, only
this time the roles of ego and alter are reverted (ego in
need but alter not), which does not affect the result in this case.
above, only
this time the roles of ego and alter are reverted (ego in
need but alter not), which does not affect the result in this case.
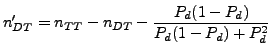
where
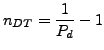
This condition yields after some rearrangement the following result:
/**
* Main cycle of simulation
*/
begin simulation
for each experiment
initialize result variables and charts
for each run
initialize parameters, run-level result variables and charts
initialize society
for each round
initialize round-level result variables
for each agent A
generate a random event R with probability P_d /* probability of distress */
if R occurs distress A
end for
for each subround
for each agent A
if A is distressed call decideWhomToAskForHelp of A
end for
for each agent A
call decideWhomToGiveHelp of A
end for
end for
for each agent A
update fitness
if fitness < f_c remove A from society /* critical fitness threshold */
end for
call replicator_dynamics()
update round-level result variables
update charts if necessary /* if this is a sample round */
if society is empty end run
if there is only one group left in society end run
end for /* end of rounds */
update run-level variables
update charts
end for /* end of runs */
update experiment-level variables
update charts
end for /* end of experiments */
close charts and show results
end simulation
/**
* Agent deciding whether/whom to give help.
*/
begin decideWhomToGiveHelp
if nobody asked for help return nobody
if agent is distressed return nobody
if agent already gave help return nobody
generate a random event R with probability P_err /* decision making error */
if R does not occur
determine group G of agents for whom U_d is maximal /* utility of donation */
if U_d < U_t return nobody /* threshold utility */
else return random agent from G
else
return random agent from {helpseekers+nobody}
end if
end decideWhomToGiveHelp
/**
* Agent deciding whom to ask for help.
*/
begin decideWhomToAskForHelp
remove itself from possible helpers
remove those who refused before in this round
if possible helpers is empty return nobody
generate a random event R with probability P_err /* decision making error */
if R does not occur
determine group G of agents for whom U_s is maximal /* utility of seeking */
return random agent from G
else
return random agent from possible helpers
end if
end decideWhomToAskForHelp
/**
* Evolutionary selection process (based on the replicator dynamics)
*/
begin replicator_dynamics
for each dead agent
calculate society_fitness_sum
for each strategy S in society
calculate strategy_fitness_sum
generate a random event R with probability strategy_fitness_sum / society_fitness_sum
if R occurs create and add agent A with strategy S to new_generation
/* in order to condition successive probability calculations on previous ones */
else decrease society_fitness_sum with strategy_fitness_sum
end for
end for
add new_generation to society
end replicator_dynamics
We wish to thank Henk de Vos, Tom Snijders, Károly Takács and three anonymous reviewers for their inspiring and helpful comments. István Back's research was financially supported by the Ubbo Emmius fund of the University of Groningen.
The research of Andreas Flache was made possible by the Netherlands Organization for Scientific Research (NWO), under the Innovational Research Incentives Scheme.
Axelrod, R. (1984). The Evolution of Cooperation. Basic Books, New York.
Binmore, K. (1998). Review of `R. Axelrod, The complexity of cooperation: Agent-based models of competition and collaboration; Princeton UP 1997'. Journal of Artificial Societies and Social Simulation, 1(1). https://www.jasss.org/1/1/review1.html.
Boster, F., Rodriguez, J., Cruz, M., and Marshall, L. (1995). The relative effectiveness of a direct request message and a pregiving message on friends and strangers. Communication Research, 22(4):475-484.
Cosmides, L. (1989). The logic of social exchange: Has natural section shaped how humans reason? studies with the Watson selection task. Cognition, 31:187-276.
Cosmides, L. and Tooby, J. (1993). Cognitive adaptations for social exchange. In Barkow, J. H., Cosmides, L., and Tooby, J., editors, The Adapted Mind: Evolutionary Psychology and the Generation of Culture, pages 163-228.
de Vos, H., Smaniotto, R., and Elsas, D. A. (2001). Reciprocal altruism under conditions of partner selection. Rationality and Society, 13(2):139-183.
de Vos, H. and Zeggelink, E. P. H. (1997). Reciprocal altruism in human social evolution: the viability of reciprocal altruism with a preference for 'old-helping-partners'. Evolution and Human Behavior, 18:261-278.
Falk, A., Fehr, E., and Fischbacher, U. (2001). Driving forces of informal sanctions. In NIAS Conference Social Networks, Norms and Solidarity.
Fehr, E., Fischbacher, U., and Gächter, S. (2002). Strong reciprocity, human cooperation, and the enforcement of social norms. Human Nature - An Interdisciplinary Biosocial Perspective, 13(1):1-25.
Fehr, E. and Gächter, S. (2002). Altruistic punishment in humans. Nature, 415:137-140.
Fehr, E. and Schmidt, K. (1999). A theory of fairness, competition and cooperation. Quarterly Journal of Economics, CXIV:817-851.
Fishman, M. A. (2003). Indirect reciprocity among imperfect individuals. Journal of Theoretical Biology, 225(3):285-292.
Flache, A. and Hegselmann, R. (1999). Rationality vs. learning in the evolution of solidarity networks: A theoretical comparison. Computational and Mathematical Organization Theory, 5(2):97-127.
Friedman, J. (1971). A non-cooperative equilibrium for supergames. Review of Economic Studies, 38:1-12.
Güth, W. and Kliemt, H. (1998). The indirect evolutionary approach. Rationality and Society, 10(3):377-399.
Hegselmann, R. (1996). Solidarität unter ungleichen. In Hegselmann, R. and Peitgen, H.-O., editors, Modelle sozialer Dynamiken -- Ordnung, Chaos und Komplexität, pages 105-128. Hölder-Pichler-Tempsky, Wien.
Karremans, J., Lange, P. V., Ouwerkerk, J., and Kluwer, E. (2003). When forgiving enhances psychological well-being: the role of interpersonal commitment. Journal of Personality and Social Psychology, 84(5):1011-1026.
Kollock, P. (1993). An eye for an eye leaves everyone blind - cooperation and accounting systems. American Sociological Review, 58(6):768-786.
Kollock, P. (1994). The emergence of exchange structures: An experimental study of uncertainty, commitment, and trust. American Journal of Sociology, 100(2):313-45.
Lawler, E. and Yoon, J. (1993). Power and the emergence of commitment behavior in negotiated exchange. American Sociological Review, 58(4):465-481.
Lawler, E. and Yoon, J. (1996). Commitment in exchange relations: Test of a theory of relational cohesion. American Sociological Review, 61(1):89-108.
Lawler, E. J. (2001). An affect theory of social exchange. American Journal of Sociology, 107(2):321-52.
Mills, J. R. and Clark, M. S. (1982). Communal and exchange relationships. In Wheeler, L., editor, Annual Review of Personality and Social Psychology. Beverly Hills, Calif.: Sage.
Mills, J. R. and Clark, M. S. (1994). Communal and exchange relationships: Controversies and research. In Erber, R. and Gilmour, R., editors, Theoretical Frameworks for Personal Relationships. Hillsdale, N.J.: Lawrence Erlbaum.
Monterosso, J., Ainslie, G., Mullen, P. A. C. P. T., and Gault, B. (2002). The fragility of cooperation: A false feedback study of a sequential iterated prisoner's dilemma. Journal of Economic Psychology, 23(4):437-448.
Nesse, R. M. (2001). Natual selection and the capacity for subjective commitment. In Nesse, R. M., editor, Evolution and the Capacity for Commitment. New York : Russell Sage Foundation.
Nowak, M. A. and Sigmund, K. (1993). A strategy of win-stay, lose-shift that outperforms tit-for-tat in the prisoner's dilemma game. Nature, 364:56-58.
Raub, W. and Weesie, J. (1990). Reputation and efficiency in social interaction: an example of network effects. American Journal of Sociology.
Rusbult, C. and Martz, J. (1995). Remaining in an abusive relationship - an investment model analysis of nonvoluntary dependence. Personality and Social Psychology Bulletin, 21(6):558-571.
Rusbult, C., Martz, J., and Agnew, C. (1998). The investment model scale: Measuring commitment level, satisfaction level, quality of alternatives, and investment size. Personal Relationships, 5(4):357-391.
Schüssler, R. (1989). Exit threats and cooperation under anonimity. The Journal of Conflict Resolution, 33:728-749.
Schüssler, R. and Sandten, U. (2000). Exit, anonymity and the chances of egoistical cooperation. Analyse & Kritik, 22.
Smaniotto, R. C. (2004). `You scratch my back and I scratch yours' versus `love thy neighbour': two proximate mechanisms of reciprocal altruism. PhD thesis, ICS/University of Groningen.
Takahashi, N. (2000). The emergence of generalized exchange. American Journal of Sociology, 105(4):1105-1134.
Taylor, P. D. and Jonker, L. B. (1978). Evolutionary stable strategies and game dynamics. Mathematical Biosciences, 40:145-156.
Vanberg, V. and Congleton, R. (1992). Rationality, morality and exit. American Political Science Review, 86:418-431.
Wieselquist, J., Rusbult, C., Agnew, C., Foster, C., and Agnew, C. (1999). Commitment, pro-relationship behavior, and trust in close relationships. Journal of Personality and Social Psychology, 77(5):942-66.
Wu, J. and Axelrod, R. (1995). How to cope with noise in the iterated prisoner's dilemma. Journal of Conflict Resolution.
Yamagishi, T., Hayashi, N., and Jin, N. (1994). Prisoner's dilemma networks: selection strategy versus action strategy. In Schulz, U., Albers, W., and Mueller, U., editors, Social Dilemmas and Cooperation, pages 311-326. Heidelberg: Springer.
Zeggelink, E., de Vos, H., and Elsas, D. (2000). Reciprocal altruism and group formation: The degree of segmentation of reciprocal altruists who prefer old-helping-partners. Journal of Artificial Societies and Social Simulation, 3(3). https://www.jasss.org/3/3/1.html.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]