J. Gary Polhill, Luis R. Izquierdo and Nicholas M. Gotts (2005)
The Ghost in the Model (and Other Effects of Floating Point Arithmetic)
Journal of Artificial Societies and Social Simulation
vol. 8, no. 1
<https://www.jasss.org/8/1/5.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 09-May-2004 Accepted: 01-Aug-2004 Published: 31-Jan-2005
 Abstract
AbstractBistromathics … is … a revolutionary new way of understanding the behaviour of numbers. … Numbers written on restaurant bill pads within the confines of restaurants do not follow the same mathematical laws as numbers written on any other pieces of paper in any other part of the Universe.
Douglas Adams, Life, the Universe, and Everything (1982)
|
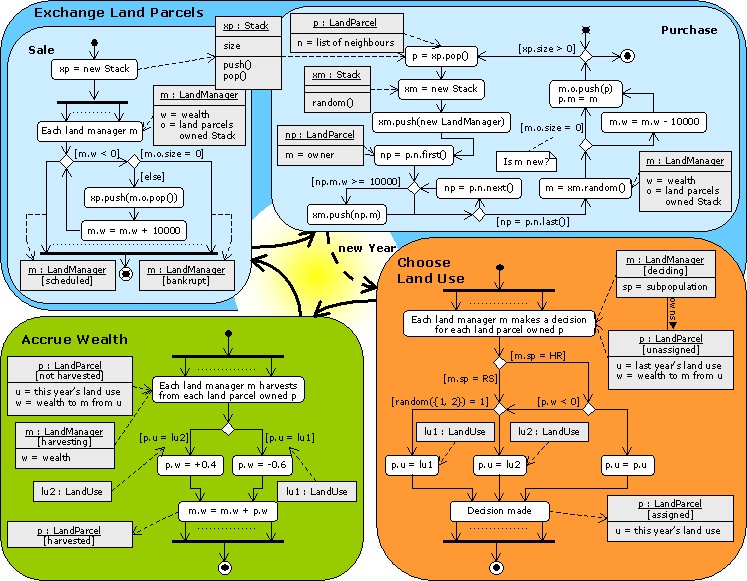
Figure 1. UML-style diagrams based on Booch et al. (1999) showing the yearly cycle. At the simplest level of detail, the coloured boxes represent a statechart diagram showing the flow from one state during the yearly cycle to the other, with the dashed line showing the transition from one Year to the next. Inside each coloured box is an activity diagram showing more detail on the processing involved in each state. Arrows with solid lines represent flow of program control from the start (black circle) to the end (black circle with concentric white ring). Diamonds represent decision points, with one out-flowing arrow labelled with text in square brackets indicating the condition under which that branch is used, and the other out-flowing arrow indicating the 'else' branch. The dotted lines between the arrows to/from the concurrent process (thick) lines indicate many objects engaged in the same activity. Arrows with dashed lines are object flows, indicating the involvement of an object in a particular action. Objects are represented in grey boxes divided into possibly three sections. The topmost shows the object and class, underlined and separated by a colon, with the state optionally in square brackets underneath. The next section, which appears optionally, shows certain instance variables of the object, and the bottom-most section, also optional, shows methods. Comments are indicated in a box with a folded down corner, and connected by a dashed line without an arrowhead to the item with which they are associated. In the 'Purchase' activity diagram, the random() method in the Stack class returns a random member of the stack with equal probability of any member being selected.
|
|
|
| (a) | (b) |
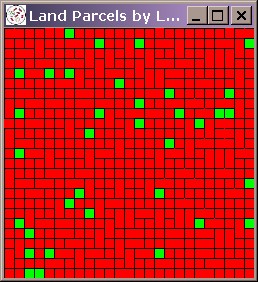
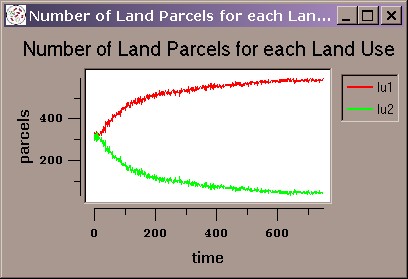
| Figure 2. Systematic bias in a run of the FEARLUS model outlined in Figure 1 using Subpopulation RS only. The space should contain a roughly equal proportion of lu1 (red) and lu2 (green) Land Uses, but by Year 750, the situation is as shown on the left (a). Black lines separate Land Parcels owned by different Land Managers, and the image shows a number of Managers owning two rather than one Land Parcels. The time-series graph in (b) shows the gradual decline in the use of lu2 as more and more ghost Land Managers are created. | |
fcmp package available at http://fcmp.sourceforge.net. Whilst this would probably work in the case above, it is not a generally safe approach in that it does not guarantee any model will behave correctly. This is explored further in Polhill et al. (in press). For this reason we attempted a conversion to interval arithmetic, discussed later.
| dt = D + r(dt - 1 - D) + mt | (1) |
where D is the average dividend (a model parameter), mt is a stochastic component sampled from a Normal distribution with zero mean and constant variance, and r is the autocorrelation parameter: if 0 then dt and dt - 1 are uncorrelated, and if 1, dt and dt - 1 are maximally correlated.
Dividend.m, which declares an external function random() to have a type that conflicts with the declaration in the stdlib.h supplied with Cygwin. This, then, is taken as the baseline version of the ASM.
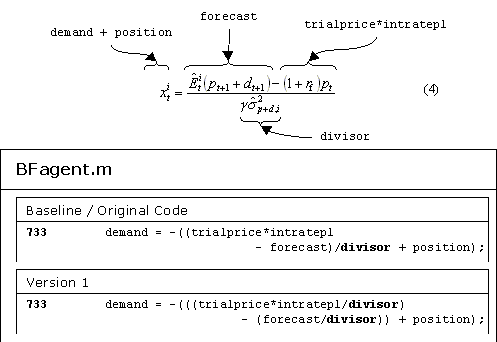
|
Figure 3. Modifications required to create Version 1 of the ASM, involving a change to line 733 of the Objective-C source file BFagent.m. Since division is distributive over subtraction, this change should have no effect according to the laws of arithmetic.
|

|
| Figure 4. Modifications made to the ASM for Version 2 highlighted in bold. (Some irrelevant lines, which are the same in both versions, have been removed.) Essentially, the sum computed in equation (14) in LeBaron et al. (1999) to clear the market for the risky stock is totalled in reverse order of the agents. Since addition is associative, the order the agents are called to make the sum should not make any difference to the behaviour of the model according to the laws of arithmetic. |
asm.scm supplied with the source code. Using a graph plotted at a resolution of 25 time steps, the baseline, Version 1 and Version 2 show a difference in the behaviour of the volume at about the 2000 cycle point, and despite having the same dividend, differences continue to be observed thereafter. To get a precise picture of where the differences occurred, we ran the ASM in batch mode, creating an output data file recording the price, risk free price, and volume each time step to six decimal places. The first difference in output between the baseline and Version 1 occurs at step 1926, whilst that between the baseline and Version 2 occurs at step 2007. Using the recorded output files also enabled us to confirm that the behaviour is initially the same (to six decimal places), and hence that the modifications made in Versions 1 and 2 have not substantially altered the mathematics of the model. The differences in output observed are thus attributable purely to the cumulative effects of the changed floating point rounding errors caused by rearranging the terms in the expressions in alternative but mathematically equivalent ways.
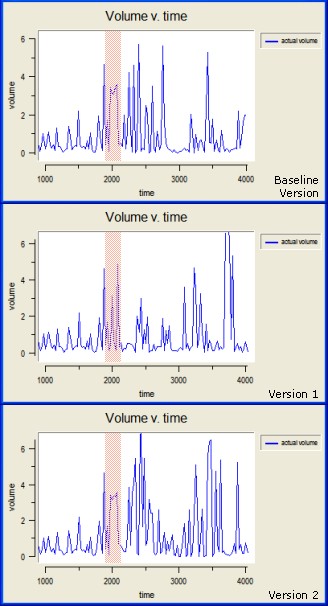
|
| Figure 5. Divergence of behaviour in various versions of the ASM. The same output is seen for the first 2000 cycles or so (though the graphs begin at cycle 1000), but thereafter there are differences in the number, height and width of peaks. The area highlighted in red shows the first differences observed between the versions. Version 1 shows the greater difference from the baseline version in this region, with two thin peaks where the baseline has a single wide peak, whereas Version 2 also features a wide peak but with a flatter top than the baseline. |
| [r1, s1] + [r2, s2] = [f <(r1 + r2), f >(s1 + s2)] | (2) |
| [r1, s1] - [r2, s2] = [f <(r1 - s2), f >(s1 - r2)] | (3) |
|
[r1, s1] × [r2, s2] = [min{f <(r1 × r2), f <(r1 × s2), f <(s1 × r2), f <(s1 × s2)}, max{f >(r1 × r2), f >(r1 × s2), f >(s1 × r2), f >(s1 × s2)}] |
(4) |
|
[r1, s1] / [r2, s2] = [min{f <(r1 / r2), f <(r1 / s2), f <(s1 / r2), f <(s1 / s2)}, max{f >(r1 / r2), f >(r1 / s2), f >(s1 / r2), f >(s1 / s2)}] |
(5) |
| [r1, s1] >L [r2, s2] iff r1 > s2; and [r1, s1] >M [r2, s2] iff s1 > r2 | (6) |
| [r1, s1] <L [r2, s2] iff s1 < r2; and [r1, s1] <M [r2, s2] iff r1 < s2 | (7) |
| [r1, s1] =L [r2, s2] iff (r1 = s2) & (r2 = s1); and [r1, s1] =M [r2, s2] iff (s1 >= r2) & (r1 <= s2) | (8) |
fcmp to floating comparisons without careful consideration of the implications would be unwise.
2In an earlier version of this paper (Polhill et al. 2003) we commented that Epstein & Axtell's (1996) SugarScape features a number of mathematical expressions with potential for floating point issues and yet the source code is not publicly available. The latter may be incorrect. Although Leigh Tesfatsion states on the Agent-Based Computational Economics webpages (http://www.econ.iastate.edu/tesfatsi/acecode.htm) that “the Object Pascal source code for SugarScape is not publicly available”, in a working paper (Axtell, Axelrod, Epstein & Cohen 1995), the authors do state that the code is available from Robert Axtell, and Tobias & Hofmann (2004) classify SugarScape as having an open source licence in the appendix to their paper. In the final draft we therefore decided to give them the benefit of the doubt and have removed the comment here.
3However, this is the precise result of operating on the floating point operands, not on the original numbers the operands may have been rounded from. Thus, for example, the result of 0.4 × 0.1 in IEEE 754 floating point arithmetic is not the nearest representable number to 0.04, but the nearest representable number to the product of the nearest representable number to 0.4 and the nearest representable number to 0.1.
The software used to generate the results in this paper is written in Objective-C for the Swarm libraries. It is released under the GNU General Public Licence, and is available for download at http://www.macaulay.ac.uk/fearlus/floating-point/ghost/.
To reproduce the results in section 2, download FEARLUS model 0-6-2 source code and the associated parameters from the table in the above webpage. This is known to work on a Windows 2000 PC with Swarm 2.1.1, and a Sun Sparc running Solaris 8 with Swarm test version 2001-12-18. Create a directory in which you put the parameter and source code compressed tar files, and decompress them using the following commands from a Cygwin or X terminal:
gunzip -c FEARLUS-model0-6-2.tar.gz | tar xf - gunzip -c FEARLUS-fpdemo.tar.gz | tar xf -
Compile the source code with the following commands, ensuring that your SWARMHOME environment variable points to the appropriate location:
cd model0-6-2 make
To run the FEARLUS model as described in Figure 1, issue the following commands:
cd ../demo/fp ../../model0-6-2/model0-6-2 -S 1552078961 -p RH-fp.model -o demo.obs
Not all seeds generate ghost land managers. To try other seeds, replace the -S 1552078961 in the command above with -s. If you are using Swarm 2.1.1, note that -S should be replaced with -X.
To get a result similar to that shown in Figure 2, do:
../../model0-6-2/model0-6-2 -s -p R-fp.model -o demo.obs
The interval arithmetic version of FEARLUS (0-7) is also available from the above website. The default version to download is FEARLUS-model0-7.tar.gz, but on PCs, the Cygwin environment supplied with Swarm 2.1.1 does not implement the C API hardware rounding function fpsetround(). For PCs with a Pentium CPU, you can download FEARLUS-model0-7ci.tar.gz which contains some extra code to implement this function.
The code used to estimate the likelihood of condition (b) in Section 2 is supplied in lu1lu2sequences.c. It can be compiled and run thus:
gcc -o lu1lu2sequences lu1lu2sequences.c ./lu1lu2sequences
The results given here apply to running this program on a Sun Sparc platform running Solaris 2.8 and quoting the line of output beginning 'i = 5' (the program loops rather optimistically until i = 40, so will need to be interrupted after this line has been displayed). If you run the program on an Intel PC, it is likely you will get different results for the reasons discussed in Section 4. For example, on one Pentium 4 PC we got 7496 having Wealth exactly equal to zero and 7195 with floating point errors resulting in a positive Wealth (as per the Sun), but only 27144 (about 19%) with a negative Wealth small enough that when subtracted from 10000 the result is 10000, as opposed to the 97536 on the Sun. Here then, Intel's 80-bit arithmetic has worked out favourably.
The ASM version 2.4 requires a later version of Swarm. We used Swarm 2.2 pretest 10 on a Windows XP PC to generate the results in Figure 5. To generate the results shown here, either download the collection of premodified versions of the source code from the website given at the beginning of this section, or download the original ASM-2.4 from http://artstkmkt.sourceforge.net and follow the instructions in Section 3 for modifying the code. Once you have the three versions of the software (baseline, Version 1 and Version 2) in separate directories, compile them with:
make EXTRACPPFLAGS=-DNO_HDF5and run each one from its own directory with the command:
./asm -S 123654789
In the ObserverSwarm pop-up window, you can change the time interval by setting the 'displayFrequency' parameter. The graphs in Figure 5 were generated using an interval of 25.
To generate output data files with 1 step time intervals, modify the parameter file asm.scm in each version's directory so that the BatchSwarm section reads:
(cons 'asmBatchSwarm
(make-instance 'ASMBatchSwarm
#:loggingFrequency 1
#:experimentDuration 10000
))
Then run each version model using:
./asm -b -S 123654789
The output will appear in a file beginning with the name output.data. This can be compared with the output from other versions using the diff command.
ABRAMS, S L, CHO, W, HU, C-Y, MAEKAWA, T, PATRIKALAKIS, N M, SHERBROOKE, E C, & YE, X (1998) Efficient and reliable methods for rounded-interval arithmetic. Computer-Aided Design 30 (8) pp. 657-665.
ALEFELD, G, & HERZBERGER, J (1983) Introduction to Interval Computation. New York: Academic Press.
BADEGRUBER, T (2003) Agent-Based Computational Economics: New Aspects in Learning Speed and Convergence in the Santa Fe Artificial Stock Market. Inaugural dissertation, Universitat Graz, Graz, Austria.
BOOCH, G, RUMBAUGH, J, & JACOBSON, I (1999) The Unified Modeling Language User Guide. Boston, MA: Addison-Wesley.
CHEN, S-H, & YEN, C-H (2002) On the emergent properties of artificial stock markets: the efficient market hypothesis and the rational expectations hypothesis. Journal of Economic Behavior & Organization 49 pp. 217-239.
COLLIER, N (1996-) RePast: An extensible framework for agent simulation. http://repast.sourceforge.net/.
DEKKER, T J (1971) A floating point technique for extending the available precision. Numerische Mathematik 18 pp. 224-242.
EDMONDS, B, & HALES, D (2003) Replication, replication and replication: Some hard lessons from model alignment. Model to Model International Workshop, GREQAM, Vielle Charité, 2 rue de la Charité, Marseille, France. 31 March - 1 April 2003. pp. 133-150.
EPSTEIN, J M, & AXTELL, R (1996) Growing Artificial Societies: Social Sciences from the Bottom Up. Cambridge, MA: MIT Press.
GAO. 1992. Patriot Missile defense: Software problem led to system failure at Dhahran, Saudi Arabia. GAO/IMTEC-92-26, Washington, DC: U.S. Government Accountability Office. Available on-line at http://161.203.16.4/t2pbat6/145960.pdf.
GOLDBERG, D (1991) What every computer scientist should know about floating point arithmetic. ACM Computing Surveys 23 (1) pp. 5-48. Reproduced in Sun's Numerical Computing Guide (Appendix D) and available on-line at http://portal.acm.org/citation.cfm?doid=103162.103163
GOTTS, N M, POLHILL, J G, LAW, A N R (2003) Aspiration levels in a land use simulation. Cybernetics & Systems 34 (8) pp. 663-683
HIGHAM, N J (2002) Accuracy and Stability of Numerical Algorithms, 2nd Edition. Philadelphia, USA: SIAM.
IEEE (1985) IEEE Standard for Binary Floating-Point Arithmetic, IEEE 754-1985, New York, NY: Institute of Electrical and Electronics Engineers.
INTEL (2003) IA-32 Intel Architecture Software Developer's Manual Volume 1: Developer's Manual. http://www.intel.com/design/Pentium4/manuals/.
JOHNSON, P E (2002) Agent-Based Modeling: What I learned from the Artificial Stock Market. Social Science Computer Review 20 pp. 174-186.
KAHAN, W, & DARCY, J D (2001) How Java's floating point hurts everyone. Originally presented at the ACM 1998 Workshop on Java for High-Performance Network Computing, Stanford University. Revised and updated version (5 Nov 2001, 08:26 version used here) available online at http://www.cs.berkeley.edu/~wkahan/JAVAhurt.pdf.
KNUTH, D E (1998) The Art of Computer Programming Vol. 2. Seminumerical Algorithms. Third Edition. Boston, MA: Addison-Wesley.
KRIPKE, S (1963) Semantical considerations on modal logic. Acta Philosophica Fennica 16, pp. 83-94.
LAWSON, C L, & HANSON, R J (1995) Solving Least Squares Problems. Philadelphia, PA: SIAM.
LEBARON, B, ARTHUR, W B, & PALMER, R (1999) Time series properties of an artificial stock market. Journal of Economic Dynamics & Control 23 pp. 1487-1516.
LIONS, J-L (1996) Ariane 5 Flight 501 Failure: Report by the Inquiry Board. Paris: European Space Agency. Available online at http://ravel.esrin.esa.it/docs/esa-x-1819eng.pdf.
MCCULLOUGH, B D, & VINOD (1999) The numerical reliability of econometric software. Journal of Economic Literature 37 (2) pp. 633-665.
MINAR, N, BURKHART, R, LANGTON, C, ASKENAZI, M (1996-) The Swarm simulation system: A toolkit for building multi-agent systems. http://wiki.swarm.org/
MOSS, S, GAYLARD, H, WALLIS, S, & EDMONDS, B (1998) SDML: A multi-agent language for organizational modelling. Computational & Mathematical Organization Theory 4(1) pp. 43-69.
PARKER, M (1998-) Ascape. http://www.brook.edu/dybdocroot/es/dynamics/models/ascape/. The Brookings Institution.
POLHILL, J G, GOTTS, N M, & LAW, A N R (2001) Imitative and nonimitative strategies in a land use simulation. Cybernetics & Systems 32 (1-2) pp. 285-307.
POLHILL, J G, IZQUIERDO, L R, GOTTS, N. M. (2003) The ghost in the model (and other effects of floating point arithmetic). Proceedings of the first conference of the European Social Simulation Association, held in Groningen, Netherlands, 18-21 September 2003, published online at http://www.uni-koblenz.de/~kgt/ESSA/ESSA1/.
POLHILL, J G, IZQUIERDO, L R, GOTTS, N. M. (in press) What every agent based modeller should know about floating point arithmetic. Environmental Modelling and Software.
SHLEIFER, A (2000) Inefficient Markets: An Introduction to Behavioral Finance. Oxford UP.
SKEEL, R. (1992) Roundoff error cripplies Patriot missile. SIAM News 25 (4) p. 11. Available online at http://www.siam.org/siamnews/general/patriot.htm.
SUN MICROSYSTEMS (2001) Numerical Computing Guide. http://docs.sun.com/source/806-3568/.
TOBIAS, R & HOFMANN, C (2004) Evaluation of free Java-libraries for social-scientific agent based simulation. Journal of Artificial Societies and Social Simulation 7 (1). https://www.jasss.org/7/1/6.html
ULLRICH, C, & VON GUDENBERG, J W (1990) Different approaches to interval arithmetic. In Wallis, P. J. L. (Ed.) Improving Floating Point Programming, ch. 5. Chichester, UK: John Wiley & Sons.
WALLIS, P J L (1990a) Basic concepts. In Wallis, P J L (Ed.) Improving Floating Point Programming, ch. 1. Chichester, UK: John Wiley & Sons.
WALLIS, P J L (1990b) Machine arithmetic. In Wallis, P J L (Ed.) Improving Floating Point Programming, ch. 2. Chichester, UK: John Wiley & Sons.
WINKLER, J R (2003) A statistical analysis of the numerical condition of multiple roots of polynomials. Computers & Mathematics with Applications 45 (1-3) pp. 9-24.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]