Scott Moss (2001)

Game Theory: Limitations and an Alternative

Journal of Artificial Societies and Social Simulation vol. 4, no. 2,
<https://www.jasss.org/4/2/2.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary

Received: 01-Nov-00      Accepted: 01-Feb-01      Published: 31-Mar-01

Abstract

The purpose of this paper is to describe current practice in the game theory literature, to identify particular characteristics that ensure the literature is remote from anything we observe and to demonstrate an alternative drawn from agent based social simulation. The key issue is the process of social interaction among agents. A survey of game theoretic models found no models representing interaction among more than three agents, though sometimes more agents were involved in a round robin tournament. An ABSS model is reported in which there is a dense pattern of interaction among agents and outputs from the model are shown to have the same statistical signature as high-frequency data from competitive retail and financial markets. Moreover, the density of agent interaction is seen to be necessary both to obtain the validating statistical signature and for simulated market efficiency. As far as competitive markets are concerned, game theoretic models evidently assume away the source of the properties observed in real high frequency data and also the properties required for market efficiency.

Keywords:

game theory, agent, multi agent system, simulation, market, intermediation

Introduction

1.1

The purpose of this paper is to describe current practice in the game theory literature, to identify particular characteristics that ensure the literature is remote from anything we observe and to demonstrate an alternative drawn from agent based social simulation.

1.2

Current practice in game theory is described in section 5 on the basis of all papers with the word "game" or "games" in their titles or abstracts or among their keywords and published in the Journal of Economic Theory (JET) in 1999. There were 14 such articles out of 87 published in that year. Their bibliographic details are listed in the Appendix. JET was chosen as the source for these articles because it is a grade A journal publishing articles by practitioners working at the leading edge of economics.

1.3

In general terms, we find that, of the 14 articles considered, six do not represent any process whatsoever, seven posit processes entailing interaction among two agents at a time, one posits a processes entailing interaction among three agents. In all of the papers, agents are motivated by continuous, convex utility functions. They have varying degrees of knowledge about the future (in the extreme, perfect and unlimited foresight) and about other agents in the present (in the extreme, all possible collaborative acts of all possible coalitions of agents).

1.4

The alternative approach considered here - an application of agent based social simulation - is one which represents social process involving limited knowledge of other agents but substantial interaction among agents that do know one another. In addition, agents have preferences but these are not represented as continuous convex functions. Agents can be induced to change their behaviour but this requires some non-negligible social pressure or some other evidence that their previous behaviour is no longer functional or, at least, is less functional than other behaviours the agent can devise.

1.5

Clearly both approaches involve specifications that are simple relative to real social systems. The issue is whether the simplifications support representations of real, target social systems or, alternatively, whether they impose crucial misspecifications. The test is whether the models incorporating such simplifications can be validated with respect to the target systems. In order to demonstrate that agent based social simulation provides the basis for constructing models as reflections of observed target social systems, a model is reported with results that have the statistical signature of a target social system. The particular target system is a class of markets. It cannot therefore be claimed that the ABSS model reported below is concerned with phenomena that are in principle different from the phenomena of concern to economic game theorists. That game theory as represented by the articles published in the 1999 Journal of Economic Theory cannot in principle capture the same statistical signature is demonstrated by an analysis of the common characteristics of those models.

A Statistical Signature of Competitive, Intermediated Markets

2.1

Consumers typically do not purchase the goods they consume directly from the producers. Virtually all consumed goods are purchased from retailers or, occasionally, wholesalers. In general, the retailers and wholesalers are, in the language of the old fashioned financial markets, jobbers who buy goods in order to sell them on. There are traders who do not take the ownership or even the possession of the commodities they sell. Indeed, it is obviously not possible for a jobber to purchase a service to sell on. All services must be purchased directly from the producer - for example a plumber's services, transportation or travel - or they must be arranged by an intermediary. Intermediaries who arrange transactions but do not take ownership of the commodity being bought and sold is, again in the language of the financial markets, a broker.

2.2

In this paper we consider jobbers in goods sold for consumption in households. The four plots in Figure 1 indicate that market shares in competitive retail trades have a power law distribution N(s) ~ s-a where s is some measure of size and N is some measure of the number of observations at that size. This relationship obviously implies a straight line on double log scales. The data from which those plots have been drawn are reproduced in Table 1. Evidently, the most competitive markets are those with the steepest slope of the trend line of cumulative market share plotted against percentages of outlets.

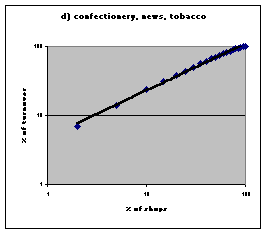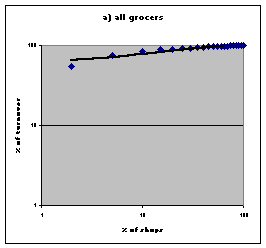
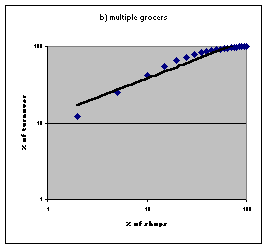
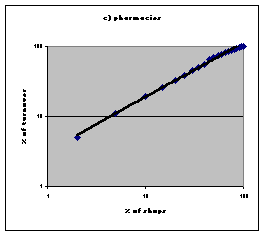
Figure 1. Power law distributions in retail trades in the United Kingdom. Source: Nielsen 1992.

2.3

An important property of any power law distribution is that the distribution function has a fat tail. That is, the frequencies of any value in the population do not converge to zero as the value is further from the mean. Another way of stating this property is that the variance of the distribution is not finite.

2.4

We see from Figure 1 and Table 1 that the relationship between the number of shops and their cumulative market share is closer to the trend line as the industry is more competitive as measured by the market shares of the largest x per cent of outlets. This empirical result coheres well with the circumstances in which, by observation and simulation, we know power law distributions to emerge. These circumstances are where there is considerable interaction among the components of a system and those components are meta- stable. (Jensen, 1998). An entity is meta stable if it does not change its characteristics or behaviour until some threshold force has been applied to it. Consequently, power law distributions mark avalanches, earthquakes, traffic systems, income distributions, and a whole host of other natural and social phenomena. (Bak, 1997). That social phenomena are clear and important sources of power law distributions is evidenced by the fact that the first identification of power law distribution was by Vilfredo Pareto (Pareto, 1896) who found that the personal distribution income is a power law distribution. 

Table 1: Cumulative market share of largest x% of shops
% of shops	all grocers	mult. Grocers	pharmacies	cnt
2	54	12	5	7
5	75	25	11	14
10	85	42	19	24
15	89	55	26	31
20	90	65	33	38
25	92	72	39	44
30	93	78	45	50
35	94	83	50	56
40	95	86	56	61
45	96	88	65	66
50	97	91	69	70
55	97	92	74	74
60	98	94	78	78
65	98	95	81	82
70	98	96	85	85
75	99	97	88	89
80	99	98	92	92
85	99	99	95	95
90	100	99	98	97
95	100	100	100	99
100	100	100	100	100

2.5

If a power law distribution emerges from interaction among metastable entities, then the process generating the data is incompatible with any equilibrium of the system. Bak (Bak, 1997), drawing on Nagel and Paczuski (1995), nicely identifies the difference between critical systems and equilibrium systems. Nagel and Paczuski simulated traffic movements in a one- dimensional cellular automata model. Cars could move an integer number of cells from 0 to 5 in each time step. They could reduce this "speed" more quickly than they could accelerate. At low traffic densities, every car could travel at a speed of 5 cells per time step. In principle, every car could travel at 5 cells per time step. This is simple to programme. But, when there is a high density of traffic, if any one car should reduce its speed to 4 cells per time step, then the "knock-on" effects of that speed reduction immediately create a traffic jam and the size of that traffic jam as measured by the number of cars travelling at a speed constrained below 5 by the speed of the car ahead changes over time. The distribution of traffic jam sizes is a power law distribution and the original state in which all cars travelled at 5 cells per time step is never again achieved.

2.6

The argument of this paper is that economic equilibrium is a class of states of which a particular instance is canonically equivalent to all of the cars in the Nagel-Paczuski model travelling at their maximum speed. However, markets made by intermediaries will exist only in critical states canonically equivalent to the Nagel-Paczuski model with traffic jams. With a sufficient density of traders and allowing for entry to the market by intermediaries, an intermediated market will be in a critical state. That state will be self-organised in the sense that it is not necessary to tune the parameters of the system to achieve the occasional bouts of disorder where the scales and frequencies of the disorder are power law distributed. This makes it different from so-called chaotic systems that can be achieved only by tuning parameters.

2.7

Economic theory contains many proofs of sufficient conditions for a system to be in equilibrium and for that equilibrium to be efficient in the sense that no agent can be better off without at least one other agent being worse off - Pareto efficiency. It also implies that, given prevailing prices and incomes, both production output and household satisfaction are maximised. This is closely analogous to the maximum throughput of cars in the Nagel-Paczuski model requiring all cars to be travelling at the maximal 5 cells per time step. Of course that equilibrium is highly unstable and in the face of any minor disturbance self-organises into a critical state. Bak (1997, p. 198) argues that "the critical state is the most efficient state that can actually be reached dynamically. A carefully engineered state where all the cars were moving at velocity 5 would have higher throughput, but it would be catastrophically unstable. This very efficient state would collapse long before all the cars became organised."

2.8

The model reported in section 3 demonstrates conditions in which market dynamics result in self-organised criticality of the system and that criticality is necessary for the satisfaction of the bulk of consumers' demands.

A Model of Intermediated Markets Validated by Statistical Signature

Model specification

3.1

The simulation model reported here was devised to assess conditions in which agent trading could take place in large systems and to demonstrate the constructive use of statistical signatures. The key elements of this model are:

1. The system is sufficiently large that each agent can see only a small part of it.
2. Agents can communicate directly with other agents that are known to them in order to exchange information about the existence of other agents.

3.2

These conditions suggest an analogy with "word of mouth" communication in social systems. Each agent can "see" or know a small subset of all agents. Just as people know other people who are geographically close or functionally similar to themselves, agents will see other agents in close proximity represented by direct links in a network of agents. Moreover, they will be able to find out about the existence of agents to which there is at least one path defined by agents that know other agents.

3.3

A standard representation of such a network is agents placed on a grid. If it is relevant that some agents are at the periphery of the network, then the appropriate grid is projected onto a finite plane surface. Those agents towards the edges of the plane will have direct links to fewer agents than will agents towards the centre of the plane. If such "edge effects" are not of interest, then the appropriate grid is projected onto a torus. As a first step in developing statistical signatures for systems and using those statistical signatures to identify appropriate or inappropriate agent specifications for such systems, it seems appropriate to implement the conceptually simplest possible model that has the desired system properties. For this reason, to avoid the complication of edge effects, the agent network is represented by a toroidal grid populated by agents that can "see" a limited number of cells in each of the four cardinal directions.

Model structure

3.4

Cognitive agents in the model buy and/or sell items. These items are represented by the values of digits in an ordered list - a digit string. This could be a bit string (if the allowable digits are 0 and 1) but, in general, the values of the digits in the string can be to any arbitrary base. At each trading cycle, an abstract agent produces a digit string. The values of the digits could represent information or the characteristics such as colour or weight of goods. The length of the string is constant over each simulation run and is determined at the start of each run by the model operator.

3.5

The model operator also determines a number of item sources distributed at random on the grid. Each source holds the current values of digits at specified positions in the digit string. These values change as the system digit string changes.

3.6

Jobbers are cognitive agents that acquire the values of digits from sources. These values can be acquired only as packets of all items held by a source. However, the jobbers can sell items individually or in any combinations available to them. That is, they can "break bulk" by selling on to other agents only those items from a source that the other agents demand and they can combine the items acquired from several sources. The number of jobber agents entering the market at each time step (the trading cycle) is chosen at random from the [1, J] interval where J is set by the model operator. Each jobber begins life with no assets and builds asset reserves from profits on the purchase and sale of items acquired either from sources or from other jobbers. A jobber leaves the market when its asset reserves are exhausted. One consequence of this specification is that a jobber's sales revenue must exceed the cost of its acquisitions in the first trading cycle of its life.

3.7

Each jobber agent is initially allocated to an empty cell but can choose to move to some other cell if it is unoccupied and no other agent is seeking to move at the same time to the same cell. The motivation to change cells is the knowledge that there is a profitable jobber in the neighbourhood of the destination cell.

3.8

Customers are cognitive agents that either acquire packets of digit values from sources in the same way as do the jobbers or they buy demanded items from the jobbers or some combination of these. The customer agents each inhabit a given cell during the whole of the simulation run. Although the number of customer agents is determined at the start of each run by the model operator, their locations are determined at random.

3.9

At the start of each simulation run, customer agents are allocated demands for the values of digits at specified positions in the system digit string. The number of items demanded is determined at random from the [1, C] interval where C is set by the model operator at the start of the simulation run. Brokers have no demands of their own but only demands for items for which they have previously received enquiries from customers or other brokers.

3.10

Jobbers and customers are synchronous, parallel agents. To enable them to communicate with one another, a series of communication cycles is nested within each trading cycle. A limit of eight communication cycles was allowed within each trading cycle though there would have been fewer communication cycles if all demands were filled earlier. In practice, this never happened in the experiments reported here.

Agent cognition

3.11

There are two principle aspects to the representation of agent cognition: the problem space architecture taken from Soar (Laird et al., 1986) and ACT-R (Anderson, 1993) and the endorsements mechanism as adapted from Cohen (Cohen, 1985). The problem space architecture is described in Figure 2.

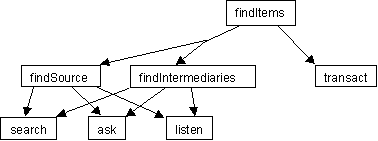Figure 2. The cognitive agents' problem space architecture.

3.12

The goal was to find items in demand. The initial subgoals were to find sources and find intermediaries with the further subgoals to search over the visible cells, to ask suitable agents known to the agent and to listen for their requests or replies to the agent's own requests. Once answers had been heard, if those answers provided suitable information about available items from either sources or intermediaries, then the agent would adopt the transaction subgoal.

3.13

The urgency of acquiring any particular item - the value of the digit at any particular position in the system digit string - was determined by endorsements. Items that changed frequently in value were valued more highly than items that changed infrequently. The frequency of change was learned by experience and was in fact determined by a mutation probability. The maximum mutation probability and the (tanh) distribution of probabilities among positions of the digit were set for the duration of the simulation run by the model operator.

3.14

The choice of broker, when there was a choice, was also determined by endorsements. Brokers that were known to the agent and had been reliable in the past or relatively inexpensive and that provided most or all of the items demanded by the purchasing agent were preferred to agents that lacked any of those endorsements. A fuller description of the endorsements mechanism as used in the model reported here is to be found in several papers (e.g., Moss et al., 1996; Moss, 1998, Moss, 2000a, Moss, 2000b).

Communication among agents

3.15

In order to concentrate on the effects of word of mouth communication, agents were not programmed to broadcast information. Direct communication among agents in SDML takes the form of the sending agent placing the desired clause on the database of the receiving agent. Because agents are parallel, synchronous agents, it is not feasible for one agent to change the state of another agent while that other agent is changing its own state. Consequently, SDML allows parallel agents to access clauses placed on their databases by other agents only at the following common time step - in the case of the present model, at the subsequent communication cycle.

3.16

Being able to follow links from one agent to another to get or give information is effectively word-of-mouth communication. One agent can communicate with another agent within its horizon. If the second agent informs the first agent of the existence and address of a third agent beyond the first agent's horizon, then the first agent will be able to communicate directly with that third agent. If the third agent informs the first agent of the address of a fourth agent, then communication from the first to the fourth agent becomes possible. This procedure was implemented for consumer agents to engage in word of mouth communication concerning the locations of both brokers and sources. Broker agents lacked the functionality to pass on that information since it would be commercially valuable to them.

Parameter values

3.17

All of the simulation runs employed parameter settings that were taken exactly from runs of Moss' (Moss, 2000a) unit-square model. The system digit string contained 40 digits; there were 15 sources and 100 customers. Each customer could demand up to 12 items and each source could hold up to 15 items.

3.18

The permitted number of entrants as brokers in the market was shown in the unit-square model to have no effect on the efficiency of intermediated exchange. The maximum number of broker agents that could enter the market in any trading cycle was therefore set at 15 which is rather higher than in the runs with the unit-square model. The choice of a larger number of entrants was motivated by the intention to investigate the effect of word of mouth communication among agents: with more brokers in the market there was more information for customer agents to communicate by word of mouth.

3.19

In all runs, agents could identify the existence of sources or other agents within eight cells of their own position in the cardinal directions (up, down, right and left).

3.20

The only parameter setting that was changed for the different simulation runs was the size of the grid. Three grid sizes were used: 50x50 (2500 cells), 30x30 (900 cells) and 25x25 (625 cells).A larger grid size implies a lower density of agents.

Simulation results

4.1

Experimentation confirmed that agent density is a critical factor in the viability of agent trading, more surprisingly that a high proportion of demands are satisfied only when virtually all trading is via intermediary agents and that the power law distribution characterises market shares among trading agents when intermediation is viable. The results presented in this section bring out the relationship between agent density and, in turn, market effectiveness, pricing, the extent of intermediation and the nature and role of the statistical signature.

Market effectiveness

4.2

One natural measure of the effectiveness of markets is the proportion of total customer demands that are satisfied through transactions. The time series of these proportions for three scales of grids are shown in Figure 3. The population density of customers and sources increases from figure 3a down to 3c. With a density of one customer in every 25 cells, as in the run reported in Figure 2a, on average 3.2 per cent of demands were filled. With one customer for every nine cells, the percentage of filled demands rose to 14.6 per cent but the supplies were very erratic. The reason for the erratic nature of the supplies was that jobbers typically found sources for items that potential customers wanted but the number of such items was sufficiently small that the revenue typically did not cover the transportation and storage costs. The survival of brokers in the environment modelled here, as in the unit-square environment (Moss, 2000a), requires each broker to be able to sell on to several customers the same items obtained from a small number of sources. In that way, the transportation charges to a point close to the customer agents as well as the storage or processing charges are incurred once for a relatively large number of sales. This enables the broker to undercut the cost to the customer of acquiring the items directly from sources because the broker is able to share out the same costs among several customers.

Prices

4.3

When agents are distributed so densely that every agent knows every other agent and also knows every source, then the customer agents can compare the cost of items from intermediaries with the cost of acquiring them directly from sources. Provided that customer agents always choose the cheaper source, broker agents will have to keep their prices sufficiently low that the total costs of exchange in the system are less than they would be in the absence of intermediation.

4.4

Once the density is attenuated in any way, the choice for customers is no longer whether they engage in direct exchange with the sources or intermediated exchange with brokers. The choice becomes one of trading or not since, at less than the highest densities, not all sources will be known to all customer agents. In this case, unless some expenditure constraint is imposed on the customer agents, there is nothing to limit price. Increasing rates of price inflation were indeed encountered in the 625-cell simulation but these obviously had no effect on the volume or stability of trade.

4.5

No attempt was made in these models to introduce price competition among brokers although the customer agents did positively endorse brokers they knew to be cheaper than others and, so, other things being equal, would choose the brokers offering lower prices. At the same time, they valued reliability - orders translating into deliveries - more highly the cheapness.

4.6

We conclude that, while price competition and low prices generally are doubtless important features of some systems (for example, real societies), price competition is not a core consideration for the functioning of exchange processes in large systems.

(a) 50x50 grid (2500 cells)

(b) 30x30 grid (900 cells)

(c) 25x25 grid (625 cells)

Figure 3 . Agent densities and sales volumes in relation to demands

The extent of intermediation

4.7

Demand satisfaction in all of the modelled markets was very largely a result of intermediated transactions. In Figure 3, the time series in each case represents, from the bottom up, acquisitions of items by customers directly from sources and the total of satisfied demands. The horizontal topmost line is total demand. Evidently, in all cases direct acquisition from sources was negligible.

4.8

In the most successful (most densely populated) market, intermediary agents were not on average very long lived and, as indicated in Figure 4, there were always a large number of broker agents.

4.9

Because there was a stream of broker agents entering the market, each of them would attract demand enquires from and make supply offers first to agents within their visibility horizon and would communicate with increasingly distant customer agents as knowledge of their existence spread by word of mouth. Consequently, their customers would tend to be relatively close to them. This gives scope for a larger number of brokers to be active in a large system than in a small system ( i.e. a system where every agent knows every other). As is seen from Figure 4, once the market became established, the effective system was marked by a gaggle of brokers.

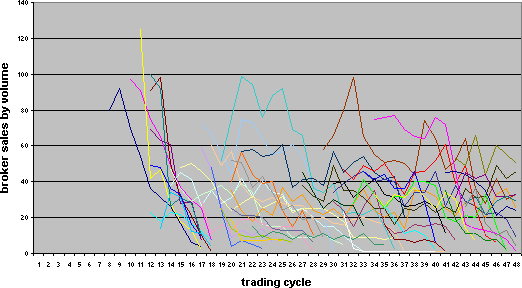
Figure 4. Intermediaries' sales volumes in a 25x25 (625 cell) grid

Statistical signatures

4.10

The logarithms of the market shares of the intermediaries in the market the 20 ^th, the 30 ^th , the 40 ^th and the 50 ^th cycles of a simulation run were plotted against the logarithms of their size rank. A linear relation indicates that market shares are power law distributed. The evidence is presented in Figure 5 and in Table 2.

4.11

The vertical axis in Figure 5 is market shares and the horizontal axis is the rank of the jobbers by market share. The R² of the linear regression on the data in that figure is in excess of 0.98. The data is clearly power law distributed.

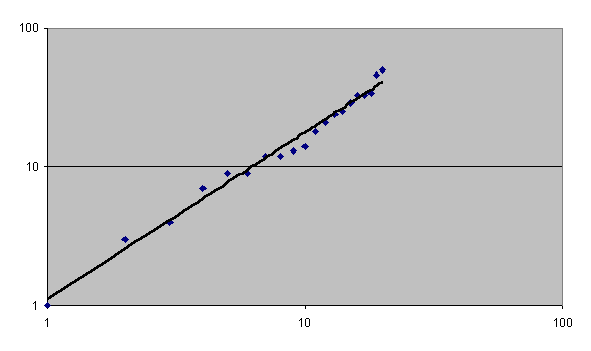
Figure 5. Intermediaries' sales obey the power law at trading cycle 49

Table 2: Regression estimates of power law log y = log a + b log x
trading cycle	a	b	R- square
19	- 0.73751	1.555198	0.953736
29	- 0.44535	1.477288	0.988578
39	- 0.90515	2.042664	0.942295
49	0.04263	1.204543	0.983854

4.12

As indicated in Table 2, the parameters of the distribution were significantly different at each of the time steps for which that data is represented. The differences are statistically significant at any confidence level up to at least 11 significant digits. Moreover, there is no obvious trend. As with the empirical market share data reported in Table 1 the steeper slopes of the power function correspond to less skewness in the market share distribution or, in conventional economic terminology, greater competitiveness. None of the simulation experiments led to convergence in the degree of competitiveness of the market.

4.13

A crucial question in the assessment of the value of this sort of simulation model in comparison with the value of game theoretic or other economic models is the importance of the dynamics of the process captured by the model. The representation of cognition results in metastability of the consuming agents' choices of the intermediaries from which they obtain demanded items. The jobbers are valued for their reliability in meeting orders, for the range of items they offer that the consumer demands, and similar characteristics. If a jobber becomes less reliable or changes the composition of the items it supplies so that the consumer has to make more purchases of smaller lots and therefore incur higher costs of exchange, then the consumer will be more likely to try other jobbers and to find other jobbers that the consumer values more highly. However, there is some inertia here and the consumer is no more likely to change trading partners because of a single instance of unreliability or a single relevant change in the range stocked than real consumers are likely to change their consumption patterns as a result, say, of a half-penny rise in the price of a tin of tuna.

4.14

Moreover, the market functioned more efficiently as the density of the consumers and sources in the market was greater. There was, as a result, more interaction in the form of more intense word of mouth communication among the consumer agents.

4.15

In short, there was a level of interaction among the metastable agents which generated the power law distribution of market shares and the satisfaction of more than 90 per cent of total demands. Without the intensity of interaction, jobbers could not survive in the market and few demands were satisfied. This result coheres with Bak's analysis of the traffic jam simulation and with the conditions for self organised criticality. The question remaining, and to which we now turn, is whether a similar statistical signature could be generated from a game theoretic model.

Can Game Theoretic Models Have the Statistical Signature of Intermediated Markets?

5.1

Real intermediated markets, if they are competitive, are characterised by power law distributed market shares. The more competitive is the market, then the larger is the magnitude of the exponent in the power law equation. Interaction among dense networks of meta-stable agents are known from simulation experiments in many scientific fields to generate such power law distributions. An analysis of the current state of the art in game theory as represented by the 14 game theoretic papers in the 1999 Journal of Economic Theory indicates that game theoretic models cannot capture the necessary interaction as a dynamic process.

Small-number games

5.2

Seven of the 14 papers reported models of two-person games and one reported a three-person game. Two- and three-person networks cannot be remotely sufficient to support self organised criticality.

5.3

The two-person games were reported by Stamland ( 1999), Battigalli and Siniscalchi (1999), Wallner ( 1999), Alós- Ferrer (1999 ) and Sáez-Martí and Weibull (1999). Gale and Rosenthal (1999 ) reported a game between an "experimenter" and a representative or average "imitator" but the analysis remains that of a two-person game. Only Brusco (1999) reports a three-person game. Other papers concern replicator dynamics in which every agent in a population of n agents plays one other agent. Each agent has a strategy and the strategies of the winning agents increase as a proportion of the population which remains at size n. The replicator dynamic models were reported by Alós-Ferrer ( 1999), by Sáez-Martí and Weibull ( 1999) and by Jackson and Kalai (1999).

n-player games

5.4

Among the n -player game theoretic models, Chakrabarty's is actually dynamic in the sense that all players play all other players at a sequence of time steps (Chakrabarti, 1999). This differs from models of self organised criticality in that every play has a fixed set of behaviours and, given current behaviour, a probability of changing at the next time step to each of the behaviours in the set. These probabilities of course sum to unity - else they would not be probabilities. Consequently, the agents are not metastable in the sense that some pressure builds until a threshold is reached to force change and the impetus to change is not a result of the behaviour of other agents. The model is constructed so that the distribution of the scale of changes cannot have the fat tail of the power law distribution. In effect, the possibility of producing the statistical signature of real markets is assumed away by the adoption of a Markov transition matrix.

5.5

One paper, Dekel and Scotchmer, 1999, reports a model with replicator dynamics in which more than two players are matched in each game, but the players' decisions are constrained by a Markov process which, again, prevents the emergence of a power law distribution.

5.6

The remaining papers do not relate to dynamic processes at all. Chakravorti, 1999, for example, reports theorems on equilibrium states. Bergin and Duggan, 1999 assert, "The central problem of mechanism design, an unavoidable consequence of the planner's incomplete information, is to ensure that socially desirable outcomes are achieved by a fixed mechanism as individual preferences are allowed to vary over some predetermined domain." Without pausing to enquire as to why restricting individual preferences is part of "the central problem of mechanism design", it is simply noted here that none of the results reported by Bergin and Duggan, 1999 are about mechanism as process. Every result is the solution of a game. This is entirely reminiscent the traffic equilibrium in which every car is travelling at the maximum speed. The traffic equilibrium is extremely unstable and there is no mechanism to bring the system towards that equilibrium. No results on dynamic stability were offered by Bergin and Duggan or, indeed, by the authors of any of the other papers on equilibrium game solutions.

5.7

Another discussion of "mechanism" is offered by Saijo and Yamato, 1999 who define a two-stage game. "In the first stage, each agent simultaneously decides whether she participates in the mechanism or not. In the second stage, knowing the other agent's participation decision, the agents who selected participation in the first stage choose their strategies." (p. 231) The mechanism is in fact an equilibrium outcome. The choice of whether to participate in the mechanism - to accept the equilibrium outcome - is determined for each agent by the maximisation of a utility function of consumption of one private and one public good. The simultaneity of the first stage decision ensures that there is no interaction among the agents. Consequently, we again find that the conditions that lead to self organised criticality and hence to the statistical signature of criticality are excluded by the assumptions of the model.

5.8

Cozzi's model of cooperation in R&D (Cozzi, 1999) excludes metastability by assuming consumers have perfect foresight with respect to the determinants of their consumption and considering only cases where firms are in a Nash equilibrium.

Summary

5.9

The assumptions of the game theoretic models published in the 1999 Journal of Economic Theory preclude the emergence of self organised criticality. The relevant common features of these models are the representations of behaviour as maximisation over continuous functions, thereby to preclude metastability and the adoption of assumptions that have the effect of precluding a dense network of interaction among the agents. As a result, agents cannot get into critical states because they are always in the state appropriate to the current state of their environment and the system is not self organising because changes in the behaviour of any one agent cannot induce cascades of changes in other agents. There is nothing analogous to the avalanche in any of these game theoretic models.

5.10

Of course there is nothing in this argument to prove that, in principle, game theoretic models cannot produce power law distributions in conditions where these are observed in reality. While self organised criticality implies power law distributions, there is no reason to believe that power law distributions imply self organised criticality. If the game theory research community is concerned with the validation of their models, members of that community might wish to demonstrate that game theory can be used to generate outputs with statistical signatures found in the real world. It is not for those of us who find the common assumptions of game theory to be implausible to attempt such a partial validation of that theory.

Conclusion

6.1

The purpose of this paper has been, first, to demonstrate that social simulation models devised to represent and analyse observed social phenomena produce data with statistical signatures of a sort found in the real world and, second, to explain why the only known mechanism found reliably to produce that statistical signature is precluded from consideration by the assumptions on which state-of-the-art game theoretic models are built. The history of the development of the model of market intermediation and the development of game theory indicate that both results follow naturally from their research programmes.

6.2

The model reported here is an extension of that reported by Moss (Moss, 2000a) and, more extensively, by Moss (http://www.cpm.mmu.ac.uk/cpmrep51 ). That model was developed to test specific properties of a historical analysis of the technology of exchange and how changes in technology influence the institutional fabric of exchange. The particular proposition being formalised and tested with that model was that intermediation is feasible if and only if the costs incurred by the intermediary are less that the cost savings realised by the intermediaries' customers and suppliers. This in turn requires the intermediaries to achieve economies of scale in exchange that are not available to their customers and suppliers.

6.3

The first model verified this proposition in an environment in which every agent could communicate with every other agent. The model reported here extended that model by restricting direct communication among agents to a set of "neighbours". The result was to confirm the initial proposition and results of the first model as a necessary condition for the feasibility of intermediation. A further necessary condition is that there be some critical size and density of the population of agents.

6.4

The literature on the power law distribution was unknown to me when developing these models. When I did become aware of it, I tested for the power law distribution of market shares with the results reported in section 3. I then sought further confirmation that market shares are power law distributed in the real world - with the results reported in section 2.

6.5

The literature on self organised criticality also came to my attention after the models were built and then because of following up the literature on power law distributions.

6.6

The important point here is that the model mechanisms were built to investigate specific historical, social phenomena. The specification of agents was suggested by the literature on cognitive science - the Soar and ACTR projects. The emergence of self organised criticality and the power law distribution amounts to a correct scientific prediction.

6.7

Consider now by way of contrast the history of the development of game theory. Economics has never been able to accommodate in analytical models the consequences of interaction among dense networks of agents. The inventor of general equilibrium theory, Leon Walras, invented a fictional process of tâtonnement whereby all agents would post their demands and supplies for all goods with an auctioneer who would call out prices intended at each round to bring the supplies and demands into equality. Trades would only take place once all supplies and demands were equal. The agents did not communicate directly with one another - a fiction that certainly had the effect of eliminating the kind of agent interaction which, had the agents been metastable, would have made self organised criticality feasible. The inventor of partial equilibrium analysis, Alfred Marshall, developed the concept of the representative firm because he could not handle the mathematics of interaction among many heterogeneous agents. He also argued that this should be a temporary step abandoned as soon as possible.

6.8

The result has been the application of representative agents to general equilibrium theory and the justification of replicator dynamics by appeal to the lack of reality of the process of tâtonnement. In the words of Binmore, Piccione and Samuelson (Binmore, 1997), "we treat the ... game as a metaphor for an evolutionary process in much the same way that the auctioneer of neoclassical economics is a metaphor for some unmodeled process that eventually equates supply and demand." Economics has cut its theoretical coat to suit the cloth of its analytical technique.

6.9

It is ironic that game theory was invented by von Neumann and Morgenstern to enable economists to analyse interaction among agents. This early post-war development was a response to the pre-war development of monopolistic competition theory in which it is assumed that the behaviour of each firm affects the demands faced by every other firm and that every firm recognises those effects. The effects were assumed to be spread across all firms so that, if the number of firms were sufficiently large, the effect on any one firm of the actions of any other firm would be negligible. But if the number of firms is small the effects are not negligible and game theory is relevant in those circumstances where each firm can identify the other firms whose actions are affecting its own profits.

6.10

The evidence from the 1999 Journal of Economic Theory papers is that, in more than half a century since the publication of von Neumann-Morgenstern (1947), no significant progress has been made in the development of models that captures the process of interaction among more than two or three agents.

6.11

The immediate precursor of the model reported here (Moss, 2000a) was developed to demonstrate that the assumption that agents maximise utility or profits severely restricts the scalability of models and multi agent systems more generally. The present model extends that result. This demonstration, together with the analysis of the 1999 JET articles, suggests that, on grounds of tractability, the representation of agents as constrained maximising algorithms restricts the density of the network of agent interactions. The simulation of metastable agents demonstrably does not prevent the density of interaction essential for self organised criticality and therefore the sorts of power law distributions observed in the real world.

6.12

I conclude therefore with the conjecture that no model of intermediated exchange in which agents are represented as constrained optimisers will ever yield a power law distribution of market shares as a robust result that is as insensitive to initial conditions and agent specifications as is the model reported in this paper.

Acknowledgements

The literature on power law distributions and self organised critical systems was brought to my attention by my colleague, Bruce Edmonds. My appreciation of their importance has resulted from long discussions with him. That power law distributions have no defined variance was pointed out to me by Rob Axtell of the Brookings Institution. Axtell also suggested to me the importance for my argument of the assumption in game theory that each agent is in a stable (rather than a meta stable) equilibrium. An earlier and much different version of this paper was read at the Montpelier workshop on game theory and agent based social simulation organised by François Bousquet. The lively discussion at that workshop helped to hone my arguments. I am particularly grateful to Jim Doran of the University of Essex who pointed out errant nonsense in the workshop paper. The model reported here was implemented in SDML, the strictly declarative modelling language produced by Steve Wallis in the Centre for Policy Modelling. SDML is developed and implemented in VisualWorks 5i produced and maintained by CinCom, Inc. We gratefully acknowledge our sponsorship arrangement with CinCom, Inc. who provide VisualWorks and permit us to distribute their object engine free of charge with SDML for use in academic research.

Appendix: 1999 Journal of Economic Theory articles on game theory

ALÓS-FERRER C. (1999) "Dynamical Systems with a Continuum of Randomly Matched Agents", Journal of Economic Theory 86(2), pp. 245-267

BATTIGALLI P., Siniscalchi M. (1999), "Hierarchies of Conditional Beliefs and Interactive Epistemology in Dynamic Games", Journal of Economic Theory 88(1), pp. 188-230

BERGIN J., Duggan J. (1999), "An Implementation- Theoretic Approach to Non-cooperative Foundations", Journal of Economic Theory 86(1), pp. 50-76

BRUSCO S (1999), "Implementation with Extensive Form Games: One Round of Signaling Is Not Enough", Journal of Economic Theory 87(2), pp. 356- 378

CHAKRABARTI S.K. (1999), "Markov Equilibria in Discounted Stochastic Games", Journal of Economic Theory 85(2), pp. 294-327

CHAKRAVORTI B. (1999) "Far-Sightedness and the Voting Paradox", Journal of Economic Theory 84(2) pp. 216-226

COZZI G. (1999), "R&D Cooperation and Growth", Journal of Economic Theory 86(1), pp. 17-49

DEKEL E., Scotchmer S. (1999). "On the Evolution of Attitudes towards Risk in Winner-Take-All Games", Journal of Economic Theory 87(1), pp. 125-143

GALE D., Rosenthal R.W. (1999), "Experimentation, Imitation, and Stochastic Stability", Journal of Economic Theory 84(1) pp. 1-40

JACKSON M.O., Kalai E. (1999), "Reputation versus Social Learning", Journal of Economic Theory 88(1), pp. 40-59

SÁEZ-MARTÍ M., Weibull J.W. (1999), "Clever Agents in Young's Evolutionary Bargaining Model", Journal of Economic Theory 86(2), pp. 268-279

SAIJO T., Yamato T (1999) "A Voluntary Participation Game with a Non-excludable Public Good", Journal of Economic Theory 84(2), pp. 227-242

STAMLAND T. (1999), "Partially Informative Signaling", Journal of Economic Theory 89(1), pp. 148-161

WALLNER K (1999) "Sequential Moves and Tacit Collusion: Reaction-Function Cycles in a Finite Pricing Duopoly", Journal of Economic Theory 84(2), pp. 251-267

References

ANDERSON,J.R. (1993) Rules of the Mind. Lawrence Erlbaum Associates .

BAK, P. (1997) How Nature Works: The Science of Self Organized Criticality. Oxford, Oxford University Press.

BINMORE,K. M. Piccione and L. Samuelson (1997) "Bargaining Between Automata" in Rosaria Conte, Rainer Hegselmann and Pietro Terna (eds), Simulating Social Phenomena (Berlin: Springer-Verlag, Lecture Notes in Economics and Mathematical Systems), pp. 113-132.

COHEN,Paul R. (1985) Heuristic Reasoning: An Artificial Intelligence Approach. Pitman .

JENSEN, H. (1998) Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems. Cambridge: Cambridge University Press.

LAIRD, J.E., A. Newell and P.S. Rosenbloom (1987) Soar: An Architecture for General Intelligence. Artificial Intelligence, 33: 1-64.

MOSS, Scott, Helen Gaylard, Steve Wallis and Bruce Edmonds (1996) SDML: A Multi-Agent Language for Organizational Modelling. Computational and Mathematical Organization Theory, 4: 43-69.

MOSS, Scott. (1998) Critical Incident Management: An Empirically Derived Computational Model. Journal of Artificial Societies and Social Simulation, 1 (4), <http://www.soc.surrey.ac.uk/jasss/1/4/1.html> .

MOSS, Scott. (2000a) Applications-Centred Multi Agent Systems Design with Special Reference to Markets and Rational Agency. In Proceedings of the 4th International Conference on Multi Agent Systems.

MOSS, Scott. (2000b) Canonical Tasks, Environments and Models for Social Simulation. Computational and Mathematical Organization Theory, 6: 249-275.

NAGEL, K. and M. Paczuski (1995) 'Emergent Traffic Jams', Physical Review E 51(4), pp. 2909-2918

NEILSEN (1992) The Retail Pocket Book 1993. Henley-on-Thames: NTC Publications Ltd..

von NEUMANN, J. and O. Morgenstern (1947) Theory of Games and Economic Behaviour. Princeton: Princeton Unversity Press, 2nd ed.

PARETO, Vilfredo (1896) Cours d'economie politique. Lausanne.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, 2001