© Copyright JASSS


Warren Thorngate (2000)
Teaching Social Simulation with Matlab
Journal of Artificial Societies and Social Simulation
vol. 3, no. 1,
<https://www.jasss.org/3/1/forum/1.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 16-Dec-99
Accepted: 25-Jan-00
Published: 31-Jan-00
 Abstract
Abstract
-
Programming languages for social simulations are rapidly proliferating.
The result is a Tower of Babel effect: Many of us find it increasingly effortful
to learn and to teach more programming languages and increasingly difficult
to sustain an audience beyond the programming dialect of our choice. We need
a programming lingua franca. Here I argue why Matlab might be worth our consideration, especially to teach simulation programming techniques.
- Keywords:
-
Simulation, teaching, social processes, programming languages, Matlab
 Introduction
Introduction
- 1.1
- When I wrote my first computer simulations in the late-1970s (Thorngate,
1980) there were few programming languages to choose. Beyond the acronymic
FORTRAN, BASIC, COBOL and ALGOL were the so-called "research" languages
such as SNOBOL, LISP and FORTH. All had their strengths and weakness. But
none of them had elegant ways of manipulating the rows and columns and cells
of matrices that represented the crux of my simulations -- manipulations that
are now common in social simulations. I thus resigned myself to mastering
the iterative art of the nested loop.
- 1.2
- Then I discovered APL. Kenneth Iverson, its developer, had modestly named
it "a programming language", but it was certainly not just another
one. Here was a language that did for matrices what Arabic numbers did for
roman numerals. A single line of code could give me a three-dimensional matrix
of random numbers; a single expression could find the largest of these numbers,
another could find their sum, and another could rotate rows or columns around
their axes. APL was an interpreter, so I could discover my syntactical sins
each time I pressed the Return key. APL even saved my data in the same file
as my programme, so I didn't even need to remember two file names.
- 1.3
- Alas, APL also had its flaws. Chief among them was its availability (the
language was owned by IBM and originally available only on its mainframes)
but so too was its alphabet. APL defined matrix operators with symbols inspired
by the Greeks, and it required a special keyboard and monitor to use. I suspect
IBM hoped it would sell lots of new keyboards and monitors this way, and maybe
it did. But by the time personal computers had infiltrated academic offices,
APL had drifted into graveyard of Obscure Languages, pushed out by a succession
of linguistic fashions such as Pascal, Smalltalk, c, c++, Prolog, Visual Basic
and Java, never to be taught in university again.
- 1.4
- Astonishingly, these newer and more fashionable languages retained the same
matrix limitations of the old. Curly brackets replaced the words "for",
"next", "begin" and "end", but a loop by any
other name remained the same, and once again those of us with matrices to
manipulate faced repetitive strain injuries from an overused Tab key. I am
not sure why. Perhaps in their rush to objects, the developers of these languages
forgot to ask social scientists what kind of functions we wanted built-in.
Perhaps the developers thought of us as sissies, like those who want an automatic
in a stick-shift programming world.
- 1.5
- For my fortunate simulation colleagues a solution was at hand. During the
time I left the world of simulation for a twelve year hiatus in the Third
World, many of them were benefiting from the greatest scientific invention
of the 20th Century: the research grant. My grant-rich colleagues had money
to pay programmers who worried about the loops and money to attended conferences
to show the results. My grantless colleagues became involved in teaching,
as did I. Alas, few of us taught computer simulation because we didn't know
how to teach it and didn't have time to learn. Those who mastered some programming
skills faced a more daunting challenge: teaching the skills to students more
interested in why societies form or change than in how to redimension a variable
or clear a stack. Judging from my own experience, most social science students
find computer programming to be, like opera, an unnatural act -- one as mystifying
to them as social science is to students of computer programming. So perhaps
it is not surprising that computer simulation has not yet captured the attention
or imagination of many social science students.
- 1.6
- What to do? If we want more students to learn how to write and evaluate
computer simulations, then an obvious possibility is to develop another programming
language which offers features social simulators desire but which is more
accessible, easier to teach and to use. Judging from my perusal of the recent
social simulation literature, the desirable features include speed, programming
simplicity, commands for manipulating lists, vectors and matrices, commands
for random sampling and shuffling, commands for creating, linking and modifying
"agents" (aka "objects"), commands for fancy graphics
and for statistical analyses. Parts of this wish-list have inspired the development
of many new languages, so many that we may soon run out of four letter acronyms,
among them: SDML, ARVA, VIVA, LOGO, STAR-LOGO, Icon, Nial, BLUE, Green, Hope,
Dylan, Eiffel, Elf, ABC, Oberon, MIMOSE, MUMPS, Gauss, Smalltalk, Simpack,
Theta, Lingo and Z. Even APL was replaced by a more accessible sequel called
J. Each of these new languages is wrapped in its own philosophy, justified
by the developer's assessment of what features simulators most need, and supported
by its own enthusiastic clique. Which begs the question: If each of these
languages is so good for us, why are there so many of them?
- 1.7
- Since returning to the world of simulation, I have tried many of these languages.
Some will not run on my PC. Some will not run on my Mac. Many are poorly supported.
Many are slow. Most do only a few things well. Only a few have good matrix
commands. And I have yet to find one with a good manual. I am probably too
impatient and finicky. No doubt one of these languages or its progeny will
eventually evolve and conquer, and in ten or twenty years the students of
our students will embrace it with at least as much enthusiasm our current
students now embrace statistical analysis packages.
- 1.8
- In the meantime, those of us who teach simulation are faced with a plethora
of evolving languages that are inconvenient and time-consuming to learn and
to teach, and that may not survive as the fittest. Should each of us invest
our time in a different simulation language, teach our favourite to our students
and perpetuate our acronymic clique in hopes that our language will conquer?
Not if we want to avoid a simulated Tower of Babel. Should we write our simulations
in our favourite language and package them as commodities to protect our students
from the frustrations of learning to programme? Yes, if we want to teach our
students how to point, click and say "Cool!" No, if we want our
students to learn the art of translating ideas into code.
- 1.9
- So I have continued to look for a temporary solution. I asked my colleagues
in cognitive science what they are using these days. Most often their answer
is LISP. Sure enough, LISP is great for lists and lists of lists, and for
recursing down the slopes of spanning trees. LISP-STAT adds to these strengths
features for doing math and statistical analyses on lists. It is a fine programme
and a good contender for something useful while waiting for our lingua franca.
So too is Starlogo, though it is written for Macintosh computers and the current
Java version for other computers is somewhat buggy and slow. Even J has its
charms, though its poetic syntax, like that of APL, makes it rather rather
difficult for the prosaic among us to learn and to use.
- 1.10
- My quest for a temporary programming solution took me as far afield as engineering.
It was there I discovered Matlab. Short
for Matrix Laboratory and designed specifically for vector and matrix calculations,
Matlab is probably used as widely in engineering as SPSS is used in social
science. It is a relatively inexpensive interpreter (about $100 US for the
student version), easy to obtain, available for all major operating systems
(Windows, Mac, Linux, etc.) and well supported by a good company, The Mathworks,
which first offered it in 1984. Matlab has almost as many matrix manipulation
features as APL and J, and is a lot easier to use. Once a programme for inverting
matrices, solving linear equations and such, Matlab has evolved to be a remarkably
general language, with set, list and string manipulation features, object
oriented programming features, and a terrific range of plotting and graphic
commands. It also has commands for creating Graphical User Interfaces (buttons,
scroll bars, etc.) and the ability to embed Matlab programmes in Microsoft
Word documents, though these features are awkward to use. The
Matlab website lists hundreds of Matlab programmes and about 300 Matlab
textbooks in many languages to supplement the rather sparse manual that comes
with the programme. For a few dozen dollars more, one can purchase any of
about 30 "toolboxes" that add functions for specialized areas such
as neural nets, fuzzy logic, and statistics.
- 1.11
- Impressed by Matlab, I chose it for teaching a few one-week social simulation
workshops in Poland and Iran, and for a 12-week graduate course at my home
university. Armed with one of Mathwork's generous classroom licenses, I could
legally install Matlab on a room-full of PCs and watch a room-full of social
science students bang away at lines of simulation code. Much to my pleasant
surprise, about half of the students became sufficiently proficient to generate
their own simple simulations after about 6 hours of instruction and modification
of other simple simulations. The other half gave up, lost interest or learned
that the best way to programme is to sit next to a programmer and challenge
her/him to make the simulation go. I don't know if a 50% success rate is good
or bad. A Deadly Sin leads me think it is probably better than the rate for
equivalent simulation workshops using most other programming languages, but
I am too lazy to run the comparison groups.
- 1.12
- Instead, I now invest my time trying to improve the teaching of social simulation
with Matlab. An immediate challenge is to learn how to translate different
kinds of simulations into Matlab functions and commands. There are more flavours
of social simulation than ice cream flavours in a franchise: Monte Carlo,
cellular, agent-based, genetic, mimetic, and plain-old dynamic systems simulations
are a few. Some of these flavours are easy to programme in Matlab; some are
not. More importantly, however, I have found that simple simulations in all
these flavours are sufficiently easy to programme in Matlab that students
can at least understand the gist of relations between concept and code before
they lose attention and interest, that is, in about one hour.
- 1.13
- My experience teaches me that the first hour of teaching simulation is critical.
If I cannot make students comfortable with writing a short simulation programme
in that time, I have probably lost them. So I now postpone a philosophical
introduction and general overview of computer simulation in order to involve
students immediately in a simple programming exercise. Choosing the right
exercise is obviously important; the topic should engage student interest
but be programmable in 6-10 lines. Equally important is the method of instruction.
I find it impractical to begin by asking students to type an existing programme
line-by-line then to run it, because the students type in ignorance and many
make typing errors. As a result, I run from student to student searching for
the typos while the other students become increasingly impatient. So I ask
them to "learn by watching" how I do it on my wall-projected computer
screen, then ask them to type the lines after they see the results.
- 1.14
- When I ask a class of university social science students "Who has ever
written a computer programme?", about 1 in 10 confesses. Most of the
confessed recall writing a programme in BASIC during a high school math class,
but do not recall enjoying the experience. Only a few boast of their secret
programming passions. I gather from these responses that almost all the students
are familiar with using computer programmes but unfamiliar with writing them.
They are rank abecedarians. So I must begin with fundamentals of programming.
Matlab allows us to teach these fundamentals in less than 60 seconds.
|
|
The fundamentals
|
What to do
|
|
| start Matlab |
choose Matlab from the Start/Programs button at the lower
left of a Windows screen |
| stop Matlab |
drag the mouse to the word Exit under the File menu and
lift finger off clicker |
| understand what a prompt is and how to find it |
go to (scroll if necessary) the bottom of the white window and look
for two "greater than" or "French close-quote"
signs
-a|
with a blinking bar just to their right
|
| reduce fear of making a mistake |
when the prompt is found, press the palm of either hand down in the
middle of the keyboard, then press the key marked Enter. Example:
-a vugbhiu768rt
??? Undefined function
or variable 'vugbhiu76rt'.
-a
|
|
Curiously, students seem to enjoy palming the keyboard to make a mistake,
and many repeat the exercise a few times. I think it teaches them that no
matter what the type, they cannot break Matlab. This is the intention of the
exercise.
- 1.15
- Matlab has over 500 commands. Fortunately, students need only learn about
20 of them to develop effective social simulations. Many of the unused commands
are related to controlling fine points of graphs or graphical user interface
objects. I have found that these can be ignored and probably should be because
they tend to divert a student's attention away from the conceptual issues
of a simulation.
- 1.16
- My next task is to show them how Matlab can be used as a fancy calculator.
So I ask them to type in a few lines [shown in boldface] similar to those
below, to press the Enter key at the end of each line, and to watch how Matlab
responds
|
|
-a56.3+21-6
ans =
71.3000
|
|
-a3.1*[2 5 -1
3]
ans =
6.2000 15.5000 -3.1000
9.3000
|
|
-asort([5 2 8
6 2.3 41.8 -6.78 -4])
ans =
Columns 1 through
7
-6.7800 -4.0000
2.0000 2.3000 5.0000 6.0000 8.0000
Column 8
41.8000
|
|
-amean([5 2 8
6 2.3 41.8 -6.78 -4])
ans =
6.7900
|
|
-aceil(10*randn(3,5))
ans =
11 -8 8 9 -14
1 3 17 13 6
0 -13 -6 -15 -3
|
|
- 1.17
- The first example above rarely generates much student interest beyond noting
that Matlab prints "ans =" (short for answer) and the result of
the calculation as soon as the Enter key is pressed. The second example begins
to spark a bit of curiosity when students see that Matlab is smart enough
to assume that we want each of the four numbers separated by a space inside
the square brackets to multiplied by 3.1, and immediately gives us the answer
under the "ans=" line. The third and fourth examples show students
that Matlab has some commands (aka functions) with English names that do what
they say, in this case sorting the set of eight numbers within the square
brackets, and calculating the mean or average of the same set of eight numbers.
The fifth example demonstrates that not all Matlab commands are plain English
words, and that Matlab has its own grammar for doing calculations, in this
case for generating a 3x5 matrix of random numbers sampled from a normally
distributed population with mean = 0 and standard deviation = 1, for multiplying
each of the 15 numbers by 10, and for taking the next higher integer (ceil
= ceiling) of each. Matlab has a second random number command "rand"
which generates random numbers from 0 to 1 from a uniform distribution.
- 1.18
- The next important task is to teach the concept of a programme variable.
Students accustomed to the concept of a variable from high school algebra
are baffled by programming expressions such as X=X+1. To change their attitude,
I ask students to think of a programme variable as a label attached to a box
-- either a shoebox or an egg carton. I then ask students to understand that
the equal sign "=" is simply a one-symbol command that means "put
the result of what is on the right of the = sign into the box with the label
to the left of the = sign", noting that lines of programme are best read
from right to left, like Hebrew or Farsi. In Matlab, boxes can hold a single
number such as -64.71 or a row or column of numbers such as [-4.2 5.98 6.0
41.9504] or a series of rows and columns (a matrix of any number of dimensions).
When there is more than one number in a variable, call it eggbox, the first
number is referenced as box(1), the second as eggbox(2), etc. If eggbox were
a two dimensional matrix, the number in the third row, fourth column would
be referenced as eggbox(3,4). After a few minutes of practice with creating
such variables, most students understand the programming variable concept.
- 1.19
- Because so many social simulations make use of vectors and matrices, it
is important to teach students something about manipulating them. Below are
a few of the major vector and matrix manipulation commands.
|
|
In order to
|
Use the following command
|
Examples (omitting the >> prompt & extra
lines)
|
|
| Make a vector "vec"and a matrix "mat" |
[ ]
[ ] with semicolons to separate rows of a matrix
a function which returns a vector or matrix
|
vec=[34 65 - 61
0 5.934]
mat=[4 7 -3;-45
9 2.1;16 -2 16]
mat =
4 7 -3
-45 9 2.1
16 -2 16
mat=mod(round(10*rand(3,4)),3)
mat =
1 0 0 0
2 0 1 2
2 2 1 1
|
| make a vector or matrix with zero in each cell, or with
ones in each cell, or make a square matrix with ones down the main diagonal |
zeros, ones, eye |
vec=zeros(5,1)
vec =
0
0
0
0
0
mat=ones(2,3)
mat =
1 1 1
1 1 1
mat=eye(4)
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
|
| make a vector with consecutive numbers |
: (the colon) |
vec= 1:7
vec =
1 2 3 4 5 6 7
vec = 12:-3:1
vec =
12 9 6 3
|
| transpose a vector or matrix |
' (the apostrophe) |
vec=[5 3 7 1]
vec =
5 3 7 1
vec'
ans =
5
3
7
1
vec' * vec
ans =
25 15 35 5
15 9 21 3
35 21 49 7
5 3 7 1
mat=fix(10*rand(2,3))
mat =
3 8 4
5 9 1
mat'
ans =
3 5
8 9
4 1
|
| find the length, maximum, minimum, sum, mean, median,
variance, standard deviation of a vector |
length, size, max, min, sum, mean, median, var, std |
vec=[45 32 56 87
12 98 31 52]
vec =
45 32 56 87 12 98 31 52
length(vec)
ans =
8
max(vec)
ans =
98
min(vec)
ans =
12
sum(vec)
ans =
413
mean(vec)
ans =
51.6250
median(vec)
ans =
48.5
var(vec)
ans =
835.1250
std(vec)
ans =
28.8985
|
| find the size, column maximum, column mean, etc. of a
matrix |
size, max, mean,...
(NB the last example shows how to obtain the mean of the rows of
a matrix: first do a row-column transformation, the ask for the column
means)
|
mat=[6 9 1 0;4 4
11 6;9 31 5 3]
mat =
6 9 1 0
4 4 11 6
9 31 5 3
size(mat)
ans =
3 4
max(mat)
ans =
9 31 11 6
max(max(mat))
ans =
31
mean(mat)
ans =
6.333 14.667 5.333 3.000
mean(mat')
ans =
5.333 6.333 16.000
|
| extract parts of a vector or matrix |
: (colon) |
vec=[41 82 53 94
25 36 77]
vec =
41 82 53 94 25 36 77
part=vec([5 4 3])
part =
25 94 53
part=vec(3:6)
part =
53 94 25 36
mat=[11 12 13 14;21
22 23 24;31 32 33 34]
mat =
11 12 13 14
21 22 23 24
31 32 33 34
part=mat([3 2],[3
4])
part =
33 34
23 24
part=mat(:,4)
part =
14 24 34
part=mat(2,:)
part =
21 22 23 24
|
|
- 1.20
- I suppose everyone likes to see pictures, and simulation students are no
exception. After the few number exercises above, students appreciate a graphic
break with a few simple plotting exercises. Here are four:
|
|
Matlab commands...
|
and the resulting Figure
|
|
|
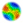
-a x=1:5
x =
1 2 3 4 5
-a y=[27 -13 98
-2 21]
y =
27 -13 98 -2 21
-a plot(x,y)
|
|
|
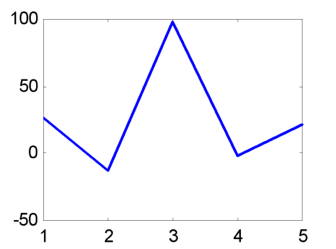
-a IQ=100+(15*randn(1,1000));
-a hist(IQ)
|
|
|
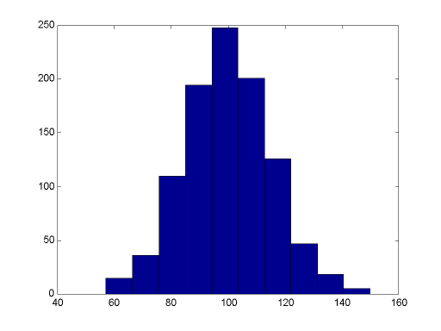
-a mymatrix=ceil(80*rand(8,8))
mymatrix =
59 55 72 43 27 65
68 77
34 5 61 5 39 49 37 52
77 29 64 8 48 57 77 20
6 40 66 22 13 8 12 29
45 35 54 33 67 34 70 16
24 45 17 38 77 31 62 40
69 50 22 73 48 14 36 33
27 10 51 48 3 67 50 38
-a image(mymatrix)
|
|
|
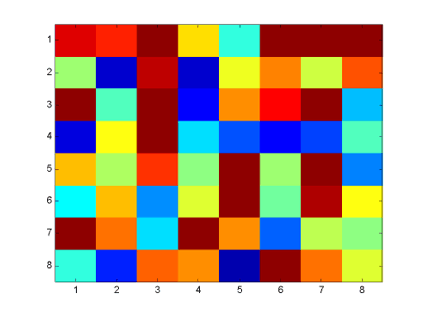
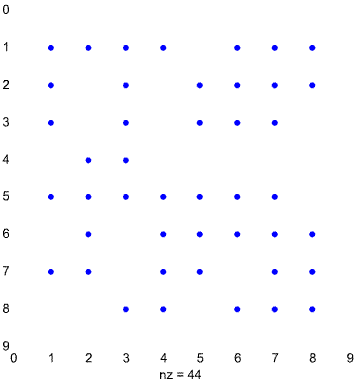
-a spy(mymatrix<30)
|
|
|
- 1.21
- The first exercise above shows students how to create two vectors, x and
y, and plot them on a graph. The variable y is defined as the five consecutive
numbers between square brackets, and the two variables are then plotted in
a line graph. The second exercise shows students how to generate a vector
of 1000 numbers sampled from a population with an average of 100 and a standard
deviation of 15, then display the vector in a histogram with 10 default categories.
The semi-colon at the end of the first line of this example shows can suppress
the output of Matlab. The third exercise shows how to create a crazy quilt
of colours based on the cell values values in a matrix, useful for watching
changes in cell values over time. The final exercise is a variation of the
third, showing how to manipulate a few Matlab commands to plot cells of a
matrix which satisfy some condition (in this case, mymatrix values less than
30) as blue dots, albeit rotated by 90 degrees.
- 1.22
- I have noted in teaching the material above that even though it is trivial
to those of us with some programming experience, it is a brain stretch for
the uninitiated, reminding me of Gary Larsen's wonderful Far Side cartoon
of the boy in the front of a class who asks to be excused because his brain
is full. After a short break, students return to watch, then try, the development
of their first simulation.
 Writing a simulation in Matlab: "Take it or leave it."
Writing a simulation in Matlab: "Take it or leave it."
- 2.1
- My simulation teaching experience teaches me there are five rules of engaging
students in their first simulation:
- keep it simple,
- keep it short,
- keep it interesting,
- teach it in small steps, and
- review often.
- 2.2
- Alas, the rules exclude lots of engaging simulations such as a game of life
or an ant colony because their programmes are too complex to teach students
as their first coding assignment. I have been searching for the pedagogically
simplest possible simulation for some time. My current choice is almost trivial,
but it can be written in seven lines of Matlab code and seems to pass the
student's "I Understand!" test more often than not. Like all good
simulations, this one begins with a story.
- 2.3
- I have spent many years studying the psychology of decision making, slowly
discovering the obvious: good or bad decisions are not always the result of
good or bad cognitions; they are equally often the result of good or bad circumstances
(e.g., see Thorngate, 1988; Thorngate & Carroll, 1987, 1991; Thorngate
& Hotta, 1995; Thorngate, Hotta & McClintock, 1996). Sometimes we
just can't win and sometimes we just can't lose despite our best or worst
decision processes. Thus our task in life is as much to find winning situations
and to avoid losing ones as it is to learn the best way to choose from the
alternatives given by the situations we are in.
- 2.4
- Different situations not only give us more or fewer, good or bad alternatives,
they also give us alternatives at different times. Supermarkets, for example,
present us with many alternative products at the same time, allowing us to
compare them at once before we choose which to buy. Other situations do not
give us this simultaneous luxury. Instead we must examine each alternative
one at a time and, to use the vernacular, "Take it or leave it."
When they are scarce, jobs, homes, scholarships and spouses are usually subject
to take it or leave it constraints. Few employers, for example, would keep
a job offer open for us several months while we looked for a better one.
- 2.5
- When circumstances face us with a take it or leave it decision, one of
the few ways we have to make the decision is to set some minimum standards
for what we want, then wait for each alternative to come, one-by-one, until
the first one appears that meets or exceeds our standards. We then choose
it. This decision process faces us with a dilemma: if we set our standards
low, we would probably make a quick decision but would also increase the chances
that a subsequent, perhaps the next, alternative would be better and that
we would regret our choice. In contrast, if we set our standards high, the
chances of regret would be lower but our patience might be stretched waiting
for Godot. What is the relationship between the height of our standards, the
distribution of alternatives and the number of alternatives we must reject
before the first acceptable one comes along? The present simulation is one
attempt to answer this question.
- 2.6
- To make the simulation a bit more concrete for students, I ask them to assume
that a friend is looking for a mate. The friend constructs a mental list of
desirable features in a mate: honesty, intelligence, beauty, good simulation
skills, etc. In our first simulation we are going to vary the number
of features on this list. We begin by assuming that the friend's list has
12 items. We then assume that prospective mates vary in the number of features
the friend wants; some of the prospects have none of the features, some have
only a few, some have most or all. We further assume that these features are
normally distributed. We can vary the parameters of the distribution, but
to begin we assume that the prospects have an average of 10 features and a
standard deviation of 3. Thus, to begin, the friend wants two more than the
average number of features. We begin the simulation by telling Matlab to give
us a string or vector of, say, random numbers sample from a population with
a mean of 10 and standard deviation of 3, each number representing the features
of a prospect:
|
| Matlab code and response |
Explanation |
|
|
prospects=ceil(10+3*randn(1,100))
prospects =
Columns 1 through 12
9 6 11 11 7 14 14 10 11 11 10 13
Columns 13 through
24 9 17 10 11 14 11 10 8 11 6 13 15
Columns 25 through 36
8 13 14 6 6 12 9 13 13 13 14 13
Columns 37 through 48
14 7 10 10 6 11 7 15 8 12 11 8
Columns 49 through 60
4 10 7 12 12 16 12 9 12 7 10 10
Columns 61 through 72
11 10 14 5 12 13 13 12 11 13 12 10
Columns 73 through 84
9 10 6 10 11 11 15 9 12 13 13 8
Columns 85 through 96
11 11 7 8 14 10 12 11 9 9 12 8
Columns 97 through 100
13 12 8 10
|
Generate a vector of 100 numbers (columns) sample from a normal distribution
with mean - 0 and standard deviation =1;
multiply each number by three;
add ten to each number;
then take the next higher integer (ceil) of each number
Results:
prospect(1) has 9 desirable features
prospect(2) has 6 desirable features
prospect(3) has 11 desirable features...
prospect(100) has 10 desirable features
|
|
- 2.7
- When teaching a room-full of students with computers running Matlab, it
is difficult to prevent them from typing in the same Matlab command: prospects=ceil(10+3*randn(1,100)).
So I encourage it. But it is important to remind the concrete thinkers among
the students that their 100 numbers will almost certainly not be the same
as those above because Matlab takes a different sample each time. Following
the reminder, I ask students to tell me how many prospects their friend must
examine or date before finding one that has the 12 features he/she wants.
Moving their fingers across the table/screen above, and sometimes moving their
lips, they count. In the example above, they note that a friend would need
to date 6 prospects before finding one who had at least 12 desirable features,
rejecting person 1 with 9 features, person 2 with 6 features, etc., until
they reached person 6 with 14 features. Then they count their own screen,
call out the answers and I write them on a chalkboard: 3, 11, 5, 2, 4, 2,
etc.
- 2.8
- Now is the time to show them that Matlab can do the counting for them by
using the "find" command, putting the result in a variable called,
say, "goodones" and looking at the first number in this variable
= the first prospect who meets or exceeds the friends minimum feature requirements:
|
| Matlab command and response |
Explanation |
|
|
goodones=find(prospects
>= 12)
goodones=
Columns 1 through 12
6 7 12 14 17 23 24 26 27 30 32 33
Columns 13 through 24
34 35 36 37 44 46 52 53 54 55 57 63 Columns 25 through 36
65 66 67 68 70 71 79 81 82 83 89 91 Columns 37 through 39
95 97 98
goodones(1)
ans =
6
|
find the index numbers (#) of the prospects who have 12 or more features
and put the result in a variable called "goodones"
Result:
goodones(1) = #6
goodones(2) = #7
goodones(3) = #12
...
goodones(39) = #98
|
|
- 2.9
- Next I ask students to type the three lines of the programme ten times,
but with semi-colons at the end of the first two lines to suppress output,
and to write down the "ans =" they get each time. If they do it
correctly, their resulting screen looks something like this:
|
| Doing the simulation by hand |
|
|
prospects=ceil(10+3*randn(1,100));
goodones=find(prospects
>= 12);
goodones(1)
ans =
3
prospects=ceil(10+3*randn(1,100));
goodones=find(prospects
>= 12);
goodones(1)
ans =
2
prospects=ceil(10+3*randn(1,100));
goodones=find(prospects
>= 12);
goodones(1)
ans =
5
prospects=ceil(10+3*randn(1,100));
goodones=find(prospects
>= 12);
goodones(1)
ans =
4
|
|
- 2.10
- Most students become bored with the repetition, which is a primary goal
of the exercise. Before addressing their boredom, however, I ask each student
to average their ten "ans =" numbers, and to call out their average
for all to hear. We then average their averages, and arrive at a number: about
2.7. What does it mean? After some coaxing, most students begin to understand
that it means if friends want 12 features in a mate from a world in which
prospects average 10 features with a standard deviation of 3, then friends
must date an average of 2.7 people before find a suitable mate.
- 2.11
- Exploiting the boredom created by the exercise, I reveal that we can tell
Matlab to repeat the three commands as many times as we want, remember the
results, and the average the results when done. We do this by writing the
three commands and a few more in file and telling Matlab to do the commands
in the file. The result will be the students first simulation programme. Most
students become anxious at this time. But we press on. We begin by using the
Matlab command "edit" which starts the Matlab editor. Then I write
the three lines and save them in a file called "takeit":
|
| Matlab command |
Explanation
|
| edit |
Start the Matlab editor |
prospects=ceil(10+3*randn(1,100));
goodones=find(prospects >= 12);
goodones(1) |
find all prospects with 12+ good features
generate the # of features for each prospect
show the 1st prospect to have 12+ good features
|
| ctl-s
(cmd-s for Matlab on a Mac) |
save the file, using the arbitrary name: takeit |
|
- 2.12
- Students do the same. When the file is saved, I ask them to return to the
regular Matlab window and type the six-letter word "takeit" followed
by the Enter key. Here is what they might see:
|
|
takeit
goodones(1) =
6
takeit
goodones(1) =
1
takeit
goodones(1) =
2
takeit
goodones(1) =
3
|
|
- 2.13
- The exercise demonstrates how a series of Matlab commands can be put in
a file, and how the name of the file becomes a new command in Matlab. Most
students are moderately impressed by this. We then type "edit takeit"
to add four new lines to the "takeit" file, two above the existing
three lines and two below them.
|
| Matlab command (N.B. Matlab's editor automatically indents
lines between for and end statements to make the programme
pretty) |
Explanation
|
|
| edit
takeit |
Start the Matlab editor |
result=zeros(1,1000);
for student=1:1000
prospects=ceil(10+3*randn(1,100));
goodones=find(prospects >= 12);
result(student)=goodones(1);
end
mean(result) |
initialize the count
for each of 1000 trials
start the 1000 trials
find all prospects with 12+ good features
generate the # of features for each prospect
record the 1st prospect to have 12+ good features
continue the loop of 1000 trials
now display the average of all 1000 trials
|
| ctl-s
(cmd-s for Matlab on a Mac) |
resave the file takeit |
|
- 2.14
- The next pedagogical challenge is to explain what these four new lines mean.
The top line makes a vector of 1,000 zeros. Each element will be used to hold
the result of one of a simulation done by one "student." The next
line sets up a loop of 1,000 iterations, each iteration representing one student
who does the simulation once. The fifth line puts the result (how many dates
before one with at least 12 desired features) into the the vector labelled
"result." The sixth line ends the loop, bringing Matlab back to
line three. And the last line calculates the average result across the 1,000
students (iterations). We resave the new version of the file with the ctl-s
command, and again type the six-letter neologism "takeit" in the
Matlab main window. After about one second, Matlab spits our the result: a
number hovering around 2.7.
- 2.15
- Students have just written and run their first simulation programme. Confidence
begins to grow. With luck, however, so will scepticism. While looking at the
"2.7" that Matlab spit on their screen, at least one student will
likely ask, "So what?" The question provides a good lead into a
modification of the programme which allows students to look at the relation
between the number of desired features and the average number of alternatives
to consider before finding the first acceptable one. Here is the modification
(shown in boldface), and the output when saved and run:
|
|
The modified programme (resaved with ctl-s)
|
|
|
numfeatures= input('How many desired features is your friend looking
for? ')
result=zeros(1,1000);
for student=1:1000
prospects=ceil(10+3*randn(1,100));
goodones=find(prospects >= numfeatures);
result(student)=goodones(1);
end
mean(result)
|
|
|
Running the modified programme
|
|
|
takeit
How many desired features is your friend looking for? 10
ans =
1.52
takeit
How many desired features is your friend looking for? 11
ans =
2.02
takeit
How many desired features is your friend looking for? 12
ans =
2.64
takeit
How many desired features is your friend looking for? 13
ans =
3.81
takeit
How many desired features is your friend looking for? 14
ans =
6.37
takeit
How many desired features is your friend looking for? 15
ans =
10.89
takeit
How many desired features is your friend looking for? 16
ans =
20.68
takeit
How many desired features is your friend looking for? 17
ans =
43.98
|
|
- 2.16
- To be honest, when students input anything above 15, they will probably
get an error message on the screen. This is because Matlab could not find
any "date" with at least 15 features in a random list of 100 it
generated. To fix this problem, students change the line
prospects=ceil(10+3*randn(1,100));
to
prospects=ceil(10+3*randn(1,1000));
increasing the number of prospects to 1,000. This allows students to
input numfeatures up to about 20.
- 2.17
- And what do students learn from this? I ask them to type the following from
the "runs" of the simulation they just completed:
|
|
x=10:17
x =
10 11 12 13 14 15 16 17
y=[1.52 2.02 2.64
3.81 6.37 10.89 20.68 43.98]
y =
1.52 2.02 2.64 3.81 6.37 10.89 20.68 43.98
plot(x,y)

|
|
- 2.18
-
QED: as the number of desired features goes up linearly,
the average number of alternatives that must be rejected before finding
an acceptable one goes up exponentially. If friends want an average number
of features in a mate, then they must date between one and two people before
finding an acceptable mate. If friends hold out for one standard deviation
above the mean, then they must date an average of 3.8 people. If friends
hold out for two standard deviations about the mean, then they must date
an average of 21.7 people. Three standard deviations will force them to
date hundreds. In summary, though it is noble to keep high standards, there
is an exponentially rising cost for doing so. When standards are quite high,
one might never find an acceptable alternative. There is thus truth in the
popular aphorism:
|
When all else fails, lower your standards.
|
 More advanced simulations in Matlab
More advanced simulations in Matlab
- 3.1
- The simulation above does not claim to be profound. Indeed, it is not even
social. The results simply demonstrate a statistical theorem. Yet I think
it has pedagogical worth, simply because it allows students to experience
the development of a successful simulation programme that leads to a philosophical
conclusion in less than an hour. If all goes well, students will soon want
to write programmes for cellular automata, agents and the like. If the simulations
involve "checkerboards", the matrix features of Matlab can easily
accommodate them. Consider, for example, how Matlab can calculate the number
of 1s in the four adjacent north, south, east and west cells of a 0/1 matrix,
assuming the edges of the matrix wrap around. This is, of course, a common
function for cellular automata simulations such as the Game of Life:
|
|
The Matlab function "neighbours" (entered
in Matlab's editor and saved as a file)
|
|
function result =
neighbours(x)
north=[x(2:end,:);x(1,:)];
south=[x(end,:);x(1:end-1,:)];
east=[x(:,end) x(:,1:end-1)];
west=[x(:,2:end) x(:,1)];
result=north+south+east+west; |
|
|
Using the "neighbours" function to calculate
the number of North, South, East and West
neighbours in each cell of a matrix called "bugs", assuming
rows and columns wrap around in torus fashion
|
|
|
bugs=rand(5,4)>0.5
bugs=
1 0 0 0
1 0 1 0
1 1 0 0
0 1 0 1
1 0 1 1
neighbours(bugs)
ans =
2 1 2 2
2 3 0 2
2 2 2 2
4 1 3 1
2 3 1 3
|
|
- 3.2
- Beginning with version 5.0 Matlab (now in version 5.3) added two useful
data types for agent-based simulation: cell and structure. They
are illustrated below:
|
|
Examples of a Matlab data cell
|
|
-a
dc(1,1)={rand(3,3)}
dc =
[3x3 double]
-a dc(1,2)={'hello there'}
dc =
[3x3 double] 'hello there'
-a dc(2,1)={[54 23 76]}
dc =
[3x3 double] 'hello there'
[1x3 double] []
-a dc(2,2)={-999}
dc =
[3x3 double] 'hello there'
[1x3 double] [ -999]
|
-a dc{1,1}
ans =
0.4235 0.4329 0.7604
0.5155 0.2259 0.5298
0.3340 0.5798 0.6405
-a dc{1,1}*dc{2,2}
ans =
-423.0728 -432.4737 -759.6046
-514.9962 -225.7239 -529.2933
-333.6175 -579.2271 -639.8860
|
|
|
Examples of a Matlab data structure
|
|
-a agent(1).name='mary'
agent =
name: Mary
-a agent(2)Name='fred'
agent =
1x2 struct array with fields:
name
-a agent(1).height=150
agent =
1x2 struct array with fields:
name
height
-a agent(2)Height=180;
-a agent(1).grades=[78 83 81];
-a agent(2)Grades=[66 61 75];
-a agent(1)Grades=[agent(1)Grades 89]; |
-a agent(1)Grades
ans =
78 83 81 89
-a agent(2)Grades=[agent(2)Grades 76];
-a agent(2)Grades
ans =
66 61 75 76
agent.name
ans =
Mary
ans =
Fred
-a sum([agent.grades])
ans =
531
mean([agent.height])
ans =
165 |
|
- 3.3
- I should note that Matlab also has capabilities for constructing classes
and objects, and for inheritance and overloading, that should appeal to object
oriented programmers. It also has facilities for handling sparse matrices
(matrices with lots of empty cells) that conserve large amount of memory.
Like LISP, it also has an "eval" function to evaluate a string variable
as a Matlab command line, and an "feval" function to evaluate a
string variable that names a function. Matlab has a few string functions,
but nothing as nice as those in, say, Icon or Tcl/Tk. The few graphs I show
above do not do justice to Matlab's graphing capabilities; better examples
can be seen at the Matlab website. Matlab
even has the capability to animate graphs and, as noted previously, to create
graphical user interfaces which make for slick push-button simulation products.
These facilities are, however, best for teaching what a simulation does, rather
than for teaching how to do one.
 Matlab variations
Matlab variations
- 4.1
- The popularity of Matlab in engineering and elsewhere has stimulated several
companies to develop Matlab variations. Mathviews is close to a clone
of Matlab, version 4. It does not have the fancy graphics features of Matlab,
only simple graphs, and it does not have any of its new data types. But it
is small (about 4 Mb on your hard disk versus 80+ Mb for the latest Matlab),
and the student version is free for the download (so too is the full version
if you can convince its developer that you are a professor). See the Mathwizards
website http://www.mathwizards.com
for more information. Mathviews is a wonderful way to introduce yourself to
the basics of a Matlab-like language for no cost (Matlab does not have a free
demo version).
- 4.2
- O'Matrix is a second "Matlab-like" programme which has
its own programming language similar in spirit to the Matlab language. The
latest version of O'Matrix (5.0) includes a feature that allows the user to
switch between the O'Matrix language or the Matlab language, giving it more
Matlab compatibility. O'Matrix claims to be far faster in execution than Matlab,
but my tests with its demo version indicate that it is slower on the kinds
of programmes discussed above. It is also more sparse, with more limited graphics
features than those in Matlab. The academic version is $95 US, about the same
price as Matlab's student version. For more information about O'Matrix go
to http://www.omatrix.com/
- 4.3
- Perhaps the most ambitious public
domain effort to develop a Matlab-inspired matrix language comes from France.
Scilab is a large programme (about 40 Mb) almost as rich in features
as is Matlab. Its graphics are very good, far superior to those of Mathviews
and O'Matrix. And, thank you INRIA, it is free. As with O'Matrix, however,
its programming language is similar in spirit but not compatible with the
Matlab programming language. For example, to generate a 3×4 matrix of random
numbers in Matlab, sampled from a normal distribution, we would type: x=randn(3,4).
In Scilab we would type: x=rand(3,4,'normal'). With comments in the code,
however, both are understandable. Scilab is definitely worth a download at
http://www.scilab.org/products/scilab
- 4.4
- The rlab programming language is another Matlab variant with its
own programming syntax. It has been written primarily for Unix machines, but
has a DOS version that runs under Windows. It is free and worth a try. But
it did not install easily on my NT machine or on my 98 machine, and seemed
to start with missing parts. I could find no graphics commands in rlab. Rlab
has a wonderful random number generator that emulates several distributions
(uniform, normal, Poisson, Beta, etc.) which I would like to see in Matlab
(where they are emulated in a pay-more, add-on statistics package). For more
information see the rlab web site, run by its developer Ian Searle, at http://www.eskimo.com/~ians/rlab.html
- 4.5
- If you talk to economists about simulation they will often mention GAUSS.
I have tried to learn more about GAUSS from the website of its developer,
Aptech Systems: http://www.aptech.com
Alas, the website is not very instructive. I once wrote to the company for
a listing of academic prices and found them rather steep (over $500 as I recall).
- 4.6
- A company called MathTools offers what appears to be a Matlab clone called
MIDEVA which the company claims will run Matlab programmes faster that
Matlab when filtered through a c++ compiler. Alas, one must buy a c++ compiler
separately, adding another $100 US or more to the cost of MEDIVA. More information
can be found at the MathTools website: http://www.mathtools.com
- 4.7
- As noted previously, Kenneth Iverson and colleagues developed a standard-keyboard
variant of APL called J which has many of Matlab's features and some
good graphics. However, its syntax remains rather obscure. For example, to
generate a 4x4 matrix, m, of random numbers that range from 0 to 9,
we would type: m=: ?. 4 4 $ 9. For more information, see the J website
at http://www.jsoftware.com A trial
version of J is available for download free of charge. A variation of J called
NIAL is also available free of change at the NIAL website: http://www.nial.com
- 4.8
- Two famous mathematics programmes, Mathematica and Maple,
have competed with each other in the equation solving and graphics market
for many years. Mathematica is a fancy programme and expensive (about $150
US for the student version and professor must buy the $400+ version). Maple
is a fancy programme and cheap (about $80 US for the student version). Both
have a wonderful facility for combining instructional text, "live"
equations and graphs into a single outline-style document, a pedagogical feature
sadly lacking in Matlab. Both have their own programming language that appears
less intuitive than the language of Matlab. And both have been slow and clumsy
at the numerical tasks for which Matlab is famous. Yet Mathematica now advertises
vector and matrix calculation features similar to Matlab in its latest version
(4), and Maple will offer its version 6 to the world in early 2000 with the
promise of similar features. For more information see the Mathematica website:
http://www.wolfram.com and the Maple
website: http://www.maplesoft.com
- 4.9
- It is well to remember that teachers and researchers, like artists and crafters,
should not fall in love with their tools. On the other hand, we should not
spend so much time learning to use tools that we have no time left to develop
ideas. Matlab allows students to get on with the business of developing and
testing social ideas in a reasonable amount time and with only moderate frustration.
It might not be all we want in a social simulation language, but my teaching
experiences lead me to conclude that, for now, Matlab is one of the best alternatives
we have.
 References
References
-
THORNGATE, W. (1980). Efficient decision heuristics. Behavioral Science, 25,
219-225.
THORNGATE, W. (1988). On the evolution of adjudicated contests and the principle
of invidious selection. Journal of Behavioral Decision Making, 1, 5-16.
THORNGATE, W. & Carroll, B. (1987). Why the best person rarely wins: Some embarrassing
facts about contests. Simulation and Games,18, 299-320.
THORNGATE, W., & Carroll, B. (1991). Tests versus contests: A theory of adjudication.
In Baker, W., Hyland, M., van Hezewijk, R., & Terwee, S. (Eds.), Recent trends
in theoretical psychology: Volume 2. New York: Springer-Verlag, pp. 431-438.
THORNGATE, W., & Hotta, M. (1995) Life and luck: Survival of the fattest. Simulation
and Gaming. 5-16.
THORNGATE, W., Hotta, M., & McClintock, C. (1996). Bingo! The case for cooperation
revisited. In Tolman, C., Cherry, F., & Van Hejiwek, R. & Lubek, I. (Eds.),
Problems of Theoretical Psychology. New York: Springer.

 Return to Contents of this issue
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1998
![]() Abstract
Abstract![]() Introduction
Introduction

![]() Writing a simulation in Matlab: "Take it or leave it."
Writing a simulation in Matlab: "Take it or leave it."
![]() More advanced simulations in Matlab
More advanced simulations in Matlab![]() Matlab variations
Matlab variations![]() References
References![]()
Return to Contents of this issue